期末闯关测试卷 (1) 上册-下册第二章(含答案) 2024-2025北师大版九年级数学上册
文档属性
| 名称 | 期末闯关测试卷 (1) 上册-下册第二章(含答案) 2024-2025北师大版九年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 266.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 15:59:03 | ||
图片预览


文档简介
期末测试卷
时间:90分钟 满分:120分 考试范围:上册全部~下册第二章
一、选择题(本题共10小题,每小题3分,共30分)
1.已知关于x的方程x2-mx-6=0的一个根为2,则m的值是 ( )
A.2 B.-2 C.1 D.-1
2.如图所示,该几何体的左视图是 ( )
A. B. C. D.
3.下列命题中,正确的是 ( )
A.菱形的对角线相等 B.矩形的对角线互相垂直
C.正方形的对角线相等且互相垂直 D.正方形的面积等于对角线的平方
4.在Rt△ABC中,∠C=90°,sin A=,那么sin B的值是 ( )
A. B.2 C. D.3
5.反比例函数y=的图象经过点(2,1),则下列说法错误的是 ( )
A.k=2 B.函数图象分布在第一、三象限
C.当x>0时,随x的增大而增大 D.当x>0时,y随x的增大而减小
6.如图,阳光透过窗户洒落在地面上,已知窗户AB高1.5 m,光亮区的顶端距离墙角3 m,光亮区的底端距离墙角1.2 m,则窗户的底端距离地面的高度(BC)为 ( )
A.1 m B.1.2 m C.1.5 m D.2.4 m
7.若关于x的方程x2-mx+-=0有两个相等的实数根,则反比例函数y=(x>0)的图象在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8.从1,2,3,4四个数中随机选取两个不同的数,分别记为a,c,则二次函数y=ax2+4x+c的图象与x轴有两个不同交点的概率为 ( )
A. B. C. D.
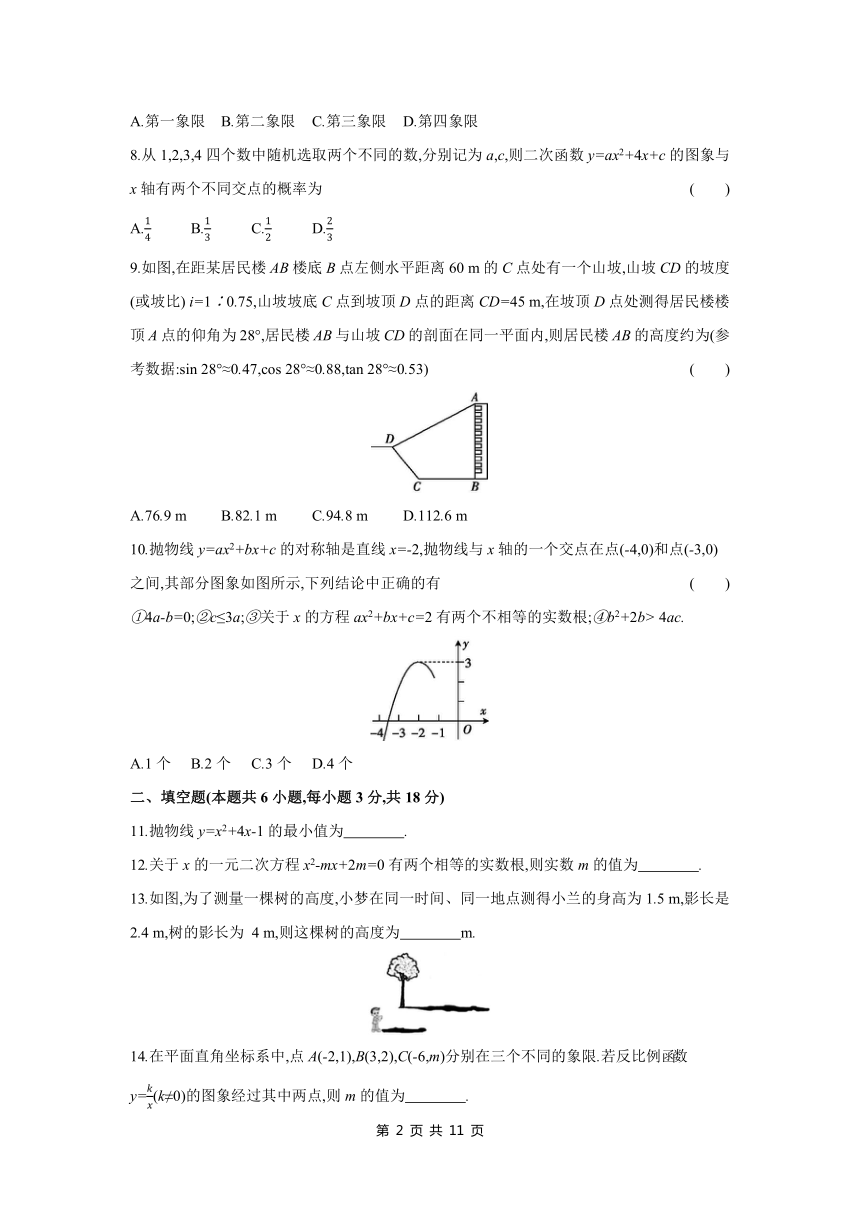
9.如图,在距某居民楼AB楼底B点左侧水平距离60 m的C点处有一个山坡,山坡CD的坡度(或坡比) i=1∶0.75,山坡坡底C点到坡顶D点的距离CD=45 m,在坡顶D点处测得居民楼楼顶A点的仰角为28°,居民楼AB与山坡CD的剖面在同一平面内,则居民楼AB的高度约为(参考数据:sin 28°≈0.47,cos 28°≈0.88,tan 28°≈0.53) ( )
A.76.9 m B.82.1 m C.94.8 m D.112.6 m
10.抛物线y=ax2+bx+c的对称轴是直线x=-2,抛物线与x轴的一个交点在点(-4,0)和点(-3,0)之间,其部分图象如图所示,下列结论中正确的有 ( )
①4a-b=0;②c≤3a;③关于x的方程ax2+bx+c=2有两个不相等的实数根;④b2+2b> 4ac.
A.1个 B.2个 C.3个 D.4个
二、填空题(本题共6小题,每小题3分,共18分)
11.抛物线y=x2+4x-1的最小值为 .
12.关于x的一元二次方程x2-mx+2m=0有两个相等的实数根,则实数m的值为 .
13.如图,为了测量一棵树的高度,小梦在同一时间、同一地点测得小兰的身高为1.5 m,影长是2.4 m,树的影长为 4 m,则这棵树的高度为 m.
14.在平面直角坐标系中,点A(-2,1),B(3,2),C(-6,m)分别在三个不同的象限.若反比例函数y=(k≠0)的图象经过其中两点,则m的值为 .
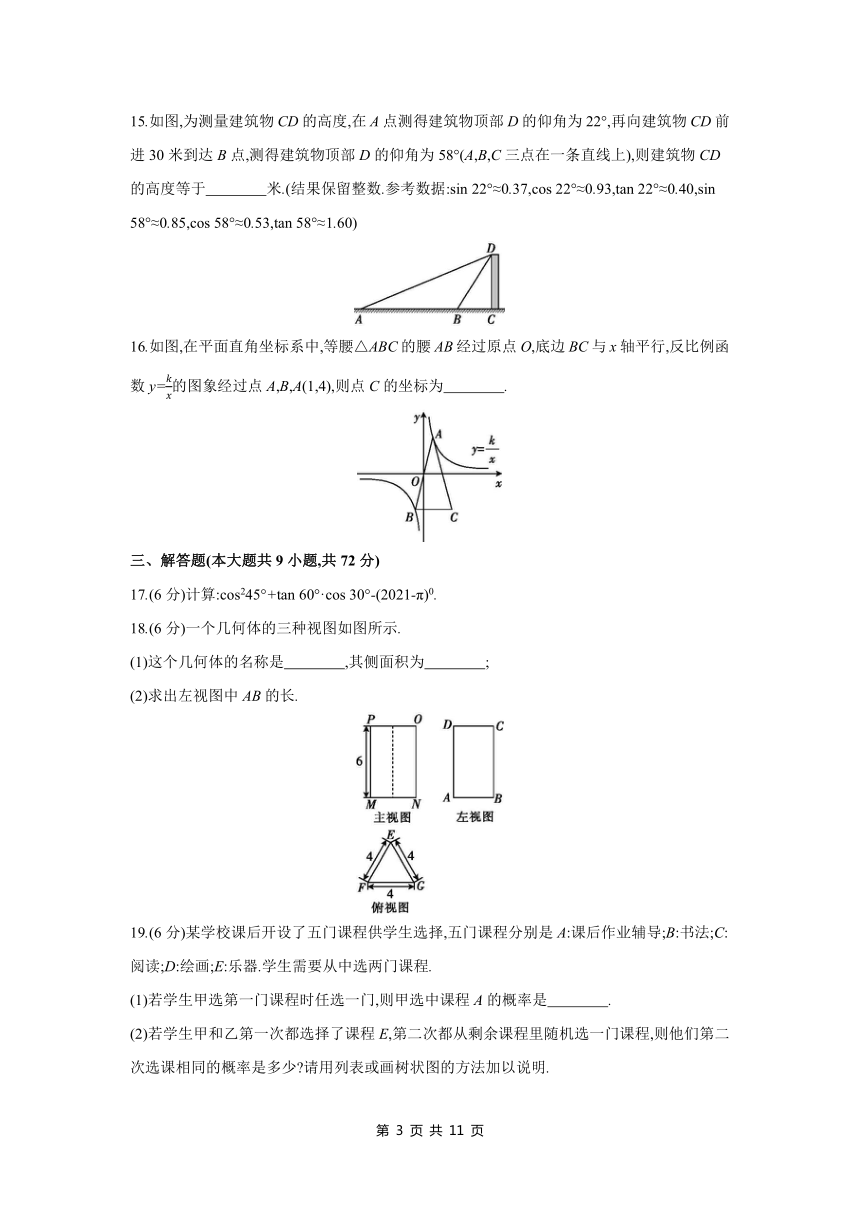
15.如图,为测量建筑物CD的高度,在A点测得建筑物顶部D的仰角为22°,再向建筑物CD前进30米到达B点,测得建筑物顶部D的仰角为58°(A,B,C三点在一条直线上),则建筑物CD的高度等于 米.(结果保留整数.参考数据:sin 22°≈0.37,cos 22°≈0.93,tan 22°≈0.40,sin 58°≈0.85,cos 58°≈0.53,tan 58°≈1.60)
16.如图,在平面直角坐标系中,等腰△ABC的腰AB经过原点O,底边BC与x轴平行,反比例函数y=的图象经过点A,B,A(1,4),则点C的坐标为 .
三、解答题(本大题共9小题,共72分)
17.(6分)计算:cos245°+tan 60°·cos 30°-(2021-π)0.
18.(6分)一个几何体的三种视图如图所示.
(1)这个几何体的名称是 ,其侧面积为 ;
(2)求出左视图中AB的长.
19.(6分)某学校课后开设了五门课程供学生选择,五门课程分别是A:课后作业辅导;B:书法;C:阅读;D:绘画;E:乐器.学生需要从中选两门课程.
(1)若学生甲选第一门课程时任选一门,则甲选中课程A的概率是 .
(2)若学生甲和乙第一次都选择了课程E,第二次都从剩余课程里随机选一门课程,则他们第二次选课相同的概率是多少 请用列表或画树状图的方法加以说明.
20.(6分)如图,在Rt△ABC中,∠BAC=90°,AB=9,AC=12,点D是斜边BC上的一个动点,过点D分别作DE⊥AB于点E,DF⊥AC于点F,点G是四边形DEAF的对角线的交点,求线段GF的最小值.
21.(8分)如图,在△ABC中,BC的垂直平分线分别交BC,AC于点D,E,BE交AD于点F,AB=AD.
(1)判断△FDB与△ABC是否相似,并说明理由.
(2)AF与DF相等吗 为什么
22.(8分)如图,在平面直角坐标系xOy中,反比例函数y=(x>0)的图象经过点A(4,),点B在y轴的负半轴上,AB交x轴于点C,C为线段AB的中点.
(1)m= ,点C 的坐标为 ;
(2)若点D为线段AB上的一个动点,过点D作DE∥y轴,交反比例函数的图象于点E,求△ODE面积的最大值.
23.(10分)小华同学将笔记本电脑水平放置在桌面上,当显示屏的边缘线OB与底板的边缘线OA所在水平线的夹角为120°时感觉最舒适(如图①),侧面示意图为图②;使用时为了散热,他在底板下面垫入散热架,如图③,点B,O,C在同一直线上,OA=OB=24 cm,BC⊥AC,∠OAC=30°.
(1)求OC的长;
(2)如图④,垫入散热架后,要使显示屏的边缘线OB'与水平线的夹角仍保持120°,求点B'到AC的距离.(结果保留根号)
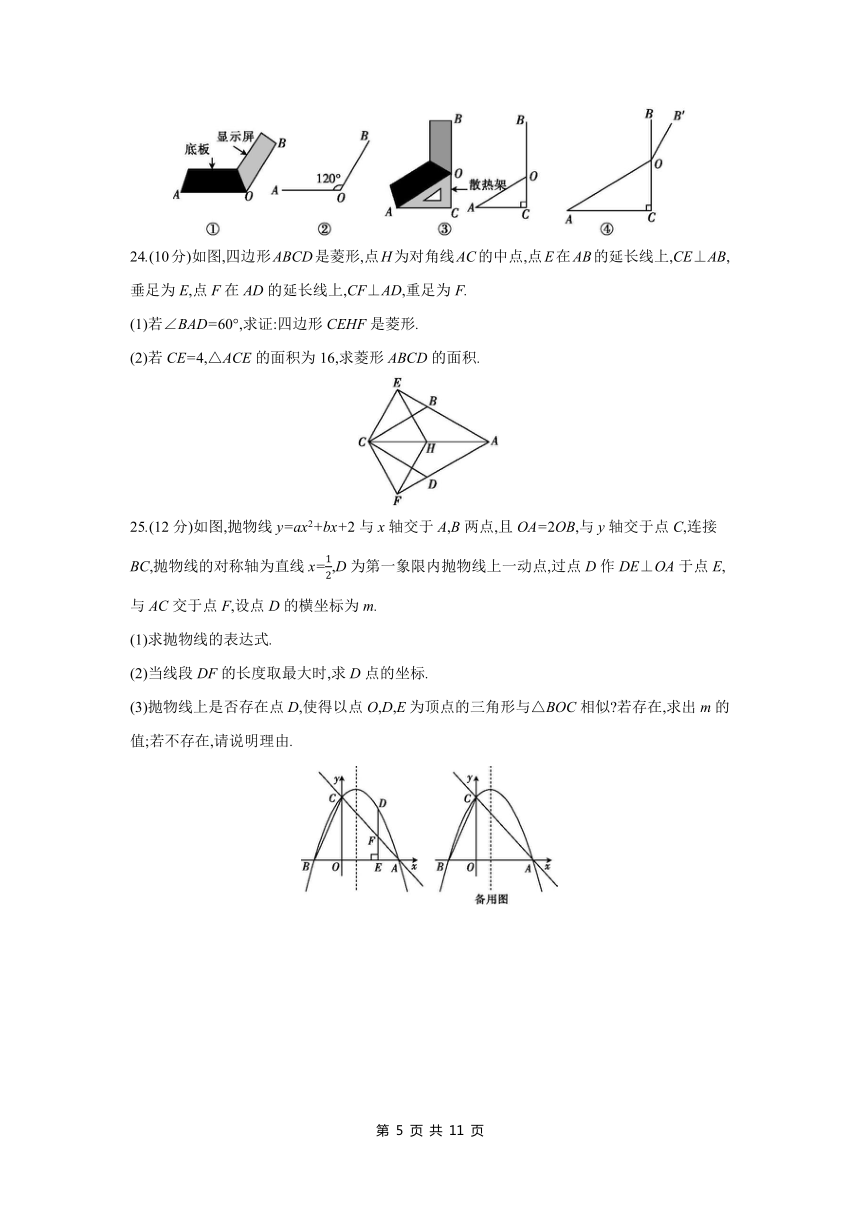
24.(10分)如图,四边形ABCD是菱形,点H为对角线AC的中点,点E在AB的延长线上,CE⊥AB,垂足为E,点F在AD的延长线上,CF⊥AD,重足为F.
(1)若∠BAD=60°,求证:四边形CEHF是菱形.
(2)若CE=4,△ACE的面积为16,求菱形ABCD的面积.
25.(12分)如图,抛物线y=ax2+bx+2与x轴交于A,B两点,且OA=2OB,与y轴交于点C,连接BC,抛物线的对称轴为直线x=,D为第一象限内抛物线上一动点,过点D作DE⊥OA于点E,与AC交于点F,设点D的横坐标为m.
(1)求抛物线的表达式.
(2)当线段DF的长度取最大时,求D点的坐标.
(3)抛物线上是否存在点D,使得以点O,D,E为顶点的三角形与△BOC相似 若存在,求出m的值;若不存在,请说明理由.
参考答案
一、选择题
1 2 3 4 5 6 7 8 9 10
D D C A C A A B B C
1.D 【解析】把x=2代入方程x2-mx-6=0得22-m×2-6=0,解得m=-1.
2.D 【解析】从左边看外围是长方形,中间有两条看不见的轮廓线(虚线),选项D符合.
4.A 【解析】∵sin A==,故可设BC=k,AB=3k,则AC===2k.∴sin B===.
5.C 【解析】反比例函数y=的图象经过点(2,1),∴1=,∴k=2,故A选项正确;∵反比例函数的解析式为y=,k=2>0,∴图象分布在第一、三象限,故B选项正确;∵k=2>0,∴当x>0时,y随x的增大而减小,故C选项错误;∵k=2>0,∴当x<0时,y随x的增大而减小,故D选项正确.
6.A 【解析】由题意易知△CBD∽△CAE,∴=,即=,解得CB=1 m.
7.A 【解析】∵方程x2-mx+-=0有两个相等的实数根,∴b2-4ac=(-m)2-4(-)=m2-2m+1=(m-1)2=0,∴m=1.∴反比例函数y=(x>0)的图象在第一象限.
8.B 【解析】通过列表法或画树状图法可知,选取两个数共有12种等可能的结果,其中使得二次函数y=ax2+4x+c与x轴有两个不同交点的结果有4种,∴P(二次函数y=ax2+4x+c与x轴有两个不同交点)==.
9.B 【解析】如图,过点D作DE⊥AB于E,作DF⊥BC交BC的延长线于点F,则四边形DEBF是矩形.在Rt△DCF中,∵CD的坡度为1∶0.75,∴=.设DF=4k,CF=3k,则CD=5k.∵CD=45,∴k=9,DF=36,CF=27,∴BE=36,DE=BF=27+60=87.在Rt△ADE中, AE=DE·tan∠ADE≈87×0.53=46.11,∴AB=46.11+36≈82.1(m).
10.C 【解析】由-=-2得4a-b=0,故①正确;由=3得4ac-b2=12a,又4a=b,代入消去b得c=4a+3,故②错误;由图象得,关于x的方程ax2+bx+c=2有两个不相等的实数根,故③正确;由=3得4ac-b2=12a,∴4ac=12a+b2=3b+b2,∵a<0,b<0,c<0,∴4ac<2b+b2 ,故④正确.
二、填空题
11 12 13 14 15 16
-5 0或8 2.5 -1 16 (3,-4)
11.-5 【解析】y=x2+4x+4-5=(x+2)2-5,∴它的最小值为-5.
12.0或8 【解析】根据题意,得(-m)2-4×1×2m=0,即m2-8m=0,所以m=0或m=8.
13.2.5 【解析】设这棵树高x m,则有=,解得x=2.5.
14.-1 【解析】横坐标是负数的点位于第二或第三象限,由题意得点C一定位于第三象限,结合反比例函数的图象和性质,可得该反比例函数的图象经过点B和点C,所以k=3×2=-6m,所以m=-1.
15.16 【解析】设CD=x(米).在Rt△BCD中,∵tan∠CBD=,∴BC==≈=.在Rt△ACD中,∵tan∠CAD=,∴AC=≈=.∵AC-BC=AB,∴x-x=30,解得x=16.
16.(3,-4) 【解析】过点A作AD⊥BC于点D,∵AB=AC,∴BD=CD,∵反比例函数y=的图象经过点A,B,A(1,4),∴B(-1,-4),∵CD=BD=1+1=2,∴BC=2BD=4,∵BC∥x轴,∴C(3,-4).
三、解答题
17.解:原式=()2+×-1(3分)
=+-1=1.(6分)
18.解:(1)正三棱柱,72.(2分)
(2)如图,在俯视图中,过点E作EH⊥FG,则AB=EH.
∵△EFG是等边三角形,且EF=FG=GE=4,
∴∠EFG=60°,∴EH=EF·sin 60°=4×=2.
即AB=2.(6分)
19.解:(1).(2分)
(2)画树状图为:
(4分)
由上图可知,共有16种等可能的结果,其中他们第二次选课相同的结果数为4,所以他们第二次选课相同的概率==.(6分)
20.解:如图,连接AD和EF,则点G是它们的交点,
∵∠BAC=90°,DE⊥AB,DF⊥AC,∴四边形AEDF是矩形,∴EF=AD,
在Rt△ABC中,AB=9,AC=12,∴BC==15,∴当AD⊥BC时,AD的长最短,即此时FG的长最短,
∵S△ABC=AC·AB=BC·AD,∴9×12=15×AD,∴AD==,∴EF的最小值为,
∵点G是AD与EF的交点,∴FG的最小值为.(6分)
21.解:(1)∵DE是BC的垂直平分线,∴BE=CE.
∴∠EBC=∠ECB.
∵AB=AD,∴∠ABC=∠ADB,
∴△FDB∽△ABC.(3分)
(2)∵△FDB∽△ABC,
∴==.
∴AB=2FD.
∵AB=AD,∴AD=2FD.
∴DF=AF.(8分)
22.解:(1)m=6,C点坐标为(2,0).(2分)
(2)设直线AB对应的函数表达式为y=kx+b.
将A(4,),C(2,0)代入得,解得,
∴直线AB对应的函数表达式为y=x-.(4分)
∵点D在线段AB上,可设D(a,a-)(0∵DE∥y轴,交反比例函数图象于点E,∴E(a,).
∴S△ODE=a(-a+)=-a2+a+3=-(a-1)2+.
∴当a=1时,△ODE面积的最大值为.(8分)
23.解:(1)如图③中,∵BC⊥AC,垂足为C,∠OAC=30°,
∵sin∠OAC=,∴OC=OA·sin∠OAC=24·sin 30°=12(cm).(4分)
(2)如图,过B'作B'D⊥AC交AC的延长线于D,延长B'O交AC于E.
则∠B'EA=∠BOA=120°,∠B'DE=∠OCA=90° ,OB'=OB=24 cm.
∵∠B'EA=∠OCA+∠COE,
∴∠COE=∠B'EA-∠OCA=120°-90°=30°.
在Rt△OCE中,cos∠COE=,∴OE===8 cm.
∴B'E=B'O+OE=8+24.
∵∠B'DE=∠OCA,∴OC∥B'D,
∴=,∴=,解得B'D=12+12.
即点B'到AC的距离为(12+12) cm.(10分)
24.解:(1)证明:∵四边形ABCD是菱形,∠BAD=60°,
∴∠ABC=∠ADC=120°.
∵CE⊥AB,CF⊥AD,∴CE=CF.
∵H为对角线AC的中点,∴EH=FH=AC.
∵∠CAE=30°,∴CE=AC,
∴CE=EH=CF=FH,
∴四边形CEHF是菱形.(5分)
(2)∵CE⊥AB,CE=4,△ACE的面积为16,
∴AE=8,∴AC==4.
如图,连接BD,则BD⊥AC,AH=AC=2.
∵∠AHB=∠AEC=90°,∠BAH=∠EAC,
∴△ABH∽△ACE,∴=,
∴=.∴BH=.
∴BD=2BH=2.
∴菱形ABCD的面积=AC·BD=×2×4=20.(10分)
25.解:(1)设OB=t,则OA=2t,则点A、B的坐标分别为(2t,0)、(-t,0),
则x==(2t-t),解得t=1.
故点A、B的坐标分别为(2,0)、(-1,0),
则抛物线的表达式为y=a(x-2)(x+1)=ax2+bx+2,
解得a=-1.
故抛物线的表达式为y=-x2+x+2.(3分)
(2)对于y=-x2+x+2,令x=0,则y=2,故点C(0,2).
由点A、C的坐标得,直线AC的表达式为y=-x+2,
设点D的横坐标为m,则点D(m,-m2+m+2),则点F(m,-m+2),
则DF=-m2+m+2-(-m+2)=-m2+2m,
∵-1<0,故DF有最大值,此时m=1,∴点D(1,2).(7分)
(3)存在,理由:
点D(m,-m2+m+2)(m>0),则OE=m,DE=-m2+m+2,
以点O,D,E为顶点的三角形与△BOC相似,
则=或,即=2或,即=2或,
解得m=1或-2(舍去)或或(舍去),
故m=1或.(12分)
时间:90分钟 满分:120分 考试范围:上册全部~下册第二章
一、选择题(本题共10小题,每小题3分,共30分)
1.已知关于x的方程x2-mx-6=0的一个根为2,则m的值是 ( )
A.2 B.-2 C.1 D.-1
2.如图所示,该几何体的左视图是 ( )
A. B. C. D.
3.下列命题中,正确的是 ( )
A.菱形的对角线相等 B.矩形的对角线互相垂直
C.正方形的对角线相等且互相垂直 D.正方形的面积等于对角线的平方
4.在Rt△ABC中,∠C=90°,sin A=,那么sin B的值是 ( )
A. B.2 C. D.3
5.反比例函数y=的图象经过点(2,1),则下列说法错误的是 ( )
A.k=2 B.函数图象分布在第一、三象限
C.当x>0时,随x的增大而增大 D.当x>0时,y随x的增大而减小
6.如图,阳光透过窗户洒落在地面上,已知窗户AB高1.5 m,光亮区的顶端距离墙角3 m,光亮区的底端距离墙角1.2 m,则窗户的底端距离地面的高度(BC)为 ( )
A.1 m B.1.2 m C.1.5 m D.2.4 m
7.若关于x的方程x2-mx+-=0有两个相等的实数根,则反比例函数y=(x>0)的图象在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8.从1,2,3,4四个数中随机选取两个不同的数,分别记为a,c,则二次函数y=ax2+4x+c的图象与x轴有两个不同交点的概率为 ( )
A. B. C. D.
9.如图,在距某居民楼AB楼底B点左侧水平距离60 m的C点处有一个山坡,山坡CD的坡度(或坡比) i=1∶0.75,山坡坡底C点到坡顶D点的距离CD=45 m,在坡顶D点处测得居民楼楼顶A点的仰角为28°,居民楼AB与山坡CD的剖面在同一平面内,则居民楼AB的高度约为(参考数据:sin 28°≈0.47,cos 28°≈0.88,tan 28°≈0.53) ( )
A.76.9 m B.82.1 m C.94.8 m D.112.6 m
10.抛物线y=ax2+bx+c的对称轴是直线x=-2,抛物线与x轴的一个交点在点(-4,0)和点(-3,0)之间,其部分图象如图所示,下列结论中正确的有 ( )
①4a-b=0;②c≤3a;③关于x的方程ax2+bx+c=2有两个不相等的实数根;④b2+2b> 4ac.
A.1个 B.2个 C.3个 D.4个
二、填空题(本题共6小题,每小题3分,共18分)
11.抛物线y=x2+4x-1的最小值为 .
12.关于x的一元二次方程x2-mx+2m=0有两个相等的实数根,则实数m的值为 .
13.如图,为了测量一棵树的高度,小梦在同一时间、同一地点测得小兰的身高为1.5 m,影长是2.4 m,树的影长为 4 m,则这棵树的高度为 m.
14.在平面直角坐标系中,点A(-2,1),B(3,2),C(-6,m)分别在三个不同的象限.若反比例函数y=(k≠0)的图象经过其中两点,则m的值为 .
15.如图,为测量建筑物CD的高度,在A点测得建筑物顶部D的仰角为22°,再向建筑物CD前进30米到达B点,测得建筑物顶部D的仰角为58°(A,B,C三点在一条直线上),则建筑物CD的高度等于 米.(结果保留整数.参考数据:sin 22°≈0.37,cos 22°≈0.93,tan 22°≈0.40,sin 58°≈0.85,cos 58°≈0.53,tan 58°≈1.60)
16.如图,在平面直角坐标系中,等腰△ABC的腰AB经过原点O,底边BC与x轴平行,反比例函数y=的图象经过点A,B,A(1,4),则点C的坐标为 .
三、解答题(本大题共9小题,共72分)
17.(6分)计算:cos245°+tan 60°·cos 30°-(2021-π)0.
18.(6分)一个几何体的三种视图如图所示.
(1)这个几何体的名称是 ,其侧面积为 ;
(2)求出左视图中AB的长.
19.(6分)某学校课后开设了五门课程供学生选择,五门课程分别是A:课后作业辅导;B:书法;C:阅读;D:绘画;E:乐器.学生需要从中选两门课程.
(1)若学生甲选第一门课程时任选一门,则甲选中课程A的概率是 .
(2)若学生甲和乙第一次都选择了课程E,第二次都从剩余课程里随机选一门课程,则他们第二次选课相同的概率是多少 请用列表或画树状图的方法加以说明.
20.(6分)如图,在Rt△ABC中,∠BAC=90°,AB=9,AC=12,点D是斜边BC上的一个动点,过点D分别作DE⊥AB于点E,DF⊥AC于点F,点G是四边形DEAF的对角线的交点,求线段GF的最小值.
21.(8分)如图,在△ABC中,BC的垂直平分线分别交BC,AC于点D,E,BE交AD于点F,AB=AD.
(1)判断△FDB与△ABC是否相似,并说明理由.
(2)AF与DF相等吗 为什么
22.(8分)如图,在平面直角坐标系xOy中,反比例函数y=(x>0)的图象经过点A(4,),点B在y轴的负半轴上,AB交x轴于点C,C为线段AB的中点.
(1)m= ,点C 的坐标为 ;
(2)若点D为线段AB上的一个动点,过点D作DE∥y轴,交反比例函数的图象于点E,求△ODE面积的最大值.
23.(10分)小华同学将笔记本电脑水平放置在桌面上,当显示屏的边缘线OB与底板的边缘线OA所在水平线的夹角为120°时感觉最舒适(如图①),侧面示意图为图②;使用时为了散热,他在底板下面垫入散热架,如图③,点B,O,C在同一直线上,OA=OB=24 cm,BC⊥AC,∠OAC=30°.
(1)求OC的长;
(2)如图④,垫入散热架后,要使显示屏的边缘线OB'与水平线的夹角仍保持120°,求点B'到AC的距离.(结果保留根号)
24.(10分)如图,四边形ABCD是菱形,点H为对角线AC的中点,点E在AB的延长线上,CE⊥AB,垂足为E,点F在AD的延长线上,CF⊥AD,重足为F.
(1)若∠BAD=60°,求证:四边形CEHF是菱形.
(2)若CE=4,△ACE的面积为16,求菱形ABCD的面积.
25.(12分)如图,抛物线y=ax2+bx+2与x轴交于A,B两点,且OA=2OB,与y轴交于点C,连接BC,抛物线的对称轴为直线x=,D为第一象限内抛物线上一动点,过点D作DE⊥OA于点E,与AC交于点F,设点D的横坐标为m.
(1)求抛物线的表达式.
(2)当线段DF的长度取最大时,求D点的坐标.
(3)抛物线上是否存在点D,使得以点O,D,E为顶点的三角形与△BOC相似 若存在,求出m的值;若不存在,请说明理由.
参考答案
一、选择题
1 2 3 4 5 6 7 8 9 10
D D C A C A A B B C
1.D 【解析】把x=2代入方程x2-mx-6=0得22-m×2-6=0,解得m=-1.
2.D 【解析】从左边看外围是长方形,中间有两条看不见的轮廓线(虚线),选项D符合.
4.A 【解析】∵sin A==,故可设BC=k,AB=3k,则AC===2k.∴sin B===.
5.C 【解析】反比例函数y=的图象经过点(2,1),∴1=,∴k=2,故A选项正确;∵反比例函数的解析式为y=,k=2>0,∴图象分布在第一、三象限,故B选项正确;∵k=2>0,∴当x>0时,y随x的增大而减小,故C选项错误;∵k=2>0,∴当x<0时,y随x的增大而减小,故D选项正确.
6.A 【解析】由题意易知△CBD∽△CAE,∴=,即=,解得CB=1 m.
7.A 【解析】∵方程x2-mx+-=0有两个相等的实数根,∴b2-4ac=(-m)2-4(-)=m2-2m+1=(m-1)2=0,∴m=1.∴反比例函数y=(x>0)的图象在第一象限.
8.B 【解析】通过列表法或画树状图法可知,选取两个数共有12种等可能的结果,其中使得二次函数y=ax2+4x+c与x轴有两个不同交点的结果有4种,∴P(二次函数y=ax2+4x+c与x轴有两个不同交点)==.
9.B 【解析】如图,过点D作DE⊥AB于E,作DF⊥BC交BC的延长线于点F,则四边形DEBF是矩形.在Rt△DCF中,∵CD的坡度为1∶0.75,∴=.设DF=4k,CF=3k,则CD=5k.∵CD=45,∴k=9,DF=36,CF=27,∴BE=36,DE=BF=27+60=87.在Rt△ADE中, AE=DE·tan∠ADE≈87×0.53=46.11,∴AB=46.11+36≈82.1(m).
10.C 【解析】由-=-2得4a-b=0,故①正确;由=3得4ac-b2=12a,又4a=b,代入消去b得c=4a+3,故②错误;由图象得,关于x的方程ax2+bx+c=2有两个不相等的实数根,故③正确;由=3得4ac-b2=12a,∴4ac=12a+b2=3b+b2,∵a<0,b<0,c<0,∴4ac<2b+b2 ,故④正确.
二、填空题
11 12 13 14 15 16
-5 0或8 2.5 -1 16 (3,-4)
11.-5 【解析】y=x2+4x+4-5=(x+2)2-5,∴它的最小值为-5.
12.0或8 【解析】根据题意,得(-m)2-4×1×2m=0,即m2-8m=0,所以m=0或m=8.
13.2.5 【解析】设这棵树高x m,则有=,解得x=2.5.
14.-1 【解析】横坐标是负数的点位于第二或第三象限,由题意得点C一定位于第三象限,结合反比例函数的图象和性质,可得该反比例函数的图象经过点B和点C,所以k=3×2=-6m,所以m=-1.
15.16 【解析】设CD=x(米).在Rt△BCD中,∵tan∠CBD=,∴BC==≈=.在Rt△ACD中,∵tan∠CAD=,∴AC=≈=.∵AC-BC=AB,∴x-x=30,解得x=16.
16.(3,-4) 【解析】过点A作AD⊥BC于点D,∵AB=AC,∴BD=CD,∵反比例函数y=的图象经过点A,B,A(1,4),∴B(-1,-4),∵CD=BD=1+1=2,∴BC=2BD=4,∵BC∥x轴,∴C(3,-4).
三、解答题
17.解:原式=()2+×-1(3分)
=+-1=1.(6分)
18.解:(1)正三棱柱,72.(2分)
(2)如图,在俯视图中,过点E作EH⊥FG,则AB=EH.
∵△EFG是等边三角形,且EF=FG=GE=4,
∴∠EFG=60°,∴EH=EF·sin 60°=4×=2.
即AB=2.(6分)
19.解:(1).(2分)
(2)画树状图为:
(4分)
由上图可知,共有16种等可能的结果,其中他们第二次选课相同的结果数为4,所以他们第二次选课相同的概率==.(6分)
20.解:如图,连接AD和EF,则点G是它们的交点,
∵∠BAC=90°,DE⊥AB,DF⊥AC,∴四边形AEDF是矩形,∴EF=AD,
在Rt△ABC中,AB=9,AC=12,∴BC==15,∴当AD⊥BC时,AD的长最短,即此时FG的长最短,
∵S△ABC=AC·AB=BC·AD,∴9×12=15×AD,∴AD==,∴EF的最小值为,
∵点G是AD与EF的交点,∴FG的最小值为.(6分)
21.解:(1)∵DE是BC的垂直平分线,∴BE=CE.
∴∠EBC=∠ECB.
∵AB=AD,∴∠ABC=∠ADB,
∴△FDB∽△ABC.(3分)
(2)∵△FDB∽△ABC,
∴==.
∴AB=2FD.
∵AB=AD,∴AD=2FD.
∴DF=AF.(8分)
22.解:(1)m=6,C点坐标为(2,0).(2分)
(2)设直线AB对应的函数表达式为y=kx+b.
将A(4,),C(2,0)代入得,解得,
∴直线AB对应的函数表达式为y=x-.(4分)
∵点D在线段AB上,可设D(a,a-)(0
∴S△ODE=a(-a+)=-a2+a+3=-(a-1)2+.
∴当a=1时,△ODE面积的最大值为.(8分)
23.解:(1)如图③中,∵BC⊥AC,垂足为C,∠OAC=30°,
∵sin∠OAC=,∴OC=OA·sin∠OAC=24·sin 30°=12(cm).(4分)
(2)如图,过B'作B'D⊥AC交AC的延长线于D,延长B'O交AC于E.
则∠B'EA=∠BOA=120°,∠B'DE=∠OCA=90° ,OB'=OB=24 cm.
∵∠B'EA=∠OCA+∠COE,
∴∠COE=∠B'EA-∠OCA=120°-90°=30°.
在Rt△OCE中,cos∠COE=,∴OE===8 cm.
∴B'E=B'O+OE=8+24.
∵∠B'DE=∠OCA,∴OC∥B'D,
∴=,∴=,解得B'D=12+12.
即点B'到AC的距离为(12+12) cm.(10分)
24.解:(1)证明:∵四边形ABCD是菱形,∠BAD=60°,
∴∠ABC=∠ADC=120°.
∵CE⊥AB,CF⊥AD,∴CE=CF.
∵H为对角线AC的中点,∴EH=FH=AC.
∵∠CAE=30°,∴CE=AC,
∴CE=EH=CF=FH,
∴四边形CEHF是菱形.(5分)
(2)∵CE⊥AB,CE=4,△ACE的面积为16,
∴AE=8,∴AC==4.
如图,连接BD,则BD⊥AC,AH=AC=2.
∵∠AHB=∠AEC=90°,∠BAH=∠EAC,
∴△ABH∽△ACE,∴=,
∴=.∴BH=.
∴BD=2BH=2.
∴菱形ABCD的面积=AC·BD=×2×4=20.(10分)
25.解:(1)设OB=t,则OA=2t,则点A、B的坐标分别为(2t,0)、(-t,0),
则x==(2t-t),解得t=1.
故点A、B的坐标分别为(2,0)、(-1,0),
则抛物线的表达式为y=a(x-2)(x+1)=ax2+bx+2,
解得a=-1.
故抛物线的表达式为y=-x2+x+2.(3分)
(2)对于y=-x2+x+2,令x=0,则y=2,故点C(0,2).
由点A、C的坐标得,直线AC的表达式为y=-x+2,
设点D的横坐标为m,则点D(m,-m2+m+2),则点F(m,-m+2),
则DF=-m2+m+2-(-m+2)=-m2+2m,
∵-1<0,故DF有最大值,此时m=1,∴点D(1,2).(7分)
(3)存在,理由:
点D(m,-m2+m+2)(m>0),则OE=m,DE=-m2+m+2,
以点O,D,E为顶点的三角形与△BOC相似,
则=或,即=2或,即=2或,
解得m=1或-2(舍去)或或(舍去),
故m=1或.(12分)
同课章节目录
