期中闯关测试卷 1.1-4.5(含答案) 2024-2025北师大版九年级数学上册
文档属性
| 名称 | 期中闯关测试卷 1.1-4.5(含答案) 2024-2025北师大版九年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 179.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 16:00:21 | ||
图片预览




文档简介
期中测试卷
时间:90分钟 满分:120分 考试范围:1.1~4.5
题序 一 二 三 评卷人 总分
得分
一、选择题(本题共10小题,每小题3分,共30分)
1.已知线段a,b,c,d成比例,其中a=3 cm,b=2 cm,c=6 cm,则d的长度为 ( )
A.4 cm B.5 cm C.6 cm D.9 cm
2.方程(x-2)2=x-2的解是 ( )
A.x=3 B.x=2 C.x1=2,x2=3 D.x1=2,x2=0
3.如果=,那么的值是 ( )
A. B. C. D.
4.小明制作了5张卡片,上面分别写了一个条件:①AB=BC;②AB⊥BC;③AD=BC;④AC⊥BD;⑤AC=BD.从中随机抽取一张卡片,能判定 ABCD是菱形的概率为 ( )
A. B. C. D.
5.若关于x的一元二次方程(k-1)x2+x-k2=0的一个根为2,则k的值为 ( )
A.1 B.3 C.1或3 D.0
6.如图,已知AB∥CD∥EF, = ,BE=12,那么CE的长为 ( )
A.2 B.4 C. D.
7.在一个不透明的布袋中装有60个白球和若干个黑球,球除颜色外其他都相同,小红每次摸出一个球并放回,通过多次试验后发现,摸到黑球的频率稳定在0.6左右,则布袋中黑球的个数可能为 ( )
A.24 B.36 C.40 D.90
8.定义运算:m☆n=mn2-mn-1.例如: 4☆2=4×22-4×2-1=7.方程1☆x=0的根的情况为 ( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.无实数根 D.只有一个实数根
9.如图,矩形ABCD的周长是20 cm,分别以AB,AD为边向外作正方形ABEF和正方形ADGH.若正方形ABEF和正方形ADGH的面积之和为68 cm2,则矩形ABCD的面积为 ( )
A.9 cm2 B.16 cm2 C.21 cm2 D.24 cm2
10.如图,菱形ABCD的边长为2,∠ABC=60°,点E,F在对角线BD上运动,且EF=2,连接AE,AF,则△AEF周长的最小值是 ( )
A.4 B.4+ C.2+2 D.6
二、填空题(本题共6小题,每小题3分,共18分)
11.若方程x2+4x+n=0可以配方成(x+m)2=3,则(n-m)2020= .
12.如图,已知P,Q是线段AB上的两点,==且PQ=4,则AB= .
13.毛泽东在《沁园春·雪》中提到五位历史名人:秦始皇、汉武帝、唐太宗、宋太祖、成吉思汗.小明将这五位名人的简介分别写在五张完全相同的知识卡片上,小哲从中随机抽取一张,卡片上介绍的人物是唐朝以后出生的概率为 .
14.已知x1,x2是方程x2-2x-5=0的两根,则-x1+x2的值为 .
15.如图,在四边形ABCD中,∠A=∠B=90°,AB=5,AD=3,BC=2,点P是AB上一点,若△PAD∽△CBP,则PA的长为 .
16.四张形状、大小、背面完全相同的卡片上分别标有数字-2,-1,0,1,将卡片洗匀后背面朝上放在桌面上,从中任意抽取两张,则所抽卡片上的数字都是方程x2+x-2=0的解的概率是 .
三、解答题(本大题共9小题,共72分)
17.(6分)用合适的方法解方程:x2-1=2(x-1).
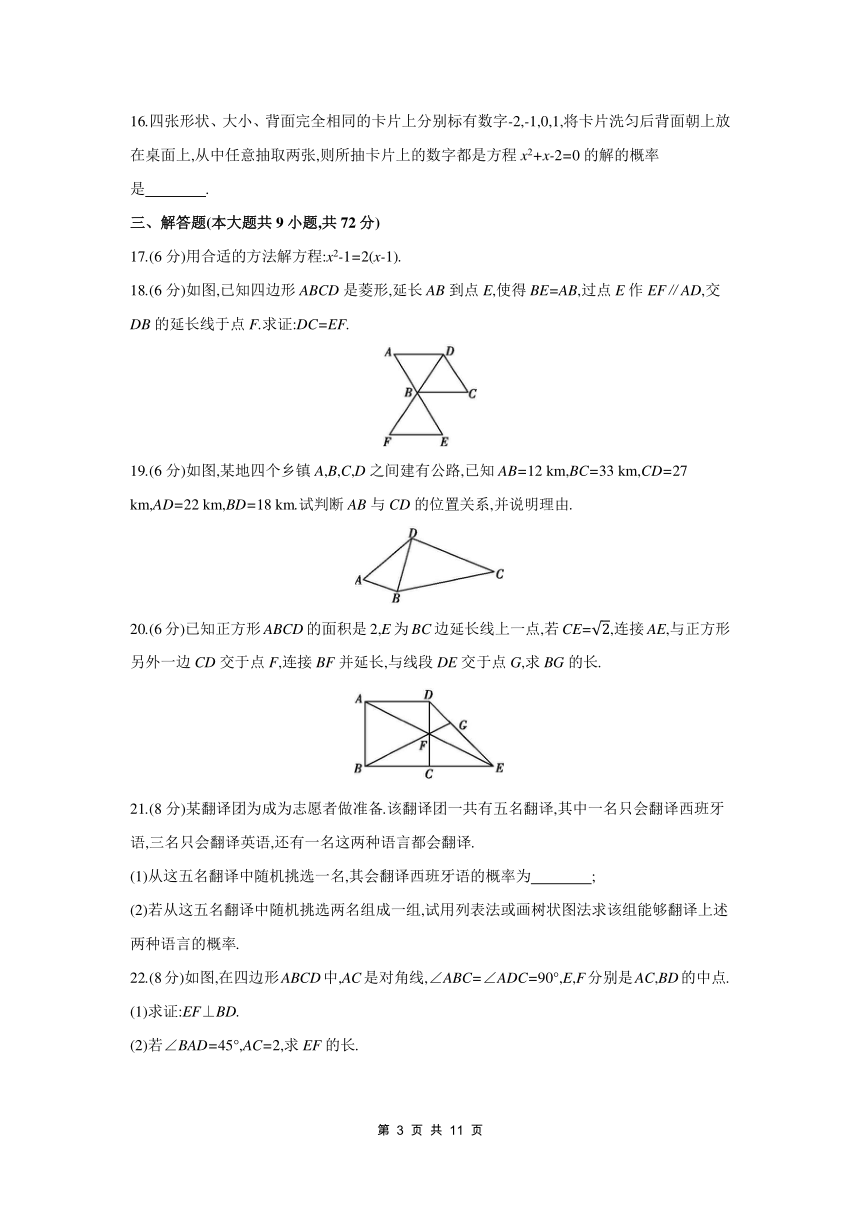
18.(6分)如图,已知四边形ABCD是菱形,延长AB到点E,使得BE=AB,过点E作EF∥AD,交DB的延长线于点F.求证:DC=EF.
19.(6分)如图,某地四个乡镇A,B,C,D之间建有公路,已知AB=12 km,BC=33 km,CD=27 km,AD=22 km,BD=18 km.试判断AB与CD的位置关系,并说明理由.
20.(6分)已知正方形ABCD的面积是2,E为BC边延长线上一点,若CE=,连接AE,与正方形另外一边CD交于点F,连接BF并延长,与线段DE交于点G,求BG的长.
21.(8分)某翻译团为成为志愿者做准备.该翻译团一共有五名翻译,其中一名只会翻译西班牙语,三名只会翻译英语,还有一名这两种语言都会翻译.
(1)从这五名翻译中随机挑选一名,其会翻译西班牙语的概率为 ;
(2)若从这五名翻译中随机挑选两名组成一组,试用列表法或画树状图法求该组能够翻译上述两种语言的概率.
22.(8分)如图,在四边形ABCD中,AC是对角线,∠ABC=∠ADC=90°,E,F分别是AC,BD的中点.
(1)求证:EF⊥BD.
(2)若∠BAD=45°,AC=2,求EF的长.
23.(10分)如图,在△ABC中,AB=AC,点E在边BC上移动(点E不与点B,C重合),满足∠DEF=∠B,且点D,F分别在边AB,AC上.
(1)求证:△BDE∽△CEF.
(2)当点E移动到BC的中点时,求证:FE平分∠DFC.
24.(10分)某商场在去年底以每件80元的进价购进一批同型号的服装,一月份以每件150元的售价销售了320件,二、三月份该服装畅销,销量持续走高,在售价不变的情况下,三月份的销量达到了500件.
(1)求二、三月份服装销售量的平均月增长率.
(2)四月份起商场因换季清仓采用降价促销的方式,经调查发现,在三月份销量的基础上,该服装售价每降价5元,月销售量增加10件,当每件降价多少元时,四月份可获利12000元
25.(12分)(1)如图1,在△ABC中,点D,E,Q分别在AB,AC,BC上,且DE∥BC,AQ交DE于点P,求证:=.
(2)如图2,在△ABC中,∠BAC=90°,正方形DEFG的四个顶点在△ABC的边上,连接AG,AF分别交DE于M,N两点.
①如图2,若AB=AC=1,直接写出MN的长;
②如图3,求证:MN2=DM·EN.
参考答案
一、选择题
1 2 3 4 5 6 7 8 9 10
A C C B B C D A B D
1.A 【解析】∵a,b,c,d成比例,∴a∶b=c∶d,即3∶2=6∶d,∴d=4 cm.
2.C 【解析】原方程移项,得(x-2)2-(x-2)=0,左边因式分解得(x-2)(x-2-1)=0,∴x1=2,x2=3.
3.C 【解析】∵=,∴5(a-b)=3a,即2a=5b,∴=.
4.B 【解析】能判断 ABCD是菱形的有①AB=BC,④AC⊥BD,所以能判定 ABCD是菱形的概率为.
5.B 【解析】将x=2代入方程得4(k-1)+1-k2=0,即k2-4k+3=0,解得k1=3,k2=1(不合题意,舍去).
6.C 【解析】∵AB∥CD∥EF,=,BE=12,∴= =,即=,∴BC=,∴CE=BE-BC=12-=.
7.D 【解析】设布袋中黑球有x个,则=0.6,解得x=90.
8.A 【解析】方程1☆x=0可变形为x2-x-1=0,∵Δ=(-1)2-4×1×(-1)=5>0,∴方程有两个不相等的实数根.
9.B 【解析】设AB=x cm,AD=y cm,则x+y=10,x2+y2=(x+y)2-2xy=68,即102-2xy=68,∴xy=16,即矩形ABCD的面积为16 cm2.
10.D 【解析】如图,作AH∥BD,使得AH=EF=2,连接CH交BD于F,则此时AE+AF的值最小,即△AEF的周长最小.∵AH=EF,AH∥EF,∴四边形EFHA是平行四边形,∴EA=FH.∵FA=FC,∴AE+AF=FH+CF=CH.∵菱形ABCD的边长为2,∠ABC=60°,∴AC=AB=2.∵四边形ABCD是菱形,∴AC⊥BD,∵AH∥DB,∴AC⊥AH.∴∠CAH=90°.在Rt△CAH中,CH===4,∴AE+AF的最小值是4.∴△AEF的周长的最小值=4+2=6.
二、填空题
11 12 13 14 15 16
1 18 7 2或3
11.1 【解析】∵x2+4x+n=0,∴(x+2)2=4-n,∵(x+m)2=3,∴m=2,4-n=3,∴n=1,∴(n-m)2020=1.
12.18 【解析】∵=,PQ=4,∴PB=3PQ=3×4=12.∵=,∴AB=3AP,∴AP+12=3AP,∴AP=6,∴AB=18.
13. 【解析】在秦始皇、汉武帝、唐太宗、宋太祖、成吉思汗5人中,唐朝以后出生的有2人,∴随机抽取一张,所抽到的人物为唐朝以后出生的概率为.
14.7 【解析】∵x1,x2是方程x2-2x-5=0的两根,∴x1+x2=2,-2x1-5=0,∴-2x1=5.∴-x1+x2=-2x1+x1+x2=5+2=7.
15.2或3 【解析】设PA=x,∵△PAD∽△CBP,∴=,∴=,即x(5-x)=6,∴x2-5x+6=0,解得x=2或3,经检验x=2或3都是原方程的解,故答案为2或3.
16. 【解析】解方程x2+x-2=0的解为x1=1,x2=-2.通过列表或画树状图可知,抽取的两张卡片共有12种等可能结果,其中解为1或-2的结果共有2种,故P(所抽卡片上的数字都是方程x2+x-2=0的解)==.
三、解答题
17.解:原方程可变形为(x+1)(x-1)-2(x-1)=0.
左边提公因式,得(x-1)(x+1-2)=0,即(x-1)2=0.
∴x1=x2=1.(6分)
18. 证明:∵四边形ABCD是菱形,
∴AD=DC.
∵AD∥EF,∴∠A=∠E,∠ADB=∠DFE.
又∵AB=BE,
∴△ABD≌△EBF(AAS).(4分)
∴AD=EF,
∴DC=EF.(6分)
19.解:AB与CD平行.理由如下:(1分)
由已知,得==,==,==,
∴==.(4分)
∴△ABD∽△BDC,
∴∠ABD=∠CDB,
∴AB∥CD.(6分)
20.解:如图,延长AD,BG相交于点H.
∵正方形ABCD的面积是2,∴AB=BC=CD=DA=.
又∵CE=,△EFC∽△EAB,∴==,即F是CD的中点.
∵AH∥BE,∴∠H=∠FBC,∠BCF=∠HDF=90°.∴△BCF≌△HDF.(3分)
∴DH=BC=.
∵AH∥BE,∴∠H=∠FBC,∠HDG=∠BEG.∴△HDG∽△BEG,∴==.
在Rt△ABH中,BH==,∴BG=BH=. (6分)
21.解:(1);(2分)
(2)只会翻译西班牙语的这名翻译用A表示,只会翻译英语的三名翻译分别用B1,B2,B3表示,两种语言都会翻译的这名翻译用C表示,列表如下:
A B1 B2 B3 C
A (A,B1) (A,B2) (A,B3) (A,C)
B1 (B1,A) (B1,B2) (B1,B3) (B1,C)
B2 (B2,A) (B2,B1) (B2,B3) (B2,C)
B3 (B3,A) (B3,B1) (B3,B2) (B3,C)
C (C,A) (C,B1) (C,B2) (C,B3)
(6分)
由表可知,共有20种等可能的结果,其中该组能够翻译上述两种语言的结果有14种,
∴P(该组能够翻译上述两种语言)==.(8分)
22.解:(1)证明:∵∠ABC=∠ADC=90°,E为AC的中点,
∴BE=AC,DE=AC,
∴BE=DE,
又∵F为BD的中点,∴EF⊥BD. (3分)
(2)∵AE=BE,∴∠BAE=∠ABE,
∵∠BEC=∠BAC+∠ABE,
∴∠BEC=2∠BAC,
同理,∠DEC=2∠DAC,
∴∠BED=∠BEC+∠DEC=2(∠BAC+∠DAC)=2×45°=90°,
∵AC=2,∴BE=DE=1,∴∠EBD=45°,∴BF=EF,
设BF=EF=x,
∴2x2=12,∴x=,
∴EF=.(8分)
23.解:(1)∵AB=AC,∴∠B=∠C.
∵∠DEF+∠CEF=∠B+∠BDE,∠DEF=∠B,
∴∠CEF=∠BDE,
∴△BDE∽△CEF.(4分)
(2)由(1)得=,
∵E是BC的中点,∴BE=CE,∴=,即=.(6分)
∵∠C=∠DEF,∴△EDF∽△CEF,
∴∠CFE=∠EFD,即FE平分∠DFC.(10分)
24.解:(1)设二、三月份销售量的平均月增长率为x,
则依题意得320(1+x)2=500.(3分)
解得x1=0.25,x2=-2.25(舍去).
答:二、三月份销售量的平均月增长率为25%.(5分)
(2)设每件降价y元,
根据题意,得(500+10×)(150-y-80)=12000,(8分)
整理得y2+180y-11500=0.
解得y1=50,y2=-230(舍去).
答:每件降价50元,四月份可获利12000元.(10分)
25.解:(1)证明:在△ABQ和△ADP中,∵DP∥BQ,
∴△ADP∽△ABQ,∴=.
同理在△ACQ和△APE中,
=,∴=.(4分)
(2)①作AQ⊥BC于点Q.
∵AB=AC=1,
∴BC边上的高AQ=.
∵DE=DG=GF=EF=BG=CF,
∴DE∶BC=1∶3.
又∵DE∥BC,∴AD∶AB=1∶3,∴AD=,DE=,
∴DE边上的高为,
∴MN∶GF=∶.
∴MN∶=∶,∴MN=;(7分)
②证明:∵∠B+∠C=90°,∠CEF+∠C=90°,∴∠B=∠CEF.
又∵∠BGD=∠EFC,∴△BGD∽△EFC,∴=.
∴DG·EF=CF·BG.
又∵DG=GF=EF,∴GF2=CF·BG.
由(1)得,==,
∴·=·,
∴()2=·.
∵GF2=CF·BG,∴MN2=DM·EN.(12分)
时间:90分钟 满分:120分 考试范围:1.1~4.5
题序 一 二 三 评卷人 总分
得分
一、选择题(本题共10小题,每小题3分,共30分)
1.已知线段a,b,c,d成比例,其中a=3 cm,b=2 cm,c=6 cm,则d的长度为 ( )
A.4 cm B.5 cm C.6 cm D.9 cm
2.方程(x-2)2=x-2的解是 ( )
A.x=3 B.x=2 C.x1=2,x2=3 D.x1=2,x2=0
3.如果=,那么的值是 ( )
A. B. C. D.
4.小明制作了5张卡片,上面分别写了一个条件:①AB=BC;②AB⊥BC;③AD=BC;④AC⊥BD;⑤AC=BD.从中随机抽取一张卡片,能判定 ABCD是菱形的概率为 ( )
A. B. C. D.
5.若关于x的一元二次方程(k-1)x2+x-k2=0的一个根为2,则k的值为 ( )
A.1 B.3 C.1或3 D.0
6.如图,已知AB∥CD∥EF, = ,BE=12,那么CE的长为 ( )
A.2 B.4 C. D.
7.在一个不透明的布袋中装有60个白球和若干个黑球,球除颜色外其他都相同,小红每次摸出一个球并放回,通过多次试验后发现,摸到黑球的频率稳定在0.6左右,则布袋中黑球的个数可能为 ( )
A.24 B.36 C.40 D.90
8.定义运算:m☆n=mn2-mn-1.例如: 4☆2=4×22-4×2-1=7.方程1☆x=0的根的情况为 ( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.无实数根 D.只有一个实数根
9.如图,矩形ABCD的周长是20 cm,分别以AB,AD为边向外作正方形ABEF和正方形ADGH.若正方形ABEF和正方形ADGH的面积之和为68 cm2,则矩形ABCD的面积为 ( )
A.9 cm2 B.16 cm2 C.21 cm2 D.24 cm2
10.如图,菱形ABCD的边长为2,∠ABC=60°,点E,F在对角线BD上运动,且EF=2,连接AE,AF,则△AEF周长的最小值是 ( )
A.4 B.4+ C.2+2 D.6
二、填空题(本题共6小题,每小题3分,共18分)
11.若方程x2+4x+n=0可以配方成(x+m)2=3,则(n-m)2020= .
12.如图,已知P,Q是线段AB上的两点,==且PQ=4,则AB= .
13.毛泽东在《沁园春·雪》中提到五位历史名人:秦始皇、汉武帝、唐太宗、宋太祖、成吉思汗.小明将这五位名人的简介分别写在五张完全相同的知识卡片上,小哲从中随机抽取一张,卡片上介绍的人物是唐朝以后出生的概率为 .
14.已知x1,x2是方程x2-2x-5=0的两根,则-x1+x2的值为 .
15.如图,在四边形ABCD中,∠A=∠B=90°,AB=5,AD=3,BC=2,点P是AB上一点,若△PAD∽△CBP,则PA的长为 .
16.四张形状、大小、背面完全相同的卡片上分别标有数字-2,-1,0,1,将卡片洗匀后背面朝上放在桌面上,从中任意抽取两张,则所抽卡片上的数字都是方程x2+x-2=0的解的概率是 .
三、解答题(本大题共9小题,共72分)
17.(6分)用合适的方法解方程:x2-1=2(x-1).
18.(6分)如图,已知四边形ABCD是菱形,延长AB到点E,使得BE=AB,过点E作EF∥AD,交DB的延长线于点F.求证:DC=EF.
19.(6分)如图,某地四个乡镇A,B,C,D之间建有公路,已知AB=12 km,BC=33 km,CD=27 km,AD=22 km,BD=18 km.试判断AB与CD的位置关系,并说明理由.
20.(6分)已知正方形ABCD的面积是2,E为BC边延长线上一点,若CE=,连接AE,与正方形另外一边CD交于点F,连接BF并延长,与线段DE交于点G,求BG的长.
21.(8分)某翻译团为成为志愿者做准备.该翻译团一共有五名翻译,其中一名只会翻译西班牙语,三名只会翻译英语,还有一名这两种语言都会翻译.
(1)从这五名翻译中随机挑选一名,其会翻译西班牙语的概率为 ;
(2)若从这五名翻译中随机挑选两名组成一组,试用列表法或画树状图法求该组能够翻译上述两种语言的概率.
22.(8分)如图,在四边形ABCD中,AC是对角线,∠ABC=∠ADC=90°,E,F分别是AC,BD的中点.
(1)求证:EF⊥BD.
(2)若∠BAD=45°,AC=2,求EF的长.
23.(10分)如图,在△ABC中,AB=AC,点E在边BC上移动(点E不与点B,C重合),满足∠DEF=∠B,且点D,F分别在边AB,AC上.
(1)求证:△BDE∽△CEF.
(2)当点E移动到BC的中点时,求证:FE平分∠DFC.
24.(10分)某商场在去年底以每件80元的进价购进一批同型号的服装,一月份以每件150元的售价销售了320件,二、三月份该服装畅销,销量持续走高,在售价不变的情况下,三月份的销量达到了500件.
(1)求二、三月份服装销售量的平均月增长率.
(2)四月份起商场因换季清仓采用降价促销的方式,经调查发现,在三月份销量的基础上,该服装售价每降价5元,月销售量增加10件,当每件降价多少元时,四月份可获利12000元
25.(12分)(1)如图1,在△ABC中,点D,E,Q分别在AB,AC,BC上,且DE∥BC,AQ交DE于点P,求证:=.
(2)如图2,在△ABC中,∠BAC=90°,正方形DEFG的四个顶点在△ABC的边上,连接AG,AF分别交DE于M,N两点.
①如图2,若AB=AC=1,直接写出MN的长;
②如图3,求证:MN2=DM·EN.
参考答案
一、选择题
1 2 3 4 5 6 7 8 9 10
A C C B B C D A B D
1.A 【解析】∵a,b,c,d成比例,∴a∶b=c∶d,即3∶2=6∶d,∴d=4 cm.
2.C 【解析】原方程移项,得(x-2)2-(x-2)=0,左边因式分解得(x-2)(x-2-1)=0,∴x1=2,x2=3.
3.C 【解析】∵=,∴5(a-b)=3a,即2a=5b,∴=.
4.B 【解析】能判断 ABCD是菱形的有①AB=BC,④AC⊥BD,所以能判定 ABCD是菱形的概率为.
5.B 【解析】将x=2代入方程得4(k-1)+1-k2=0,即k2-4k+3=0,解得k1=3,k2=1(不合题意,舍去).
6.C 【解析】∵AB∥CD∥EF,=,BE=12,∴= =,即=,∴BC=,∴CE=BE-BC=12-=.
7.D 【解析】设布袋中黑球有x个,则=0.6,解得x=90.
8.A 【解析】方程1☆x=0可变形为x2-x-1=0,∵Δ=(-1)2-4×1×(-1)=5>0,∴方程有两个不相等的实数根.
9.B 【解析】设AB=x cm,AD=y cm,则x+y=10,x2+y2=(x+y)2-2xy=68,即102-2xy=68,∴xy=16,即矩形ABCD的面积为16 cm2.
10.D 【解析】如图,作AH∥BD,使得AH=EF=2,连接CH交BD于F,则此时AE+AF的值最小,即△AEF的周长最小.∵AH=EF,AH∥EF,∴四边形EFHA是平行四边形,∴EA=FH.∵FA=FC,∴AE+AF=FH+CF=CH.∵菱形ABCD的边长为2,∠ABC=60°,∴AC=AB=2.∵四边形ABCD是菱形,∴AC⊥BD,∵AH∥DB,∴AC⊥AH.∴∠CAH=90°.在Rt△CAH中,CH===4,∴AE+AF的最小值是4.∴△AEF的周长的最小值=4+2=6.
二、填空题
11 12 13 14 15 16
1 18 7 2或3
11.1 【解析】∵x2+4x+n=0,∴(x+2)2=4-n,∵(x+m)2=3,∴m=2,4-n=3,∴n=1,∴(n-m)2020=1.
12.18 【解析】∵=,PQ=4,∴PB=3PQ=3×4=12.∵=,∴AB=3AP,∴AP+12=3AP,∴AP=6,∴AB=18.
13. 【解析】在秦始皇、汉武帝、唐太宗、宋太祖、成吉思汗5人中,唐朝以后出生的有2人,∴随机抽取一张,所抽到的人物为唐朝以后出生的概率为.
14.7 【解析】∵x1,x2是方程x2-2x-5=0的两根,∴x1+x2=2,-2x1-5=0,∴-2x1=5.∴-x1+x2=-2x1+x1+x2=5+2=7.
15.2或3 【解析】设PA=x,∵△PAD∽△CBP,∴=,∴=,即x(5-x)=6,∴x2-5x+6=0,解得x=2或3,经检验x=2或3都是原方程的解,故答案为2或3.
16. 【解析】解方程x2+x-2=0的解为x1=1,x2=-2.通过列表或画树状图可知,抽取的两张卡片共有12种等可能结果,其中解为1或-2的结果共有2种,故P(所抽卡片上的数字都是方程x2+x-2=0的解)==.
三、解答题
17.解:原方程可变形为(x+1)(x-1)-2(x-1)=0.
左边提公因式,得(x-1)(x+1-2)=0,即(x-1)2=0.
∴x1=x2=1.(6分)
18. 证明:∵四边形ABCD是菱形,
∴AD=DC.
∵AD∥EF,∴∠A=∠E,∠ADB=∠DFE.
又∵AB=BE,
∴△ABD≌△EBF(AAS).(4分)
∴AD=EF,
∴DC=EF.(6分)
19.解:AB与CD平行.理由如下:(1分)
由已知,得==,==,==,
∴==.(4分)
∴△ABD∽△BDC,
∴∠ABD=∠CDB,
∴AB∥CD.(6分)
20.解:如图,延长AD,BG相交于点H.
∵正方形ABCD的面积是2,∴AB=BC=CD=DA=.
又∵CE=,△EFC∽△EAB,∴==,即F是CD的中点.
∵AH∥BE,∴∠H=∠FBC,∠BCF=∠HDF=90°.∴△BCF≌△HDF.(3分)
∴DH=BC=.
∵AH∥BE,∴∠H=∠FBC,∠HDG=∠BEG.∴△HDG∽△BEG,∴==.
在Rt△ABH中,BH==,∴BG=BH=. (6分)
21.解:(1);(2分)
(2)只会翻译西班牙语的这名翻译用A表示,只会翻译英语的三名翻译分别用B1,B2,B3表示,两种语言都会翻译的这名翻译用C表示,列表如下:
A B1 B2 B3 C
A (A,B1) (A,B2) (A,B3) (A,C)
B1 (B1,A) (B1,B2) (B1,B3) (B1,C)
B2 (B2,A) (B2,B1) (B2,B3) (B2,C)
B3 (B3,A) (B3,B1) (B3,B2) (B3,C)
C (C,A) (C,B1) (C,B2) (C,B3)
(6分)
由表可知,共有20种等可能的结果,其中该组能够翻译上述两种语言的结果有14种,
∴P(该组能够翻译上述两种语言)==.(8分)
22.解:(1)证明:∵∠ABC=∠ADC=90°,E为AC的中点,
∴BE=AC,DE=AC,
∴BE=DE,
又∵F为BD的中点,∴EF⊥BD. (3分)
(2)∵AE=BE,∴∠BAE=∠ABE,
∵∠BEC=∠BAC+∠ABE,
∴∠BEC=2∠BAC,
同理,∠DEC=2∠DAC,
∴∠BED=∠BEC+∠DEC=2(∠BAC+∠DAC)=2×45°=90°,
∵AC=2,∴BE=DE=1,∴∠EBD=45°,∴BF=EF,
设BF=EF=x,
∴2x2=12,∴x=,
∴EF=.(8分)
23.解:(1)∵AB=AC,∴∠B=∠C.
∵∠DEF+∠CEF=∠B+∠BDE,∠DEF=∠B,
∴∠CEF=∠BDE,
∴△BDE∽△CEF.(4分)
(2)由(1)得=,
∵E是BC的中点,∴BE=CE,∴=,即=.(6分)
∵∠C=∠DEF,∴△EDF∽△CEF,
∴∠CFE=∠EFD,即FE平分∠DFC.(10分)
24.解:(1)设二、三月份销售量的平均月增长率为x,
则依题意得320(1+x)2=500.(3分)
解得x1=0.25,x2=-2.25(舍去).
答:二、三月份销售量的平均月增长率为25%.(5分)
(2)设每件降价y元,
根据题意,得(500+10×)(150-y-80)=12000,(8分)
整理得y2+180y-11500=0.
解得y1=50,y2=-230(舍去).
答:每件降价50元,四月份可获利12000元.(10分)
25.解:(1)证明:在△ABQ和△ADP中,∵DP∥BQ,
∴△ADP∽△ABQ,∴=.
同理在△ACQ和△APE中,
=,∴=.(4分)
(2)①作AQ⊥BC于点Q.
∵AB=AC=1,
∴BC边上的高AQ=.
∵DE=DG=GF=EF=BG=CF,
∴DE∶BC=1∶3.
又∵DE∥BC,∴AD∶AB=1∶3,∴AD=,DE=,
∴DE边上的高为,
∴MN∶GF=∶.
∴MN∶=∶,∴MN=;(7分)
②证明:∵∠B+∠C=90°,∠CEF+∠C=90°,∴∠B=∠CEF.
又∵∠BGD=∠EFC,∴△BGD∽△EFC,∴=.
∴DG·EF=CF·BG.
又∵DG=GF=EF,∴GF2=CF·BG.
由(1)得,==,
∴·=·,
∴()2=·.
∵GF2=CF·BG,∴MN2=DM·EN.(12分)
同课章节目录
