2024-2025北师大版九年级数学上册 月考测试卷(一)1.1-2.4 (含答案)
文档属性
| 名称 | 2024-2025北师大版九年级数学上册 月考测试卷(一)1.1-2.4 (含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 157.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 14:49:18 | ||
图片预览




文档简介
月考测试卷(一)
时间:90分钟 满分:120分 考试范围:1.1~2.4
一、选择题(本题共10小题,每小题3分,共30分)
1.下列方程中,一定是关于x的一元二次方程的是 ( )
A.x2-x(x-1)=0 B.x2+x-2=0
C.x2-2y+1=0 D.x2-=1
2.一元二次方程2x2-x-1=0的根的情况是 ( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.只有一个实数根 D.没有实数根
3.下列命题中正确的是 ( )
A.对角线相等的四边形是矩形
B.对角线互相垂直的四边形是菱形
C.对角线互相垂直平分且相等的四边形是正方形
D.一组对边相等,另一组对边平行的四边形是平行四边形
4.已知关于x的一元二次方程x2+5x-m=0的一个根是2,则另一个根是 ( )
A.-7 B.7 C.3 D.-3
5.用配方法解一元二次方程2x2-3x-1=0,配方正确的是 ( )
A.(x-)2= B.(x-)2=
C.(x-)2= D.(x-)2=
6.如图,把一块长为40 cm,宽为30 cm的矩形硬纸板的四角剪去四个相同小正方形,然后把纸板的四边沿虚线折起,并用胶带粘好,即可做成一个无盖纸盒.若该无盖纸盒的底面积为600 cm2,设剪去的小正方形的边长为x cm,则下列方程正确的是 ( )
A.(30-2x)(40-x)=600 B.(30-x)(40-x)=600
C.(30-x)(40-2x)=600 D.(30-2x)(40-2x)=600
7.菱形ABCD的边长为,对角线AC,BD交于点O,OA=1,则菱形ABCD的面积为 ( )
A. B.2 C.2 D.4
8.在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别是AO,AD的中点,连接EF,若AB=6,BC=8,则EF的长是 ( )
A.2 B.2.5 C.5 D.10
9.菱形的一条对角线长为8,另一条对角线长是方程x2-4x-12=0的一个根,则菱形的边长是 ( )
A.10 B.8 C.6 D.5
10.如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E,F分别在BC和CD上,下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④正方形对角线AC=1+.其中正确的是 ( )
A.①② B.①②④ C.②③④ D.①③④
二、填空题(本题共6小题,每小题3分,共18分)
11.若实数x满足方程(x+2)(x-5)=0,则x的值为 .
12.已知关于x的方程x2-(2m+5)x+3=0的一个解为x=-1,则该方程的另一根为 .
13.在 ABCD中,对角线AC,BD相交于点O,请添加一个条件 ,使其成为菱形.(添加一个即可)
14.关于x的一元二次方程(k-1)x2-(k-1)x+=0有两个相等的实数根,则k的值为 .
15.对于实数a,b,定义运算“※”如下:a※b=a2-ab.例如:4※3=42-4×3=4.若(x+1)※(3x-2)=0,则x的值为 .
16.如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE=AB.将△BEF沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q.对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确结论的序号是 .
三、解答题(本大题共9小题,共72分)
17.(6分)解方程:x(x+2)=3x+6.
18.(6分)如图,矩形ABCD的对角线AC=8,∠AOB=60°,求BC的长.
19.(6分)如图①,某校进行校园改造,准备将一块正方形空地划出部分区域栽种鲜花,原空地一边减少了4 m,另一边减少了5 m,剩余部分面积为650 m2.求原正方形空地的边长.
20.(6分)如图,在正方形ABCD中,点E是BC上一点,点F是CD的延长线上的一点,且BE=DF,判断△AEF的形状,并说明理由.
21.(8分)已知关于x的一元二次方程x2-2x-k-2=0有两个不相等的实数根.
(1)求k的取值范围.
(2)给k取一个负整数值,解这个方程.
22.(8分)已知一元二次方程x2+ax+b=0的一个解是x=2,另一个解也是正数,而且是方程(x+4)2=3x+52的解,求a和b的值.
23.(10分)如图,已知菱形ABCD的对角线AC,BD相交于点O,分别过点A,D作AO,DO的垂线,两垂线交于点E.
(1)请判断四边形AODE的形状并给出证明.
(2)若四边形AODE的面积为12,点G是四边形AODE对角线AD的中点,且EG=,请计算四边形AODE的周长.
24.(10分)阅读下列材料,完成文后任务:
我们知道,a2+2ab+b2或a2-2ab+b2都称为完全平方式,通常把一个二项式加上某一项后使之成为完全平方式的方法称为配方法,利用配方法不仅可以解一元二次方程,还有其他方面的应用. 例如:若m2+2m+n2-4n+5=0,求m和n的值. 解:由已知得,m2+2m+1+n2-4n+4=0,∴(m+1)2+(n-2)2=0, ∴m+1=0,n-2=0,∴m=-1,n=2. 又如:求代数式y2+6y+1的最小值. 解:y2+6y+1=y2+6y+9-8=(y+3)2-8, ∵(y+3)2≥0,∴(y+3)2-8≥-8, ∴代数式y2+6y+1的最小值为-8.
任务:(1)已知x2+5y2-4xy+2y+1=0,求x和y的值.
(2)求代数式m2+m+2的最小值.
(3)某居民小区要在一块一边靠墙(墙长15米)的空地上建一个矩形花园ABCD,花园一边靠墙,另三边用总长为20米的栅栏围成,如图所示.设AB=x米,请问,当x取何值时,花园的面积最大 最大面积是多少平方米
25.(12分)某数学兴趣小组在数学课外活动中,研究三角形和正方形的性质时,做了如下探究:在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作正方形ADEF,连接CF.
(1)观察猜想
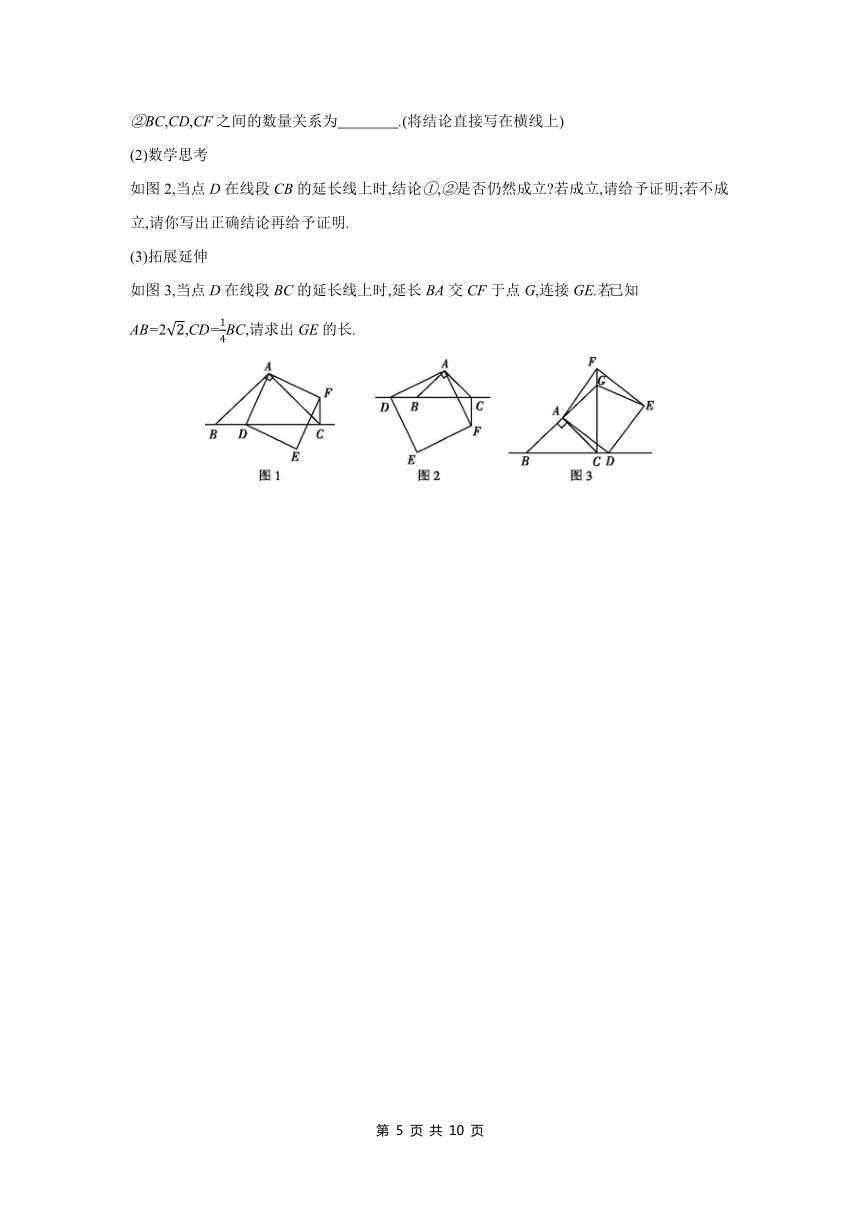
如图1,当点D在线段BC上时,
①BC与CF的位置关系为 ;
②BC,CD,CF之间的数量关系为 .(将结论直接写在横线上)
(2)数学思考
如图2,当点D在线段CB的延长线上时,结论①,②是否仍然成立 若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
(3)拓展延伸
如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE.若已知AB=2,CD=BC,请求出GE的长.
参考答案
一、选择题
1 2 3 4 5 6 7 8 9 10
B A C A A D D B D B
1.B 【解析】A选项不含二次项,C选项含有两个未知数,D选项含有分式,它们都不是一元二次方程,只有B选项符合.
2.A 【解析】∵Δ=b2-4ac=12-4×2×(-1)=9>0,∴方程有两个不相等的实数根.
3.C 【解析】对角线相等的平行四边形是矩形,所以A选项错误;对角线互相垂直的平行四边形是菱形,所以B选项错误;一组对边平行且相等的四边形是平行四边形,所以D选项错误.
4.A 【解析】把x=2代入方程,得22+5×2-m=0,∴m=14.因此原方程为x2+5x-14=0,解得x=2或x=-7.
5.A 【解析】 x2-x=,x2-x+=+,(x-)2=.
6.D 【解析】无盖纸盒底面长为(40-2x) cm,宽为(30-2x) cm,∴底面积为(40-2x)(30-2x) cm2.因此(30-2x)(40-2x)=600.
7.D 【解析】由菱形的性质可知OB==2,所以S菱形ABCD=AC·BD=×2×4=4.
8.B 【解析】∵四边形ABCD是矩形,∴∠ABC=90°.又∵AB=6,BC=8,∴AC=BD=10,∴OD=BD=5.∵E,F分别是AO,AD的中点,∴EF=OD=2.5.
9.D 【解析】解方程x2-4x-12=0得x=6或x=-2(舍去),即另一条对角线长是6.由菱形的两条对角线互相垂直平分性质结合勾股定理即可求得边长为5.
10.B 【解析】∵四边形ABCD是正方形,∴AB=BC=CD=AD,∠B=∠D=∠BAD=90°.∵△AEF是等边三角形,∴∠EAF=60°,AE=AF=EF.∴Rt△ABE≌Rt△ADF(HL),∴BE=DF,∠BAE=∠DAF=(∠BAD-∠EAF)=15°,∴BC-BE=CD-DF,即CE=CF,∠AEB=75°,①②正确;BE+DF显然≠EF,③错误;∵△AEF是边长为2的等边三角形,连接AC,交EF于点G,∴AC⊥EF,∴AG=,CG=EG=1,AC=AG+GC=1+,∴④正确.
二、填空题
11 12 13 14 15 16
-2 或5 -3 AB=AD(答案不唯一) 2 -1或 ①④
11.-2或5 【解析】∵(x+2)(x-5)=0,∴x+2=0或x-5=0,∴x=-2或x=5.
12.-3
13.AB=AD(答案不唯一)
14.2 【解析】由题意,得
,解得k=2.
15.-1或 【解析】由题意,得(x+1)2-(x+1)(3x-2)=0,解得x1=-1,x2=.
16.①④ 【解析】∵AE=AB,∴BE=2AE,由折叠的性质得PE=BE=2AE,∴∠APE=30°,∴∠AEP=90°-30°=60°,∴∠BEF=(180°-∠AEP)=×(180°-60°)=60°,∴∠EFB=90°-60°=30°,∴EF=2BE,故①正确;∵BE=PE,∴EF=2PE,∵EF>PF,∴2PE>PF,故②错误;由折叠可知EF⊥PB,∴∠EBQ=∠EFB=30°,∴BE=2EQ.∵EF=2BE,∴EF=4EQ,FQ=3EQ,故③错误;由折叠的性质知BF=PF,∠EFB=∠EFP=30°,∴∠BFP=30°+30°=60°,∴△PBF是等边三角形,故④正确.综上所述,正确结论的序号是①④.
三、解答题
17.解:方程可变形为x(x+2)-3(x+2)=0,
∴(x+2)(x-3)=0,(3分)
∴x+2=0,x-3=0,
∴x1=-2,x2=3.(6分)
18.解:∵四边形ABCD是矩形,∴∠ABC=90°,OA=OC=AC=BD=OD=OB=4.(1分)
∵∠AOB=60°,∴△AOB是等边三角形.
∴OA=OB=AB=4.(4分)
在Rt△ABC中,由勾股定理,得BC===4.(6分)
19.解:设原正方形空地的边长为x m,则剩余部分长为(x-4)m,宽为(x-5)m,
依题意得(x-4)(x-5)=650,(3分)
整理得x2-9x-630=0,
解得x1=30,x2=-21(不合题意,舍去).
答:原正方形空地的边长为30 m.(6分)
20.解:△AEF是等腰直角三角形.(1分)
理由如下:
∵四边形ABCD是正方形,∴AB=AD,∠B=∠ADC=90°,
∴∠ADF=90°,∴∠B=∠ADF=∠BAD=90°,
在△ABE和△ADF中,AB=AD,∠B=∠ADF,BE=DF,
∴△ABE≌△ADF(SAS),(4分)
∴∠BAE=∠DAF,AE=AF.
∵∠BAD=90°,∴∠EAF=∠EAD+∠DAF=∠EAD+∠BAE=90°,即∠EAF=90°.∴△AEF是等腰直角三角形.(6分)
21.解:∵方程有两个不相等的实数根,
∴Δ=(-2)2-4×1×(-k-2)>0,解得k>-3.(4分)
(2)答案不唯一,合理即可.
取k=-2,则方程变形为x2-2x=0.
解得x1=0,x2=2.(8分)
22.解:解方程(x+4)2=3x+52,得x1=4,x2=-9.(2分)
∵一元二次方程x2+ax+b=0的另一个解也是正数,而且是方程(x+4)2=3x+52的解,
∴一元二次方程x2+ax+b=0的另一个根是x=4.
∴42+4a+b=0,即4a+b=-16.①(5分)
又x=2是一元二次方程x2+ax+b=0的根,所以22+2a+b=0,即2a+b=-4.②
由①②联立方程组解得a=-6,b=8.(8分)
23.解:(1)四边形AODE是矩形.证明如下:
∵四边形ABCD是菱形,∴AC⊥BD,∴∠AOD=90°.
∵AE⊥AO,DE⊥DO,∴∠OAE=∠ODE=90°,
∴四边形AODE是矩形.(5分)
(2)由(1)知四边形AODE是矩形,∴∠AED=90°.
在Rt△ADE中,∵点G是斜边AD的中点,EG=,∴AD=2GE=5.
由勾股定理,知AE2+DE2=AD2=52=25,
∴(AE+DE)2-2AE·DE=25.
∵矩形AODE的面积为12,即AE·DE=12,
∴(AE+DE)2-2×12=25,∴AE+DE=7,
∴四边形AODE的周长=2(AE+DE)=14.(10分)
24.解:(1)∵x2+5y2-4xy+2y+1=0,
∴x2-4xy+4y2+y2+2y+1=0,
∴(x-2y)2+(y+1)2=0,
∴x-2y=0,y+1=0,
∴x=-2,y=-1 .(3分)
(2)m2+m+2=m2+m++=(m+)2+,
∵(m+)2≥0,∴(m+)2+≥,
∴m2+m+2的最小值为.(7分)
(3)∵AB=x米,∴CD=x米,
∵AB+BC+DC=20,
∴BC=(20-2x)米,
∴花园的面积S=AB·BC=x(20-2x)=-2x2+20x=-2(x2-10x+25)+50=-2(x-5)2+50,
∵-2(x-5)2≤0,∴-2(x-5)2+50≤50,
∴当x=5时,花园的面积最大,最大面积是50平方米.(10分)
25.解:(1)①垂直;②BC=CD+CF.(2分)
(2)①成立,②不成立,正确结论是BC=DC-CF.(4分)
证明如下:
∵四边形ADEF是正方形,∴AD=AF,∠DAF=90°.
∵∠BAC=90°,∴∠DAB=∠FAC.
又∵AD=AF,AB=AC,∴△DAB≌△FAC.
∴DB=CF,∠DBA=∠FCA.
∵∠BAC=90°,AB=AC,∴∠ABC=∠ACB=45°,
∴∠FCA=∠DBA=135°,∴∠BCF=90°,∴BC⊥CF.
∵BC=DC-DB,DB=CF,∴BC=DC-CF.(7分)
(3)如图,过点A作AM⊥BC于点M,过点E作EN⊥BC于点N,EP⊥CF于点P,易得四边形PCNE为矩形.
∵∠BAC=90°,AB=AC=2,∴BC=4,AM=BM=CM=2.
∵CD=BC,∴CD=1,∴MD=3.
∵∠ADC+∠EDN=90°,∠EDN+∠DEN=90°,∴∠ADC=∠DEN.
又∵∠AMD=∠DNE=90°,AD=DE,
∴△AMD≌△DNE,∴DN=AM=2,EN=MD=3.
∵CG=BC=4,∴GP=4-3=1.
在Rt△GPE中,由勾股定理,得GE===.(12分)
时间:90分钟 满分:120分 考试范围:1.1~2.4
一、选择题(本题共10小题,每小题3分,共30分)
1.下列方程中,一定是关于x的一元二次方程的是 ( )
A.x2-x(x-1)=0 B.x2+x-2=0
C.x2-2y+1=0 D.x2-=1
2.一元二次方程2x2-x-1=0的根的情况是 ( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.只有一个实数根 D.没有实数根
3.下列命题中正确的是 ( )
A.对角线相等的四边形是矩形
B.对角线互相垂直的四边形是菱形
C.对角线互相垂直平分且相等的四边形是正方形
D.一组对边相等,另一组对边平行的四边形是平行四边形
4.已知关于x的一元二次方程x2+5x-m=0的一个根是2,则另一个根是 ( )
A.-7 B.7 C.3 D.-3
5.用配方法解一元二次方程2x2-3x-1=0,配方正确的是 ( )
A.(x-)2= B.(x-)2=
C.(x-)2= D.(x-)2=
6.如图,把一块长为40 cm,宽为30 cm的矩形硬纸板的四角剪去四个相同小正方形,然后把纸板的四边沿虚线折起,并用胶带粘好,即可做成一个无盖纸盒.若该无盖纸盒的底面积为600 cm2,设剪去的小正方形的边长为x cm,则下列方程正确的是 ( )
A.(30-2x)(40-x)=600 B.(30-x)(40-x)=600
C.(30-x)(40-2x)=600 D.(30-2x)(40-2x)=600
7.菱形ABCD的边长为,对角线AC,BD交于点O,OA=1,则菱形ABCD的面积为 ( )
A. B.2 C.2 D.4
8.在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别是AO,AD的中点,连接EF,若AB=6,BC=8,则EF的长是 ( )
A.2 B.2.5 C.5 D.10
9.菱形的一条对角线长为8,另一条对角线长是方程x2-4x-12=0的一个根,则菱形的边长是 ( )
A.10 B.8 C.6 D.5
10.如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E,F分别在BC和CD上,下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④正方形对角线AC=1+.其中正确的是 ( )
A.①② B.①②④ C.②③④ D.①③④
二、填空题(本题共6小题,每小题3分,共18分)
11.若实数x满足方程(x+2)(x-5)=0,则x的值为 .
12.已知关于x的方程x2-(2m+5)x+3=0的一个解为x=-1,则该方程的另一根为 .
13.在 ABCD中,对角线AC,BD相交于点O,请添加一个条件 ,使其成为菱形.(添加一个即可)
14.关于x的一元二次方程(k-1)x2-(k-1)x+=0有两个相等的实数根,则k的值为 .
15.对于实数a,b,定义运算“※”如下:a※b=a2-ab.例如:4※3=42-4×3=4.若(x+1)※(3x-2)=0,则x的值为 .
16.如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE=AB.将△BEF沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q.对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确结论的序号是 .
三、解答题(本大题共9小题,共72分)
17.(6分)解方程:x(x+2)=3x+6.
18.(6分)如图,矩形ABCD的对角线AC=8,∠AOB=60°,求BC的长.
19.(6分)如图①,某校进行校园改造,准备将一块正方形空地划出部分区域栽种鲜花,原空地一边减少了4 m,另一边减少了5 m,剩余部分面积为650 m2.求原正方形空地的边长.
20.(6分)如图,在正方形ABCD中,点E是BC上一点,点F是CD的延长线上的一点,且BE=DF,判断△AEF的形状,并说明理由.
21.(8分)已知关于x的一元二次方程x2-2x-k-2=0有两个不相等的实数根.
(1)求k的取值范围.
(2)给k取一个负整数值,解这个方程.
22.(8分)已知一元二次方程x2+ax+b=0的一个解是x=2,另一个解也是正数,而且是方程(x+4)2=3x+52的解,求a和b的值.
23.(10分)如图,已知菱形ABCD的对角线AC,BD相交于点O,分别过点A,D作AO,DO的垂线,两垂线交于点E.
(1)请判断四边形AODE的形状并给出证明.
(2)若四边形AODE的面积为12,点G是四边形AODE对角线AD的中点,且EG=,请计算四边形AODE的周长.
24.(10分)阅读下列材料,完成文后任务:
我们知道,a2+2ab+b2或a2-2ab+b2都称为完全平方式,通常把一个二项式加上某一项后使之成为完全平方式的方法称为配方法,利用配方法不仅可以解一元二次方程,还有其他方面的应用. 例如:若m2+2m+n2-4n+5=0,求m和n的值. 解:由已知得,m2+2m+1+n2-4n+4=0,∴(m+1)2+(n-2)2=0, ∴m+1=0,n-2=0,∴m=-1,n=2. 又如:求代数式y2+6y+1的最小值. 解:y2+6y+1=y2+6y+9-8=(y+3)2-8, ∵(y+3)2≥0,∴(y+3)2-8≥-8, ∴代数式y2+6y+1的最小值为-8.
任务:(1)已知x2+5y2-4xy+2y+1=0,求x和y的值.
(2)求代数式m2+m+2的最小值.
(3)某居民小区要在一块一边靠墙(墙长15米)的空地上建一个矩形花园ABCD,花园一边靠墙,另三边用总长为20米的栅栏围成,如图所示.设AB=x米,请问,当x取何值时,花园的面积最大 最大面积是多少平方米
25.(12分)某数学兴趣小组在数学课外活动中,研究三角形和正方形的性质时,做了如下探究:在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作正方形ADEF,连接CF.
(1)观察猜想
如图1,当点D在线段BC上时,
①BC与CF的位置关系为 ;
②BC,CD,CF之间的数量关系为 .(将结论直接写在横线上)
(2)数学思考
如图2,当点D在线段CB的延长线上时,结论①,②是否仍然成立 若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
(3)拓展延伸
如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE.若已知AB=2,CD=BC,请求出GE的长.
参考答案
一、选择题
1 2 3 4 5 6 7 8 9 10
B A C A A D D B D B
1.B 【解析】A选项不含二次项,C选项含有两个未知数,D选项含有分式,它们都不是一元二次方程,只有B选项符合.
2.A 【解析】∵Δ=b2-4ac=12-4×2×(-1)=9>0,∴方程有两个不相等的实数根.
3.C 【解析】对角线相等的平行四边形是矩形,所以A选项错误;对角线互相垂直的平行四边形是菱形,所以B选项错误;一组对边平行且相等的四边形是平行四边形,所以D选项错误.
4.A 【解析】把x=2代入方程,得22+5×2-m=0,∴m=14.因此原方程为x2+5x-14=0,解得x=2或x=-7.
5.A 【解析】 x2-x=,x2-x+=+,(x-)2=.
6.D 【解析】无盖纸盒底面长为(40-2x) cm,宽为(30-2x) cm,∴底面积为(40-2x)(30-2x) cm2.因此(30-2x)(40-2x)=600.
7.D 【解析】由菱形的性质可知OB==2,所以S菱形ABCD=AC·BD=×2×4=4.
8.B 【解析】∵四边形ABCD是矩形,∴∠ABC=90°.又∵AB=6,BC=8,∴AC=BD=10,∴OD=BD=5.∵E,F分别是AO,AD的中点,∴EF=OD=2.5.
9.D 【解析】解方程x2-4x-12=0得x=6或x=-2(舍去),即另一条对角线长是6.由菱形的两条对角线互相垂直平分性质结合勾股定理即可求得边长为5.
10.B 【解析】∵四边形ABCD是正方形,∴AB=BC=CD=AD,∠B=∠D=∠BAD=90°.∵△AEF是等边三角形,∴∠EAF=60°,AE=AF=EF.∴Rt△ABE≌Rt△ADF(HL),∴BE=DF,∠BAE=∠DAF=(∠BAD-∠EAF)=15°,∴BC-BE=CD-DF,即CE=CF,∠AEB=75°,①②正确;BE+DF显然≠EF,③错误;∵△AEF是边长为2的等边三角形,连接AC,交EF于点G,∴AC⊥EF,∴AG=,CG=EG=1,AC=AG+GC=1+,∴④正确.
二、填空题
11 12 13 14 15 16
-2 或5 -3 AB=AD(答案不唯一) 2 -1或 ①④
11.-2或5 【解析】∵(x+2)(x-5)=0,∴x+2=0或x-5=0,∴x=-2或x=5.
12.-3
13.AB=AD(答案不唯一)
14.2 【解析】由题意,得
,解得k=2.
15.-1或 【解析】由题意,得(x+1)2-(x+1)(3x-2)=0,解得x1=-1,x2=.
16.①④ 【解析】∵AE=AB,∴BE=2AE,由折叠的性质得PE=BE=2AE,∴∠APE=30°,∴∠AEP=90°-30°=60°,∴∠BEF=(180°-∠AEP)=×(180°-60°)=60°,∴∠EFB=90°-60°=30°,∴EF=2BE,故①正确;∵BE=PE,∴EF=2PE,∵EF>PF,∴2PE>PF,故②错误;由折叠可知EF⊥PB,∴∠EBQ=∠EFB=30°,∴BE=2EQ.∵EF=2BE,∴EF=4EQ,FQ=3EQ,故③错误;由折叠的性质知BF=PF,∠EFB=∠EFP=30°,∴∠BFP=30°+30°=60°,∴△PBF是等边三角形,故④正确.综上所述,正确结论的序号是①④.
三、解答题
17.解:方程可变形为x(x+2)-3(x+2)=0,
∴(x+2)(x-3)=0,(3分)
∴x+2=0,x-3=0,
∴x1=-2,x2=3.(6分)
18.解:∵四边形ABCD是矩形,∴∠ABC=90°,OA=OC=AC=BD=OD=OB=4.(1分)
∵∠AOB=60°,∴△AOB是等边三角形.
∴OA=OB=AB=4.(4分)
在Rt△ABC中,由勾股定理,得BC===4.(6分)
19.解:设原正方形空地的边长为x m,则剩余部分长为(x-4)m,宽为(x-5)m,
依题意得(x-4)(x-5)=650,(3分)
整理得x2-9x-630=0,
解得x1=30,x2=-21(不合题意,舍去).
答:原正方形空地的边长为30 m.(6分)
20.解:△AEF是等腰直角三角形.(1分)
理由如下:
∵四边形ABCD是正方形,∴AB=AD,∠B=∠ADC=90°,
∴∠ADF=90°,∴∠B=∠ADF=∠BAD=90°,
在△ABE和△ADF中,AB=AD,∠B=∠ADF,BE=DF,
∴△ABE≌△ADF(SAS),(4分)
∴∠BAE=∠DAF,AE=AF.
∵∠BAD=90°,∴∠EAF=∠EAD+∠DAF=∠EAD+∠BAE=90°,即∠EAF=90°.∴△AEF是等腰直角三角形.(6分)
21.解:∵方程有两个不相等的实数根,
∴Δ=(-2)2-4×1×(-k-2)>0,解得k>-3.(4分)
(2)答案不唯一,合理即可.
取k=-2,则方程变形为x2-2x=0.
解得x1=0,x2=2.(8分)
22.解:解方程(x+4)2=3x+52,得x1=4,x2=-9.(2分)
∵一元二次方程x2+ax+b=0的另一个解也是正数,而且是方程(x+4)2=3x+52的解,
∴一元二次方程x2+ax+b=0的另一个根是x=4.
∴42+4a+b=0,即4a+b=-16.①(5分)
又x=2是一元二次方程x2+ax+b=0的根,所以22+2a+b=0,即2a+b=-4.②
由①②联立方程组解得a=-6,b=8.(8分)
23.解:(1)四边形AODE是矩形.证明如下:
∵四边形ABCD是菱形,∴AC⊥BD,∴∠AOD=90°.
∵AE⊥AO,DE⊥DO,∴∠OAE=∠ODE=90°,
∴四边形AODE是矩形.(5分)
(2)由(1)知四边形AODE是矩形,∴∠AED=90°.
在Rt△ADE中,∵点G是斜边AD的中点,EG=,∴AD=2GE=5.
由勾股定理,知AE2+DE2=AD2=52=25,
∴(AE+DE)2-2AE·DE=25.
∵矩形AODE的面积为12,即AE·DE=12,
∴(AE+DE)2-2×12=25,∴AE+DE=7,
∴四边形AODE的周长=2(AE+DE)=14.(10分)
24.解:(1)∵x2+5y2-4xy+2y+1=0,
∴x2-4xy+4y2+y2+2y+1=0,
∴(x-2y)2+(y+1)2=0,
∴x-2y=0,y+1=0,
∴x=-2,y=-1 .(3分)
(2)m2+m+2=m2+m++=(m+)2+,
∵(m+)2≥0,∴(m+)2+≥,
∴m2+m+2的最小值为.(7分)
(3)∵AB=x米,∴CD=x米,
∵AB+BC+DC=20,
∴BC=(20-2x)米,
∴花园的面积S=AB·BC=x(20-2x)=-2x2+20x=-2(x2-10x+25)+50=-2(x-5)2+50,
∵-2(x-5)2≤0,∴-2(x-5)2+50≤50,
∴当x=5时,花园的面积最大,最大面积是50平方米.(10分)
25.解:(1)①垂直;②BC=CD+CF.(2分)
(2)①成立,②不成立,正确结论是BC=DC-CF.(4分)
证明如下:
∵四边形ADEF是正方形,∴AD=AF,∠DAF=90°.
∵∠BAC=90°,∴∠DAB=∠FAC.
又∵AD=AF,AB=AC,∴△DAB≌△FAC.
∴DB=CF,∠DBA=∠FCA.
∵∠BAC=90°,AB=AC,∴∠ABC=∠ACB=45°,
∴∠FCA=∠DBA=135°,∴∠BCF=90°,∴BC⊥CF.
∵BC=DC-DB,DB=CF,∴BC=DC-CF.(7分)
(3)如图,过点A作AM⊥BC于点M,过点E作EN⊥BC于点N,EP⊥CF于点P,易得四边形PCNE为矩形.
∵∠BAC=90°,AB=AC=2,∴BC=4,AM=BM=CM=2.
∵CD=BC,∴CD=1,∴MD=3.
∵∠ADC+∠EDN=90°,∠EDN+∠DEN=90°,∴∠ADC=∠DEN.
又∵∠AMD=∠DNE=90°,AD=DE,
∴△AMD≌△DNE,∴DN=AM=2,EN=MD=3.
∵CG=BC=4,∴GP=4-3=1.
在Rt△GPE中,由勾股定理,得GE===.(12分)
同课章节目录
