2024-2025北师大版九年级数学上册全部月考闯关测试卷(二)(含详解)
文档属性
| 名称 | 2024-2025北师大版九年级数学上册全部月考闯关测试卷(二)(含详解) |
|
|
| 格式 | docx | ||
| 文件大小 | 288.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 16:02:53 | ||
图片预览

文档简介
月考测试卷(二)
时间:90分钟 满分:120分 考试范围:上册全部
一、选择题(本题共10小题,每小题3分,共30分)
1.下列线段中,能成比例的是 ( )
A.3 cm,4 cm,5 cm,6 cm B.3 cm,5 cm,6 cm,9 cm
C.3 cm,6 cm,7 cm,10 cm D.3 cm,6 cm,7 cm,14 cm
2.如图,一个圆柱体被截去一部分,则该几何体的主视图是 ( )
3.若关于x的一元二次方程x2-mx+2=0的一个根是1,则m的值是 ( )
A.1 B.2 C.3 D.4
4.下列各点在反比例函数y=-的图象上的是 ( )
A.(-1,-2021) B.(1,2021)
C.(-1,) D.(,-)
5.如图,夜晚路灯下有一排同样高的旗杆,离路灯越近,旗杆的影子 ( )
A.越长 B.越短
C.一样长 D.随时间变化而变化
6.如图,在菱形ABOC中,AB=2,∠A=60°,菱形的一个顶点C在反比例函数y=(k≠0)的图象上,则反比例函数的解析式为 ( )
A.y=- B.y=-
C.y=- D.y=
7.从马航、张斌、王浩、李敏四人中抽调两人参加“寸草心”志愿服务队,恰好抽到马航和李敏的概率是 ( )
A. B. C. D.
8.已知x1,x2是方程x2-2x-7=0的两根,则-x1+x2的值为 ( )
A.9 B.7 C.5 D.3
9.如图,矩形ABCD的四个顶点分别在直线l3,l4,l2,l1上.若直线l1∥l2∥l3∥l4且间距相等,CB交直线l3于点G,AB=4,BC=3,则的值为 ( )
A. B. C. D.
10.如图,在矩形ABCD中,AC,BD相交于点O,过点B作BF⊥AC交CD于点F,交AC于点M,过点D作DE∥BF交AB于点E,交AC于点N,连接FN,EM.则下列结论:①DN=BM;②EM∥FN;③AE=FC;④当AO=AD时,四边形DEBF是菱形.其中,正确结论的个数是 ( )
A.1 B.2 C.3 D.4
二、填空题(本题共6小题,每小题3分,共18分)
11.同一时刻,小明在阳光下的影长为2米,与他邻近的旗杆的影长为6米,小明的身高为1.6米,则旗杆的高为 米.
12.菱形的一条对角线长为8,其边长是方程x2-9x+20=0的一个根,则该菱形的周长为 .
13.一个圆柱的三视图如图所示,若其俯视图为圆,则这个圆柱的体积为 .
14.如图,在正方形ABCD中,已知点E是AD的中点,点F是CD上一点,且DF=CD,连接EF,BE,若BE=4,则EF= .
15.如图,某人与一座建筑物DE的距离AF=120 m,他站在A处,将自己的食指竖直举在右眼前,闭上左眼,将食指前后移动,使食指恰好将该建筑物遮住,若此时眼睛到食指的距离AG约为40 cm,食指的长约8 cm,则该建筑物的高度约是 m.
16.如图,已知直线y=mx+4分别与y轴,x轴交于A,B两点,且△ABO的面积为16,反比例函数的图象恰好经过AB的中点,则反比例函数的表达式为 .
三、解答题(本大题共9小题,共72分)
17.(6分)解方程:x(x-2)=2-x.
18.(6分)如图,当太阳光与地面上的树影成45°角时,树影投射在墙上的影高CD等于2米,若树根到墙的距离BC等于8米,试求树高AB.
19.(6分)如图,在四边形ABCD中,AB∥CD,AB=AD,AC平分∠BAD.求证:四边形ABCD是菱形.
20.(6分)如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,CD⊥AB,垂足为D,E为BC的中点,AE与CD交于点F,求DF的长.
21.(8分)乒乓球是我国的国球,比赛采用单局11分制,是一种世界流行的球类体育项目,比赛分团体、单打、双打等数种.在某站公开赛中,某直播平台同时直播4场男单四分之一比赛,四场比赛的球桌号分别为“T1”“T2”“T3”“T4”(假设4场比赛同时开始),小宁和父亲准备一同观看其中的某一场比赛,但两人的意见不统一,于是采用抽签的方式决定,抽签规则如下:将正面分别写有数字“1”“2”“3”“4”的四张卡片(除数字不同外,其余均相同),数字“1”“2”“3”“4”分别对应球桌号“T1”“T2”“T3”“T4”,背面朝上洗匀,父亲先从中随机抽取一张,小宁再从剩下的3张卡片中随机抽取一张,比较两人所抽卡片上的数字,观看较大的数字对应球桌的比赛.
(1)下列事件中属于必然事件的是 .
A.抽到的是小宁最终想要看的一场比赛的球桌号
B.抽到的是父亲最终想要看的一场比赛的球桌号
C.小宁和父亲抽到同一个球桌号
D.小宁和父亲抽到的球桌号不一样
(2)用列表法或画树状图法求小宁和父亲最终观看“T4”球桌比赛的概率.
22.(8分)如图,一次函数y=x+1的图象与反比例函数y=的图象相交于A(2,m)和B两点.
(1)求反比例函数的解析式;
(2)求点B的坐标.
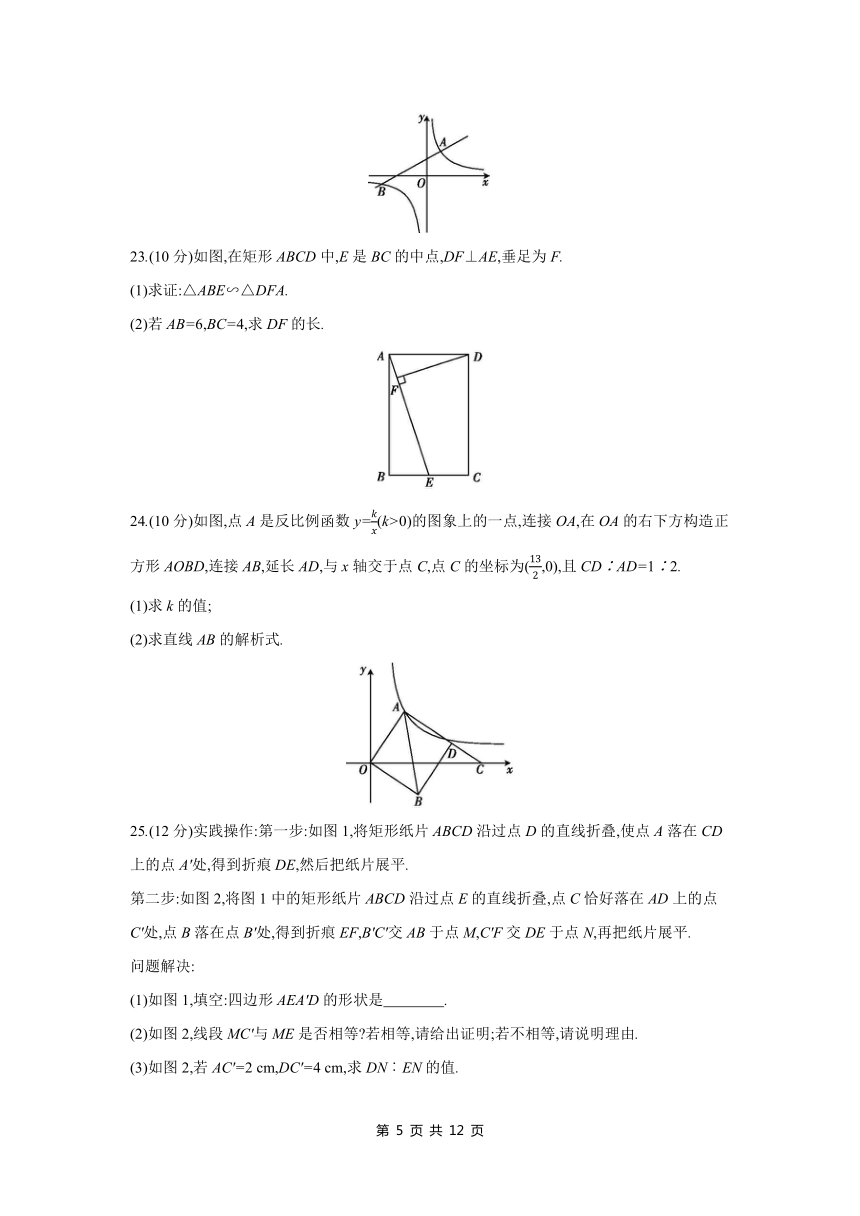
23.(10分)如图,在矩形ABCD中,E是BC的中点,DF⊥AE,垂足为F.
(1)求证:△ABE∽△DFA.
(2)若AB=6,BC=4,求DF的长.
24.(10分)如图,点A是反比例函数y=(k>0)的图象上的一点,连接OA,在OA的右下方构造正方形AOBD,连接AB,延长AD,与x轴交于点C,点C的坐标为(,0),且CD∶AD=1∶2.
(1)求k的值;
(2)求直线AB的解析式.
25.(12分)实践操作:第一步:如图1,将矩形纸片ABCD沿过点D的直线折叠,使点A落在CD上的点A'处,得到折痕DE,然后把纸片展平.
第二步:如图2,将图1中的矩形纸片ABCD沿过点E的直线折叠,点C恰好落在AD上的点C'处,点B落在点B'处,得到折痕EF,B'C'交AB于点M,C'F交DE于点N,再把纸片展平.
问题解决:
(1)如图1,填空:四边形AEA'D的形状是 .
(2)如图2,线段MC'与ME是否相等 若相等,请给出证明;若不相等,请说明理由.
(3)如图2,若AC'=2 cm,DC'=4 cm,求DN︰EN的值.
参考答案
一、选择题
1 2 3 4 5 6 7 8 9 10
D C C D B B C A A D
1.D 【解析】通过计算可知,只有3 cm,6 cm,7 cm,14 cm四条线段能成比例.
2.C 【解析】从正面看是一个右上角截去一角的矩形.
3.C 【解析】将x=1代入方程x2-mx+2=0中即可解得m=3.
4.D 【解析】将各个选项中的点的坐标分别代入关系式验证,即可知应选D.
5.B 【解析】由图易得AB6.B 【解析】因为∠A=60°,OC=2,∠COB=60°,如图,过点C作CD⊥OB于点D,则OD=1,CD=,因为点C在第二象限,所以点C的坐标为(-1,),因为顶点C在反比例函数y=的图象上,所以k=-1×=-,所以反比例函数的解析式为y=-.
7.C 【解析】列表如下,观察表格可知,总共有12种等可能的结果,符合要求的有2种,
马航 张斌 王浩 李敏
马航 (马航,张斌) (马航,王浩) (马航,李敏)
张斌 (张斌,马航) (张斌,王浩) (张斌,李敏)
王浩 (王浩,马航) (王浩,张斌) (王浩,李敏)
李敏 (李敏,马航) (李敏,张斌) (李敏,王浩)
所以恰好抽到马航和李敏的概率P==.
8.A 【解析】根据题意得x1+x2=2,-2x1-7=0,∴-2x1=7.∴-x1+x2=-2x1+x1+x2=7+2=9.
9.A 【解析】如图,作CF⊥l4于点F,交l3于点E.由已知可得,GE∥BF,CE=EF,∵BC=3,∴GB=.∵四边形ABCD是矩形,AB=4,∴CD=AB=4,∴===.
10.D 【解析】∵四边形ABCD是矩形,∴AB=CD,AD=BC,AD∥BC,∴∠DAN=∠BCM.∵BF⊥AC,DE∥BF,∴DE⊥AC,即∠AND=∠CMB=90°,∴△ADN≌△CBM,∴DN=BM,∠ADN=∠CBM,则△ADE≌△CBF,∴AE=FC,DE=BF,∴NE=MF,∴四边形EMFN是平行四边形,∴EM∥FN,即①②③都是正确的.由AE=CF,AB=CD,∴BE=DF,∴四边形DEBF是平行四边形.∵四边形ABCD是矩形,∴AO=DO.∵当AO=AD时,AO=DO=AD,∴△ADO是等边三角形,∴∠ADN=∠BDE=30°,∴∠BDE=∠ABD=30°,∴DE=BE,∴四边形DEBF是菱形,则④也是正确的.
二、填空题
11 12 13 14 15 16
4.8 20 24π 2 24 y=
11.4.8 【解析】设旗杆的高为x米,则有=,解得x=4.8.
12.20 【解析】解方程得x=4或x=5,分两种情况:①当AB=AD=4时,4+4=8,不能构成三角形;②当AB=AD=5时,5+5>8,即可得出菱形ABCD的周长为5×4=20.
13.24π 【解析】π()2×6=24π.
14.2 【解析】∵四边形ABCD是正方形,∴AB=BC=CD=AD,∠A=∠D=90°,∵点E是AD的中点,∴AE=DE=AD,∵DF=CD,∴DF=AD=×2AE=AE,在△ABE和△DEF中,==2,∠A=∠D,∴△ABE∽△DEF,∴==2.EF==2.
15.24 【解析】∵40 cm=0.4 m,8 cm=0.08 m,BC∥DE,AG⊥BC,AF⊥DE,∴△ABC∽△ADE,∴BC∶DE=AG∶AF,∴0.08∶DE=0.4∶120,∴DE=24 m.
16.y= 【解析】由题意可得A(0,4),△ABO的面积为16,∴OB=8,即B(8,0),∴AB的中点坐标为(4,2),设反比例函数的表达式为y=,得k=4×2=8,∴反比例函数的表达式为y=.
三、解答题
17.解:移项得x(x-2)+(x-2)=0,
方程左边提公因式得(x-2)(x+1)=0,即x-2=0或x+1=0,
∴x1=2,x2=-1.(6分)
18.解:如图,过点D作DH⊥AB于点H,则DH=CB=8米.
在Rt△ADH中,∵∠ADH=45°,∴∠DAB=45°,∴AH=DH=8.
∴AB=AH+HB=8+2=10.
即树高AB等于10米.(6分)
19.证明:∵AB∥CD,∴∠BAC=∠DCA,
∵AC平分∠BAD,∴∠DAC=∠BAC,∴∠DAC=∠DCA,∴AD=CD,
∵AB=AD,∴AB=CD,
∵AB∥CD,∴四边形ABCD是平行四边形.
∵AB=AD,∴四边形ABCD是菱形.(6分)
20.解:∵∠ACB=90°,AC=3,BC=4,由勾股定理得AB=5,
∵CD⊥AB,∴AC·BC=AB·CD,∴CD=.
由勾股定理得AD=,BD=.(3分)
过点E作EG∥AB交CD于点G,DG=CD=,EG=BD=,
∵=,∴=,∴DF=.(6分)
21.解:(1)D(3分)
∵父亲先从中随机抽取一张,小宁再从剩下的3张卡片中随机抽取一张,∴小宁和父亲抽到的球桌号不一样,它为必然事件.
(2)画树状图为:
共有12种等可能的结果,其中小宁和父亲最终观看“T4”球桌比赛的结果数为6,∴小宁和父亲最终观看“T4”球桌比赛的概率==.(8分)
22.解:(1)把点A(2,m)代入y=x+1,解得m=2,∴A(2,2),
把点A(2,2)代入y=,解得k=4,
∴反比例函数的解析式为y=;(4分)
(2)解方程组得或(舍),
∴点B的坐标为(-4,-1).(8分)
23.解:(1)证明:∵四边形ABCD是矩形,∴∠B=90°,AD∥BC,∴∠AEB=∠DAF,
∵DF⊥AE,∴∠DFA=90°,∴∠B=∠DFA,∴△ABE∽△DFA.(4分)
(2)∵△ABE∽△DFA,
∴=,
∵BC=4,E是BC的中点,∴BE=BC=×4=2,
∴在Rt△ABE中,AE===2,
∵AD=BC=4,∴=,
∴DF=.(10分)
24.解:(1)如图,过点A作AN⊥x轴于点N.
∵CD∶AD=1∶2,∴AC=3CD,OA=AD=2CD,
∵OA2+AC2=OC2,OC=,
∴(2CD)2+(3CD)2=()2,解得CD=,
∴OA=,AC=,∴AN·OC=OA·AC,∴AN=×.
∴AN=3,ON=2,∴点A的坐标为(2,3),
∴k=2×3=6.(5分)
(2)如图,过点B作BE⊥x轴于点E.
易证△AON≌△OBE,∴OE=AN=3,BE=ON=2,∴点B的坐标为(3,-2).
设直线AB的关系式为y=kx+b,
∵点A(2,3),B(3,-2)在直线AB上,
∴,∴,
∴直线AB的解析式为y=-5x+13.(10分)
25.解:(1)四边形AEA'D的形状是正方形.(2分)
(2)MC'=ME.(3分)
理由如下:如图,连接EC',由(1)知AD=AE,
∵四边形ABCD是矩形,∴AD=BC,∠EAC'=∠B=90°,
由折叠知B'C'=BC,∠B'=∠B,
∴AE=B'C',∠EAC'=∠B'=90°,
∵EC'=C'E,∴Rt△EC'A≌Rt△C'EB',
∴∠C'EA=∠EC'B',
∴MC'=ME.(7分)
(3)∵Rt△EC'A≌Rt△C'EB',
∴AC'=B'E,
由折叠知B'E=BE,∴AC'=BE,
∵AC'=2 cm,DC'=4 cm,∴AB=CD=2+4+2=8 cm.
设DF=x cm,则FC'=FC=(8-x) cm,
在Rt△DC'F中,由勾股定理得42+x2=(8-x)2,解得x=3,
即DF=3 cm.
如图,延长BA,FC'交于点G,
∵AG∥DF,∴△AC'G∽△DC'F,∴=,∴==,
∴AG= cm,∴EG=+6= cm,
∵DF∥EG,∴△DNF∽△ENG,
∴DN︰EN=DF︰EG=3︰=2︰5.(12分)
时间:90分钟 满分:120分 考试范围:上册全部
一、选择题(本题共10小题,每小题3分,共30分)
1.下列线段中,能成比例的是 ( )
A.3 cm,4 cm,5 cm,6 cm B.3 cm,5 cm,6 cm,9 cm
C.3 cm,6 cm,7 cm,10 cm D.3 cm,6 cm,7 cm,14 cm
2.如图,一个圆柱体被截去一部分,则该几何体的主视图是 ( )
3.若关于x的一元二次方程x2-mx+2=0的一个根是1,则m的值是 ( )
A.1 B.2 C.3 D.4
4.下列各点在反比例函数y=-的图象上的是 ( )
A.(-1,-2021) B.(1,2021)
C.(-1,) D.(,-)
5.如图,夜晚路灯下有一排同样高的旗杆,离路灯越近,旗杆的影子 ( )
A.越长 B.越短
C.一样长 D.随时间变化而变化
6.如图,在菱形ABOC中,AB=2,∠A=60°,菱形的一个顶点C在反比例函数y=(k≠0)的图象上,则反比例函数的解析式为 ( )
A.y=- B.y=-
C.y=- D.y=
7.从马航、张斌、王浩、李敏四人中抽调两人参加“寸草心”志愿服务队,恰好抽到马航和李敏的概率是 ( )
A. B. C. D.
8.已知x1,x2是方程x2-2x-7=0的两根,则-x1+x2的值为 ( )
A.9 B.7 C.5 D.3
9.如图,矩形ABCD的四个顶点分别在直线l3,l4,l2,l1上.若直线l1∥l2∥l3∥l4且间距相等,CB交直线l3于点G,AB=4,BC=3,则的值为 ( )
A. B. C. D.
10.如图,在矩形ABCD中,AC,BD相交于点O,过点B作BF⊥AC交CD于点F,交AC于点M,过点D作DE∥BF交AB于点E,交AC于点N,连接FN,EM.则下列结论:①DN=BM;②EM∥FN;③AE=FC;④当AO=AD时,四边形DEBF是菱形.其中,正确结论的个数是 ( )
A.1 B.2 C.3 D.4
二、填空题(本题共6小题,每小题3分,共18分)
11.同一时刻,小明在阳光下的影长为2米,与他邻近的旗杆的影长为6米,小明的身高为1.6米,则旗杆的高为 米.
12.菱形的一条对角线长为8,其边长是方程x2-9x+20=0的一个根,则该菱形的周长为 .
13.一个圆柱的三视图如图所示,若其俯视图为圆,则这个圆柱的体积为 .
14.如图,在正方形ABCD中,已知点E是AD的中点,点F是CD上一点,且DF=CD,连接EF,BE,若BE=4,则EF= .
15.如图,某人与一座建筑物DE的距离AF=120 m,他站在A处,将自己的食指竖直举在右眼前,闭上左眼,将食指前后移动,使食指恰好将该建筑物遮住,若此时眼睛到食指的距离AG约为40 cm,食指的长约8 cm,则该建筑物的高度约是 m.
16.如图,已知直线y=mx+4分别与y轴,x轴交于A,B两点,且△ABO的面积为16,反比例函数的图象恰好经过AB的中点,则反比例函数的表达式为 .
三、解答题(本大题共9小题,共72分)
17.(6分)解方程:x(x-2)=2-x.
18.(6分)如图,当太阳光与地面上的树影成45°角时,树影投射在墙上的影高CD等于2米,若树根到墙的距离BC等于8米,试求树高AB.
19.(6分)如图,在四边形ABCD中,AB∥CD,AB=AD,AC平分∠BAD.求证:四边形ABCD是菱形.
20.(6分)如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,CD⊥AB,垂足为D,E为BC的中点,AE与CD交于点F,求DF的长.
21.(8分)乒乓球是我国的国球,比赛采用单局11分制,是一种世界流行的球类体育项目,比赛分团体、单打、双打等数种.在某站公开赛中,某直播平台同时直播4场男单四分之一比赛,四场比赛的球桌号分别为“T1”“T2”“T3”“T4”(假设4场比赛同时开始),小宁和父亲准备一同观看其中的某一场比赛,但两人的意见不统一,于是采用抽签的方式决定,抽签规则如下:将正面分别写有数字“1”“2”“3”“4”的四张卡片(除数字不同外,其余均相同),数字“1”“2”“3”“4”分别对应球桌号“T1”“T2”“T3”“T4”,背面朝上洗匀,父亲先从中随机抽取一张,小宁再从剩下的3张卡片中随机抽取一张,比较两人所抽卡片上的数字,观看较大的数字对应球桌的比赛.
(1)下列事件中属于必然事件的是 .
A.抽到的是小宁最终想要看的一场比赛的球桌号
B.抽到的是父亲最终想要看的一场比赛的球桌号
C.小宁和父亲抽到同一个球桌号
D.小宁和父亲抽到的球桌号不一样
(2)用列表法或画树状图法求小宁和父亲最终观看“T4”球桌比赛的概率.
22.(8分)如图,一次函数y=x+1的图象与反比例函数y=的图象相交于A(2,m)和B两点.
(1)求反比例函数的解析式;
(2)求点B的坐标.
23.(10分)如图,在矩形ABCD中,E是BC的中点,DF⊥AE,垂足为F.
(1)求证:△ABE∽△DFA.
(2)若AB=6,BC=4,求DF的长.
24.(10分)如图,点A是反比例函数y=(k>0)的图象上的一点,连接OA,在OA的右下方构造正方形AOBD,连接AB,延长AD,与x轴交于点C,点C的坐标为(,0),且CD∶AD=1∶2.
(1)求k的值;
(2)求直线AB的解析式.
25.(12分)实践操作:第一步:如图1,将矩形纸片ABCD沿过点D的直线折叠,使点A落在CD上的点A'处,得到折痕DE,然后把纸片展平.
第二步:如图2,将图1中的矩形纸片ABCD沿过点E的直线折叠,点C恰好落在AD上的点C'处,点B落在点B'处,得到折痕EF,B'C'交AB于点M,C'F交DE于点N,再把纸片展平.
问题解决:
(1)如图1,填空:四边形AEA'D的形状是 .
(2)如图2,线段MC'与ME是否相等 若相等,请给出证明;若不相等,请说明理由.
(3)如图2,若AC'=2 cm,DC'=4 cm,求DN︰EN的值.
参考答案
一、选择题
1 2 3 4 5 6 7 8 9 10
D C C D B B C A A D
1.D 【解析】通过计算可知,只有3 cm,6 cm,7 cm,14 cm四条线段能成比例.
2.C 【解析】从正面看是一个右上角截去一角的矩形.
3.C 【解析】将x=1代入方程x2-mx+2=0中即可解得m=3.
4.D 【解析】将各个选项中的点的坐标分别代入关系式验证,即可知应选D.
5.B 【解析】由图易得AB
7.C 【解析】列表如下,观察表格可知,总共有12种等可能的结果,符合要求的有2种,
马航 张斌 王浩 李敏
马航 (马航,张斌) (马航,王浩) (马航,李敏)
张斌 (张斌,马航) (张斌,王浩) (张斌,李敏)
王浩 (王浩,马航) (王浩,张斌) (王浩,李敏)
李敏 (李敏,马航) (李敏,张斌) (李敏,王浩)
所以恰好抽到马航和李敏的概率P==.
8.A 【解析】根据题意得x1+x2=2,-2x1-7=0,∴-2x1=7.∴-x1+x2=-2x1+x1+x2=7+2=9.
9.A 【解析】如图,作CF⊥l4于点F,交l3于点E.由已知可得,GE∥BF,CE=EF,∵BC=3,∴GB=.∵四边形ABCD是矩形,AB=4,∴CD=AB=4,∴===.
10.D 【解析】∵四边形ABCD是矩形,∴AB=CD,AD=BC,AD∥BC,∴∠DAN=∠BCM.∵BF⊥AC,DE∥BF,∴DE⊥AC,即∠AND=∠CMB=90°,∴△ADN≌△CBM,∴DN=BM,∠ADN=∠CBM,则△ADE≌△CBF,∴AE=FC,DE=BF,∴NE=MF,∴四边形EMFN是平行四边形,∴EM∥FN,即①②③都是正确的.由AE=CF,AB=CD,∴BE=DF,∴四边形DEBF是平行四边形.∵四边形ABCD是矩形,∴AO=DO.∵当AO=AD时,AO=DO=AD,∴△ADO是等边三角形,∴∠ADN=∠BDE=30°,∴∠BDE=∠ABD=30°,∴DE=BE,∴四边形DEBF是菱形,则④也是正确的.
二、填空题
11 12 13 14 15 16
4.8 20 24π 2 24 y=
11.4.8 【解析】设旗杆的高为x米,则有=,解得x=4.8.
12.20 【解析】解方程得x=4或x=5,分两种情况:①当AB=AD=4时,4+4=8,不能构成三角形;②当AB=AD=5时,5+5>8,即可得出菱形ABCD的周长为5×4=20.
13.24π 【解析】π()2×6=24π.
14.2 【解析】∵四边形ABCD是正方形,∴AB=BC=CD=AD,∠A=∠D=90°,∵点E是AD的中点,∴AE=DE=AD,∵DF=CD,∴DF=AD=×2AE=AE,在△ABE和△DEF中,==2,∠A=∠D,∴△ABE∽△DEF,∴==2.EF==2.
15.24 【解析】∵40 cm=0.4 m,8 cm=0.08 m,BC∥DE,AG⊥BC,AF⊥DE,∴△ABC∽△ADE,∴BC∶DE=AG∶AF,∴0.08∶DE=0.4∶120,∴DE=24 m.
16.y= 【解析】由题意可得A(0,4),△ABO的面积为16,∴OB=8,即B(8,0),∴AB的中点坐标为(4,2),设反比例函数的表达式为y=,得k=4×2=8,∴反比例函数的表达式为y=.
三、解答题
17.解:移项得x(x-2)+(x-2)=0,
方程左边提公因式得(x-2)(x+1)=0,即x-2=0或x+1=0,
∴x1=2,x2=-1.(6分)
18.解:如图,过点D作DH⊥AB于点H,则DH=CB=8米.
在Rt△ADH中,∵∠ADH=45°,∴∠DAB=45°,∴AH=DH=8.
∴AB=AH+HB=8+2=10.
即树高AB等于10米.(6分)
19.证明:∵AB∥CD,∴∠BAC=∠DCA,
∵AC平分∠BAD,∴∠DAC=∠BAC,∴∠DAC=∠DCA,∴AD=CD,
∵AB=AD,∴AB=CD,
∵AB∥CD,∴四边形ABCD是平行四边形.
∵AB=AD,∴四边形ABCD是菱形.(6分)
20.解:∵∠ACB=90°,AC=3,BC=4,由勾股定理得AB=5,
∵CD⊥AB,∴AC·BC=AB·CD,∴CD=.
由勾股定理得AD=,BD=.(3分)
过点E作EG∥AB交CD于点G,DG=CD=,EG=BD=,
∵=,∴=,∴DF=.(6分)
21.解:(1)D(3分)
∵父亲先从中随机抽取一张,小宁再从剩下的3张卡片中随机抽取一张,∴小宁和父亲抽到的球桌号不一样,它为必然事件.
(2)画树状图为:
共有12种等可能的结果,其中小宁和父亲最终观看“T4”球桌比赛的结果数为6,∴小宁和父亲最终观看“T4”球桌比赛的概率==.(8分)
22.解:(1)把点A(2,m)代入y=x+1,解得m=2,∴A(2,2),
把点A(2,2)代入y=,解得k=4,
∴反比例函数的解析式为y=;(4分)
(2)解方程组得或(舍),
∴点B的坐标为(-4,-1).(8分)
23.解:(1)证明:∵四边形ABCD是矩形,∴∠B=90°,AD∥BC,∴∠AEB=∠DAF,
∵DF⊥AE,∴∠DFA=90°,∴∠B=∠DFA,∴△ABE∽△DFA.(4分)
(2)∵△ABE∽△DFA,
∴=,
∵BC=4,E是BC的中点,∴BE=BC=×4=2,
∴在Rt△ABE中,AE===2,
∵AD=BC=4,∴=,
∴DF=.(10分)
24.解:(1)如图,过点A作AN⊥x轴于点N.
∵CD∶AD=1∶2,∴AC=3CD,OA=AD=2CD,
∵OA2+AC2=OC2,OC=,
∴(2CD)2+(3CD)2=()2,解得CD=,
∴OA=,AC=,∴AN·OC=OA·AC,∴AN=×.
∴AN=3,ON=2,∴点A的坐标为(2,3),
∴k=2×3=6.(5分)
(2)如图,过点B作BE⊥x轴于点E.
易证△AON≌△OBE,∴OE=AN=3,BE=ON=2,∴点B的坐标为(3,-2).
设直线AB的关系式为y=kx+b,
∵点A(2,3),B(3,-2)在直线AB上,
∴,∴,
∴直线AB的解析式为y=-5x+13.(10分)
25.解:(1)四边形AEA'D的形状是正方形.(2分)
(2)MC'=ME.(3分)
理由如下:如图,连接EC',由(1)知AD=AE,
∵四边形ABCD是矩形,∴AD=BC,∠EAC'=∠B=90°,
由折叠知B'C'=BC,∠B'=∠B,
∴AE=B'C',∠EAC'=∠B'=90°,
∵EC'=C'E,∴Rt△EC'A≌Rt△C'EB',
∴∠C'EA=∠EC'B',
∴MC'=ME.(7分)
(3)∵Rt△EC'A≌Rt△C'EB',
∴AC'=B'E,
由折叠知B'E=BE,∴AC'=BE,
∵AC'=2 cm,DC'=4 cm,∴AB=CD=2+4+2=8 cm.
设DF=x cm,则FC'=FC=(8-x) cm,
在Rt△DC'F中,由勾股定理得42+x2=(8-x)2,解得x=3,
即DF=3 cm.
如图,延长BA,FC'交于点G,
∵AG∥DF,∴△AC'G∽△DC'F,∴=,∴==,
∴AG= cm,∴EG=+6= cm,
∵DF∥EG,∴△DNF∽△ENG,
∴DN︰EN=DF︰EG=3︰=2︰5.(12分)
同课章节目录
