北师大版六年级下册数学第一单元圆柱与圆锥应用题训练(含解析)
文档属性
| 名称 | 北师大版六年级下册数学第一单元圆柱与圆锥应用题训练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1002.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 07:53:46 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
北师大版六年级下册数学第一单元圆柱与圆锥应用题训练
1.一个圆锥形沙堆,量得底面周长是12.56米,高是1.5米,把这堆沙全部铺在一个圆柱形沙坑内,这个沙坑的底面半径是2米。这堆沙平均能铺多厚?
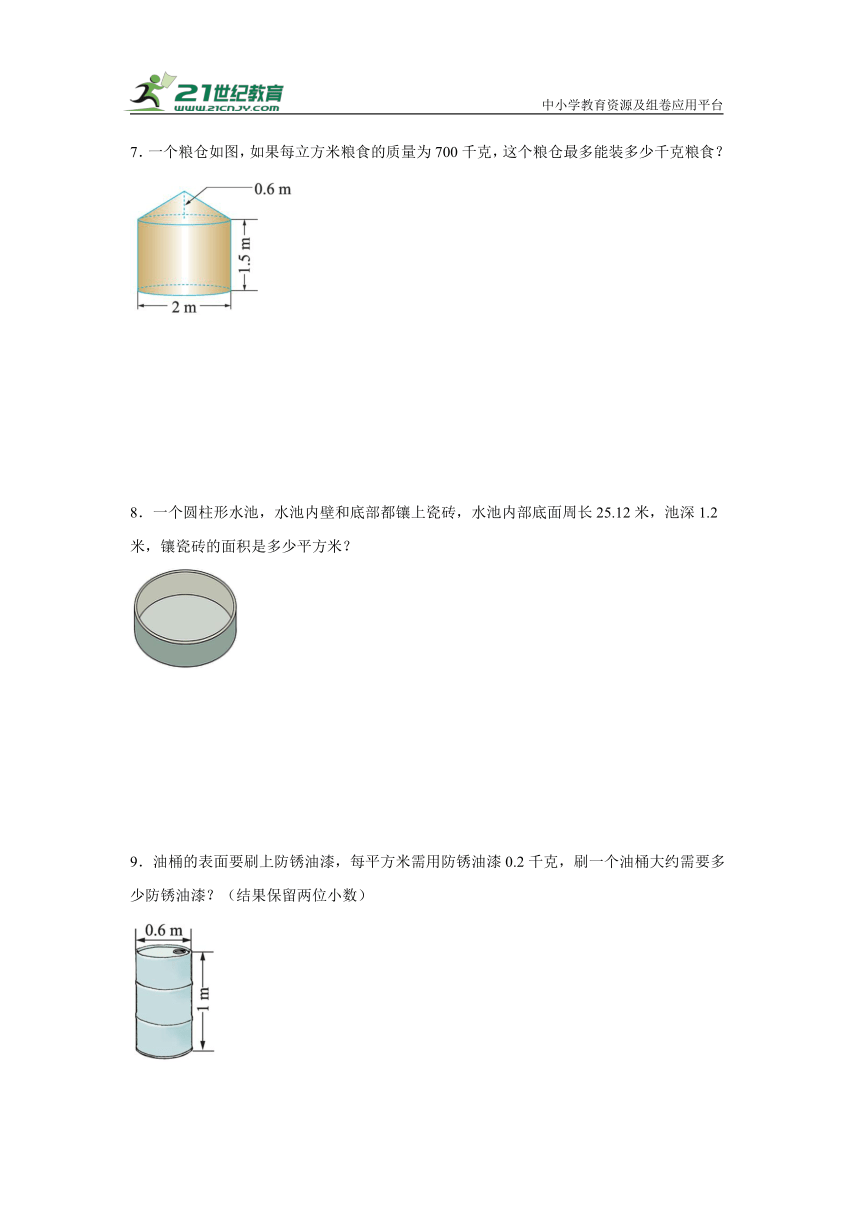
2.一个底面半径为10厘米的圆柱形容器,里面装有水。将等底等高的一个圆柱形铁块和一个圆锥形铁块同时放入这个容器中,水面上升到9厘米(如图)。这个圆锥形铁块的体积是多少?
3.如图,一个底面直径是20厘米的圆柱形容器,将一个底面半径是3厘米,高是10厘米的圆锥形铁块完全浸入水中。当把铁块取出时,这时水面的高度会下降多少厘米?
4.为了发展农村绿色能源,幸福村要挖一个圆柱形的沼气池,底面半径是4米、深2.5米。(π取值为3.14)
(1)这个沼气池的容积是多少立方米?
(2)如果要在沼气池的底部和四周铺上一种防漏水膜,大约需要铺多大面积的防漏水膜?
5.如图,先将甲容器注满水,再将水倒入乙容器,这时乙容器中的水有多高?
6.建筑工地上有一个圆锥形的沙土堆,底面面积是24平方米,高3米。把这些沙土平填在一个长6米,宽4米的长方体土坑中,沙土厚多少米?
7.一个粮仓如图,如果每立方米粮食的质量为700千克,这个粮仓最多能装多少千克粮食?
8.一个圆柱形水池,水池内壁和底部都镶上瓷砖,水池内部底面周长25.12米,池深1.2米,镶瓷砖的面积是多少平方米?
9.油桶的表面要刷上防锈油漆,每平方米需用防锈油漆0.2千克,刷一个油桶大约需要多少防锈油漆?(结果保留两位小数)
10.压路机前轮直径是1.6米,宽是2米,它转动一周,压路的面积是多少平方米?
11.一个圆柱形橡皮泥,底面积是12平方厘米,高是5厘米。
(1)如果把它捏成同样底面大小的圆锥,这个圆锥的高是多少?
(2)如果把它捏成同样高的圆锥,这个圆锥的底面积是多少?
12.如图,测量中经常使用铅锤。这个铅锤的体积是多少立方厘米?(结果保留两位小数)
13.一个长方体的木块,它的长、宽、高的比是。这个长方体木块的长是24厘米,现在将这个长方体木块削成一个体积最大的圆锥,这个圆锥的体积是多少立方厘米?
14.一个圆锥形的沙堆,底面积是1884平方米,高4米,把这堆沙铺在宽10米的公路路面上,如果铺0.02米厚,能铺多长?
15.下面是一个零件的示意图(单位:厘米),它是由一个长方体从前往后挖掉(挖通)一个底面直径为10厘米的圆柱体得到的,求这个零件的体积。(π取3.14)
16.陀螺是一种传统的儿童玩具,如今它已成为一种体育项目。如图形状的陀螺,上面呈圆柱形,下面呈圆锥形。圆柱的底面半径为4厘米,高5厘米;圆锥部分的高为6厘米。
(1)给陀螺的圆柱形部分涂上红色,圆锥形部分涂上黄色,那么涂红色部分的面积有多大?
(2)这个陀螺的体积是多少立方厘米?
17.一个圆柱沿直径切开表面积增加12平方厘米,如果切成三个小圆柱,表面积增加48平方厘米,则原来圆柱的体积是多少立方厘米?(π取3)
18.小明家把今年收获的小麦堆成了圆锥形,高3米,底面直径是4米。
(1)如果每立方米小麦重700千克,这堆小麦重多少千克?
(2)如果把这堆小麦倒入一个底面直径为2米的圆柱形铁桶中刚好装满,那么铁桶高多少米?
19.一种压路机的前轮是圆柱形的,轮宽1.6米,直径是0.8米。前轮滚动一周,压路的面积是多少平方米?(π取3)
20.妈妈的茶杯高15厘米(如图),茶杯中部那圈装饰带是今年“母亲节”淘气花10元钱为妈妈购买的礼物,这样妈妈再也不担心烫伤手了。已知这条装饰带宽5厘米,它的面积是多少?
21.把一个底面半径是6cm,高是8cm的铁制圆锥放入盛满水的桶里,将有多少立方厘米的水溢出?
22.一个蓄水桶,从里面量,底面半径是5分米,深是10分米。
(1)这个蓄水桶最多可以装水多少升?
(2)做一个这样的无盖蓄水桶,需要铁皮多少平方米?
23.一个底面半径是3厘米的圆锥,高为20厘米,将这个圆锥铁块熔铸成一个宽5厘米、高4厘米的长方体,长方体的长是多少厘米?
24.如图所示茶杯。
(1)茶杯中的一圈装饰,是为防烫手贴上的,这条装饰带宽5厘米,长至少是多少厘米?(接头忽略不计)
(2)这个茶杯的容积大约是多少毫升?
25.李叔叔把一车沙子卸到地面上形成一个圆锥形沙堆,这个沙堆的底面直径是2米,高1.5米,这堆沙子的占地面积是多少平方米?如果每立方米沙子120元,李叔叔买这堆沙子需要花多少元?
26.“博士帽”被视为博学的象征,如图所示的“博士帽”是用黑色卡纸做成的,上面是边长为30厘米的正方形,下面是底面直径为16厘米、高为10厘米的无底无盖圆柱。制作这样的一顶“博士帽”至少需要多少平方厘米的黑色卡纸?
27.2023年5月30日,我国长征二号F运载火箭搭载神舟十六号载人飞船顺利升空并取得园满成功。整流置是运载火箭的重要组成部分,外形通常由近似的圆柱和圆锥组成。学校创客小组制作了运载火箭整流置的模型(如图所示),请问这个整流置模型的体积是多少?
28.在一只底面半径是30厘米,高50厘米的圆柱形水桶里,装有水和一个半径为10厘米的圆锥形钢材(钢材完全浸没在水中),如果把钢材从水中完全取出后桶里的水面下降了1厘米,这个圆锥形钢材的高是多少厘米?
29.琳琳刚刚学习了圆柱的体积,就对家里的圆柱体卷纸做起了研究:她想知道卷纸拉开究竟有多长。于是用工具测是了一些数据,她在计算过程中,还发现有一个数据是可以不用测量的。
(1)不用测量的这个数据是( )。
(2)你来算算看,卷纸拉开后长度是多少米?
30.如图1,某种油菜籽榨油机的漏斗是由圆柱和圆锥两部分组成的。底面半径是4分米,这两部分的高都是6分米。每立方分米油菜籽重0.5千克。
图1 图2
(1)这个漏斗最多能装多少千克油菜籽?
(2)如果张师傅打算用铁皮给这个漏斗做一个圆柱形的防尘罩(如图2,没有下底面),至少需要多少平方分米铁皮?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
《北师大版六年级下册数学第一单元圆柱与圆锥应用题训练》参考答案
1.0.5米
【分析】由题意可知,圆锥的体积与圆柱的体积相等,根据圆的周长公式的逆运算,用周长除以圆周率再除以2可得半径,再根据圆锥的体积公式,代入数据可得圆锥体积,即圆柱体积,最后根据圆柱体积公式的逆运算,用体积除以圆周率再除以半径的平方,即可得解。
【详解】
(米)
答:这堆沙平均能铺0.5米厚。
2.314立方厘米
【分析】水面上升的体积,就是圆柱和圆锥铁块的体积。由题意可知,圆柱形容器水面升高了厘米,根据圆柱的体积计算公式,即可求出水面上升的体积,即圆柱和圆锥的体积和,等底等高的圆柱的体积是圆锥体积的3倍,利用体积除以(3+1)即可求出圆锥的体积。
【详解】3.14×102×(9-5)÷(3+1)
=3.14×100×4÷4
=314(立方厘米)
答:这个圆锥形铁块的体积是314立方厘米。
3.0.3厘米
【分析】根据体积的意义可知,当把圆锥形铁块从容器中取出后,下降部分水的体积就等于这个圆锥形铁块的体积。
先根据圆锥的体积公式:V=πr2h,把数据代入公式求出圆锥形铁块的体积;
根据圆的面积公式,求出圆柱的底面积;再根据圆柱的高,用下降部分水的体积除以除以圆柱形容器的底面积,即可求出水面下降的高度。
【详解】×3.14×32×10÷[3.14×(20÷2)2]
=×3.14×9×10÷[3.14×102]
=×3.14×9×10÷[3.14×100]
=94.2÷314
=0.3(厘米)
答:这时水面的高度会下降0.3厘米。
4.(1)125.6立方米
(2)113.04平方米
【分析】(1)根据圆柱的体积(容积):V=sh=πr2h,代入数据计算即可求出这个沼气池的容积。
(2)防漏水膜的面积=底面面积+侧面积,根据圆的面积:S=πr2,侧面积:S=ch=2πrh,代入数据计算即可。
【详解】(1)3.14×42×2.5
=3.14×16×2.5
=125.6(立方米)
答:这个沼气池的容积是125.6立方米。
(2)3.14×42+3.14×4×2×2.5
=3.14×16+3.14×4×2×2.5
=50.24+62.8
=113.04(平方米)
答:大约需要铺113.04平方米的防漏水膜。
5.6厘米
【分析】由图可知,甲乙两个容器等底等高,则甲容器的容积等于乙容器容积的;用18乘,即可求出乙容器中水的高度。
【详解】18×=6(厘米)
答:这时乙容器中的水有6厘米。
6.1米
【分析】已知圆锥形沙土堆的底面面积是24平方米,高3米,根据圆锥的体积公式V=Sh,代入数据计算,求出沙土的体积;
把这些沙土平填在一个长6米,宽4米的长方体土坑中,沙土的体积不变;根据长方体的体积=长×宽×高,可知长方体的高=体积÷长÷宽,代入数据计算,求出沙土的厚度。
【详解】×24×3=24(立方米)
24÷6÷4
=4÷4
=1(米)
答:沙土厚1米。
7.3736.6千克
【分析】从图中可知,粮仓的上面是圆锥、下面是圆柱;根据圆柱的体积(容积)公式V=πr2h,圆锥的体积(容积)公式V=πr2h,代入数据计算,求出圆柱、圆锥的容积,再相加,即是这个粮仓的容积;然后用每立方米粮食的质量乘粮仓的容积,即可求出这个粮仓最多能装粮食的质量。
【详解】2÷2=1(米)
3.14×12×1.5+×3.14×12×0.6
=3.14×1×1.5+×3.14×1×0.6
=4.71+0.628
=5.338(立方米)
700×5.338=3736.6(千克)
答:这个粮仓最多能装3736.6千克粮食。
8.80.384平方米
【分析】已知圆柱形水池的底面周长25.12米,根据圆的周长公式C=2πr,可知r=C÷π÷2,由此求出圆柱的底面半径;
在水池内壁和底部都镶上瓷砖,镶瓷砖的面是圆柱的侧面和底面;根据S侧=Ch,S底=πr2,代入数据计算,求出圆柱的侧面积与底面积,再相加,即是镶瓷砖的面积。
【详解】25.12÷3.14÷2
=8÷2
=4(米)
25.12×1.2+3.14×42
=30.144+3.14×16
=30.144+50.24
=80.384(平方米)
答:镶瓷砖的面积是80.384平方米。
9.0.49千克
【分析】观察可知,已知圆柱油桶的底面直径是0.6米,高是1米,要求油桶表面刷的油漆,得先求圆柱的表面积,根据、、底面积公式,半径=直径÷2,代入数据计算圆柱的表面积,再乘0.2即可得解,结果采用“四舍五入法”保留两位小数。
【详解】
(千克)
答:刷一个油桶大约需要0.49千克防锈油漆。
10.10.048平方米
【分析】由题意可知,求压路面积就是求压路机前轮的侧面积,根据圆柱的侧面积公式,已知圆柱的底面直径是1.6米,高是2米,代入数据计算即可。
【详解】
(平方米)
答:压路面积是10.048平方米。
11.(1)15厘米;
(2)36平方厘米
【分析】由题意可知,把圆柱形橡皮泥捏成圆锥形橡皮泥后,虽然橡皮泥的形状发生变化,但是橡皮泥的体积不变。当圆柱和圆锥的体积和底面积相等时,圆锥的高是圆柱高的3倍,圆柱的高是圆锥高的;当圆柱和圆锥的体积和高相等时,圆锥的高是圆柱高的3倍,圆柱的高是圆锥高的,据此解答。
【详解】(1)5×3=15(厘米)
答:这个圆锥的高是15厘米。
(2)12×3=36(平方厘米)
答:这个圆锥的底面积是36平方厘米。
12.16.75立方厘米
【分析】由图可知,铅锤的底面半径是4÷2=2(厘米),铅锤的高是4厘米,利用“”求出铅锤的体积,注意结果保留两位小数;据此解答。
【详解】
=
=
=
≈16.75(立方厘米)
答:这个铅锤的体积是16.75立方厘米。
13.1017.36立方厘米
【分析】长方体的12条棱分为三组,互相平行的一组是4条,根据题意,可知长占长+宽+高的和的,已知一个数的几分之几是多少,求这个数,用除法,先求出长+宽+高的和,再用乘法分别求出它的宽、高,再确定“将这个长方体削成一个体积最大的圆锥”,这个圆锥体的底面直径应该是长方体的宽,圆锥体的高等于长方体的高,根据圆锥的体积计算公式解答。
【详解】
(厘米)
(厘米)
(厘米)
体积:
(立方厘米)
答:这个圆锥的体积是1017.36立方厘米。
14.12560米
【分析】已知圆锥形沙堆的底面积是1884平方米,高4米,根据圆锥的体积公式VSh,求出沙堆的体积;
再把这堆沙铺在宽10米、厚0.02米的公路路面上,根据长方体的体积公式V=abh,可知长方体的长a=V÷b÷h,据此求出能铺的长度。
【详解】1884×4
=628×4
=2512(立方米)
2512÷10÷0.02
=251.2÷0.02
=12560(米)
答:能铺12560米。
15.2607.5立方厘米
【分析】通过观察图形可知,这个零件的体积等于长方体的体积减去圆柱的体积,根据长方体的体积公式:V=abh,圆柱的体积公式:V=πr2h,半径r=d2,把数据代入公式解答。
【详解】30×5×20-3.14×(10÷2)2×5
=
=150×20-3.14×25×5
=3000-392.5
=2607.5(立方厘米)
答:这个零件的体积是2607.5立方厘米。
16.(1)175.84平方厘米;(2)351.68立方厘米
【分析】(1)圆柱部分涂红色部分的面积等于圆柱的一个底面积加上圆柱的侧面积,圆柱的底面积=×半径的平方,圆柱的侧面积=2rh,据此代入数据解答。
(2)陀螺的体积等于底面半径为4厘米,高5厘米的圆柱的体积与底面半径为4厘米,高6厘米的圆锥的体积,根据圆柱的体积=h,圆锥的体积=h解答。
【详解】(1)3.14×+2×3.14×4×5
=3.14×16+6.28×4×5
=50.24+25.12×5
=50.24+125.6
=175.84(平方厘米)
答:涂红色部分的面积是175.84平方厘米。
(2)3.14××5+×3.14××6
=3.14×16×5+2×3.14×16
=3.14×80+6.28×16
=251.2+100.48
=351.68(立方厘米)
答:这个陀螺的体积是351.68立方厘米。
17.18立方厘米
【分析】切成三个小圆柱,则增加了4个底面积,用求出底面积,再根据圆的面积公式的逆运算,求出半径,再用半径乘2得到直径;圆柱沿直径切开表面积增加12平方厘米,即增加了2个底面直径乘高的面积,用12除以2,再除以直径得到高;最后根据,代入数据计算即可得解。
【详解】48÷4÷3=4(平方厘米)
因为2×2=4,所以这个圆柱的底面半径是2厘米。
所以圆柱的高是:12÷2÷(2×2)
=12÷2÷4
=6÷4
=1.5(厘米)
则圆柱的体积是:48÷4×1.5
=12×1.5
=18(立方厘米)
答:原来圆柱的体积是18立方厘米。
18.(1)8792千克
(2)4米
【分析】(1)根据圆锥体积=底面积×高÷3,求出小麦体积,小麦体积×每立方米质量=这堆小麦的质量;
(2)根据圆柱的高=体积÷底面积,列式解答即可。
【详解】(1)3.14×(4÷2)2×3÷3
=3.14×22×3÷3
=3.14×4×3÷3
=12.56(立方米)
12.56×700=8792(千克)
答:这堆小麦重8792千克。
(2)12.56÷[3.14×(2÷2)2]
=12.56÷[3.14×12]
=12.56÷[3.14×1]
=12.56÷3.14
=4(米)
答:铁桶高4米。
19.3.84平方米
【分析】分析题目,求压路的面积就是求圆柱的侧面积,圆柱的侧面积公式:S=πdh,据此代入数据计算即可。
【详解】3×0.8×1.6
=2.4×1.6
=3.84(平方米)
答:前轮滚动一周,压路的面积是3.84平方米。
20.94.2平方厘米
【分析】观察可知,沉着茶杯的高把装饰带剪开,会得到一个长方形,长方形的长等于茶杯的底面周长,宽是5厘米,根据圆的周长公式,长方形的面积=长宽,代入数据计算即可得解。
【详解】
(平方厘米)
答:它的面积是94.2平方厘米。
21.301.44立方厘米
【分析】求溢出的水的体积,就是求圆锥的体积,根据圆锥的体积公式,代入数据计算即可。
【详解】
(立方厘米)
答:将有301.44立方厘米的水溢出。
22.(1)785升
(2)392.5平方分米
【分析】(1)根据圆柱的容积公式:容积=底面积×高,代入数据,求出蓄水桶的容积,注意单位名数的换算;
(2)求需要铁皮的面积,就是求这个圆柱形蓄水桶的表面积,因为是无盖,需要铁皮的面积=圆柱的表面积=底面积+侧面积;代入数据,即可解答。
【详解】(1)3.14×52×10
=3.14×25×10
=78.5×10
=785(立方分米)
785立方分米=785升
答:这个蓄水桶最多可以装水785升。
(2)3.14×52+3.14×5×2×10
=3.14×25+15.7×2×10
=78.5+31.4×10
=78.5+314
=392.5(平方分米)
答:做一个这样无盖蓄水桶,需要铁皮392.5平方分米。
23.9.42厘米
【分析】根据圆锥的体积公式:体积=底面积×高×,代入数据,求出圆锥的体积,圆锥铁块熔铸成长方体,体积不变,用圆锥的体积除以长方体的宽,再除以长方体的高,即可求出长方体的长。
【详解】3.14×32×20×÷5÷4
=3.14×9×20×÷5÷4
=28.26×20×÷5÷4
=565.2×÷5÷4
=188.4÷5÷4
=37.68÷4
=9.42(厘米)
答:长方体的长是9.42厘米。
24.(1)31.4厘米(2)1177.5毫升
【分析】(1)装饰带的长就是圆柱的底面周长,根据圆的周长C=πd,代入数据计算,即可求出这条装饰带长至少是多少厘米。
(2)根据圆柱的体积=底面积×高,代入数据计算,即可求出这个茶杯的容积。据此解答。
【详解】(1)10×3.14=31.4(厘米)
答:长至少是31.4厘米。
(2)10÷2=5(厘米)
3.14×52×15
=3.14×25×15
=1177.5(立方厘米)
1177.5立方厘米=1177.5毫升
答:这个茶杯的容积大约是1177.5毫升。
25.3.14平方米;188.4元
【分析】这堆沙子的占地面积,就是圆锥形沙堆的底面积,根据圆的面积公式:S=,代入数据解答即可;根据圆锥的体积=底面积×高÷3,求出圆锥形沙堆的体积,再用体积乘每立方米沙子的钱数即可解答。
【详解】2÷2=1(米)
3.14×=3.14(平方米)
3.14×1.5÷3×120
=4.71÷3×120
=1.57×120
=188.4(元)
答:这堆沙子的占地面积是3.14平方米,李叔叔买这堆沙子需要花188.4元。
26.1402.4平方厘米
【分析】根据题意,这种“博士帽”的上面是正方形,下面是无盖无底的圆柱,所以制作一顶“博士帽”至少需要卡纸的面积=正方形的面积+圆柱的侧面积;根据正方形的面积公式S=a2,圆柱的侧面积公式S=πdh,代入数据计算,求出制作一顶“博士帽”至少需要卡纸的面积。
【详解】3.14×16×10+30×30
=50.24×10+900
=502.4+900
=1402.4(平方厘米)
答:制作这样的一顶“博士帽”至少需要1402.4平方厘米的黑色卡纸。
27.18.84立方分米
【分析】这个整流置模型的体积等于底面直径是2分米,高是5分米的圆柱的体积加上底面直径是2分米,高是(8-5)分米的圆锥的体积,根据圆柱的体积公式:体积=底面积×高,圆锥的体积公式:体积=底面积×高×,代入数据,即可解答。
【详解】3.14×(2÷2)2×5+3.14×(2÷2)2×(8-5)×
=3.14×12×5+3.14×12×3×
=3.14×1×5+3.14×1×3×
=3.14×5+3.14×3×
=15.7+9.42×
=15.7+3.14
=18.84(立方分米)
答:这个整流置模型的体积是18.84立方分米。
28.27厘米
【分析】根据题意,把圆锥形钢材从水中完全取出后桶里的水面下降了1厘米,那么水下降的体积等于这个圆锥形钢材的体积;水下降部分是一个底面半径为30厘米、高1厘米的圆柱体,根据圆柱的体积公式V=πr2h,求出水下降部分的体积,也就是圆锥的体积;
已知圆锥形钢材的底面半径为10厘米,根据圆的面积公式S=πr2,求出钢材的底面积;再根据圆锥的高h=3V÷S,求出这个圆锥形钢材的高。
【详解】水下降部分的体积(圆锥的体积):
3.14×302×1
=3.14×900×1
=2826(立方厘米)
圆锥的底面积:
3.14×102
=3.14×100
=314(平方厘米)
圆锥的高:
2826×3÷314
=8478÷314
=27(厘米)
答:这个圆锥形钢材的高是27厘米。
29.(1)卷纸的高
(2)14.13米
【分析】(1)计算卷纸拉开究竟有多长,不需要知道卷纸的高,即不用测量的数据是卷纸的高。
(2)卷纸拉开底面由圆转化成长方形,长方形的面积=底面积,长方形的宽=卷纸的厚度,长方形的长就是卷纸拉开后的长度,根据圆的面积=圆周率×半径的平方,求出底面积,即长方形面积,根据长方形的长=面积÷宽,即可求出卷纸拉开后的长度。
【详解】(1)不用测量的这个数据是卷纸的高。
(2)6÷2=3(厘米)
(厘米)
答:卷纸拉开后长度是14.13米。
30.(1)200.96千克
(2)455.3平方分米
【分析】(1)漏斗的容积=圆柱的容积+圆锥的容积,圆柱的容积=底面积×高,圆锥的容积=底面积×高÷3,据此求出漏斗的容积,漏斗的容积×每立方分米油菜籽的质量=漏斗最多装的油菜籽质量。
(2)防尘罩没有下底面,防尘罩的表面积=底面积+侧面积,侧面积=底面周长×高,据此列式解答。
【详解】(1)3.14×42×6+3.14×42×6÷3
=3.14×16×6+3.14×16×6÷3
=301.44+100.48
=401.92(立方分米)
401.92×0.5=200.96(千克)
答:这个漏斗最多能装200.96千克油菜籽。
(2)3.14×(10÷2)2+3.14×10×12
=3.14×52+376.8
=3.14×25+376.8
=78.5+376.8
=455.3(平方分米)
答:至少需要455.3平方分米铁皮。
中小学教育资源及组卷应用平台
北师大版六年级下册数学第一单元圆柱与圆锥应用题训练
1.一个圆锥形沙堆,量得底面周长是12.56米,高是1.5米,把这堆沙全部铺在一个圆柱形沙坑内,这个沙坑的底面半径是2米。这堆沙平均能铺多厚?
2.一个底面半径为10厘米的圆柱形容器,里面装有水。将等底等高的一个圆柱形铁块和一个圆锥形铁块同时放入这个容器中,水面上升到9厘米(如图)。这个圆锥形铁块的体积是多少?
3.如图,一个底面直径是20厘米的圆柱形容器,将一个底面半径是3厘米,高是10厘米的圆锥形铁块完全浸入水中。当把铁块取出时,这时水面的高度会下降多少厘米?
4.为了发展农村绿色能源,幸福村要挖一个圆柱形的沼气池,底面半径是4米、深2.5米。(π取值为3.14)
(1)这个沼气池的容积是多少立方米?
(2)如果要在沼气池的底部和四周铺上一种防漏水膜,大约需要铺多大面积的防漏水膜?
5.如图,先将甲容器注满水,再将水倒入乙容器,这时乙容器中的水有多高?
6.建筑工地上有一个圆锥形的沙土堆,底面面积是24平方米,高3米。把这些沙土平填在一个长6米,宽4米的长方体土坑中,沙土厚多少米?
7.一个粮仓如图,如果每立方米粮食的质量为700千克,这个粮仓最多能装多少千克粮食?
8.一个圆柱形水池,水池内壁和底部都镶上瓷砖,水池内部底面周长25.12米,池深1.2米,镶瓷砖的面积是多少平方米?
9.油桶的表面要刷上防锈油漆,每平方米需用防锈油漆0.2千克,刷一个油桶大约需要多少防锈油漆?(结果保留两位小数)
10.压路机前轮直径是1.6米,宽是2米,它转动一周,压路的面积是多少平方米?
11.一个圆柱形橡皮泥,底面积是12平方厘米,高是5厘米。
(1)如果把它捏成同样底面大小的圆锥,这个圆锥的高是多少?
(2)如果把它捏成同样高的圆锥,这个圆锥的底面积是多少?
12.如图,测量中经常使用铅锤。这个铅锤的体积是多少立方厘米?(结果保留两位小数)
13.一个长方体的木块,它的长、宽、高的比是。这个长方体木块的长是24厘米,现在将这个长方体木块削成一个体积最大的圆锥,这个圆锥的体积是多少立方厘米?
14.一个圆锥形的沙堆,底面积是1884平方米,高4米,把这堆沙铺在宽10米的公路路面上,如果铺0.02米厚,能铺多长?
15.下面是一个零件的示意图(单位:厘米),它是由一个长方体从前往后挖掉(挖通)一个底面直径为10厘米的圆柱体得到的,求这个零件的体积。(π取3.14)
16.陀螺是一种传统的儿童玩具,如今它已成为一种体育项目。如图形状的陀螺,上面呈圆柱形,下面呈圆锥形。圆柱的底面半径为4厘米,高5厘米;圆锥部分的高为6厘米。
(1)给陀螺的圆柱形部分涂上红色,圆锥形部分涂上黄色,那么涂红色部分的面积有多大?
(2)这个陀螺的体积是多少立方厘米?
17.一个圆柱沿直径切开表面积增加12平方厘米,如果切成三个小圆柱,表面积增加48平方厘米,则原来圆柱的体积是多少立方厘米?(π取3)
18.小明家把今年收获的小麦堆成了圆锥形,高3米,底面直径是4米。
(1)如果每立方米小麦重700千克,这堆小麦重多少千克?
(2)如果把这堆小麦倒入一个底面直径为2米的圆柱形铁桶中刚好装满,那么铁桶高多少米?
19.一种压路机的前轮是圆柱形的,轮宽1.6米,直径是0.8米。前轮滚动一周,压路的面积是多少平方米?(π取3)
20.妈妈的茶杯高15厘米(如图),茶杯中部那圈装饰带是今年“母亲节”淘气花10元钱为妈妈购买的礼物,这样妈妈再也不担心烫伤手了。已知这条装饰带宽5厘米,它的面积是多少?
21.把一个底面半径是6cm,高是8cm的铁制圆锥放入盛满水的桶里,将有多少立方厘米的水溢出?
22.一个蓄水桶,从里面量,底面半径是5分米,深是10分米。
(1)这个蓄水桶最多可以装水多少升?
(2)做一个这样的无盖蓄水桶,需要铁皮多少平方米?
23.一个底面半径是3厘米的圆锥,高为20厘米,将这个圆锥铁块熔铸成一个宽5厘米、高4厘米的长方体,长方体的长是多少厘米?
24.如图所示茶杯。
(1)茶杯中的一圈装饰,是为防烫手贴上的,这条装饰带宽5厘米,长至少是多少厘米?(接头忽略不计)
(2)这个茶杯的容积大约是多少毫升?
25.李叔叔把一车沙子卸到地面上形成一个圆锥形沙堆,这个沙堆的底面直径是2米,高1.5米,这堆沙子的占地面积是多少平方米?如果每立方米沙子120元,李叔叔买这堆沙子需要花多少元?
26.“博士帽”被视为博学的象征,如图所示的“博士帽”是用黑色卡纸做成的,上面是边长为30厘米的正方形,下面是底面直径为16厘米、高为10厘米的无底无盖圆柱。制作这样的一顶“博士帽”至少需要多少平方厘米的黑色卡纸?
27.2023年5月30日,我国长征二号F运载火箭搭载神舟十六号载人飞船顺利升空并取得园满成功。整流置是运载火箭的重要组成部分,外形通常由近似的圆柱和圆锥组成。学校创客小组制作了运载火箭整流置的模型(如图所示),请问这个整流置模型的体积是多少?
28.在一只底面半径是30厘米,高50厘米的圆柱形水桶里,装有水和一个半径为10厘米的圆锥形钢材(钢材完全浸没在水中),如果把钢材从水中完全取出后桶里的水面下降了1厘米,这个圆锥形钢材的高是多少厘米?
29.琳琳刚刚学习了圆柱的体积,就对家里的圆柱体卷纸做起了研究:她想知道卷纸拉开究竟有多长。于是用工具测是了一些数据,她在计算过程中,还发现有一个数据是可以不用测量的。
(1)不用测量的这个数据是( )。
(2)你来算算看,卷纸拉开后长度是多少米?
30.如图1,某种油菜籽榨油机的漏斗是由圆柱和圆锥两部分组成的。底面半径是4分米,这两部分的高都是6分米。每立方分米油菜籽重0.5千克。
图1 图2
(1)这个漏斗最多能装多少千克油菜籽?
(2)如果张师傅打算用铁皮给这个漏斗做一个圆柱形的防尘罩(如图2,没有下底面),至少需要多少平方分米铁皮?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
《北师大版六年级下册数学第一单元圆柱与圆锥应用题训练》参考答案
1.0.5米
【分析】由题意可知,圆锥的体积与圆柱的体积相等,根据圆的周长公式的逆运算,用周长除以圆周率再除以2可得半径,再根据圆锥的体积公式,代入数据可得圆锥体积,即圆柱体积,最后根据圆柱体积公式的逆运算,用体积除以圆周率再除以半径的平方,即可得解。
【详解】
(米)
答:这堆沙平均能铺0.5米厚。
2.314立方厘米
【分析】水面上升的体积,就是圆柱和圆锥铁块的体积。由题意可知,圆柱形容器水面升高了厘米,根据圆柱的体积计算公式,即可求出水面上升的体积,即圆柱和圆锥的体积和,等底等高的圆柱的体积是圆锥体积的3倍,利用体积除以(3+1)即可求出圆锥的体积。
【详解】3.14×102×(9-5)÷(3+1)
=3.14×100×4÷4
=314(立方厘米)
答:这个圆锥形铁块的体积是314立方厘米。
3.0.3厘米
【分析】根据体积的意义可知,当把圆锥形铁块从容器中取出后,下降部分水的体积就等于这个圆锥形铁块的体积。
先根据圆锥的体积公式:V=πr2h,把数据代入公式求出圆锥形铁块的体积;
根据圆的面积公式,求出圆柱的底面积;再根据圆柱的高,用下降部分水的体积除以除以圆柱形容器的底面积,即可求出水面下降的高度。
【详解】×3.14×32×10÷[3.14×(20÷2)2]
=×3.14×9×10÷[3.14×102]
=×3.14×9×10÷[3.14×100]
=94.2÷314
=0.3(厘米)
答:这时水面的高度会下降0.3厘米。
4.(1)125.6立方米
(2)113.04平方米
【分析】(1)根据圆柱的体积(容积):V=sh=πr2h,代入数据计算即可求出这个沼气池的容积。
(2)防漏水膜的面积=底面面积+侧面积,根据圆的面积:S=πr2,侧面积:S=ch=2πrh,代入数据计算即可。
【详解】(1)3.14×42×2.5
=3.14×16×2.5
=125.6(立方米)
答:这个沼气池的容积是125.6立方米。
(2)3.14×42+3.14×4×2×2.5
=3.14×16+3.14×4×2×2.5
=50.24+62.8
=113.04(平方米)
答:大约需要铺113.04平方米的防漏水膜。
5.6厘米
【分析】由图可知,甲乙两个容器等底等高,则甲容器的容积等于乙容器容积的;用18乘,即可求出乙容器中水的高度。
【详解】18×=6(厘米)
答:这时乙容器中的水有6厘米。
6.1米
【分析】已知圆锥形沙土堆的底面面积是24平方米,高3米,根据圆锥的体积公式V=Sh,代入数据计算,求出沙土的体积;
把这些沙土平填在一个长6米,宽4米的长方体土坑中,沙土的体积不变;根据长方体的体积=长×宽×高,可知长方体的高=体积÷长÷宽,代入数据计算,求出沙土的厚度。
【详解】×24×3=24(立方米)
24÷6÷4
=4÷4
=1(米)
答:沙土厚1米。
7.3736.6千克
【分析】从图中可知,粮仓的上面是圆锥、下面是圆柱;根据圆柱的体积(容积)公式V=πr2h,圆锥的体积(容积)公式V=πr2h,代入数据计算,求出圆柱、圆锥的容积,再相加,即是这个粮仓的容积;然后用每立方米粮食的质量乘粮仓的容积,即可求出这个粮仓最多能装粮食的质量。
【详解】2÷2=1(米)
3.14×12×1.5+×3.14×12×0.6
=3.14×1×1.5+×3.14×1×0.6
=4.71+0.628
=5.338(立方米)
700×5.338=3736.6(千克)
答:这个粮仓最多能装3736.6千克粮食。
8.80.384平方米
【分析】已知圆柱形水池的底面周长25.12米,根据圆的周长公式C=2πr,可知r=C÷π÷2,由此求出圆柱的底面半径;
在水池内壁和底部都镶上瓷砖,镶瓷砖的面是圆柱的侧面和底面;根据S侧=Ch,S底=πr2,代入数据计算,求出圆柱的侧面积与底面积,再相加,即是镶瓷砖的面积。
【详解】25.12÷3.14÷2
=8÷2
=4(米)
25.12×1.2+3.14×42
=30.144+3.14×16
=30.144+50.24
=80.384(平方米)
答:镶瓷砖的面积是80.384平方米。
9.0.49千克
【分析】观察可知,已知圆柱油桶的底面直径是0.6米,高是1米,要求油桶表面刷的油漆,得先求圆柱的表面积,根据、、底面积公式,半径=直径÷2,代入数据计算圆柱的表面积,再乘0.2即可得解,结果采用“四舍五入法”保留两位小数。
【详解】
(千克)
答:刷一个油桶大约需要0.49千克防锈油漆。
10.10.048平方米
【分析】由题意可知,求压路面积就是求压路机前轮的侧面积,根据圆柱的侧面积公式,已知圆柱的底面直径是1.6米,高是2米,代入数据计算即可。
【详解】
(平方米)
答:压路面积是10.048平方米。
11.(1)15厘米;
(2)36平方厘米
【分析】由题意可知,把圆柱形橡皮泥捏成圆锥形橡皮泥后,虽然橡皮泥的形状发生变化,但是橡皮泥的体积不变。当圆柱和圆锥的体积和底面积相等时,圆锥的高是圆柱高的3倍,圆柱的高是圆锥高的;当圆柱和圆锥的体积和高相等时,圆锥的高是圆柱高的3倍,圆柱的高是圆锥高的,据此解答。
【详解】(1)5×3=15(厘米)
答:这个圆锥的高是15厘米。
(2)12×3=36(平方厘米)
答:这个圆锥的底面积是36平方厘米。
12.16.75立方厘米
【分析】由图可知,铅锤的底面半径是4÷2=2(厘米),铅锤的高是4厘米,利用“”求出铅锤的体积,注意结果保留两位小数;据此解答。
【详解】
=
=
=
≈16.75(立方厘米)
答:这个铅锤的体积是16.75立方厘米。
13.1017.36立方厘米
【分析】长方体的12条棱分为三组,互相平行的一组是4条,根据题意,可知长占长+宽+高的和的,已知一个数的几分之几是多少,求这个数,用除法,先求出长+宽+高的和,再用乘法分别求出它的宽、高,再确定“将这个长方体削成一个体积最大的圆锥”,这个圆锥体的底面直径应该是长方体的宽,圆锥体的高等于长方体的高,根据圆锥的体积计算公式解答。
【详解】
(厘米)
(厘米)
(厘米)
体积:
(立方厘米)
答:这个圆锥的体积是1017.36立方厘米。
14.12560米
【分析】已知圆锥形沙堆的底面积是1884平方米,高4米,根据圆锥的体积公式VSh,求出沙堆的体积;
再把这堆沙铺在宽10米、厚0.02米的公路路面上,根据长方体的体积公式V=abh,可知长方体的长a=V÷b÷h,据此求出能铺的长度。
【详解】1884×4
=628×4
=2512(立方米)
2512÷10÷0.02
=251.2÷0.02
=12560(米)
答:能铺12560米。
15.2607.5立方厘米
【分析】通过观察图形可知,这个零件的体积等于长方体的体积减去圆柱的体积,根据长方体的体积公式:V=abh,圆柱的体积公式:V=πr2h,半径r=d2,把数据代入公式解答。
【详解】30×5×20-3.14×(10÷2)2×5
=
=150×20-3.14×25×5
=3000-392.5
=2607.5(立方厘米)
答:这个零件的体积是2607.5立方厘米。
16.(1)175.84平方厘米;(2)351.68立方厘米
【分析】(1)圆柱部分涂红色部分的面积等于圆柱的一个底面积加上圆柱的侧面积,圆柱的底面积=×半径的平方,圆柱的侧面积=2rh,据此代入数据解答。
(2)陀螺的体积等于底面半径为4厘米,高5厘米的圆柱的体积与底面半径为4厘米,高6厘米的圆锥的体积,根据圆柱的体积=h,圆锥的体积=h解答。
【详解】(1)3.14×+2×3.14×4×5
=3.14×16+6.28×4×5
=50.24+25.12×5
=50.24+125.6
=175.84(平方厘米)
答:涂红色部分的面积是175.84平方厘米。
(2)3.14××5+×3.14××6
=3.14×16×5+2×3.14×16
=3.14×80+6.28×16
=251.2+100.48
=351.68(立方厘米)
答:这个陀螺的体积是351.68立方厘米。
17.18立方厘米
【分析】切成三个小圆柱,则增加了4个底面积,用求出底面积,再根据圆的面积公式的逆运算,求出半径,再用半径乘2得到直径;圆柱沿直径切开表面积增加12平方厘米,即增加了2个底面直径乘高的面积,用12除以2,再除以直径得到高;最后根据,代入数据计算即可得解。
【详解】48÷4÷3=4(平方厘米)
因为2×2=4,所以这个圆柱的底面半径是2厘米。
所以圆柱的高是:12÷2÷(2×2)
=12÷2÷4
=6÷4
=1.5(厘米)
则圆柱的体积是:48÷4×1.5
=12×1.5
=18(立方厘米)
答:原来圆柱的体积是18立方厘米。
18.(1)8792千克
(2)4米
【分析】(1)根据圆锥体积=底面积×高÷3,求出小麦体积,小麦体积×每立方米质量=这堆小麦的质量;
(2)根据圆柱的高=体积÷底面积,列式解答即可。
【详解】(1)3.14×(4÷2)2×3÷3
=3.14×22×3÷3
=3.14×4×3÷3
=12.56(立方米)
12.56×700=8792(千克)
答:这堆小麦重8792千克。
(2)12.56÷[3.14×(2÷2)2]
=12.56÷[3.14×12]
=12.56÷[3.14×1]
=12.56÷3.14
=4(米)
答:铁桶高4米。
19.3.84平方米
【分析】分析题目,求压路的面积就是求圆柱的侧面积,圆柱的侧面积公式:S=πdh,据此代入数据计算即可。
【详解】3×0.8×1.6
=2.4×1.6
=3.84(平方米)
答:前轮滚动一周,压路的面积是3.84平方米。
20.94.2平方厘米
【分析】观察可知,沉着茶杯的高把装饰带剪开,会得到一个长方形,长方形的长等于茶杯的底面周长,宽是5厘米,根据圆的周长公式,长方形的面积=长宽,代入数据计算即可得解。
【详解】
(平方厘米)
答:它的面积是94.2平方厘米。
21.301.44立方厘米
【分析】求溢出的水的体积,就是求圆锥的体积,根据圆锥的体积公式,代入数据计算即可。
【详解】
(立方厘米)
答:将有301.44立方厘米的水溢出。
22.(1)785升
(2)392.5平方分米
【分析】(1)根据圆柱的容积公式:容积=底面积×高,代入数据,求出蓄水桶的容积,注意单位名数的换算;
(2)求需要铁皮的面积,就是求这个圆柱形蓄水桶的表面积,因为是无盖,需要铁皮的面积=圆柱的表面积=底面积+侧面积;代入数据,即可解答。
【详解】(1)3.14×52×10
=3.14×25×10
=78.5×10
=785(立方分米)
785立方分米=785升
答:这个蓄水桶最多可以装水785升。
(2)3.14×52+3.14×5×2×10
=3.14×25+15.7×2×10
=78.5+31.4×10
=78.5+314
=392.5(平方分米)
答:做一个这样无盖蓄水桶,需要铁皮392.5平方分米。
23.9.42厘米
【分析】根据圆锥的体积公式:体积=底面积×高×,代入数据,求出圆锥的体积,圆锥铁块熔铸成长方体,体积不变,用圆锥的体积除以长方体的宽,再除以长方体的高,即可求出长方体的长。
【详解】3.14×32×20×÷5÷4
=3.14×9×20×÷5÷4
=28.26×20×÷5÷4
=565.2×÷5÷4
=188.4÷5÷4
=37.68÷4
=9.42(厘米)
答:长方体的长是9.42厘米。
24.(1)31.4厘米(2)1177.5毫升
【分析】(1)装饰带的长就是圆柱的底面周长,根据圆的周长C=πd,代入数据计算,即可求出这条装饰带长至少是多少厘米。
(2)根据圆柱的体积=底面积×高,代入数据计算,即可求出这个茶杯的容积。据此解答。
【详解】(1)10×3.14=31.4(厘米)
答:长至少是31.4厘米。
(2)10÷2=5(厘米)
3.14×52×15
=3.14×25×15
=1177.5(立方厘米)
1177.5立方厘米=1177.5毫升
答:这个茶杯的容积大约是1177.5毫升。
25.3.14平方米;188.4元
【分析】这堆沙子的占地面积,就是圆锥形沙堆的底面积,根据圆的面积公式:S=,代入数据解答即可;根据圆锥的体积=底面积×高÷3,求出圆锥形沙堆的体积,再用体积乘每立方米沙子的钱数即可解答。
【详解】2÷2=1(米)
3.14×=3.14(平方米)
3.14×1.5÷3×120
=4.71÷3×120
=1.57×120
=188.4(元)
答:这堆沙子的占地面积是3.14平方米,李叔叔买这堆沙子需要花188.4元。
26.1402.4平方厘米
【分析】根据题意,这种“博士帽”的上面是正方形,下面是无盖无底的圆柱,所以制作一顶“博士帽”至少需要卡纸的面积=正方形的面积+圆柱的侧面积;根据正方形的面积公式S=a2,圆柱的侧面积公式S=πdh,代入数据计算,求出制作一顶“博士帽”至少需要卡纸的面积。
【详解】3.14×16×10+30×30
=50.24×10+900
=502.4+900
=1402.4(平方厘米)
答:制作这样的一顶“博士帽”至少需要1402.4平方厘米的黑色卡纸。
27.18.84立方分米
【分析】这个整流置模型的体积等于底面直径是2分米,高是5分米的圆柱的体积加上底面直径是2分米,高是(8-5)分米的圆锥的体积,根据圆柱的体积公式:体积=底面积×高,圆锥的体积公式:体积=底面积×高×,代入数据,即可解答。
【详解】3.14×(2÷2)2×5+3.14×(2÷2)2×(8-5)×
=3.14×12×5+3.14×12×3×
=3.14×1×5+3.14×1×3×
=3.14×5+3.14×3×
=15.7+9.42×
=15.7+3.14
=18.84(立方分米)
答:这个整流置模型的体积是18.84立方分米。
28.27厘米
【分析】根据题意,把圆锥形钢材从水中完全取出后桶里的水面下降了1厘米,那么水下降的体积等于这个圆锥形钢材的体积;水下降部分是一个底面半径为30厘米、高1厘米的圆柱体,根据圆柱的体积公式V=πr2h,求出水下降部分的体积,也就是圆锥的体积;
已知圆锥形钢材的底面半径为10厘米,根据圆的面积公式S=πr2,求出钢材的底面积;再根据圆锥的高h=3V÷S,求出这个圆锥形钢材的高。
【详解】水下降部分的体积(圆锥的体积):
3.14×302×1
=3.14×900×1
=2826(立方厘米)
圆锥的底面积:
3.14×102
=3.14×100
=314(平方厘米)
圆锥的高:
2826×3÷314
=8478÷314
=27(厘米)
答:这个圆锥形钢材的高是27厘米。
29.(1)卷纸的高
(2)14.13米
【分析】(1)计算卷纸拉开究竟有多长,不需要知道卷纸的高,即不用测量的数据是卷纸的高。
(2)卷纸拉开底面由圆转化成长方形,长方形的面积=底面积,长方形的宽=卷纸的厚度,长方形的长就是卷纸拉开后的长度,根据圆的面积=圆周率×半径的平方,求出底面积,即长方形面积,根据长方形的长=面积÷宽,即可求出卷纸拉开后的长度。
【详解】(1)不用测量的这个数据是卷纸的高。
(2)6÷2=3(厘米)
(厘米)
答:卷纸拉开后长度是14.13米。
30.(1)200.96千克
(2)455.3平方分米
【分析】(1)漏斗的容积=圆柱的容积+圆锥的容积,圆柱的容积=底面积×高,圆锥的容积=底面积×高÷3,据此求出漏斗的容积,漏斗的容积×每立方分米油菜籽的质量=漏斗最多装的油菜籽质量。
(2)防尘罩没有下底面,防尘罩的表面积=底面积+侧面积,侧面积=底面周长×高,据此列式解答。
【详解】(1)3.14×42×6+3.14×42×6÷3
=3.14×16×6+3.14×16×6÷3
=301.44+100.48
=401.92(立方分米)
401.92×0.5=200.96(千克)
答:这个漏斗最多能装200.96千克油菜籽。
(2)3.14×(10÷2)2+3.14×10×12
=3.14×52+376.8
=3.14×25+376.8
=78.5+376.8
=455.3(平方分米)
答:至少需要455.3平方分米铁皮。
