北师大版六年级下册数学期中应用题训练(含解析)
文档属性
| 名称 | 北师大版六年级下册数学期中应用题训练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 603.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 07:58:03 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
北师大版六年级下册数学期中应用题训练
1.青东小学一年级同学参加阳光体育大课间活动比赛,每行站20人,正好站18行,如果每行站24人,可以站多少行?(用比例知识解)
2.发电厂运来一批煤,计划每天烧6吨,可以烧54天。实际每天比计划节约10%,这批煤实际可以烧多少天?
3.一块长12.56分米、宽10分米的长方形铁皮,以宽为高,将长方形铁皮卷成一个圆柱形水桶的侧面,再配一个底面,制成一个水桶,这个水桶的客积是多少升?(铁皮厚度、接口处均忽略不计)
4.2023年9月28日,我国首条设计时速为350千米/小时的跨海高铁——福厦高铁正式开通运营。福厦高铁北起福州,南至厦门和漳州,全长277千米,是我国“八纵八横”高速铁路网中沿海通道的重要组成部分。若把这条跨海高铁画在比例尺是1∶5000000的地图上,应画多少厘米?
5.在一只底面半径是30厘米,高50厘米的圆柱形水桶里,装有水和一个半径为10厘米的圆锥形钢材(钢材完全浸没在水中),如果把钢材从水中完全取出后桶里的水面下降了1厘米,这个圆锥形钢材的高是多少厘米?
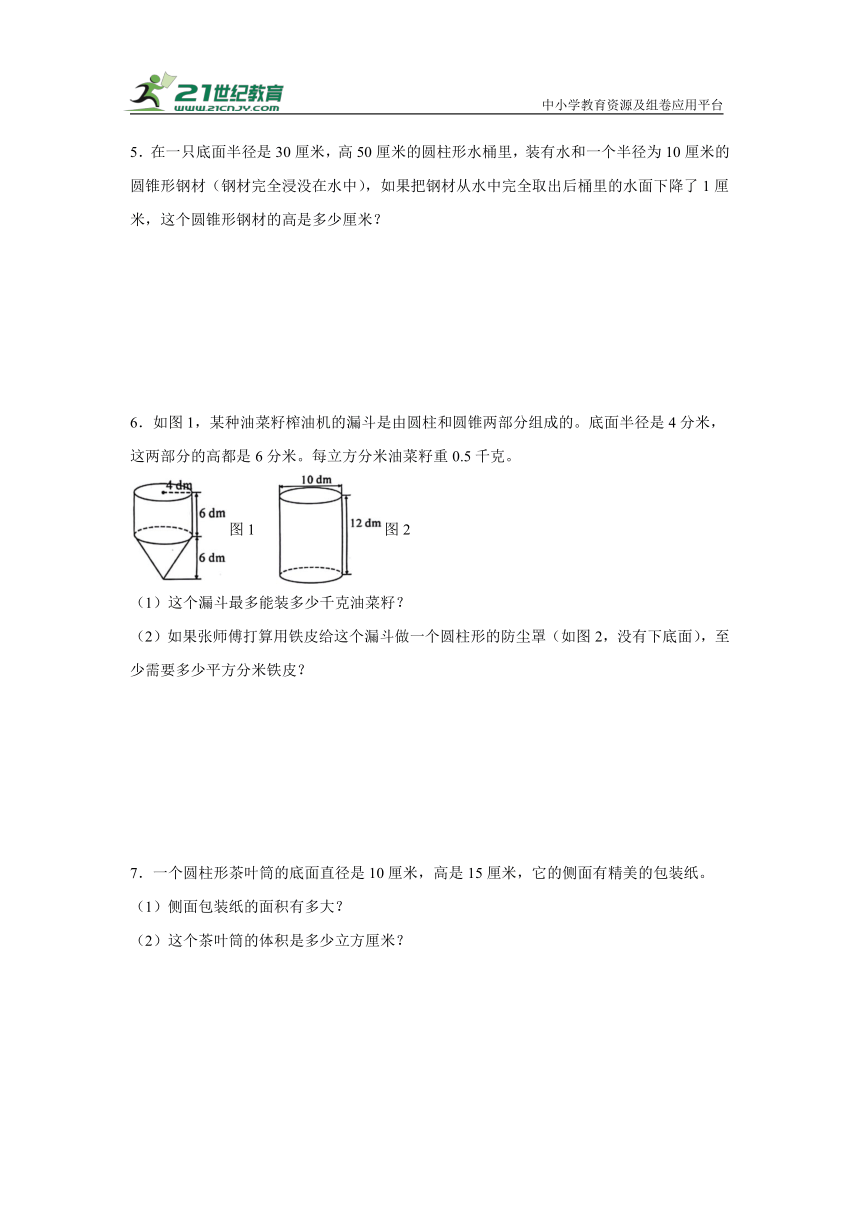
6.如图1,某种油菜籽榨油机的漏斗是由圆柱和圆锥两部分组成的。底面半径是4分米,这两部分的高都是6分米。每立方分米油菜籽重0.5千克。
图1 图2
(1)这个漏斗最多能装多少千克油菜籽?
(2)如果张师傅打算用铁皮给这个漏斗做一个圆柱形的防尘罩(如图2,没有下底面),至少需要多少平方分米铁皮?
7.一个圆柱形茶叶筒的底面直径是10厘米,高是15厘米,它的侧面有精美的包装纸。
(1)侧面包装纸的面积有多大?
(2)这个茶叶筒的体积是多少立方厘米?
8.A、B两地相距800千米,将这两地在比例尺为1∶20000000的地图上标出来。A、B两地间的图上距离是多少?
9.在比例尺为1∶5000000的地图上,量得甲地到乙地的距离是4厘米,一辆货车从甲地出发,每小时行驶50千米,几小时可以到达乙地?
10.一块三角形的钢板,用1∶200的比例画在纸上,两条直角边共长5.4厘米,它们的长度之比是5∶4,这块钢板的实际面积是多少平方米?
11.在一个底面半径为1分米的圆柱形杯里装满水,一个底面半径为5厘米的圆锥形铅锤浸没在水里,当铅锤从水中取出后,杯里的水面下降了5厘米,这个铅锤的体积是多少立方厘米?
12.如图是两个相互啮合的齿轮,它们在同一时间内转动时,大齿轮与小齿轮转过的总齿数是相同的。大齿轮有34个齿,小齿轮有24个齿。当大齿轮每分钟转60圈时,小齿轮每分钟转多少圈?
13.一个圆柱形水桶,底面直径是2分米,高是3分米。若水桶装满水后再放入一个和圆柱等底等高的圆锥形铁块(铁皮厚度忽略不计),桶里还剩多少升水?
14.在直角三角形ABC中,AB=4分米,BC=3分米,如果以AB边为轴旋转一周。
(1)可以得到什么立体图形?
(2)这个立体图形的底面周长是多少?
(3)这个立体图形的体积是多少?
15.给一间房子的地面铺地砖,用边长50厘米的正方形地砖铺,需要30块。如果改用长30厘米、宽25厘米的长方形地砖铺,需要多少块?(用比例解)
16.一个圆锥形沙堆(如图),底面直径2米,高1.5米。如果用容积是0.3立方米的小车来运,需要运几次才能运完?
17.我校“小小厨艺班”兴趣小组要求每个学生做一个薯片筒。底面直径为10厘米,长为20厘米,制作50个这样的薯片筒,至少需要多大面积的纸板?
18.打一篇稿子,每分打字个数与所需的时间如下表。
(1)每分打字个数和所需时间成什么比例关系?为什么?
每分打字个数(个) 120 100 75 60
所需时间(分) 25 30 40 50
(2)如果每分打150个字,打完这篇稿子需要多少分?
19.一台压路机的滚筒是圆柱形,滚筒的宽是2米,横截面半径是0.5米,滚筒每分滚动10周,滚筒一分压过的路面是多少平方米?
20.2022年第24届冬季奥运会在北京和张家口举办,在一幅比例尺是1∶300000的冬奥会宣传图上,京张高铁全线长58厘米,京张高铁实际全线长多少千米?
21.在比例尺是1∶8000000的地图上,量得两地间的距离是6厘米,客、货两车同时从两地相对开出,3小时后相遇,客、货两车的速度比是3∶2,两车的速度各是多少?
22.一个圆锥形沙堆的底面周长是18.84米,高是2.5米。
(1)这堆沙子有多少立方米?
(2)每立方米沙子售价200元,这堆沙子总价是多少元?
23.一个书架上摆着两层书,如果从上层拿走20%,下层拿走25%后,上下两层剩下的图书数之比为2∶3,已知书架的上层原来有60本书,这个书架的下层原有多少本书?
24.在比例尺是1∶6000000的地图上,量得A、B两地间距离是4厘米,A、B两地间的实际距离是多少千米?
25.一个圆锥形稻谷堆,量得它的底面直径为2米,高为1.5米,它的占地面积是多少平方米?如果每立方米的稻谷重750千克,这堆稻谷共重多少千克?
26.手机积分是通过消费话费金额来获得的,通信公司为了回馈广大用户,开展了手机积分兑换话费的活动,1800积分可换30元话费,2400积分可换40元话费,以此类推。王阿姨共有3300积分,可兑换多少话费呢?(用比例解答)
27.在比例尺是1∶5000000的地图上量得甲、乙两地图上距离是7cm,一辆汽车从甲地到乙地行驶了5小时,这辆汽车平均每小时行多少千米?
28.一张长方形铁皮(下图),剪下图中两个圆及一块长方形,正好可以做成一个底面半径为10厘米的圆柱体,圆柱体铁皮的表面积是多少平方厘米?
29.“人强健,清尊素影,长愿相随”,强健的体魄是人生的基石。炎炎夏季冰激凌总会带给我们清凉的感觉,你知道吗?每毫升的冰激凌约产生6千焦的热量。吃一个冰激凌需要30分钟的运动才能消耗掉这些热量。这个冰激凌大约可以产生多少千焦热量?
30.淘气用下面的方法测量1枚一元硬币的体积。
(1)算一算50枚一元硬币摞起来(如图),它的体积是多少?(π取3来计算,得数保留整数)
(2)1枚一元硬币的体积是多大?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
《北师大版六年级下册数学期中应用题训练》参考答案
1.15行
【分析】总人数固定时,每行人数与行数成反比例。设每行站24人时可站行,根据反比例的定义可知等量关系式:每行24人×行数=每行20人×18,据此列方程并求解。
【详解】解:设每行站24人时可站行。
答:可以站15行。
2.60天
【分析】已知计划每天烧6吨,实际每天比计划节约10%,把计划每天烧煤的吨数看作单位“1”,则实际每天烧煤的吨数是计划的(1-10%),单位“1”已知,则计划每天烧煤的吨数×(1-10%)=实际每天烧煤的吨数;
根据题意可知,这批煤的总吨数不变;即每天烧煤的吨数×烧的天数=煤的总吨数(一定),乘积一定,那么每天烧煤的吨数与烧的天数成反比例关系,据此列出反比例方程,并求解。
【详解】解:设这批煤实际可以烧天。
6×(1-10%)×=6×54
6×0.9×=324
5.4=324
=324÷5.4
=60
答:这批煤实际可以烧60天。
3.125.6升
【分析】因为用一块长12.56分米,宽10分米的长方形铁皮,以宽为高做一个圆柱形水桶侧面,所以圆柱形水桶的底面周长是12.56分米,根据 (是圆的周长,是圆的半径)求出底面半径,再根据圆的面积公式2求出桶底的底面面积;最后再根据圆柱体积(容积)公式,列式求出水桶的容积。
【详解】(分米)
(平方分米)
(立方分米)
125.6立方分米升
答:这个水桶的客积是125.6升。
【点睛】此题主要考查圆柱的底面积和体积的计算方法在实际生活中的应用。
4.5.54厘米
【分析】根据图上距离=实际距离×比例尺,代入数据,即可解答,注意单位名数的换算。
【详解】277千米=27700000厘米
27700000×=5.54(厘米)
答:应画5.54厘米。
5.27厘米
【分析】根据题意,把圆锥形钢材从水中完全取出后桶里的水面下降了1厘米,那么水下降的体积等于这个圆锥形钢材的体积;水下降部分是一个底面半径为30厘米、高1厘米的圆柱体,根据圆柱的体积公式V=πr2h,求出水下降部分的体积,也就是圆锥的体积;
已知圆锥形钢材的底面半径为10厘米,根据圆的面积公式S=πr2,求出钢材的底面积;再根据圆锥的高h=3V÷S,求出这个圆锥形钢材的高。
【详解】水下降部分的体积(圆锥的体积):
3.14×302×1
=3.14×900×1
=2826(立方厘米)
圆锥的底面积:
3.14×102
=3.14×100
=314(平方厘米)
圆锥的高:
2826×3÷314
=8478÷314
=27(厘米)
答:这个圆锥形钢材的高是27厘米。
6.(1)200.96千克
(2)455.3平方分米
【分析】(1)漏斗的容积=圆柱的容积+圆锥的容积,圆柱的容积=底面积×高,圆锥的容积=底面积×高÷3,据此求出漏斗的容积,漏斗的容积×每立方分米油菜籽的质量=漏斗最多装的油菜籽质量。
(2)防尘罩没有下底面,防尘罩的表面积=底面积+侧面积,侧面积=底面周长×高,据此列式解答。
【详解】(1)3.14×42×6+3.14×42×6÷3
=3.14×16×6+3.14×16×6÷3
=301.44+100.48
=401.92(立方分米)
401.92×0.5=200.96(千克)
答:这个漏斗最多能装200.96千克油菜籽。
(2)3.14×(10÷2)2+3.14×10×12
=3.14×52+376.8
=3.14×25+376.8
=78.5+376.8
=455.3(平方分米)
答:至少需要455.3平方分米铁皮。
7.(1)471平方厘米;
(2)1177.5立方厘米
【分析】(1)求侧面包装纸的面积就是求圆柱的侧面积,将数据代入圆柱的侧面积公式:S侧=πdh计算即可;
(2)将数据代入圆柱的体积公式:V=πr2h计算即可。
【详解】(1)3.14×10×15
=31.4×15
=471(平方厘米)
答:侧面包装纸的面积是471平方厘米。
(2)3.14×(10÷2)2×15
=3.14×52×15
=3.14×25×15
=78.5×15
=1177.5(立方厘米)
答:这个茶叶筒的体积是1177.5立方厘米。
8.4厘米
【分析】根据图上距离=实际距离×比例尺,代入数据求解即可。
【详解】800千米=80000000厘米
80000000×=4(厘米)
答:A、B两地间的图上距离是4厘米。
9.4小时
【分析】已知地图的比例尺和甲地到乙地的图上距离,根据“实际距离=图上距离÷比例尺”,以及进率“1千米=100000厘米”,求出甲地到乙地的实际距离;
已知货车每小时行驶50千米,根据“时间=路程÷速度”,即可求出货车从甲地到乙地的时间。
【详解】4÷
=4×5000000
=20000000(厘米)
20000000厘米=200千米
200÷50=4(小时)
答:4小时可以到达乙地。
10.14.4平方米
【分析】两条直角边共长5.4厘米,它们的长度之比是5∶4,说明把一条直角边长度看作5份,另一条直角边长度看作4份,它们长度之和看作10份,据此求出两直角边的图上距离,再根据实际距离=图上距离÷比例尺,求出两直角边的实际长度,最后根据三角形面积公式,求出三角形钢板的实际面积即可。
【详解】底:
(厘米)
=6(米)
高:
(厘米)
=4.8(米)
钢板实际面积:6×4.8÷2
=28.8÷2
=14.4(平方米)
答:这块钢板的实际面积14.4平方米。
【点睛】本题考查比例尺、按比分配,解答本题的关键是掌握按比分配解决问题的方法。
11.1570立方厘米
【分析】由题意知:铅锤取出来后,下降的水的体积就是圆锥的体积;根据圆柱的体积V=Sh可求出下降的水的体积,即铅锤的体积,注意单位换算,据此解答即可。
【详解】1分米=10厘米
铅锤体积:
(立方厘米)
答:这个铅锤的体积是1570立方厘米。
【点睛】本题考查圆柱的体积,解答本题的关键是掌握下降的水的体积就是圆锥的体积。
12.85圈
【分析】根据“在同一时间内转动时,大齿轮与小齿轮转过的总齿数是相同的”,即齿数×齿轮转的圈数=总齿数(一定),积一定,则齿数与齿轮转的圈数成反比例关系,据此列出反比例方程,并求解。
【详解】解:设小齿轮每分钟转圈。
24=34×60
24=2040
=2040÷24
=85
答:小齿轮每分钟转85圈。
13.6.28升
【分析】根据圆柱体积=底面积×高,求出原来水的体积,等底等高的圆柱和圆锥,圆锥体积是圆柱体积的,将原来水的体积看作单位“1”,放入等底等高的圆锥形铁块,桶里剩下的水是原来的(1-),原来水的体积×(1-)=剩下水的体积,据此列式解答。
【详解】3.14×(2÷2)2×3×(1-)
=3.14×12×3×
=3.14×1×3×
=6.28(立方分米)
=6.28(升)
答:桶里还剩6.28升水。
14.(1)圆锥;
(2)18.84分米;
(3)37.68立方分米
【分析】(1)根据对圆锥的认识可知:如果以AB边为轴旋转一周,得到一个底面半径为3分米,高为4分米的圆锥;
(2)由(1)可知:圆锥的底面是一个半径为3分米的圆,代入圆的周长公式:C=2πr即可求出底面周长;
(3)将(1)中数据代入圆锥的体积公式:V=πr2h,计算即可。
【详解】(1)如果以AB边为轴旋转一周得到一个底面半径为3分米,高为4分米的圆锥。
答:可以得到一个圆锥。
(2)3.14×3×2
=9.42×2
=18.84(分米)
答:这个立体图形的底面周长是18.84分米。
(3)×3.14×32×4
=×3.14×9×4
=3.14×(×9×4)
=3.14×12
=37.68(立方分米)
答:这个立体图形的体积是37.68立方分米。
15.100块
【分析】根据每块砖的面积×需要的块数=房子的地面面积(一定)可知:每块砖的面积与需要的块数成反比例关系。设如果改用长30厘米、宽25厘米的长方形地砖铺,需要x块,根据每块砖的面积与需要的块数成反比例关系写出比例求解即可。
【详解】解:设如果改用长30厘米、宽25厘米的长方形地砖铺,需要x块
(30×25)×x=(50×50)×30
750x=2500×30
750x=75000
750x÷750=75000÷750
x=100
答:如果改用长30厘米、宽25厘米的长方形地砖铺,需要100块。
16.6次
【分析】已知圆锥形沙堆的底面直径和高,根据圆锥的体积公式V=πr2h,求出这个沙堆的体积;
已知用容积是0.3立方米的小车来运这个沙堆,用沙堆的体积除以小车的容积,即可求出需要运的次数。注意得数采用“进一法”保留整数。
【详解】×3.14×(2÷2)2×1.5
=×3.14×12×1.5
=×3.14×1×1.5
=1.57(立方米)
1.57÷0.3≈6(次)
答:需要运6次才能运完。
17.39250平方厘米
【分析】根据圆柱的表面积公式:表面积=底面积×2+侧面积,代入数据,求出做一个薯片筒需要纸板的面积,再乘50,即可解答。
【详解】[3.14×(10÷2)2×2+3.14×10×20]×50
=[3.14×52×2+31.4×20]×50
=[3.14×25×2+628]×50
=[78.5×2+628]×50
=[157+628]×50
=785×50
=39250(平方厘米)
答:至少需要39250平方厘米的纸板。
18.(1)反比例;原因见详解
(2)20分
【分析】(1)两种相关联的量,如果它们的比值或商一定,则这两种量成正比例关系;如果它们的乘积一定,则这两种量成反比例关系。据此解答。
(2)由(1)可知,每分打字个数和所需时间成反比例关系。设如果每分打150个字,打完这篇稿子需要x分,则150x=60×50,解出方程即可。
【详解】(1)答:每分打字个数和所需时间成反比例关系。因为120×25=100×30=75×40=60×50=3000(一定),乘积一定,则每分打字个数和所需时间成反比例关系。
(2)解:设打完这篇稿子需要x分。
150x=60×50
150x=3000
x=3000÷150
x=20
答:打完这篇稿子需要20分。
19.62.8平方米
【分析】滚筒滚动一周的面积就是这个圆柱形的侧面积,利用圆柱的侧面积=圆柱的底面周长×宽=,即可求得一周压过的路面面积,每分钟转10周,即乘10即可。
【详解】
(平方米)
6.28×10=62.8(平方米)
答:滚筒一分压过的路面是62.8平方米。
【点睛】
20.174千米
【分析】本题根据实际距离=图上距离÷比例尺,代入数据计算即可,注意单位换算。
【详解】(厘米)
17400000厘米=174千米
答:京张高铁实际全线长174千米。
21.客车:96千米/小时,货车:64千米/小时。
【分析】根据实际距离=图上距离÷比例尺,运用分数的除法计算得出两地的实际距离;客车、货车相向而行,3小时后相遇,即客车行驶距离+货车行驶距离=两地距离,可求出客车、货车的速度之和,客、货两车的速度比是3∶2,根据按比分配原则可得出答案。
【详解】两地实际距离为:
=6×8000000
=48000000(厘米)
=480千米。
客车、货车3小时相遇,则速度和为:(千米/小时)
客、货两车的速度比是3∶2,则客车速度为:
(千米/小时)
货车速度为:
(千米/小时)
答:客车速度是96千米/小时,货车速度是64千米/小时。
22.(1)23.55立方米;(2)4710元
【分析】(1)r=C÷π÷2,现求出底面半径,再根据圆锥的体积公式:V=πr2h,然后代入数据即可求出沙子的体积;
(2)根据单价×数量=总价,用沙子的体积×200即可求出总价。
【详解】(1)3.14×(18.84÷3.14÷2)2×2.5×
=3.14×32×2.5×
=3.14×9×2.5×
=23.55(立方米)
答:这堆沙子有23.55立方米。
(2)23.55×200=4710(元)
答:这堆沙子总价是4710元。
23.96本书
【分析】设这个书架的下层原有x本图书;先把上层原有图书的数量看作单位“1”,从上层拿走20%,还剩下(1-20%),用上层原有图书的数量×(1-20%),求出上层还剩下图书的数量;把下层原有图数的数量看作单位“1”,下层拿走25%,还剩下(1-25%),用下层图书原有的数量×(1-25%),求出剩下的图书的数量;现在上下两层剩下的图书数之比为2∶3,列比例:60×(1-20%)∶x×(1-25%)=2∶3,解比例,即可解答。
【详解】解:设下层原来有x本书。
60×(1-20%)∶(1-25%)x=2∶3
60×80%∶75%x=2∶3
48∶75%x=2∶3
75%x×2=48×3
1.5x=144
x=144÷1.5
x=96
答:这个书架的下层原有96本书。
24.240千米
【分析】要求A、B两地间的实际距离是多少千米,根据“图上距离÷比例尺=实际距离”,代入数值进行解答即可。
【详解】4÷
=4×6000000
=24000000(厘米)
24000000厘米=240千米
答:A、B两地间的实际距离是240千米。
25.3.14平方米;1177.5千克
【分析】已知圆锥形稻谷堆的底面直径和高,根据圆的面积公式S=πr2,求出它的占地面积;
根据圆锥的体积公式V=Sh,求出这堆稻谷的体积;
再用每立方米稻谷的重量乘这堆稻谷的体积,即可求出这堆稻谷的总重量。
【详解】圆锥形稻谷堆的占地面积:
3.14×(2÷2)2
=3.14×12
=3.14(平方米)
圆锥形稻谷堆的体积:
×3.14×1.5=1.57(立方米)
这堆稻谷重:
750×1.57=1177.5(千克)
答:它的占地面积是3.14平方米,这堆稻谷共重1177.5千克。
26.55元
【分析】根据题意可得出,积分∶可兑换的话费=每元话费需要的积分(一定),比值一定,那么积分与可兑换的话费成正比例关系,据此列出正比例方程,并求解。
【详解】解:设可兑换元话费。
=
1800=30×3300
1800=99000
=99000÷1800
=55
答:可兑换55元话费。
27.70千米
【分析】根据比例尺的意义,实际距离=图上距离÷比例尺,注意单位的一致,1千米=100000厘米,运用分数除法计算得出甲乙两地的实际距离。再根据速度=路程÷时间,可计算得出答案。
【详解】甲乙两地相距:(厘米)=350千米
则平均速度为:(千米/小时)
答:这辆汽车平均每小时行70千米。
28.1884平方厘米
【分析】根据圆柱的展开图的特征,圆柱的侧面展开是一个长方形,这个长方形的长等于圆柱的底面周长,宽等于圆柱的高,圆柱的高等于底面直径,再根据圆柱表面积=2πr2+=2πrh,代入数据,把两个数据相加求出圆柱体铁皮的表面积即可。
【详解】3.14×102×2+3.14×2×10×(10×2)
=3.14×100×2+6.28×10×20
=314×2+62.8×20
=628+1256
=1884(平方厘米)
答:圆柱体铁皮的表面积是1884平方厘米。
29.847.8千焦
【分析】根据圆锥的体积公式:体积=底面积×高×,代入数据,求出这个圆锥形冰激凌的体积;再用冰激凌的体积×6,即可解答,注意单位名数的换算。
【详解】3.14×(6÷2)2×15×
=3.14×32×15×
=3.14×9×15×
=28.26×15×
=423.9×
=141.3(立方厘米)
141.3立方厘米=141.3毫升
141.3×6=847.8(千焦)
答:这个冰激凌大约可以产生847.8千焦热量。
30.(1)41立方厘米
(2)0.82立方厘米
【分析】(1)50枚一元硬币摞在一起是一个圆柱体,圆柱的体积V=Sh=πr2h,据此代入数据计算。
(2)1枚一元硬币的体积=50枚硬币的总体积÷硬币的数量50,据此解答。
【详解】(1)3×(2.4÷2)2×9.5
=3×1.44×9.5
=4.32×9.5
≈41(立方厘米)
答:它的体积大约是41厘米。
(2)41÷50=0.82(立方厘米)
答:1枚一元硬币的体积是0.82立方厘米。
中小学教育资源及组卷应用平台
北师大版六年级下册数学期中应用题训练
1.青东小学一年级同学参加阳光体育大课间活动比赛,每行站20人,正好站18行,如果每行站24人,可以站多少行?(用比例知识解)
2.发电厂运来一批煤,计划每天烧6吨,可以烧54天。实际每天比计划节约10%,这批煤实际可以烧多少天?
3.一块长12.56分米、宽10分米的长方形铁皮,以宽为高,将长方形铁皮卷成一个圆柱形水桶的侧面,再配一个底面,制成一个水桶,这个水桶的客积是多少升?(铁皮厚度、接口处均忽略不计)
4.2023年9月28日,我国首条设计时速为350千米/小时的跨海高铁——福厦高铁正式开通运营。福厦高铁北起福州,南至厦门和漳州,全长277千米,是我国“八纵八横”高速铁路网中沿海通道的重要组成部分。若把这条跨海高铁画在比例尺是1∶5000000的地图上,应画多少厘米?
5.在一只底面半径是30厘米,高50厘米的圆柱形水桶里,装有水和一个半径为10厘米的圆锥形钢材(钢材完全浸没在水中),如果把钢材从水中完全取出后桶里的水面下降了1厘米,这个圆锥形钢材的高是多少厘米?
6.如图1,某种油菜籽榨油机的漏斗是由圆柱和圆锥两部分组成的。底面半径是4分米,这两部分的高都是6分米。每立方分米油菜籽重0.5千克。
图1 图2
(1)这个漏斗最多能装多少千克油菜籽?
(2)如果张师傅打算用铁皮给这个漏斗做一个圆柱形的防尘罩(如图2,没有下底面),至少需要多少平方分米铁皮?
7.一个圆柱形茶叶筒的底面直径是10厘米,高是15厘米,它的侧面有精美的包装纸。
(1)侧面包装纸的面积有多大?
(2)这个茶叶筒的体积是多少立方厘米?
8.A、B两地相距800千米,将这两地在比例尺为1∶20000000的地图上标出来。A、B两地间的图上距离是多少?
9.在比例尺为1∶5000000的地图上,量得甲地到乙地的距离是4厘米,一辆货车从甲地出发,每小时行驶50千米,几小时可以到达乙地?
10.一块三角形的钢板,用1∶200的比例画在纸上,两条直角边共长5.4厘米,它们的长度之比是5∶4,这块钢板的实际面积是多少平方米?
11.在一个底面半径为1分米的圆柱形杯里装满水,一个底面半径为5厘米的圆锥形铅锤浸没在水里,当铅锤从水中取出后,杯里的水面下降了5厘米,这个铅锤的体积是多少立方厘米?
12.如图是两个相互啮合的齿轮,它们在同一时间内转动时,大齿轮与小齿轮转过的总齿数是相同的。大齿轮有34个齿,小齿轮有24个齿。当大齿轮每分钟转60圈时,小齿轮每分钟转多少圈?
13.一个圆柱形水桶,底面直径是2分米,高是3分米。若水桶装满水后再放入一个和圆柱等底等高的圆锥形铁块(铁皮厚度忽略不计),桶里还剩多少升水?
14.在直角三角形ABC中,AB=4分米,BC=3分米,如果以AB边为轴旋转一周。
(1)可以得到什么立体图形?
(2)这个立体图形的底面周长是多少?
(3)这个立体图形的体积是多少?
15.给一间房子的地面铺地砖,用边长50厘米的正方形地砖铺,需要30块。如果改用长30厘米、宽25厘米的长方形地砖铺,需要多少块?(用比例解)
16.一个圆锥形沙堆(如图),底面直径2米,高1.5米。如果用容积是0.3立方米的小车来运,需要运几次才能运完?
17.我校“小小厨艺班”兴趣小组要求每个学生做一个薯片筒。底面直径为10厘米,长为20厘米,制作50个这样的薯片筒,至少需要多大面积的纸板?
18.打一篇稿子,每分打字个数与所需的时间如下表。
(1)每分打字个数和所需时间成什么比例关系?为什么?
每分打字个数(个) 120 100 75 60
所需时间(分) 25 30 40 50
(2)如果每分打150个字,打完这篇稿子需要多少分?
19.一台压路机的滚筒是圆柱形,滚筒的宽是2米,横截面半径是0.5米,滚筒每分滚动10周,滚筒一分压过的路面是多少平方米?
20.2022年第24届冬季奥运会在北京和张家口举办,在一幅比例尺是1∶300000的冬奥会宣传图上,京张高铁全线长58厘米,京张高铁实际全线长多少千米?
21.在比例尺是1∶8000000的地图上,量得两地间的距离是6厘米,客、货两车同时从两地相对开出,3小时后相遇,客、货两车的速度比是3∶2,两车的速度各是多少?
22.一个圆锥形沙堆的底面周长是18.84米,高是2.5米。
(1)这堆沙子有多少立方米?
(2)每立方米沙子售价200元,这堆沙子总价是多少元?
23.一个书架上摆着两层书,如果从上层拿走20%,下层拿走25%后,上下两层剩下的图书数之比为2∶3,已知书架的上层原来有60本书,这个书架的下层原有多少本书?
24.在比例尺是1∶6000000的地图上,量得A、B两地间距离是4厘米,A、B两地间的实际距离是多少千米?
25.一个圆锥形稻谷堆,量得它的底面直径为2米,高为1.5米,它的占地面积是多少平方米?如果每立方米的稻谷重750千克,这堆稻谷共重多少千克?
26.手机积分是通过消费话费金额来获得的,通信公司为了回馈广大用户,开展了手机积分兑换话费的活动,1800积分可换30元话费,2400积分可换40元话费,以此类推。王阿姨共有3300积分,可兑换多少话费呢?(用比例解答)
27.在比例尺是1∶5000000的地图上量得甲、乙两地图上距离是7cm,一辆汽车从甲地到乙地行驶了5小时,这辆汽车平均每小时行多少千米?
28.一张长方形铁皮(下图),剪下图中两个圆及一块长方形,正好可以做成一个底面半径为10厘米的圆柱体,圆柱体铁皮的表面积是多少平方厘米?
29.“人强健,清尊素影,长愿相随”,强健的体魄是人生的基石。炎炎夏季冰激凌总会带给我们清凉的感觉,你知道吗?每毫升的冰激凌约产生6千焦的热量。吃一个冰激凌需要30分钟的运动才能消耗掉这些热量。这个冰激凌大约可以产生多少千焦热量?
30.淘气用下面的方法测量1枚一元硬币的体积。
(1)算一算50枚一元硬币摞起来(如图),它的体积是多少?(π取3来计算,得数保留整数)
(2)1枚一元硬币的体积是多大?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
《北师大版六年级下册数学期中应用题训练》参考答案
1.15行
【分析】总人数固定时,每行人数与行数成反比例。设每行站24人时可站行,根据反比例的定义可知等量关系式:每行24人×行数=每行20人×18,据此列方程并求解。
【详解】解:设每行站24人时可站行。
答:可以站15行。
2.60天
【分析】已知计划每天烧6吨,实际每天比计划节约10%,把计划每天烧煤的吨数看作单位“1”,则实际每天烧煤的吨数是计划的(1-10%),单位“1”已知,则计划每天烧煤的吨数×(1-10%)=实际每天烧煤的吨数;
根据题意可知,这批煤的总吨数不变;即每天烧煤的吨数×烧的天数=煤的总吨数(一定),乘积一定,那么每天烧煤的吨数与烧的天数成反比例关系,据此列出反比例方程,并求解。
【详解】解:设这批煤实际可以烧天。
6×(1-10%)×=6×54
6×0.9×=324
5.4=324
=324÷5.4
=60
答:这批煤实际可以烧60天。
3.125.6升
【分析】因为用一块长12.56分米,宽10分米的长方形铁皮,以宽为高做一个圆柱形水桶侧面,所以圆柱形水桶的底面周长是12.56分米,根据 (是圆的周长,是圆的半径)求出底面半径,再根据圆的面积公式2求出桶底的底面面积;最后再根据圆柱体积(容积)公式,列式求出水桶的容积。
【详解】(分米)
(平方分米)
(立方分米)
125.6立方分米升
答:这个水桶的客积是125.6升。
【点睛】此题主要考查圆柱的底面积和体积的计算方法在实际生活中的应用。
4.5.54厘米
【分析】根据图上距离=实际距离×比例尺,代入数据,即可解答,注意单位名数的换算。
【详解】277千米=27700000厘米
27700000×=5.54(厘米)
答:应画5.54厘米。
5.27厘米
【分析】根据题意,把圆锥形钢材从水中完全取出后桶里的水面下降了1厘米,那么水下降的体积等于这个圆锥形钢材的体积;水下降部分是一个底面半径为30厘米、高1厘米的圆柱体,根据圆柱的体积公式V=πr2h,求出水下降部分的体积,也就是圆锥的体积;
已知圆锥形钢材的底面半径为10厘米,根据圆的面积公式S=πr2,求出钢材的底面积;再根据圆锥的高h=3V÷S,求出这个圆锥形钢材的高。
【详解】水下降部分的体积(圆锥的体积):
3.14×302×1
=3.14×900×1
=2826(立方厘米)
圆锥的底面积:
3.14×102
=3.14×100
=314(平方厘米)
圆锥的高:
2826×3÷314
=8478÷314
=27(厘米)
答:这个圆锥形钢材的高是27厘米。
6.(1)200.96千克
(2)455.3平方分米
【分析】(1)漏斗的容积=圆柱的容积+圆锥的容积,圆柱的容积=底面积×高,圆锥的容积=底面积×高÷3,据此求出漏斗的容积,漏斗的容积×每立方分米油菜籽的质量=漏斗最多装的油菜籽质量。
(2)防尘罩没有下底面,防尘罩的表面积=底面积+侧面积,侧面积=底面周长×高,据此列式解答。
【详解】(1)3.14×42×6+3.14×42×6÷3
=3.14×16×6+3.14×16×6÷3
=301.44+100.48
=401.92(立方分米)
401.92×0.5=200.96(千克)
答:这个漏斗最多能装200.96千克油菜籽。
(2)3.14×(10÷2)2+3.14×10×12
=3.14×52+376.8
=3.14×25+376.8
=78.5+376.8
=455.3(平方分米)
答:至少需要455.3平方分米铁皮。
7.(1)471平方厘米;
(2)1177.5立方厘米
【分析】(1)求侧面包装纸的面积就是求圆柱的侧面积,将数据代入圆柱的侧面积公式:S侧=πdh计算即可;
(2)将数据代入圆柱的体积公式:V=πr2h计算即可。
【详解】(1)3.14×10×15
=31.4×15
=471(平方厘米)
答:侧面包装纸的面积是471平方厘米。
(2)3.14×(10÷2)2×15
=3.14×52×15
=3.14×25×15
=78.5×15
=1177.5(立方厘米)
答:这个茶叶筒的体积是1177.5立方厘米。
8.4厘米
【分析】根据图上距离=实际距离×比例尺,代入数据求解即可。
【详解】800千米=80000000厘米
80000000×=4(厘米)
答:A、B两地间的图上距离是4厘米。
9.4小时
【分析】已知地图的比例尺和甲地到乙地的图上距离,根据“实际距离=图上距离÷比例尺”,以及进率“1千米=100000厘米”,求出甲地到乙地的实际距离;
已知货车每小时行驶50千米,根据“时间=路程÷速度”,即可求出货车从甲地到乙地的时间。
【详解】4÷
=4×5000000
=20000000(厘米)
20000000厘米=200千米
200÷50=4(小时)
答:4小时可以到达乙地。
10.14.4平方米
【分析】两条直角边共长5.4厘米,它们的长度之比是5∶4,说明把一条直角边长度看作5份,另一条直角边长度看作4份,它们长度之和看作10份,据此求出两直角边的图上距离,再根据实际距离=图上距离÷比例尺,求出两直角边的实际长度,最后根据三角形面积公式,求出三角形钢板的实际面积即可。
【详解】底:
(厘米)
=6(米)
高:
(厘米)
=4.8(米)
钢板实际面积:6×4.8÷2
=28.8÷2
=14.4(平方米)
答:这块钢板的实际面积14.4平方米。
【点睛】本题考查比例尺、按比分配,解答本题的关键是掌握按比分配解决问题的方法。
11.1570立方厘米
【分析】由题意知:铅锤取出来后,下降的水的体积就是圆锥的体积;根据圆柱的体积V=Sh可求出下降的水的体积,即铅锤的体积,注意单位换算,据此解答即可。
【详解】1分米=10厘米
铅锤体积:
(立方厘米)
答:这个铅锤的体积是1570立方厘米。
【点睛】本题考查圆柱的体积,解答本题的关键是掌握下降的水的体积就是圆锥的体积。
12.85圈
【分析】根据“在同一时间内转动时,大齿轮与小齿轮转过的总齿数是相同的”,即齿数×齿轮转的圈数=总齿数(一定),积一定,则齿数与齿轮转的圈数成反比例关系,据此列出反比例方程,并求解。
【详解】解:设小齿轮每分钟转圈。
24=34×60
24=2040
=2040÷24
=85
答:小齿轮每分钟转85圈。
13.6.28升
【分析】根据圆柱体积=底面积×高,求出原来水的体积,等底等高的圆柱和圆锥,圆锥体积是圆柱体积的,将原来水的体积看作单位“1”,放入等底等高的圆锥形铁块,桶里剩下的水是原来的(1-),原来水的体积×(1-)=剩下水的体积,据此列式解答。
【详解】3.14×(2÷2)2×3×(1-)
=3.14×12×3×
=3.14×1×3×
=6.28(立方分米)
=6.28(升)
答:桶里还剩6.28升水。
14.(1)圆锥;
(2)18.84分米;
(3)37.68立方分米
【分析】(1)根据对圆锥的认识可知:如果以AB边为轴旋转一周,得到一个底面半径为3分米,高为4分米的圆锥;
(2)由(1)可知:圆锥的底面是一个半径为3分米的圆,代入圆的周长公式:C=2πr即可求出底面周长;
(3)将(1)中数据代入圆锥的体积公式:V=πr2h,计算即可。
【详解】(1)如果以AB边为轴旋转一周得到一个底面半径为3分米,高为4分米的圆锥。
答:可以得到一个圆锥。
(2)3.14×3×2
=9.42×2
=18.84(分米)
答:这个立体图形的底面周长是18.84分米。
(3)×3.14×32×4
=×3.14×9×4
=3.14×(×9×4)
=3.14×12
=37.68(立方分米)
答:这个立体图形的体积是37.68立方分米。
15.100块
【分析】根据每块砖的面积×需要的块数=房子的地面面积(一定)可知:每块砖的面积与需要的块数成反比例关系。设如果改用长30厘米、宽25厘米的长方形地砖铺,需要x块,根据每块砖的面积与需要的块数成反比例关系写出比例求解即可。
【详解】解:设如果改用长30厘米、宽25厘米的长方形地砖铺,需要x块
(30×25)×x=(50×50)×30
750x=2500×30
750x=75000
750x÷750=75000÷750
x=100
答:如果改用长30厘米、宽25厘米的长方形地砖铺,需要100块。
16.6次
【分析】已知圆锥形沙堆的底面直径和高,根据圆锥的体积公式V=πr2h,求出这个沙堆的体积;
已知用容积是0.3立方米的小车来运这个沙堆,用沙堆的体积除以小车的容积,即可求出需要运的次数。注意得数采用“进一法”保留整数。
【详解】×3.14×(2÷2)2×1.5
=×3.14×12×1.5
=×3.14×1×1.5
=1.57(立方米)
1.57÷0.3≈6(次)
答:需要运6次才能运完。
17.39250平方厘米
【分析】根据圆柱的表面积公式:表面积=底面积×2+侧面积,代入数据,求出做一个薯片筒需要纸板的面积,再乘50,即可解答。
【详解】[3.14×(10÷2)2×2+3.14×10×20]×50
=[3.14×52×2+31.4×20]×50
=[3.14×25×2+628]×50
=[78.5×2+628]×50
=[157+628]×50
=785×50
=39250(平方厘米)
答:至少需要39250平方厘米的纸板。
18.(1)反比例;原因见详解
(2)20分
【分析】(1)两种相关联的量,如果它们的比值或商一定,则这两种量成正比例关系;如果它们的乘积一定,则这两种量成反比例关系。据此解答。
(2)由(1)可知,每分打字个数和所需时间成反比例关系。设如果每分打150个字,打完这篇稿子需要x分,则150x=60×50,解出方程即可。
【详解】(1)答:每分打字个数和所需时间成反比例关系。因为120×25=100×30=75×40=60×50=3000(一定),乘积一定,则每分打字个数和所需时间成反比例关系。
(2)解:设打完这篇稿子需要x分。
150x=60×50
150x=3000
x=3000÷150
x=20
答:打完这篇稿子需要20分。
19.62.8平方米
【分析】滚筒滚动一周的面积就是这个圆柱形的侧面积,利用圆柱的侧面积=圆柱的底面周长×宽=,即可求得一周压过的路面面积,每分钟转10周,即乘10即可。
【详解】
(平方米)
6.28×10=62.8(平方米)
答:滚筒一分压过的路面是62.8平方米。
【点睛】
20.174千米
【分析】本题根据实际距离=图上距离÷比例尺,代入数据计算即可,注意单位换算。
【详解】(厘米)
17400000厘米=174千米
答:京张高铁实际全线长174千米。
21.客车:96千米/小时,货车:64千米/小时。
【分析】根据实际距离=图上距离÷比例尺,运用分数的除法计算得出两地的实际距离;客车、货车相向而行,3小时后相遇,即客车行驶距离+货车行驶距离=两地距离,可求出客车、货车的速度之和,客、货两车的速度比是3∶2,根据按比分配原则可得出答案。
【详解】两地实际距离为:
=6×8000000
=48000000(厘米)
=480千米。
客车、货车3小时相遇,则速度和为:(千米/小时)
客、货两车的速度比是3∶2,则客车速度为:
(千米/小时)
货车速度为:
(千米/小时)
答:客车速度是96千米/小时,货车速度是64千米/小时。
22.(1)23.55立方米;(2)4710元
【分析】(1)r=C÷π÷2,现求出底面半径,再根据圆锥的体积公式:V=πr2h,然后代入数据即可求出沙子的体积;
(2)根据单价×数量=总价,用沙子的体积×200即可求出总价。
【详解】(1)3.14×(18.84÷3.14÷2)2×2.5×
=3.14×32×2.5×
=3.14×9×2.5×
=23.55(立方米)
答:这堆沙子有23.55立方米。
(2)23.55×200=4710(元)
答:这堆沙子总价是4710元。
23.96本书
【分析】设这个书架的下层原有x本图书;先把上层原有图书的数量看作单位“1”,从上层拿走20%,还剩下(1-20%),用上层原有图书的数量×(1-20%),求出上层还剩下图书的数量;把下层原有图数的数量看作单位“1”,下层拿走25%,还剩下(1-25%),用下层图书原有的数量×(1-25%),求出剩下的图书的数量;现在上下两层剩下的图书数之比为2∶3,列比例:60×(1-20%)∶x×(1-25%)=2∶3,解比例,即可解答。
【详解】解:设下层原来有x本书。
60×(1-20%)∶(1-25%)x=2∶3
60×80%∶75%x=2∶3
48∶75%x=2∶3
75%x×2=48×3
1.5x=144
x=144÷1.5
x=96
答:这个书架的下层原有96本书。
24.240千米
【分析】要求A、B两地间的实际距离是多少千米,根据“图上距离÷比例尺=实际距离”,代入数值进行解答即可。
【详解】4÷
=4×6000000
=24000000(厘米)
24000000厘米=240千米
答:A、B两地间的实际距离是240千米。
25.3.14平方米;1177.5千克
【分析】已知圆锥形稻谷堆的底面直径和高,根据圆的面积公式S=πr2,求出它的占地面积;
根据圆锥的体积公式V=Sh,求出这堆稻谷的体积;
再用每立方米稻谷的重量乘这堆稻谷的体积,即可求出这堆稻谷的总重量。
【详解】圆锥形稻谷堆的占地面积:
3.14×(2÷2)2
=3.14×12
=3.14(平方米)
圆锥形稻谷堆的体积:
×3.14×1.5=1.57(立方米)
这堆稻谷重:
750×1.57=1177.5(千克)
答:它的占地面积是3.14平方米,这堆稻谷共重1177.5千克。
26.55元
【分析】根据题意可得出,积分∶可兑换的话费=每元话费需要的积分(一定),比值一定,那么积分与可兑换的话费成正比例关系,据此列出正比例方程,并求解。
【详解】解:设可兑换元话费。
=
1800=30×3300
1800=99000
=99000÷1800
=55
答:可兑换55元话费。
27.70千米
【分析】根据比例尺的意义,实际距离=图上距离÷比例尺,注意单位的一致,1千米=100000厘米,运用分数除法计算得出甲乙两地的实际距离。再根据速度=路程÷时间,可计算得出答案。
【详解】甲乙两地相距:(厘米)=350千米
则平均速度为:(千米/小时)
答:这辆汽车平均每小时行70千米。
28.1884平方厘米
【分析】根据圆柱的展开图的特征,圆柱的侧面展开是一个长方形,这个长方形的长等于圆柱的底面周长,宽等于圆柱的高,圆柱的高等于底面直径,再根据圆柱表面积=2πr2+=2πrh,代入数据,把两个数据相加求出圆柱体铁皮的表面积即可。
【详解】3.14×102×2+3.14×2×10×(10×2)
=3.14×100×2+6.28×10×20
=314×2+62.8×20
=628+1256
=1884(平方厘米)
答:圆柱体铁皮的表面积是1884平方厘米。
29.847.8千焦
【分析】根据圆锥的体积公式:体积=底面积×高×,代入数据,求出这个圆锥形冰激凌的体积;再用冰激凌的体积×6,即可解答,注意单位名数的换算。
【详解】3.14×(6÷2)2×15×
=3.14×32×15×
=3.14×9×15×
=28.26×15×
=423.9×
=141.3(立方厘米)
141.3立方厘米=141.3毫升
141.3×6=847.8(千焦)
答:这个冰激凌大约可以产生847.8千焦热量。
30.(1)41立方厘米
(2)0.82立方厘米
【分析】(1)50枚一元硬币摞在一起是一个圆柱体,圆柱的体积V=Sh=πr2h,据此代入数据计算。
(2)1枚一元硬币的体积=50枚硬币的总体积÷硬币的数量50,据此解答。
【详解】(1)3×(2.4÷2)2×9.5
=3×1.44×9.5
=4.32×9.5
≈41(立方厘米)
答:它的体积大约是41厘米。
(2)41÷50=0.82(立方厘米)
答:1枚一元硬币的体积是0.82立方厘米。
同课章节目录
