北师大版五年级下册数学第四单元长方体(二)图形计算题训练(含解析)
文档属性
| 名称 | 北师大版五年级下册数学第四单元长方体(二)图形计算题训练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 08:07:42 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
北师大版五年级下册数学第四单元长方体(二)图形计算题训练
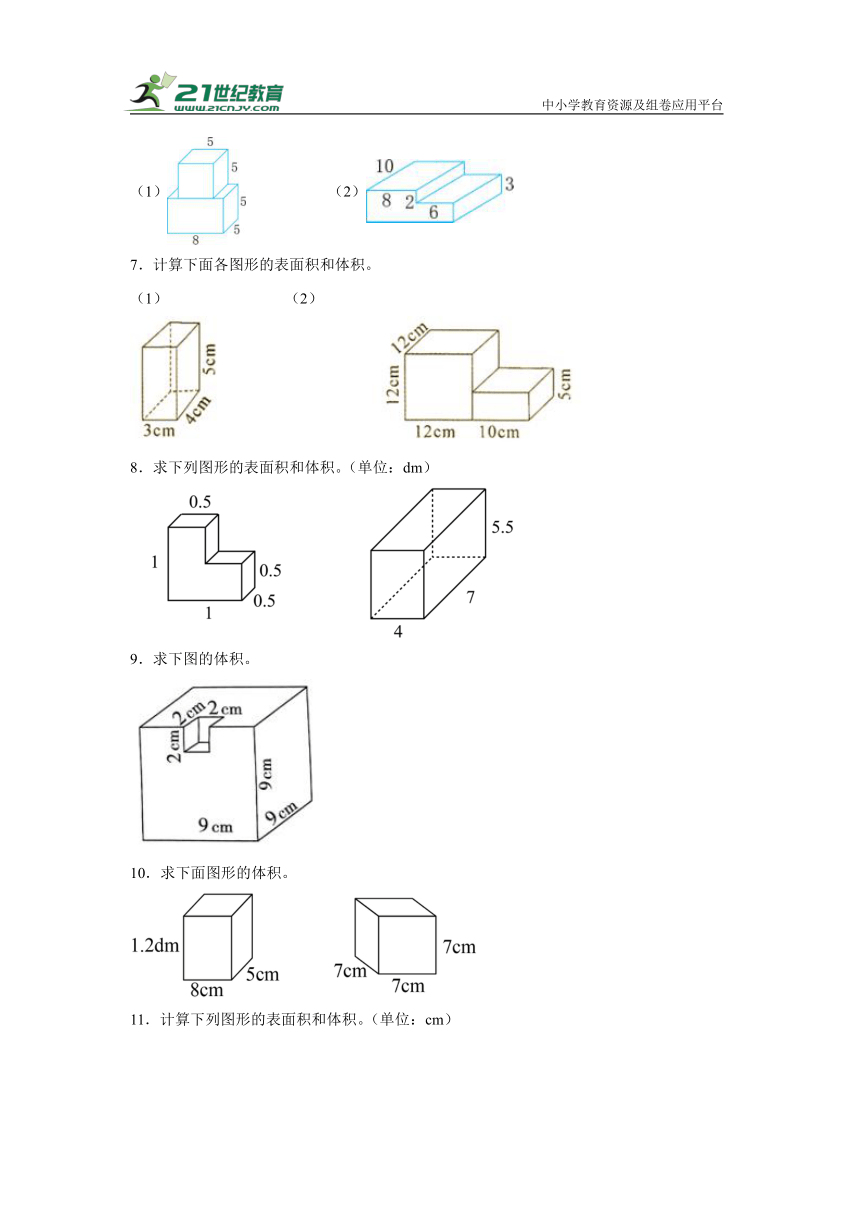
1.计算下面各图形的体积。(单位:厘米)
2.计算下面立体图形的表面积和体积。(单位:cm)
3.计算下图中空心砖的体积。(单位:分米)
4.下图是长方体的展开图,求出这个长方体的表面积和体积。
5.计算下面立体图形的表面积和体积。
6.求下面各立体图形的体积。(单位:cm)
(1) (2)
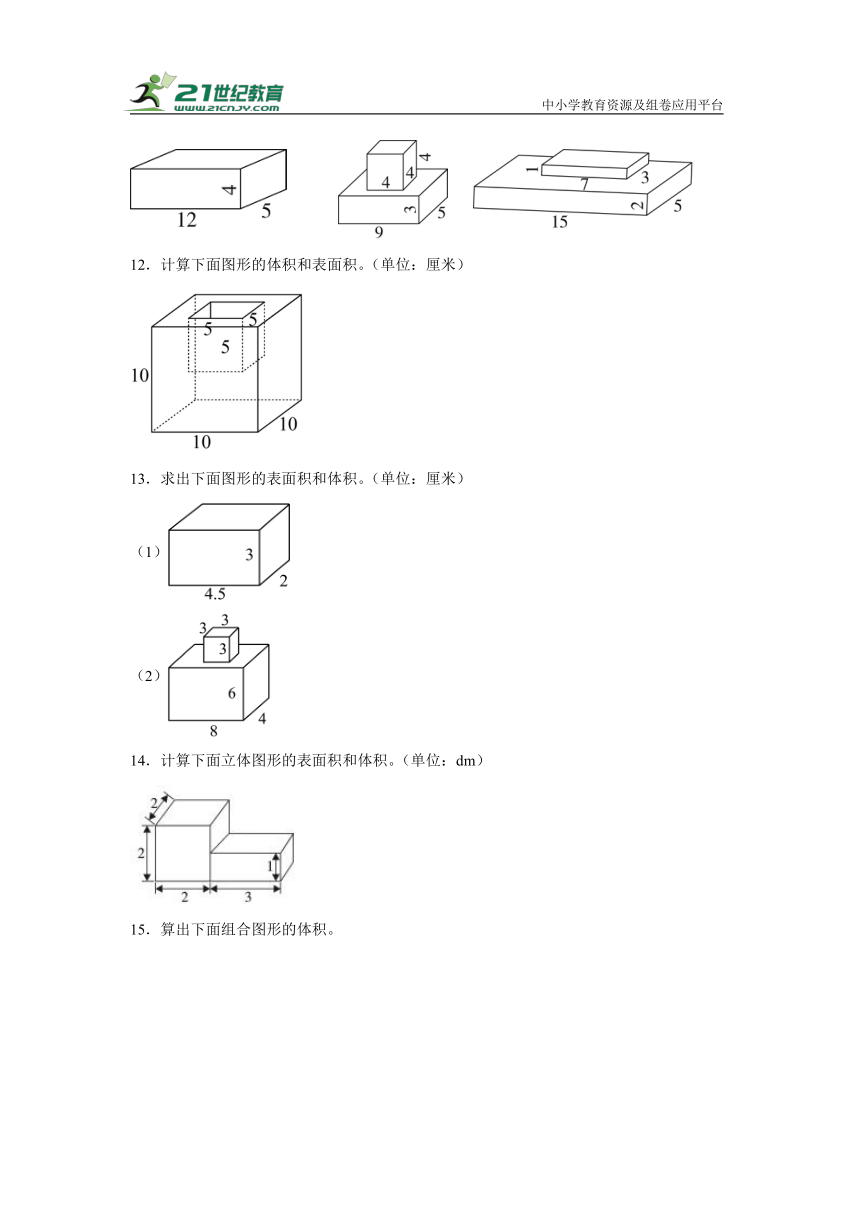
7.计算下面各图形的表面积和体积。
(1) (2)
8.求下列图形的表面积和体积。(单位:dm)
9.求下图的体积。
10.求下面图形的体积。
11.计算下列图形的表面积和体积。(单位:cm)
12.计算下面图形的体积和表面积。(单位:厘米)
13.求出下面图形的表面积和体积。(单位:厘米)
(1)
(2)
14.计算下面立体图形的表面积和体积。(单位:dm)
15.算出下面组合图形的体积。
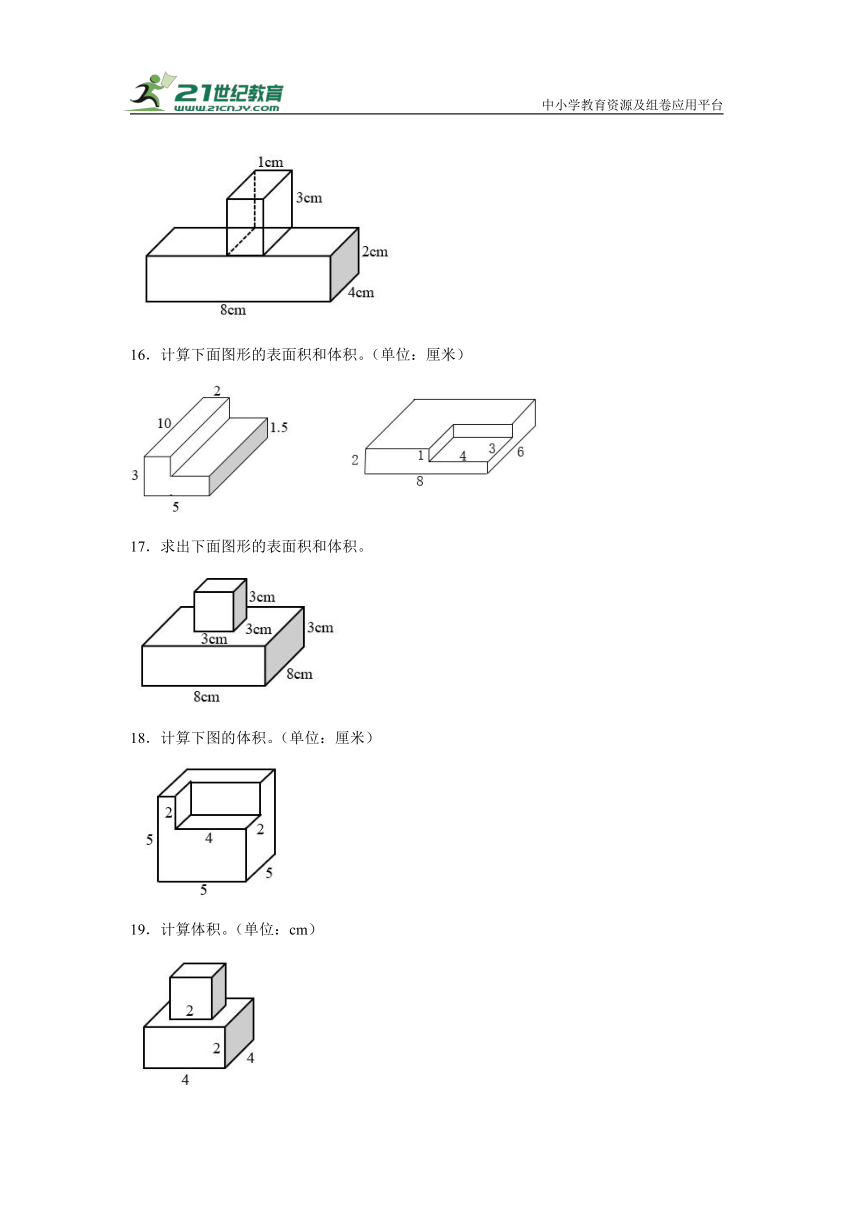
16.计算下面图形的表面积和体积。(单位:厘米)
17.求出下面图形的表面积和体积。
18.计算下图的体积。(单位:厘米)
19.计算体积。(单位:cm)
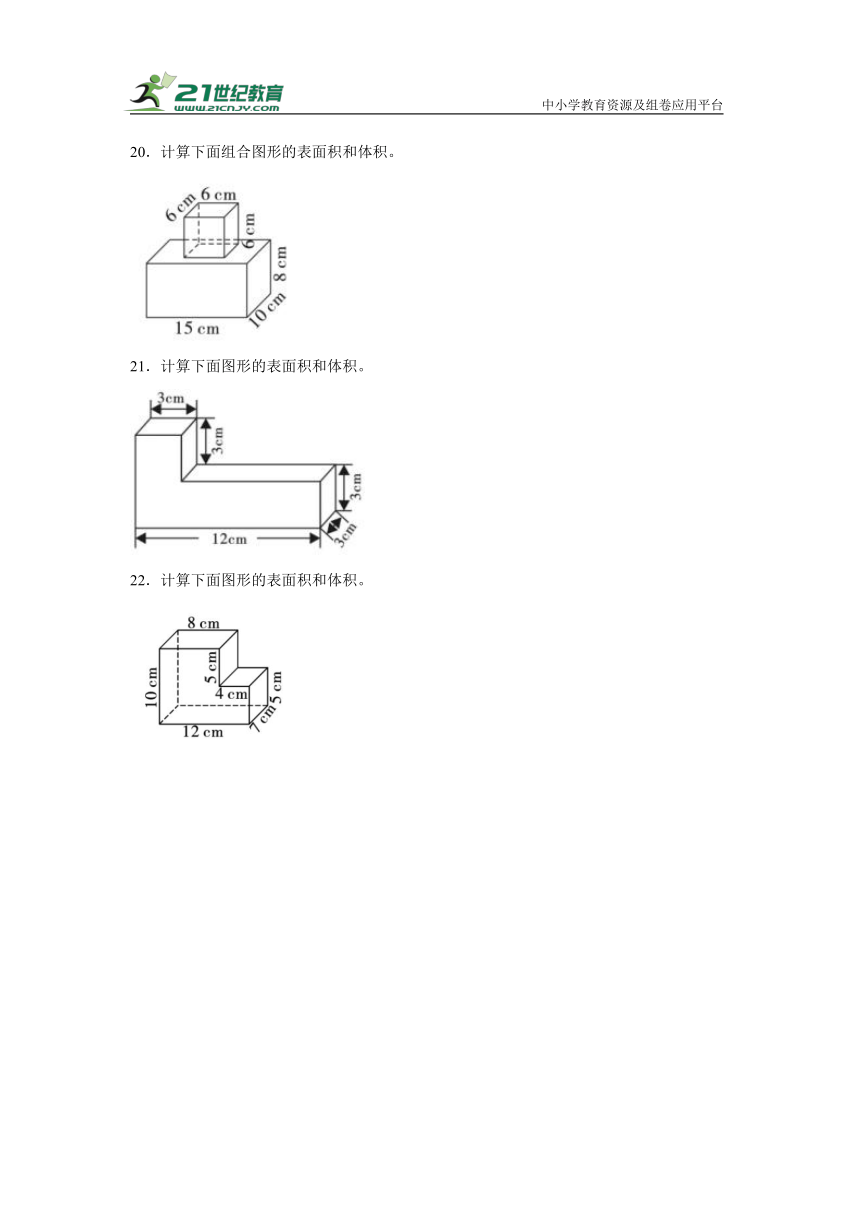
20.计算下面组合图形的表面积和体积。
21.计算下面图形的表面积和体积。
22.计算下面图形的表面积和体积。
《北师大版五年级下册数学第四单元长方体(二)图形计算题训练》参考答案
1.512立方厘米;1080立方厘米
【分析】由图一可知,正方体的棱长是8厘米,根据正方体的体积=棱长×棱长×棱长,将棱长代入公式即可求出正方体的体积;
由图二可知,长方体的长是15厘米,宽是8厘米,高是9厘米,长方体的体积=长×宽×高,将长、宽、高的数据代入公式计算即可解答。
【详解】正方体的体积:
8×8×8
=64×8
=512(立方厘米)
长方体的体积:
15×8×9
=120×9
=1080(立方厘米)
2.224cm2;208cm3
【分析】通过平移的知识可以发现,立体图形的表面积比棱长为6cm的正方体的表面积多了2个边长为2cm的正方形的面积,根据正方体的表面积=棱长×棱长×6,正方形的面积=边长×边长,代入数据计算即可;立体图形的体积=大正方体的体积-小正方体的体积,根据正方体的体积=棱长×棱长×棱长即可解答。
【详解】6×6×6+2×2×2
=36×6+4×2
=216+8
=224(cm2)
6×6×6-2×2×2
=36×6-4×2
=216-8
=208(cm3)
立体图形的表面积是224cm2,体积是208cm3。
3.27.5立方分米
【分析】根据长方体的体积=长×宽×高,分别求出外面大长方体的体积和内部挖掉的小长方体体积,再用减法求出差,即可得空心砖的体积。
【详解】4×2.5×3-1×1×2.5
=30-2.5
=27.5(立方分米)
这个空心砖的体积是27.5立方分米。
4.表面积:158平方分米;体积:120立方分米
【分析】观察图形可知,长方体的长是8分米,宽是5分米,高是3分米;根据长方体表面积=(长×宽+长×高+宽×高)×2,长方体体=长×宽×高,代入数据,即可解答。
【详解】长方体的长是8分米,宽是5分米,高是3分米。
表面积:(8×5+8×3+5×3)×2
=(40+24+15)×2
=(64+15)×2
=79×2
=158(平方分米)
体积:8×5×3
=40×3
=120(立方分米)
长方体的表面积是158平方分米,体积是120立方米。
5.152平方分米;88立方分米
【分析】由图可知:在大长方体的顶点处去掉一个小长方体,虽然体积减少了,但是表面积不变。根据长方体的表面积S=(ab+ah+bh)×2,求出立体图形的表面积。长方体的体积V=abh,用大长方体的体积减去小长方体的体积,求出立体图形的体积。
【详解】立体图形的表面积:
=(48+16+12)×2
=(64+12)×2
=76×2
=152(平方分米)
立体图形的体积:
=48×2-4×2×1
=96-8
=88(立方分米)
图形的表面积是152平方分米,体积是88立方分米。
6.(1)325cm3;(2)580cm3
【分析】(1)观察图形可知,组合图形的体积=正方体的体积+长方体的体积,根据正方体的体积公式V=a3,长方体的体积公式V=abh,代入数据计算求解。
(2)如下图,把组合图形分成左右两部分,那么组合图形的体积=大长方体的体积+小长方体的体积,根据长方体的体积公式V=abh,代入数据计算求解。
【详解】(1)5×5×5+8×5×5
=125+200
=325(cm3)
组合图形的体积是325cm3。
(2)8×10×(2+3)+6×10×3
=8×10×5+180
=400+180
=580(cm3)
组合图形的体积是580cm3。
7.(1)94cm2;60cm3
(2)1204cm2;2328cm3
【分析】(1)根据长方体的表面积公式S=2(ab+ah+bh),长方体的体积公式V=abh,代入数据计算求出长方体的表面积和体积。
(2)如下图,把长方体的右面如箭头所示向左平移,补给正方体的右面,这样正方体的表面积是6个面的面积之和,而长方体的表面积只需计算4个面(上下面和前后面)的面积。
因此组合图形的表面积=正方体的表面积+长方体上下面的面积+长方体前后面的面积;
根据正方体的表面积公式S=6a2,长方体4个面的面积之和公式S=2ab+2ah,代入数据计算求解。
组合图形的体积=正方体的体积+长方体的体积,根据正方体的体积公式V=a3,长方体的体积公式V=abh,代入数据计算求解。
【详解】(1)表面积:
(3×4+3×5+4×5)×2
=(12+15+20)×2
=47×2
=94(cm2)
体积:
3×4×5=60(cm3)
长方体的表面积是94cm2,体积是60cm3。
(2)表面积:
12×12×6+10×12×2+10×5×2
=864+240+100
=1204(cm2)
体积:
12×12×12+10×12×5
=1728+600
=2328(cm3)
组合图形的表面积是1204cm2,体积是2328cm3。
8.3.5dm2,0.375dm3;177dm2,154dm3
【分析】
如图,组合体的表面积=完整的长方体表面积+正方体一个面的面积×4,看图可知,长方体是有2个面是正方形的特殊长方体,前后左右4个面的面积相等,这个长方体表面积=长×宽×2+长×高×4,组合体的体积=长方体体积+正方体体积,长方体体积=长×宽×高,正方体体积=棱长×棱长×棱长;
长方体表面积=(长×宽+长×高+宽×高)×2,长方体体积=长×宽×高,据此列式计算。
【详解】1-0.5=0.5(dm)
0.5×0.5×2+0.5×1×4+0.5×0.5×4
=0.5+2+1
=3.5(dm2)
0.5×0.5×1+0.5×0.5×0.5
=0.25+0.125
=0.375(dm3)
(4×7+4×5.5+7×5.5)×2
=(28+22+38.5)×2
=88.5×2
=177(dm2)
4×7×5.5=154(dm3)
组合体的表面积是3.5dm2,体积是0.375dm3;长方体的表面积是177dm2,体积是154dm3。
9.721cm3
【分析】观察图形可知,图形的体积=大正方体的体积-小正方体的体积,根据正方体的体积公式V=a3,代入数据计算求解。
【详解】9×9×9-2×2×2
=81×9-4×2
=729-8
=721(cm3)
图形的体积是721cm3。
10.480cm3;343cm3
【分析】先统一单位,再根据长方体的体积=长×宽×高,正方体的体积=棱长×棱长×棱长,代入数据即可求出长方体和正方体的体积。
【详解】左图:1.2dm=12cm
12×5×8=480(cm3)
长方体的体积是480 cm3。
右图:7×7×7=343(cm3)
正方体的体积是343cm3。
11.256 cm2;240 cm3;238 cm2;199 cm3;250 cm2;171 cm3
【分析】根据长方体的表面积=(长×宽+长×高+宽×高)×2,长方体的体积=长×宽×高,正方体的表面积=棱长×棱长×6,正方体的体积=棱长×棱长×棱长;图1代入公式即可求解;图2体积等于正方体和长方体的体积之和,表面积等于正方体和长方体的表面积之和减去重叠部分的两个正方形的面积;图3体积等于两个长方体的体积之和,表面积等于两个长方体的表面积之和减去重叠部分的两个长方形的面积;据此解答即可。
【详解】图1:
表面积:(12×5+12×4+5×4)×2
=(60+48+20)×2
=(108+20)×2
=128×2
=256(cm2)
体积:12×5×4
=60×4
=240(cm3)
图2:
表面积:4×4×6+(9×5+9×3+5×3)×2-4×4×2
=16×6+(45+27+15)×2-16×2
=96+(72+15)×2-32
=96+87×2-32
=96+174-32
=270-32
=238(cm2)
体积:4×4×4+9×5×3
=16×4+45×3
=64+135
=199(cm3)
图3:
表面积:(7×3+7×1+3×1)×2+(15×5+15×2+5×2)×2-7×3×2
=(21+7+3)×2+(75+30+10)×2-21×2
=(28+3)×2+(105+10)×2-42
=31×2+115×2-42
=62+230-42
=292-42
=250(cm2)
体积:7×3×1+15×5×2
=21×1+75×2
=21+150
=171(cm3)
12.体积为875立方厘米;表面积为700平方厘米。
【分析】题干中图形是由一个棱长10厘米的正方体挖去一个棱长为5厘米的正方体得到,根据正方体体积=棱长×棱长×棱长,图形体积=大正方体体积 小正方体积可得出体积。
表面积增加了小正方体4个侧面的面积,根据边长×边长×4得出表面积。
【详解】图形体积为:
(立方厘米)
图形表面积为:
(平方厘米)
13.(1)表面积:57平方厘米;体积:27立方厘米
(2)表面积:244平方厘米;体积:219立方厘米
【分析】(1)根据长方体的表面积公式:S=(ab+ah+bh)×2,长方体的体积公式:V=abh,据此代入数值进行计算即可;
(2)观察图形可知,该图形的表面积等于下方长方体的表面积加上上方正方体的侧面积,根据长方体的表面积公式:S=(ab+ah+bh)×2,正方体的侧面积=棱长×棱长×4,据此代入数值进行计算即可;该图形的体积等于上方正方体的体积加上下方长方体的体积,根据正方体的体积公式:V=a3,长方体的体积公式:V=abh,据此进行计算即可。
【详解】(1)表面积:
(4.5×2+4.5×3+3×2)×2
=(9+13.5+6)×2
=28.5×2
=57(平方厘米)
体积:4.5×3×2
=13.5×2
=27(立方厘米)
图形的表面积是57平方厘米,体积是27立方厘米。
(2)表面积:
(8×4+8×6+6×4)×2+3×3×4
=(32+48+24)×2+3×3×4
=104×2+3×3×4
=208+36
=244(平方厘米)
体积:8×4×6+3×3×3
=192+27
=219(立方厘米)
图形的表面积是244平方厘米,体积是219立方厘米。
14.表面积: 42dm2
体积:14dm3
【分析】根据图可知:表面积相当于求一个大正方体的表面积外加长方体的前后两个面以及上下两个面的面积,根据正方体的表面积公式:棱长×棱长×6,以及长方形的面积公式:长×宽,把数代入即可求解;
根据长方体的体积公式:长×宽×高,正方体的体积公式:棱长×棱长×棱长,把数代入即可求出两部分的体积,再相加即可。
【详解】2×2×6+1×3×2+2×3×2
=24+6+12
=42(dm2)
2×2×2+1×3×2
=8+6
=14(dm3)
表面积是42dm2,体积是14dm3。
15.76cm3
【分析】根据长方体的体积公式:长×宽×高,分别求出两个长方体的体积,相加即可。
【详解】1×4×3
=4×3
=12(cm3)
8×4×2
=32×2
=64(cm3)
12+64=76(cm3)
则组合图形的体积是76cm3。
16.左图:190平方厘米;105立方厘米
右图:152平方厘米;84立方厘米
【分析】左图:该立体图形的表面积,就等于一个最大的长方体的表面积,该长方体长为10厘米,宽5厘米,高3厘米,根据长方体的表面积公式:S=(ab+ah+bh)×2,代入数据求表面积即可;该立体图形的体积,可以看作两个长方体的体积,一个是下面的扁一点的长方体,该长方体长为10厘米,宽为5厘米,高为1.5厘米,另外一个长方体是在上方的稍微小一点的长方体,该长方体长为10厘米,宽为2厘米,高为(3-1.5)厘米,根据长方体的体积公式:V=abh,代入数据求体积即可。
右图:该立体图形的表面积,就等于一个最大的长方体的表面积,该长方体长为8厘米,宽6厘米,高2厘米,根据长方体的表面积公式:S=(ab+ah+bh)×2,代入数据求表面积即可;该立方体的体积,可以看作大的长方体的体积减去一个小长方体体积,小长方体长为4厘米,宽为3厘米,高为1厘米,根据长方体的体积公式:V=abh,代入数据求体积即可。
【详解】由分析可得:
左面图形表面积:
(10×5+10×3+3×5)×2
=(50+30+15)×2
=(80+15)×2
=95×2
=190(平方厘米)
左面图形体积:
10×5×1.5+10×2×(3-1.5)
=50×1.5+10×2×1.5
=75+20×1.5
=75+30
=105(立方厘米)
右面图形表面积:
(8×6+8×2+2×6)×2
=(48+16+12)×2
=(64+12)×2
=76×2
=152(平方厘米)
右面图形体积:
8×6×2-4×3×1
=48×2-12×1
=96-12
=84(立方厘米)
17.表面积:260cm2;体积:219cm3
【分析】表面积=长是8cm,宽是8cm,高是3cm的长方体的表面积+棱长是3cm的侧面积;根据长方体表面积公式:表面积=(长×宽+长×高+宽×高)×2;正方体侧面积公式:棱长×棱长×4,代入数据,即可解答。
体积=长是8cm,宽是8cm,高是3cm的长方体的体积+棱长是3cm的正方体的体积;根据长方体的体积公式:体积=长×宽×高;正方体体积公式:体积=棱长×棱长×棱长,代入数据,即可解答。
【详解】表面积:(8×8+8×3+8×3)×2+3×3×4
=(64+24+24)×2+9×4
=(88+24)×2+36
=112×2+36
=224+36
=260(cm2)
体积:8×8×3+3×3×3
=64×3+9×3
=192+27
=219(cm3)
18.109立方厘米
【分析】观察题意可知,立体图形的体积=一个棱长为5厘米的正方体体积-一个长是4厘米、宽是2厘米、高是2厘米的长方体的体积,根据长方体的体积=长×宽×高,正方体的体积=棱长×棱长×棱长,代入数据解答。
【详解】5×5×5-4×2×2
=125-16
=109(立方厘米)
立体图形的体积是109立方厘米。
19.40cm3
【分析】根据图可知,这个组合体是一个长方体和一个正方体组成,根据长方体的体积公式:长×宽×高;正方体体积公式:棱长×棱长×棱长,把数代入公式即可求出两个部分的体积,再相加即可求解。
【详解】4×2×4+2×2×2
=32+8
=40(cm3)
这个组合体的体积是40cm3。
20.表面积:844 cm2;体积:1416cm3
【分析】观察图形可知:组合图形的表面积=正方体的侧面积+长方体的表面积,根据正方体的侧面积=棱长×棱长×4,长方体的表面积=(长×宽+长×高+宽×高)×2,代入数据计算即可解答;组合图形的体积等于正方体的体积加上长方体的体积,根据正方体的体积=棱长×棱长×棱长,长方体的体积=长×宽×高,代入数据解答即可。
【详解】表面积:(15×10+15×8+10×8)×2+6×6×4
=(150+120+80)×2+144
=350×2+144
=700+144
=844(cm2)
体积:15×10×8+6×6×6
=1200+216
=1416(cm3)
21.198cm2;135cm3
【分析】通过对图形的观察可知,正方体和长方体是粘在一起的,所以求组合体表面积的时候,上面正方体只求它的4个侧面的面积,下面长方体求整个的表面积,二者相加即可;组合体的体积等于正方体体积加上长方体体积,根据正方体的表面积公式:S=6a2,正方体体积公式:V=a3,长方体表面积公式:S=(ab+ah+bh)×2,长方体体积公式:V=abh,将图中数据代入公式求解即可。
【详解】正方体四个侧面面积为:
3×3×4
=9×4
=36(cm2)
长方体表面积为:
(12×3+12×3+3×3)×2
=(36+36+9)×2
=(72+9)×2
=81×2
=162(cm2)
组合体表面积为:
36+162=198(cm2)
正方体体积为:
3×3×3
=9×3
=27(cm3)
长方体体积为:
12×3×3
=36×3
=108(cm3)
组合体体积为:
27+108=135(cm3)
22.508平方厘米;700立方厘米
【分析】由图可知:将切去部分的底面平移到上面,切去部分的左面平移到右面,则立体图形的表面积=未切前大长方体的表面积-切去部分前后面面积和;立体图形的体积=未切前的体积-切去部分体积;根据长方形面积公式:S=ab,长方体表面积公式:S=(ab+ah+bh)×2,长方体体积公式:V=abh;据此代入数据解答。
【详解】表面积:(12×7+12×10+7×10)×2-4×5×2
=(84+120+70)×2-40
=274×2-40
=548-40
=508(平方厘米)
体积:12×7×10-4×7×5
=840-140
=700(立方厘米)
中小学教育资源及组卷应用平台
北师大版五年级下册数学第四单元长方体(二)图形计算题训练
1.计算下面各图形的体积。(单位:厘米)
2.计算下面立体图形的表面积和体积。(单位:cm)
3.计算下图中空心砖的体积。(单位:分米)
4.下图是长方体的展开图,求出这个长方体的表面积和体积。
5.计算下面立体图形的表面积和体积。
6.求下面各立体图形的体积。(单位:cm)
(1) (2)
7.计算下面各图形的表面积和体积。
(1) (2)
8.求下列图形的表面积和体积。(单位:dm)
9.求下图的体积。
10.求下面图形的体积。
11.计算下列图形的表面积和体积。(单位:cm)
12.计算下面图形的体积和表面积。(单位:厘米)
13.求出下面图形的表面积和体积。(单位:厘米)
(1)
(2)
14.计算下面立体图形的表面积和体积。(单位:dm)
15.算出下面组合图形的体积。
16.计算下面图形的表面积和体积。(单位:厘米)
17.求出下面图形的表面积和体积。
18.计算下图的体积。(单位:厘米)
19.计算体积。(单位:cm)
20.计算下面组合图形的表面积和体积。
21.计算下面图形的表面积和体积。
22.计算下面图形的表面积和体积。
《北师大版五年级下册数学第四单元长方体(二)图形计算题训练》参考答案
1.512立方厘米;1080立方厘米
【分析】由图一可知,正方体的棱长是8厘米,根据正方体的体积=棱长×棱长×棱长,将棱长代入公式即可求出正方体的体积;
由图二可知,长方体的长是15厘米,宽是8厘米,高是9厘米,长方体的体积=长×宽×高,将长、宽、高的数据代入公式计算即可解答。
【详解】正方体的体积:
8×8×8
=64×8
=512(立方厘米)
长方体的体积:
15×8×9
=120×9
=1080(立方厘米)
2.224cm2;208cm3
【分析】通过平移的知识可以发现,立体图形的表面积比棱长为6cm的正方体的表面积多了2个边长为2cm的正方形的面积,根据正方体的表面积=棱长×棱长×6,正方形的面积=边长×边长,代入数据计算即可;立体图形的体积=大正方体的体积-小正方体的体积,根据正方体的体积=棱长×棱长×棱长即可解答。
【详解】6×6×6+2×2×2
=36×6+4×2
=216+8
=224(cm2)
6×6×6-2×2×2
=36×6-4×2
=216-8
=208(cm3)
立体图形的表面积是224cm2,体积是208cm3。
3.27.5立方分米
【分析】根据长方体的体积=长×宽×高,分别求出外面大长方体的体积和内部挖掉的小长方体体积,再用减法求出差,即可得空心砖的体积。
【详解】4×2.5×3-1×1×2.5
=30-2.5
=27.5(立方分米)
这个空心砖的体积是27.5立方分米。
4.表面积:158平方分米;体积:120立方分米
【分析】观察图形可知,长方体的长是8分米,宽是5分米,高是3分米;根据长方体表面积=(长×宽+长×高+宽×高)×2,长方体体=长×宽×高,代入数据,即可解答。
【详解】长方体的长是8分米,宽是5分米,高是3分米。
表面积:(8×5+8×3+5×3)×2
=(40+24+15)×2
=(64+15)×2
=79×2
=158(平方分米)
体积:8×5×3
=40×3
=120(立方分米)
长方体的表面积是158平方分米,体积是120立方米。
5.152平方分米;88立方分米
【分析】由图可知:在大长方体的顶点处去掉一个小长方体,虽然体积减少了,但是表面积不变。根据长方体的表面积S=(ab+ah+bh)×2,求出立体图形的表面积。长方体的体积V=abh,用大长方体的体积减去小长方体的体积,求出立体图形的体积。
【详解】立体图形的表面积:
=(48+16+12)×2
=(64+12)×2
=76×2
=152(平方分米)
立体图形的体积:
=48×2-4×2×1
=96-8
=88(立方分米)
图形的表面积是152平方分米,体积是88立方分米。
6.(1)325cm3;(2)580cm3
【分析】(1)观察图形可知,组合图形的体积=正方体的体积+长方体的体积,根据正方体的体积公式V=a3,长方体的体积公式V=abh,代入数据计算求解。
(2)如下图,把组合图形分成左右两部分,那么组合图形的体积=大长方体的体积+小长方体的体积,根据长方体的体积公式V=abh,代入数据计算求解。
【详解】(1)5×5×5+8×5×5
=125+200
=325(cm3)
组合图形的体积是325cm3。
(2)8×10×(2+3)+6×10×3
=8×10×5+180
=400+180
=580(cm3)
组合图形的体积是580cm3。
7.(1)94cm2;60cm3
(2)1204cm2;2328cm3
【分析】(1)根据长方体的表面积公式S=2(ab+ah+bh),长方体的体积公式V=abh,代入数据计算求出长方体的表面积和体积。
(2)如下图,把长方体的右面如箭头所示向左平移,补给正方体的右面,这样正方体的表面积是6个面的面积之和,而长方体的表面积只需计算4个面(上下面和前后面)的面积。
因此组合图形的表面积=正方体的表面积+长方体上下面的面积+长方体前后面的面积;
根据正方体的表面积公式S=6a2,长方体4个面的面积之和公式S=2ab+2ah,代入数据计算求解。
组合图形的体积=正方体的体积+长方体的体积,根据正方体的体积公式V=a3,长方体的体积公式V=abh,代入数据计算求解。
【详解】(1)表面积:
(3×4+3×5+4×5)×2
=(12+15+20)×2
=47×2
=94(cm2)
体积:
3×4×5=60(cm3)
长方体的表面积是94cm2,体积是60cm3。
(2)表面积:
12×12×6+10×12×2+10×5×2
=864+240+100
=1204(cm2)
体积:
12×12×12+10×12×5
=1728+600
=2328(cm3)
组合图形的表面积是1204cm2,体积是2328cm3。
8.3.5dm2,0.375dm3;177dm2,154dm3
【分析】
如图,组合体的表面积=完整的长方体表面积+正方体一个面的面积×4,看图可知,长方体是有2个面是正方形的特殊长方体,前后左右4个面的面积相等,这个长方体表面积=长×宽×2+长×高×4,组合体的体积=长方体体积+正方体体积,长方体体积=长×宽×高,正方体体积=棱长×棱长×棱长;
长方体表面积=(长×宽+长×高+宽×高)×2,长方体体积=长×宽×高,据此列式计算。
【详解】1-0.5=0.5(dm)
0.5×0.5×2+0.5×1×4+0.5×0.5×4
=0.5+2+1
=3.5(dm2)
0.5×0.5×1+0.5×0.5×0.5
=0.25+0.125
=0.375(dm3)
(4×7+4×5.5+7×5.5)×2
=(28+22+38.5)×2
=88.5×2
=177(dm2)
4×7×5.5=154(dm3)
组合体的表面积是3.5dm2,体积是0.375dm3;长方体的表面积是177dm2,体积是154dm3。
9.721cm3
【分析】观察图形可知,图形的体积=大正方体的体积-小正方体的体积,根据正方体的体积公式V=a3,代入数据计算求解。
【详解】9×9×9-2×2×2
=81×9-4×2
=729-8
=721(cm3)
图形的体积是721cm3。
10.480cm3;343cm3
【分析】先统一单位,再根据长方体的体积=长×宽×高,正方体的体积=棱长×棱长×棱长,代入数据即可求出长方体和正方体的体积。
【详解】左图:1.2dm=12cm
12×5×8=480(cm3)
长方体的体积是480 cm3。
右图:7×7×7=343(cm3)
正方体的体积是343cm3。
11.256 cm2;240 cm3;238 cm2;199 cm3;250 cm2;171 cm3
【分析】根据长方体的表面积=(长×宽+长×高+宽×高)×2,长方体的体积=长×宽×高,正方体的表面积=棱长×棱长×6,正方体的体积=棱长×棱长×棱长;图1代入公式即可求解;图2体积等于正方体和长方体的体积之和,表面积等于正方体和长方体的表面积之和减去重叠部分的两个正方形的面积;图3体积等于两个长方体的体积之和,表面积等于两个长方体的表面积之和减去重叠部分的两个长方形的面积;据此解答即可。
【详解】图1:
表面积:(12×5+12×4+5×4)×2
=(60+48+20)×2
=(108+20)×2
=128×2
=256(cm2)
体积:12×5×4
=60×4
=240(cm3)
图2:
表面积:4×4×6+(9×5+9×3+5×3)×2-4×4×2
=16×6+(45+27+15)×2-16×2
=96+(72+15)×2-32
=96+87×2-32
=96+174-32
=270-32
=238(cm2)
体积:4×4×4+9×5×3
=16×4+45×3
=64+135
=199(cm3)
图3:
表面积:(7×3+7×1+3×1)×2+(15×5+15×2+5×2)×2-7×3×2
=(21+7+3)×2+(75+30+10)×2-21×2
=(28+3)×2+(105+10)×2-42
=31×2+115×2-42
=62+230-42
=292-42
=250(cm2)
体积:7×3×1+15×5×2
=21×1+75×2
=21+150
=171(cm3)
12.体积为875立方厘米;表面积为700平方厘米。
【分析】题干中图形是由一个棱长10厘米的正方体挖去一个棱长为5厘米的正方体得到,根据正方体体积=棱长×棱长×棱长,图形体积=大正方体体积 小正方体积可得出体积。
表面积增加了小正方体4个侧面的面积,根据边长×边长×4得出表面积。
【详解】图形体积为:
(立方厘米)
图形表面积为:
(平方厘米)
13.(1)表面积:57平方厘米;体积:27立方厘米
(2)表面积:244平方厘米;体积:219立方厘米
【分析】(1)根据长方体的表面积公式:S=(ab+ah+bh)×2,长方体的体积公式:V=abh,据此代入数值进行计算即可;
(2)观察图形可知,该图形的表面积等于下方长方体的表面积加上上方正方体的侧面积,根据长方体的表面积公式:S=(ab+ah+bh)×2,正方体的侧面积=棱长×棱长×4,据此代入数值进行计算即可;该图形的体积等于上方正方体的体积加上下方长方体的体积,根据正方体的体积公式:V=a3,长方体的体积公式:V=abh,据此进行计算即可。
【详解】(1)表面积:
(4.5×2+4.5×3+3×2)×2
=(9+13.5+6)×2
=28.5×2
=57(平方厘米)
体积:4.5×3×2
=13.5×2
=27(立方厘米)
图形的表面积是57平方厘米,体积是27立方厘米。
(2)表面积:
(8×4+8×6+6×4)×2+3×3×4
=(32+48+24)×2+3×3×4
=104×2+3×3×4
=208+36
=244(平方厘米)
体积:8×4×6+3×3×3
=192+27
=219(立方厘米)
图形的表面积是244平方厘米,体积是219立方厘米。
14.表面积: 42dm2
体积:14dm3
【分析】根据图可知:表面积相当于求一个大正方体的表面积外加长方体的前后两个面以及上下两个面的面积,根据正方体的表面积公式:棱长×棱长×6,以及长方形的面积公式:长×宽,把数代入即可求解;
根据长方体的体积公式:长×宽×高,正方体的体积公式:棱长×棱长×棱长,把数代入即可求出两部分的体积,再相加即可。
【详解】2×2×6+1×3×2+2×3×2
=24+6+12
=42(dm2)
2×2×2+1×3×2
=8+6
=14(dm3)
表面积是42dm2,体积是14dm3。
15.76cm3
【分析】根据长方体的体积公式:长×宽×高,分别求出两个长方体的体积,相加即可。
【详解】1×4×3
=4×3
=12(cm3)
8×4×2
=32×2
=64(cm3)
12+64=76(cm3)
则组合图形的体积是76cm3。
16.左图:190平方厘米;105立方厘米
右图:152平方厘米;84立方厘米
【分析】左图:该立体图形的表面积,就等于一个最大的长方体的表面积,该长方体长为10厘米,宽5厘米,高3厘米,根据长方体的表面积公式:S=(ab+ah+bh)×2,代入数据求表面积即可;该立体图形的体积,可以看作两个长方体的体积,一个是下面的扁一点的长方体,该长方体长为10厘米,宽为5厘米,高为1.5厘米,另外一个长方体是在上方的稍微小一点的长方体,该长方体长为10厘米,宽为2厘米,高为(3-1.5)厘米,根据长方体的体积公式:V=abh,代入数据求体积即可。
右图:该立体图形的表面积,就等于一个最大的长方体的表面积,该长方体长为8厘米,宽6厘米,高2厘米,根据长方体的表面积公式:S=(ab+ah+bh)×2,代入数据求表面积即可;该立方体的体积,可以看作大的长方体的体积减去一个小长方体体积,小长方体长为4厘米,宽为3厘米,高为1厘米,根据长方体的体积公式:V=abh,代入数据求体积即可。
【详解】由分析可得:
左面图形表面积:
(10×5+10×3+3×5)×2
=(50+30+15)×2
=(80+15)×2
=95×2
=190(平方厘米)
左面图形体积:
10×5×1.5+10×2×(3-1.5)
=50×1.5+10×2×1.5
=75+20×1.5
=75+30
=105(立方厘米)
右面图形表面积:
(8×6+8×2+2×6)×2
=(48+16+12)×2
=(64+12)×2
=76×2
=152(平方厘米)
右面图形体积:
8×6×2-4×3×1
=48×2-12×1
=96-12
=84(立方厘米)
17.表面积:260cm2;体积:219cm3
【分析】表面积=长是8cm,宽是8cm,高是3cm的长方体的表面积+棱长是3cm的侧面积;根据长方体表面积公式:表面积=(长×宽+长×高+宽×高)×2;正方体侧面积公式:棱长×棱长×4,代入数据,即可解答。
体积=长是8cm,宽是8cm,高是3cm的长方体的体积+棱长是3cm的正方体的体积;根据长方体的体积公式:体积=长×宽×高;正方体体积公式:体积=棱长×棱长×棱长,代入数据,即可解答。
【详解】表面积:(8×8+8×3+8×3)×2+3×3×4
=(64+24+24)×2+9×4
=(88+24)×2+36
=112×2+36
=224+36
=260(cm2)
体积:8×8×3+3×3×3
=64×3+9×3
=192+27
=219(cm3)
18.109立方厘米
【分析】观察题意可知,立体图形的体积=一个棱长为5厘米的正方体体积-一个长是4厘米、宽是2厘米、高是2厘米的长方体的体积,根据长方体的体积=长×宽×高,正方体的体积=棱长×棱长×棱长,代入数据解答。
【详解】5×5×5-4×2×2
=125-16
=109(立方厘米)
立体图形的体积是109立方厘米。
19.40cm3
【分析】根据图可知,这个组合体是一个长方体和一个正方体组成,根据长方体的体积公式:长×宽×高;正方体体积公式:棱长×棱长×棱长,把数代入公式即可求出两个部分的体积,再相加即可求解。
【详解】4×2×4+2×2×2
=32+8
=40(cm3)
这个组合体的体积是40cm3。
20.表面积:844 cm2;体积:1416cm3
【分析】观察图形可知:组合图形的表面积=正方体的侧面积+长方体的表面积,根据正方体的侧面积=棱长×棱长×4,长方体的表面积=(长×宽+长×高+宽×高)×2,代入数据计算即可解答;组合图形的体积等于正方体的体积加上长方体的体积,根据正方体的体积=棱长×棱长×棱长,长方体的体积=长×宽×高,代入数据解答即可。
【详解】表面积:(15×10+15×8+10×8)×2+6×6×4
=(150+120+80)×2+144
=350×2+144
=700+144
=844(cm2)
体积:15×10×8+6×6×6
=1200+216
=1416(cm3)
21.198cm2;135cm3
【分析】通过对图形的观察可知,正方体和长方体是粘在一起的,所以求组合体表面积的时候,上面正方体只求它的4个侧面的面积,下面长方体求整个的表面积,二者相加即可;组合体的体积等于正方体体积加上长方体体积,根据正方体的表面积公式:S=6a2,正方体体积公式:V=a3,长方体表面积公式:S=(ab+ah+bh)×2,长方体体积公式:V=abh,将图中数据代入公式求解即可。
【详解】正方体四个侧面面积为:
3×3×4
=9×4
=36(cm2)
长方体表面积为:
(12×3+12×3+3×3)×2
=(36+36+9)×2
=(72+9)×2
=81×2
=162(cm2)
组合体表面积为:
36+162=198(cm2)
正方体体积为:
3×3×3
=9×3
=27(cm3)
长方体体积为:
12×3×3
=36×3
=108(cm3)
组合体体积为:
27+108=135(cm3)
22.508平方厘米;700立方厘米
【分析】由图可知:将切去部分的底面平移到上面,切去部分的左面平移到右面,则立体图形的表面积=未切前大长方体的表面积-切去部分前后面面积和;立体图形的体积=未切前的体积-切去部分体积;根据长方形面积公式:S=ab,长方体表面积公式:S=(ab+ah+bh)×2,长方体体积公式:V=abh;据此代入数据解答。
【详解】表面积:(12×7+12×10+7×10)×2-4×5×2
=(84+120+70)×2-40
=274×2-40
=548-40
=508(平方厘米)
体积:12×7×10-4×7×5
=840-140
=700(立方厘米)
