北师大版五年级下册数学第四单元长方体(二)应用题训练(含解析)
文档属性
| 名称 | 北师大版五年级下册数学第四单元长方体(二)应用题训练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 428.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 08:08:30 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
北师大版五年级下册数学第四单元长方体(二)应用题训练
1.深圳大运中心游泳馆比赛池的长是50米、宽是25米、深是2米。往池里加水至1.8米深,按5元/立方米计算,这池水的水费是多少元?
2.工人叔叔要把一个棱长6厘米的正方体钢坯锻造成一个长9厘米、宽6厘米的长方体零件,这个零件的高是多少厘米?
3.一个正方体油箱,棱长4分米,装满油后倒入一个长8分米、宽2分米的长方体油箱中,油深多少分米?
4.一个长方体的底面是一个周长为30厘米的长方形,高是10厘米,如果它的长宽都是合数,那么这个长方体的体积是多少立方厘米?
5.一个长方体容器,底面长2分米、宽1.5分米,放入一个土豆后水面升高了0.2分米,这个土豆的体积是多少?
6.淘气和笑笑各有一瓶同样多的饮料,淘气倒了3杯,而笑笑只倒了2杯,你认为有可能吗?说一说你的想法。
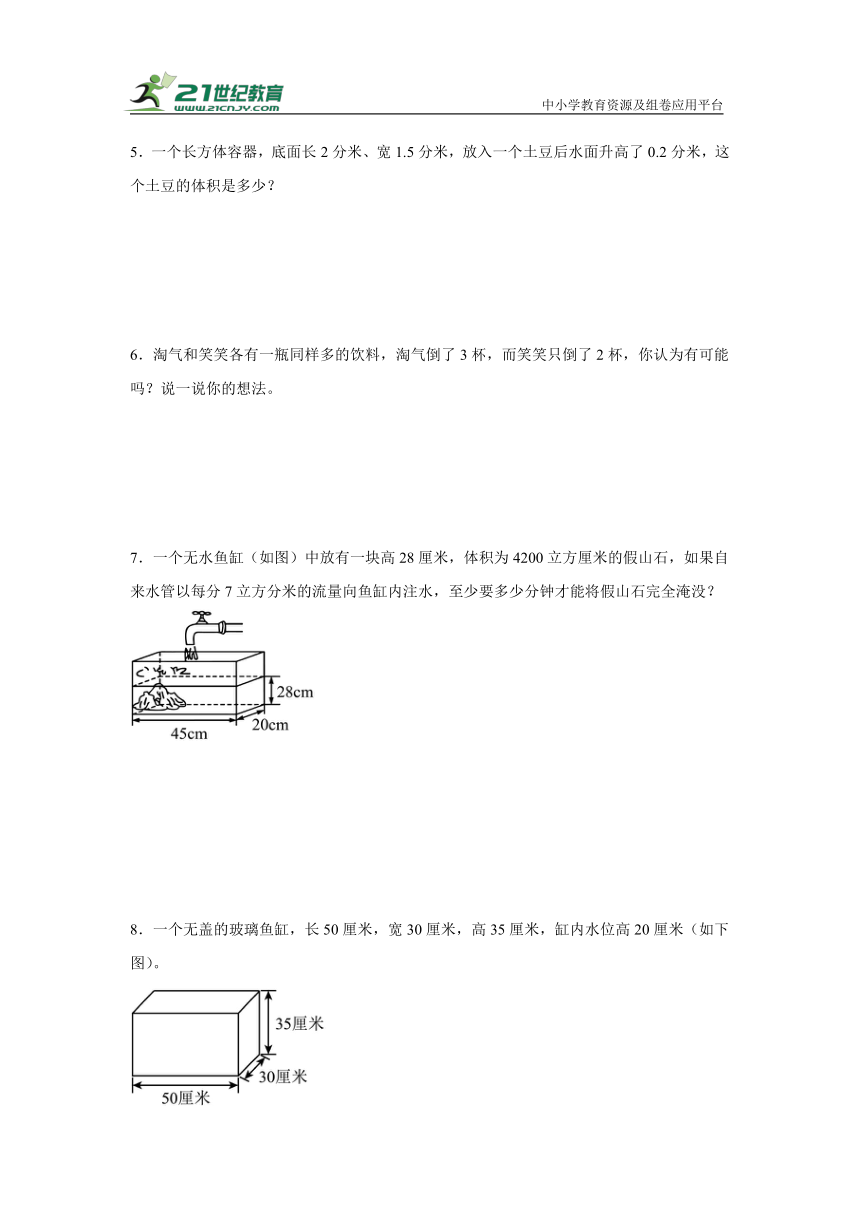
7.一个无水鱼缸(如图)中放有一块高28厘米,体积为4200立方厘米的假山石,如果自来水管以每分7立方分米的流量向鱼缸内注水,至少要多少分钟才能将假山石完全淹没?
8.一个无盖的玻璃鱼缸,长50厘米,宽30厘米,高35厘米,缸内水位高20厘米(如下图)。
(1)制作这个鱼缸至少需要多少平方厘米的玻璃?
(2)如果向这个鱼缸倒入3000毫升水和一些细沙,这时水面上升到30厘米,倒入了多少立方厘米的细沙(玻璃厚度忽略不计)?
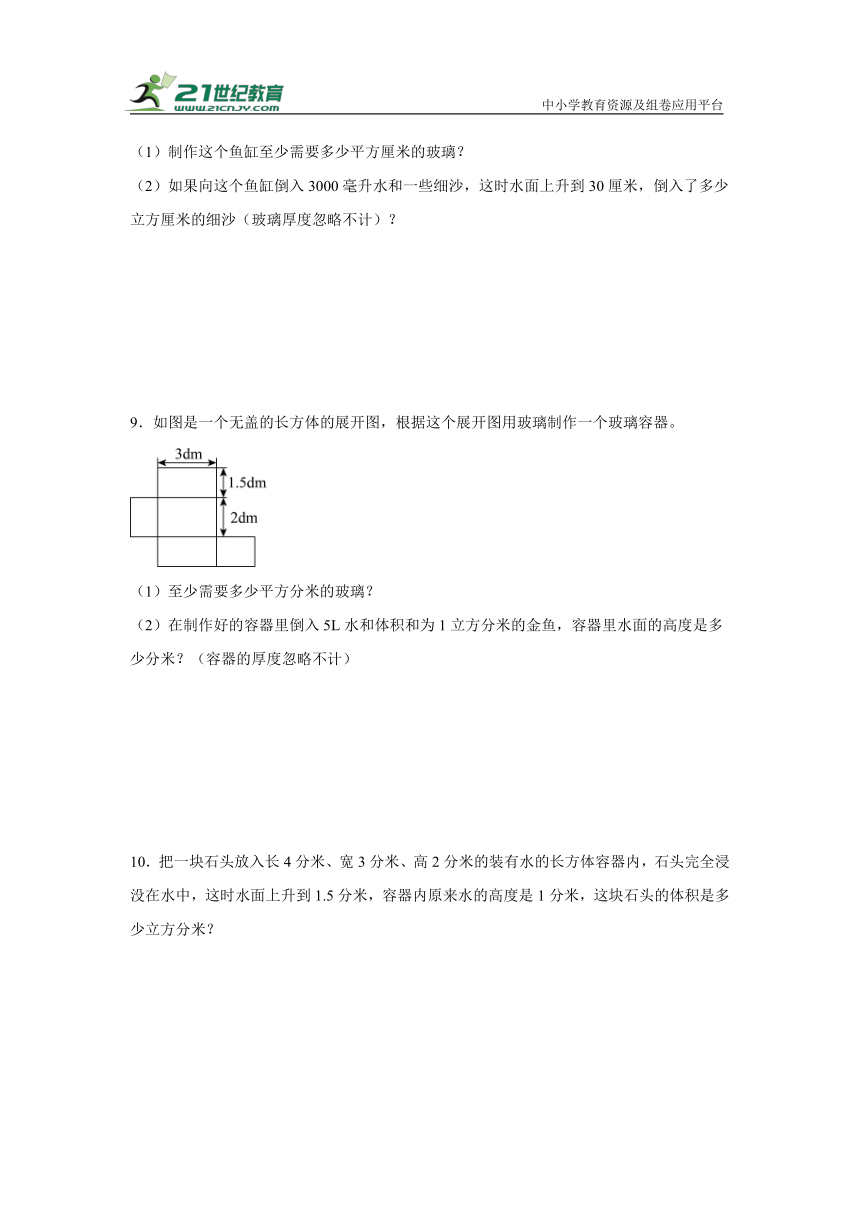
9.如图是一个无盖的长方体的展开图,根据这个展开图用玻璃制作一个玻璃容器。
(1)至少需要多少平方分米的玻璃?
(2)在制作好的容器里倒入5L水和体积和为1立方分米的金鱼,容器里水面的高度是多少分米?(容器的厚度忽略不计)
10.把一块石头放入长4分米、宽3分米、高2分米的装有水的长方体容器内,石头完全浸没在水中,这时水面上升到1.5分米,容器内原来水的高度是1分米,这块石头的体积是多少立方分米?
11.学校修建了一个长50米,宽20米,高1.8米的游泳池。
(1)在池底和四周贴上瓷砖,贴瓷砖的面积是多少平方米?
(2)游泳池中共注水1500立方米,水面距池口多少米?
12.游泳馆新建一个游泳池,长30米、宽20米、深2米。游泳池的四壁和底面铺瓷砖。
(1)需要铺瓷砖的面积是多少平方米?
(2)如果给游泳池注水960立方米,游泳池水深多少米?
13.一个长方体水箱,从里面量得长是30厘米,宽是15厘米。水箱中完全浸没一块石头后,水深20厘米。当取出这块石头后,水深16厘米。这块石头的体积是多少立方分米?
14.下面是一个长方体盒子的展开图。(单位:厘米)
(1)长方体盒子的表面积是多少平方厘米?
(2)长方体盒子的体积是多少立方厘米?
15.仔细观察下图,石块的体积是多少立方厘米?(容器底面是正方形)
16.一个长方体果汁盒从里面量长9厘米,宽6厘米,高19厘米,包装盒上标着“净含量1升”的字样,这个果汁盒能不能装进1升的果汁呢?
17.如图,将一根长48分米的长方体木料截成两段,表面积比原来增加了45平方分米,原来这根木料的体积是多少立方米?
18.一个正方体容器,从里面量,棱长是50厘米,其中水深30厘米。另有一个长、宽、高分别为35厘米、20厘米、20厘米的长方体铁块。把铁块横着放入水中,被完全淹没,此时水位将升高多少分米?
19.如图是一个无盖的长方体玻璃容器。
(1)这个长方体玻璃容器的表面积是多少平方厘米?
(2)如果放进一个铁块并完全浸没在水中(如图所示),1立方厘米的铁块重7.9克,这个铁块有多少克?
20.体育馆计划建一个长10米、宽6米、高25分米的游泳池,请你帮助设计:
(1)它的占地面积是多少平方米?
(2)把它的四周和底面铺上方砖,铺方砖的面积是多少?
(3)建造这个游泳池能挖出多少方土?
21.一个无水的观赏鱼缸中放着一块高为3分米、体积为4立方分米的假山石(如图)。现在需要向鱼缸中注水完全淹没假山石。
(1)至少需要多少升水?
(2)如果取出假山石,水面会下降多少厘米?
22.将如图中的铁皮折弯后焊接成一个无盖的长方体铁桶,这个铁桶最多可以装多少升水?(铁皮厚度不计)
23.健身中心新建的游泳池长50米,宽25米,深2.2米。
(1)这个游泳池最多可蓄水多少立方米?
(2)要在它的四壁和底部铺上瓷砖,铺瓷砖部分的面积是多少平方米?
24.张叔叔要制作一个棱长为15厘米的正方体无盖玻璃鱼缸。
(1)至少需要玻璃多少平方厘米?
(2)这个鱼缸最多可装水多少升?(玻璃的厚度忽略不计)
25.张叔叔用铁皮做了一个长40厘米,宽20厘米,高52厘米的无盖长方体容器(甲),然后给这个容器中倒入高30厘米的水。
(1)张叔叔做这个长方体容器,至少需要铁皮多少平方厘米?(接头处不计)
(2)如果张叔叔将这个容器里的水全部倒入乙容器,乙容器的水面高多少厘米?
26.AI智能模块化鱼缸是一款科技感十足的智能鱼缸,它拥有自动定时喂食、自动清洁等多种功能,让养鱼这件事变得更加简单。张大爷家的智能鱼缸是长60厘米,宽和高都是40厘米的长方体。
(1)鱼缸的四周是钢化玻璃,为了防止玻璃自爆,需要在玻璃上贴一层防爆膜,一共需要贴多少平方米的防爆膜?(损耗忽略不计)
(2)鱼缸中放有一块高为24厘米,体积为1100立方厘米的假山石(如图),如果向鱼缸内注水,那么至少需要注入多少立方分米的水才能将假山石完全淹没?
27.笑笑家有一个收纳盒(如图1),她想把家里散落的小包纸巾(如图2)分别放入收纳盒中(纸巾不能超过收纳盒的上沿且不能挤压)。这个收纳盒中最多可以放置多少包纸巾?(单位:厘米)
28.先认真阅读下面的材料,并从中选择恰当的数学信息解决问题。
光明小学里有个快乐书吧,书吧室内量长10米、宽5.8米、高4米,门窗面积共6.3平方米。书吧服务台旁有一个长8分米、宽7分米、高5分米的长方体鱼缸。今年6月,书吧进行了重新装修:房间的四壁和房顶贴上了新的墙纸,地面重新铺了正方形的地砖,鱼缸(无盖)的棱上贴上了装饰条,鱼缸里还放了美丽的珊瑚石……
(1)装修时至少用了多少平方米的墙纸?
(2)鱼缸里原来水深3分米,放入珊瑚石(完全浸没)后,水面上升到4.5分米,珊瑚石的体积是多少立方分米?(鱼缸的厚度忽略不计)
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
《北师大版五年级下册数学第四单元长方体(二)应用题训练》参考答案
1.11250元
【分析】已知游泳馆比赛池的长、宽和注水的深度,根据长方体的体积公式:V=abh,把数据代入公式,求出注入水的体积;
然后根据单价×数量=总价,用每立方米水的价钱乘水的体积,即可求出这池水的水费。
【详解】50×25×1.8
=1250×1.8
=2250(立方米)
5×2250=11250(元)
答:这池水的水费是11250元。
2.4厘米
【分析】由题意可知,正方体钢坯锻造成长方体零件后体积不变,先根据“正方体的体积=棱长×棱长×棱长”求出钢坯的体积,再根据“长方体的高=长方体的体积÷长÷宽”求出这个零件的高度,据此解答。
【详解】6×6×6÷9÷6
=216÷9÷6
=24÷6
=4(厘米)
答:这个零件的高是4厘米。
3.4分米
【分析】先根据“正方体的体积=棱长×棱长×棱长”求出油的体积,长方体油箱中油的体积和正方体油箱中油的体积相等,长方体油箱中油的深度=油的体积÷长方体油箱的长÷长方体油箱的宽,据此解答。
【详解】4×4×4÷8÷2
=16×4÷8÷2
=64÷8÷2
=8÷2
=4(分米)
答:油深4分米。
4.540立方厘米
【分析】根据长方体周长=(长+宽)×2,可确定长与宽的和是15厘米,15以内的合数是:4、6、8、9、10、12、14、15,则长、宽是9厘米和6厘米。再根据长方体体积=长×宽×高,列式解答即可。
【详解】30÷2=15(厘米)
6和9都是合数且15=9+6,所以长、宽是9厘米、6厘米。
9×6×10
=54×10
=540(立方厘米)
答:这个长方体的体积是540立方厘米。
5.0.6立方分米
【分析】由题意可知,这个土豆的体积等于上升部分水的体积,上升部分水的体积=容器的长×容器的宽×上升部分水的高度,据此解答。
【详解】2×1.5×0.2
=3×0.2
=0.6(立方分米)
答:这个土豆的体积是0.6立方分米。
6.有可能;见详解
【分析】从题意可知:各有一瓶同样多的饮料,说明饮料的体积相同。倒的杯数不同,说明杯子的大小不同,即杯子的容积不同。杯子的容积大,倒的杯数少;杯子的容积小,倒的杯数多。据此解答。
【详解】答:我认为有可能,因为淘气杯子的容积小,倒的杯数多;笑笑杯子的容积大,倒的杯数少。
7.7分钟
【分析】假山石高28厘米,只有水面高度达到28厘米,才能将假山石完全淹没。根据长方体的体积=长×宽×高,求出长45厘米,宽20厘米,高28厘米的长方体的体积(水与假山石的体积之和),再减去假山石的体积,就得注水的体积。根据1立方分米=1000立方厘米,将水的体积换算成立方分米。最后根据每分注水7立方分米,用水的体积除以7即可求出注水时间。
【详解】45×20×28-4200
=25200-4200
=21000(立方厘米)
21000立方厘米=21立方分米
21÷7=3(分钟)
答:至少要7分钟才能将假山石完全淹没。
8.(1)7100平方厘米
(2)12000立方厘米
【分析】(1)这个无盖的玻璃鱼缸有下面和前后左右面积,玻璃的面积=长×宽+长×高×2+宽×高×2,代入数据计算即可,求出需要玻璃的面积。
(2)3000毫升=3000立方厘米。水面从20厘米上升到30厘米,上升了30-20=10厘米,这高10厘米的长方体的体积就是倒入的水和细沙的体积之和。根据长方体的体积(容积)=长×宽×高,代入数据计算,求出体积之和,再减去水的体积,就是沙子的体积。
【详解】(1)50×30+50×35×2+30×35×2
=1500+3500+2100
=7100(平方厘米)
答:制作这个鱼缸至少需要7100平方厘米的玻璃。
(2)3000毫升=3000立方厘米
50×30×(30-20)-3000
=50×30×10-3000
=15000-3000
=12000(立方厘米)
答:倒入了12000立方厘米的细沙。
9.(1)21平方分米
(2)1分米
【分析】(1)由展开图可知,这个长方体的长是3分米。宽是2分米,高是1.5分米,因为是无盖的,所以是求这个长方体5个面的面积和,根据无盖长方体的表面积=长×宽+(长×高+宽×高)×2,把数据代入公式即可求解;
(2)在制作好的容器里倒入5L水和体积和为1立方分米的金鱼,其总体积为5L水的体积和金鱼的体积和,根据长方体的体积公式:V=abh,那么h=V÷ab,把数据代入公式即可解答。
【详解】(1)(3×1.5+2×1.5)×2+3×2
=(4.5+3)×2+3×2
=7.5×2+3×2
=15+6
=21(平方分米)
答:至少需要21平方分米的玻璃。
(2)5L=5立方分米
(5+1)÷(3×2)
=6÷6
=1(分米)
答:容器里水面的高度是1分米。
10.6立方分米
【分析】根据题意,把一块石头完全浸没在水中,这时水面上升到1.5分米,则水面上升了(1.5-1)分米,那么水上升部分的体积就是这块石头的体积,根据长方体的体积公式V=abh,求出这块石头的体积。
【详解】4×3×(1.5-1)
=12×0.5
=6(立方分米)
答:这块石头的体积是6立方分米。
11.(1)1252平方米
(2)0.3米
【分析】(1)根据题意,求贴瓷砖的面积就是求长方体游泳池前后面、左右面和下面共5个面的总面积,根据前后面的面积=长×高×2,左右面的面积=宽×高×2,下面的面积=长×宽,可得:贴瓷砖的面积=长×高×2+宽×高×2+长×宽,据此解答。
(2)游泳池中共注水1500立方米,即水的体积是1500立方米,游泳池中的水呈长方体,长是50米,宽是20米,根据长×宽×高=长方体的体积可知:长方体的体积÷长÷宽=高,即可求到水的高度,再用游泳池的高度减水的高度,即得到水面距池口的米数。据此解答。
【详解】(1)50×1.8×2+20×1.8×2+50×20
=90×2+36×2+1000
=180+72+1000
=252+1000
=1252(平方米)
答:贴瓷砖的面积是1252平方米。
(2)1500÷50÷20
=30÷20
=1.5(米)
1.8-1.5=0.3(米)
答:水面距池口0.3米。
12.(1)800平方米
(2)1.6米
【分析】(1)求铺瓷砖的面积相当于求长方体前后左右和下面5个面的面积和,深相当于长方体的高,铺瓷砖的面积=长×宽+长×深×2+宽×深×2,据此列式解答。
(2)根据长方体的高=体积÷底面积=体积÷(长×宽),列式解答即可。
【详解】(1)30×20+30×2×2+20×2×2
=600+120+80
=800(平方米)
答:需要铺瓷砖的面积是800平方米。
(2)960÷(30×20)
=960÷600
=1.6(米)
答:游泳池水深1.6米。
13.1.8立方分米
【分析】根据题意,石头的体积=下降的水的体积。下降的水的形状是长30厘米,宽15厘米,高(20-16)厘米的长方体,根据长方体的体积=长×宽×高,代入数据计算即可。最后换算成以立方分米为单位的数。
【详解】30×15×(20-16)
=30×15×4
=1800(立方厘米)
=1.8(立方分米)
答:这块石头的体积是1.8立方分米。
14.(1)148平方厘米
(2)120立方厘米
【分析】(1)观察长方体盒子的展开图,可以确定长方体的长6厘米,宽5厘米,高4厘米,根据长方体表面积=(长×宽+长×高+宽×高)×2,列式解答即可;
(2)根据长方体体积=长×宽×高,列式解答。
【详解】(1)表面积:
(平方厘米)
答:长方体盒子的表面积是148平方厘米。
(2)体积:(立方厘米)
答:长方体盒子的体积是120立方厘米。
15.200立方厘米
【分析】看图可知,浸入石块水面上升了(8-6)厘米,水面上升的体积就是石块的体积,根据长方体体积公式,容器底面积×水面上升的高度=石块的体积,据此列式解答。
【详解】
(立方厘米)
答:石块的体积是200立方厘米。
16.能
【分析】根据长方体容积公式:容积=长×宽×高,代入数据,求出长方体果汁盒的容积,在换算成升,再和1升的果汁进行比较,即可解答。
【详解】9×6×19
=54×19
=1026(立方厘米)
1026立方厘米=1.026升
1.026升>1升,这个果汁盒能装进1升果汁。
答:这个果汁盒能装进1升的果汁。
17.1.08立方米
【分析】这根长方体木料截成两段后,表面积比原来增加了2个长方形的面积。已知表面积比原来增加了45平方分米,用45除以2即可求出一个长方形的面积,即横截面的面积。长方体的体积=横截面的面积×长,据此代入数据计算即可。
【详解】45÷2×48
=22.5×48
=1080(立方分米)
1080立方分米=1.08立方米
答:原来这根木料的体积是1.08立方米。
18.0.56分米
【分析】水位上升部分的体积等于放入长方体的体积,利用长方体体积公式:V=abh计算铁块的体积,再除以正方体容器的底面积即可求水位上升的高度。
【详解】35×20×20÷(50×50)
=700×20÷2500
=14000÷2500
=5.6(厘米)
5.6厘米=0.56分米
答:此时水位将升高0.56分米。
19.(1)410平方厘米
(2)790克
【分析】(1)求无盖长方体玻璃容器的表面积,就是求长方体的下面、前后面、左右面共5个面的面积之和;根据“长×宽+长×高×2+宽×高×2”,代入数据计算求解。
(2)从图中可知,长方体玻璃容器中放入一个铁块后,水面上升了(8-6)厘米,那么水上升部分的体积等于铁块的体积;根据长方体的体积公式V=abh,求出这个铁块的体积,再乘每立方厘米铁块的重量,即是这个铁块的总重量。
【详解】(1)10×5+10×12×2+5×12×2
=50+240+120
=410(平方厘米)
答:这个长方体玻璃容器的表面积是410平方厘米。
(2)10×5×(8-6)
=10×5×2
=100(立方厘米)
100×7.9=790(克)
答:这个铁块有790克。
20.(1)60平方米
(2)140平方米
(3)150方
【分析】(1)占地面积指的是底面积,占地面积=长×宽,据此列式解答;
(2)铺方砖的面积=底面积+长×高×2+宽×高×2,据此列式解答,注意统一单位;
(3)根据长方体体积=长×宽×高,即可求出挖出的土的体积,1方=1立方米。
【详解】(1)10×6=60(平方米)
答:它的占地面积是60平方米。
(2)25分米=2.5米
60+10×2.5×2+6×2.5×2
=60+50+30
=140(平方米)
答:铺方砖的面积是140平方米。
(3)10×6×2.5=150(立方米)=150(方)
答:建造这个游泳池能挖出150方土。
21.(1)92升
(2)1.25厘米
【分析】(1)当水完全淹没假山石时,水的体积和假山石的体积恰好为长8分米、宽4分米、高3分米的长方体的体积。要计算至少需要多少升水,先根据:长方体的体积=长×宽×高,算出鱼缸的体积,再减去假山石的体积。
(2)取出假山石后水面下降的高度可以通过假山石的体积除以鱼缸的底面积来计算。
【详解】(1)8×4×3-4
=96-4
=92(立方分米)
92立方分米=92升
答:至少需要92升的水。
(2)4÷(8×4)
=4÷32
=0.125(分米)
0.125分米=1.25厘米
答:如果取出假山石,水面会下降1.25厘米。
22.32升
【分析】通过观察图形可知,这个无盖长方体的底面是正方形,底面周长是80厘米,根据正方形的周长公式可以求出底面边长,底面边长加上高是100厘米,据此可以求出高,然后根据长方体的容积公式:V=abh,把数据代入公式解答。
【详解】底面边长:80÷4=20(厘米)
高:100-20=80(厘米)
20×20×80
=400×80
=32000(立方厘米)
32000立方厘米=32升
答:这条铁桶最多可以装32升水。
23.(1)2750立方米
(2)1580平方米
【分析】(1)根据长方体的容积公式:V=abh,代入数值进行计算即可;
(2)由题意可知,铺瓷砖部分的面积等于长方体五个面的面积,再结合长方体的五个面的面积=(长×高+宽×高)×2+长×宽,据此进行计算即可。
【详解】(1)50×25×2.2
=1250×2.2
=2750(立方米)
答:这个游泳池最多可蓄水2750立方米。
(2)(50×2.2+25×2.2)×2+50×25
=(110+55)×2+1250
=165×2+1250
=330+1250
=1580(平方米)
答:铺瓷砖部分的面积是1580平方米。
24.(1)1125平方厘米
(2)3.375升
【分析】(1)根据题意,要制作一个棱长为15厘米的正方体无盖玻璃鱼缸,求至少需要玻璃的面积,就是求正方体5个面的面积之和,根据“棱长×棱长×5”,代入数据计算求解。
(2)求这个鱼缸最多可装水的体积,就是求正方体的容积;根据正方体的体积(容积)公式V=a3,代入数据计算求解。注意单位的换算:1升=1000立方厘米。
【详解】(1)15×15×5
=225×5
=1125(平方厘米)
答:至少需要玻璃1125平方厘米。
(2)15×15×15
=225×15
=3375(立方厘米)
3375立方厘米=3.375升
答:这个鱼缸最多可装水3.375升。
25.(1)7040平方厘米
(2)16厘米
【分析】(1)无盖的长方体的表面积=长×宽+(长×高+宽×高)×2,据此代入数据计算即可解答;
(2)根据长方体的体积=长×宽×高计算出甲容器中水的体积,再用水的体积除以乙容器的底面积即可求出乙容器的水面高多少厘米。
【详解】(1)2×(40×52+20×52)+40×20
=2×(2080+1040)+40×20
=2×3120+40×20
=6240+800
=7040(平方厘米)
答:至少需要铁皮7040平方厘米。
(2)40×20×30
=800×30
=24000(立方厘米)
24000÷(60×25)
=24000÷1500
=16(厘米)
答:乙容器的水面高16厘米。
26.(1)0.8平方米
(2)56.5立方分米
【分析】(1)求四周需要贴防爆膜的面积,就是求这个长方体鱼缸的侧面积,根据长方体侧面积公式:侧面积=(长×高+宽×高)×2,代入数据,即可解答,注意单位名数的换算;
(2)水能将假山石完全淹没,鱼缸中水的高度等于假山石的高度;根据长方体体积公式:体积=长×宽×高,代入数据,求出高是24厘米的长方体的体积,再减去假山石的体积,即可求出水的体积,注意单位名数的换算。
【详解】(1)(60×40+40×40)×2
=(2400+1600)×2
=4000×2
=8000(平方厘米)
8000平方厘米=0.8平方米
答:一共需要贴0.8平方米的防爆膜。
(2)60×40×24-1100
=2400×24-1100
=57600-1100
=56500(立方厘米)
56500立方厘米=56.5立方分米
答:至少需要注入56.5立方分米的水才能将假山石完全淹没。
27.12包
【分析】收纳盒的长为15厘米,宽是14厘米,高是6厘米。收纳盒的长与纸巾的长重合,可以放(15÷5)包纸巾;收纳盒的宽与纸巾的宽重合,可以放(14÷7)包纸巾;收纳盒的高与纸巾的高重合,可以放(6÷3)包纸巾,最后相乘求出收纳盒放置纸巾的总数量,据此解答。
【详解】(15÷5)×(14÷7)×(6÷3)
=3×2×2
=6×2
=12(包)
答:这个收纳盒中最多可以放置12包纸巾。
28.(1)178.1平方米
(2)84立方分米
【分析】(1)由题可知,在房间的四壁和房顶贴上新的墙纸,则用长×宽+长×高×2+宽×高×2-门窗面积=墙纸面积,据此列式解答;
(2)水面上升的体积就是珊瑚石的体积,长方体鱼缸长×宽×水面上升高度=珊瑚石的体积。
【详解】(1)10×5.8+10×4×2+5.8×4×2-6.3
=58+40×2+23.2×2-6.3
=58+80+46.4-6.3
=138+46.4-6.3
=184.4-6.3
=178.1(平方米)
答:装修时至少用了178.1平方米的墙纸。
(2)8×7×(4.5-3)
=56×1.5
=84(立方分米)
答:珊瑚石的体积是84立方分米。
中小学教育资源及组卷应用平台
北师大版五年级下册数学第四单元长方体(二)应用题训练
1.深圳大运中心游泳馆比赛池的长是50米、宽是25米、深是2米。往池里加水至1.8米深,按5元/立方米计算,这池水的水费是多少元?
2.工人叔叔要把一个棱长6厘米的正方体钢坯锻造成一个长9厘米、宽6厘米的长方体零件,这个零件的高是多少厘米?
3.一个正方体油箱,棱长4分米,装满油后倒入一个长8分米、宽2分米的长方体油箱中,油深多少分米?
4.一个长方体的底面是一个周长为30厘米的长方形,高是10厘米,如果它的长宽都是合数,那么这个长方体的体积是多少立方厘米?
5.一个长方体容器,底面长2分米、宽1.5分米,放入一个土豆后水面升高了0.2分米,这个土豆的体积是多少?
6.淘气和笑笑各有一瓶同样多的饮料,淘气倒了3杯,而笑笑只倒了2杯,你认为有可能吗?说一说你的想法。
7.一个无水鱼缸(如图)中放有一块高28厘米,体积为4200立方厘米的假山石,如果自来水管以每分7立方分米的流量向鱼缸内注水,至少要多少分钟才能将假山石完全淹没?
8.一个无盖的玻璃鱼缸,长50厘米,宽30厘米,高35厘米,缸内水位高20厘米(如下图)。
(1)制作这个鱼缸至少需要多少平方厘米的玻璃?
(2)如果向这个鱼缸倒入3000毫升水和一些细沙,这时水面上升到30厘米,倒入了多少立方厘米的细沙(玻璃厚度忽略不计)?
9.如图是一个无盖的长方体的展开图,根据这个展开图用玻璃制作一个玻璃容器。
(1)至少需要多少平方分米的玻璃?
(2)在制作好的容器里倒入5L水和体积和为1立方分米的金鱼,容器里水面的高度是多少分米?(容器的厚度忽略不计)
10.把一块石头放入长4分米、宽3分米、高2分米的装有水的长方体容器内,石头完全浸没在水中,这时水面上升到1.5分米,容器内原来水的高度是1分米,这块石头的体积是多少立方分米?
11.学校修建了一个长50米,宽20米,高1.8米的游泳池。
(1)在池底和四周贴上瓷砖,贴瓷砖的面积是多少平方米?
(2)游泳池中共注水1500立方米,水面距池口多少米?
12.游泳馆新建一个游泳池,长30米、宽20米、深2米。游泳池的四壁和底面铺瓷砖。
(1)需要铺瓷砖的面积是多少平方米?
(2)如果给游泳池注水960立方米,游泳池水深多少米?
13.一个长方体水箱,从里面量得长是30厘米,宽是15厘米。水箱中完全浸没一块石头后,水深20厘米。当取出这块石头后,水深16厘米。这块石头的体积是多少立方分米?
14.下面是一个长方体盒子的展开图。(单位:厘米)
(1)长方体盒子的表面积是多少平方厘米?
(2)长方体盒子的体积是多少立方厘米?
15.仔细观察下图,石块的体积是多少立方厘米?(容器底面是正方形)
16.一个长方体果汁盒从里面量长9厘米,宽6厘米,高19厘米,包装盒上标着“净含量1升”的字样,这个果汁盒能不能装进1升的果汁呢?
17.如图,将一根长48分米的长方体木料截成两段,表面积比原来增加了45平方分米,原来这根木料的体积是多少立方米?
18.一个正方体容器,从里面量,棱长是50厘米,其中水深30厘米。另有一个长、宽、高分别为35厘米、20厘米、20厘米的长方体铁块。把铁块横着放入水中,被完全淹没,此时水位将升高多少分米?
19.如图是一个无盖的长方体玻璃容器。
(1)这个长方体玻璃容器的表面积是多少平方厘米?
(2)如果放进一个铁块并完全浸没在水中(如图所示),1立方厘米的铁块重7.9克,这个铁块有多少克?
20.体育馆计划建一个长10米、宽6米、高25分米的游泳池,请你帮助设计:
(1)它的占地面积是多少平方米?
(2)把它的四周和底面铺上方砖,铺方砖的面积是多少?
(3)建造这个游泳池能挖出多少方土?
21.一个无水的观赏鱼缸中放着一块高为3分米、体积为4立方分米的假山石(如图)。现在需要向鱼缸中注水完全淹没假山石。
(1)至少需要多少升水?
(2)如果取出假山石,水面会下降多少厘米?
22.将如图中的铁皮折弯后焊接成一个无盖的长方体铁桶,这个铁桶最多可以装多少升水?(铁皮厚度不计)
23.健身中心新建的游泳池长50米,宽25米,深2.2米。
(1)这个游泳池最多可蓄水多少立方米?
(2)要在它的四壁和底部铺上瓷砖,铺瓷砖部分的面积是多少平方米?
24.张叔叔要制作一个棱长为15厘米的正方体无盖玻璃鱼缸。
(1)至少需要玻璃多少平方厘米?
(2)这个鱼缸最多可装水多少升?(玻璃的厚度忽略不计)
25.张叔叔用铁皮做了一个长40厘米,宽20厘米,高52厘米的无盖长方体容器(甲),然后给这个容器中倒入高30厘米的水。
(1)张叔叔做这个长方体容器,至少需要铁皮多少平方厘米?(接头处不计)
(2)如果张叔叔将这个容器里的水全部倒入乙容器,乙容器的水面高多少厘米?
26.AI智能模块化鱼缸是一款科技感十足的智能鱼缸,它拥有自动定时喂食、自动清洁等多种功能,让养鱼这件事变得更加简单。张大爷家的智能鱼缸是长60厘米,宽和高都是40厘米的长方体。
(1)鱼缸的四周是钢化玻璃,为了防止玻璃自爆,需要在玻璃上贴一层防爆膜,一共需要贴多少平方米的防爆膜?(损耗忽略不计)
(2)鱼缸中放有一块高为24厘米,体积为1100立方厘米的假山石(如图),如果向鱼缸内注水,那么至少需要注入多少立方分米的水才能将假山石完全淹没?
27.笑笑家有一个收纳盒(如图1),她想把家里散落的小包纸巾(如图2)分别放入收纳盒中(纸巾不能超过收纳盒的上沿且不能挤压)。这个收纳盒中最多可以放置多少包纸巾?(单位:厘米)
28.先认真阅读下面的材料,并从中选择恰当的数学信息解决问题。
光明小学里有个快乐书吧,书吧室内量长10米、宽5.8米、高4米,门窗面积共6.3平方米。书吧服务台旁有一个长8分米、宽7分米、高5分米的长方体鱼缸。今年6月,书吧进行了重新装修:房间的四壁和房顶贴上了新的墙纸,地面重新铺了正方形的地砖,鱼缸(无盖)的棱上贴上了装饰条,鱼缸里还放了美丽的珊瑚石……
(1)装修时至少用了多少平方米的墙纸?
(2)鱼缸里原来水深3分米,放入珊瑚石(完全浸没)后,水面上升到4.5分米,珊瑚石的体积是多少立方分米?(鱼缸的厚度忽略不计)
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
《北师大版五年级下册数学第四单元长方体(二)应用题训练》参考答案
1.11250元
【分析】已知游泳馆比赛池的长、宽和注水的深度,根据长方体的体积公式:V=abh,把数据代入公式,求出注入水的体积;
然后根据单价×数量=总价,用每立方米水的价钱乘水的体积,即可求出这池水的水费。
【详解】50×25×1.8
=1250×1.8
=2250(立方米)
5×2250=11250(元)
答:这池水的水费是11250元。
2.4厘米
【分析】由题意可知,正方体钢坯锻造成长方体零件后体积不变,先根据“正方体的体积=棱长×棱长×棱长”求出钢坯的体积,再根据“长方体的高=长方体的体积÷长÷宽”求出这个零件的高度,据此解答。
【详解】6×6×6÷9÷6
=216÷9÷6
=24÷6
=4(厘米)
答:这个零件的高是4厘米。
3.4分米
【分析】先根据“正方体的体积=棱长×棱长×棱长”求出油的体积,长方体油箱中油的体积和正方体油箱中油的体积相等,长方体油箱中油的深度=油的体积÷长方体油箱的长÷长方体油箱的宽,据此解答。
【详解】4×4×4÷8÷2
=16×4÷8÷2
=64÷8÷2
=8÷2
=4(分米)
答:油深4分米。
4.540立方厘米
【分析】根据长方体周长=(长+宽)×2,可确定长与宽的和是15厘米,15以内的合数是:4、6、8、9、10、12、14、15,则长、宽是9厘米和6厘米。再根据长方体体积=长×宽×高,列式解答即可。
【详解】30÷2=15(厘米)
6和9都是合数且15=9+6,所以长、宽是9厘米、6厘米。
9×6×10
=54×10
=540(立方厘米)
答:这个长方体的体积是540立方厘米。
5.0.6立方分米
【分析】由题意可知,这个土豆的体积等于上升部分水的体积,上升部分水的体积=容器的长×容器的宽×上升部分水的高度,据此解答。
【详解】2×1.5×0.2
=3×0.2
=0.6(立方分米)
答:这个土豆的体积是0.6立方分米。
6.有可能;见详解
【分析】从题意可知:各有一瓶同样多的饮料,说明饮料的体积相同。倒的杯数不同,说明杯子的大小不同,即杯子的容积不同。杯子的容积大,倒的杯数少;杯子的容积小,倒的杯数多。据此解答。
【详解】答:我认为有可能,因为淘气杯子的容积小,倒的杯数多;笑笑杯子的容积大,倒的杯数少。
7.7分钟
【分析】假山石高28厘米,只有水面高度达到28厘米,才能将假山石完全淹没。根据长方体的体积=长×宽×高,求出长45厘米,宽20厘米,高28厘米的长方体的体积(水与假山石的体积之和),再减去假山石的体积,就得注水的体积。根据1立方分米=1000立方厘米,将水的体积换算成立方分米。最后根据每分注水7立方分米,用水的体积除以7即可求出注水时间。
【详解】45×20×28-4200
=25200-4200
=21000(立方厘米)
21000立方厘米=21立方分米
21÷7=3(分钟)
答:至少要7分钟才能将假山石完全淹没。
8.(1)7100平方厘米
(2)12000立方厘米
【分析】(1)这个无盖的玻璃鱼缸有下面和前后左右面积,玻璃的面积=长×宽+长×高×2+宽×高×2,代入数据计算即可,求出需要玻璃的面积。
(2)3000毫升=3000立方厘米。水面从20厘米上升到30厘米,上升了30-20=10厘米,这高10厘米的长方体的体积就是倒入的水和细沙的体积之和。根据长方体的体积(容积)=长×宽×高,代入数据计算,求出体积之和,再减去水的体积,就是沙子的体积。
【详解】(1)50×30+50×35×2+30×35×2
=1500+3500+2100
=7100(平方厘米)
答:制作这个鱼缸至少需要7100平方厘米的玻璃。
(2)3000毫升=3000立方厘米
50×30×(30-20)-3000
=50×30×10-3000
=15000-3000
=12000(立方厘米)
答:倒入了12000立方厘米的细沙。
9.(1)21平方分米
(2)1分米
【分析】(1)由展开图可知,这个长方体的长是3分米。宽是2分米,高是1.5分米,因为是无盖的,所以是求这个长方体5个面的面积和,根据无盖长方体的表面积=长×宽+(长×高+宽×高)×2,把数据代入公式即可求解;
(2)在制作好的容器里倒入5L水和体积和为1立方分米的金鱼,其总体积为5L水的体积和金鱼的体积和,根据长方体的体积公式:V=abh,那么h=V÷ab,把数据代入公式即可解答。
【详解】(1)(3×1.5+2×1.5)×2+3×2
=(4.5+3)×2+3×2
=7.5×2+3×2
=15+6
=21(平方分米)
答:至少需要21平方分米的玻璃。
(2)5L=5立方分米
(5+1)÷(3×2)
=6÷6
=1(分米)
答:容器里水面的高度是1分米。
10.6立方分米
【分析】根据题意,把一块石头完全浸没在水中,这时水面上升到1.5分米,则水面上升了(1.5-1)分米,那么水上升部分的体积就是这块石头的体积,根据长方体的体积公式V=abh,求出这块石头的体积。
【详解】4×3×(1.5-1)
=12×0.5
=6(立方分米)
答:这块石头的体积是6立方分米。
11.(1)1252平方米
(2)0.3米
【分析】(1)根据题意,求贴瓷砖的面积就是求长方体游泳池前后面、左右面和下面共5个面的总面积,根据前后面的面积=长×高×2,左右面的面积=宽×高×2,下面的面积=长×宽,可得:贴瓷砖的面积=长×高×2+宽×高×2+长×宽,据此解答。
(2)游泳池中共注水1500立方米,即水的体积是1500立方米,游泳池中的水呈长方体,长是50米,宽是20米,根据长×宽×高=长方体的体积可知:长方体的体积÷长÷宽=高,即可求到水的高度,再用游泳池的高度减水的高度,即得到水面距池口的米数。据此解答。
【详解】(1)50×1.8×2+20×1.8×2+50×20
=90×2+36×2+1000
=180+72+1000
=252+1000
=1252(平方米)
答:贴瓷砖的面积是1252平方米。
(2)1500÷50÷20
=30÷20
=1.5(米)
1.8-1.5=0.3(米)
答:水面距池口0.3米。
12.(1)800平方米
(2)1.6米
【分析】(1)求铺瓷砖的面积相当于求长方体前后左右和下面5个面的面积和,深相当于长方体的高,铺瓷砖的面积=长×宽+长×深×2+宽×深×2,据此列式解答。
(2)根据长方体的高=体积÷底面积=体积÷(长×宽),列式解答即可。
【详解】(1)30×20+30×2×2+20×2×2
=600+120+80
=800(平方米)
答:需要铺瓷砖的面积是800平方米。
(2)960÷(30×20)
=960÷600
=1.6(米)
答:游泳池水深1.6米。
13.1.8立方分米
【分析】根据题意,石头的体积=下降的水的体积。下降的水的形状是长30厘米,宽15厘米,高(20-16)厘米的长方体,根据长方体的体积=长×宽×高,代入数据计算即可。最后换算成以立方分米为单位的数。
【详解】30×15×(20-16)
=30×15×4
=1800(立方厘米)
=1.8(立方分米)
答:这块石头的体积是1.8立方分米。
14.(1)148平方厘米
(2)120立方厘米
【分析】(1)观察长方体盒子的展开图,可以确定长方体的长6厘米,宽5厘米,高4厘米,根据长方体表面积=(长×宽+长×高+宽×高)×2,列式解答即可;
(2)根据长方体体积=长×宽×高,列式解答。
【详解】(1)表面积:
(平方厘米)
答:长方体盒子的表面积是148平方厘米。
(2)体积:(立方厘米)
答:长方体盒子的体积是120立方厘米。
15.200立方厘米
【分析】看图可知,浸入石块水面上升了(8-6)厘米,水面上升的体积就是石块的体积,根据长方体体积公式,容器底面积×水面上升的高度=石块的体积,据此列式解答。
【详解】
(立方厘米)
答:石块的体积是200立方厘米。
16.能
【分析】根据长方体容积公式:容积=长×宽×高,代入数据,求出长方体果汁盒的容积,在换算成升,再和1升的果汁进行比较,即可解答。
【详解】9×6×19
=54×19
=1026(立方厘米)
1026立方厘米=1.026升
1.026升>1升,这个果汁盒能装进1升果汁。
答:这个果汁盒能装进1升的果汁。
17.1.08立方米
【分析】这根长方体木料截成两段后,表面积比原来增加了2个长方形的面积。已知表面积比原来增加了45平方分米,用45除以2即可求出一个长方形的面积,即横截面的面积。长方体的体积=横截面的面积×长,据此代入数据计算即可。
【详解】45÷2×48
=22.5×48
=1080(立方分米)
1080立方分米=1.08立方米
答:原来这根木料的体积是1.08立方米。
18.0.56分米
【分析】水位上升部分的体积等于放入长方体的体积,利用长方体体积公式:V=abh计算铁块的体积,再除以正方体容器的底面积即可求水位上升的高度。
【详解】35×20×20÷(50×50)
=700×20÷2500
=14000÷2500
=5.6(厘米)
5.6厘米=0.56分米
答:此时水位将升高0.56分米。
19.(1)410平方厘米
(2)790克
【分析】(1)求无盖长方体玻璃容器的表面积,就是求长方体的下面、前后面、左右面共5个面的面积之和;根据“长×宽+长×高×2+宽×高×2”,代入数据计算求解。
(2)从图中可知,长方体玻璃容器中放入一个铁块后,水面上升了(8-6)厘米,那么水上升部分的体积等于铁块的体积;根据长方体的体积公式V=abh,求出这个铁块的体积,再乘每立方厘米铁块的重量,即是这个铁块的总重量。
【详解】(1)10×5+10×12×2+5×12×2
=50+240+120
=410(平方厘米)
答:这个长方体玻璃容器的表面积是410平方厘米。
(2)10×5×(8-6)
=10×5×2
=100(立方厘米)
100×7.9=790(克)
答:这个铁块有790克。
20.(1)60平方米
(2)140平方米
(3)150方
【分析】(1)占地面积指的是底面积,占地面积=长×宽,据此列式解答;
(2)铺方砖的面积=底面积+长×高×2+宽×高×2,据此列式解答,注意统一单位;
(3)根据长方体体积=长×宽×高,即可求出挖出的土的体积,1方=1立方米。
【详解】(1)10×6=60(平方米)
答:它的占地面积是60平方米。
(2)25分米=2.5米
60+10×2.5×2+6×2.5×2
=60+50+30
=140(平方米)
答:铺方砖的面积是140平方米。
(3)10×6×2.5=150(立方米)=150(方)
答:建造这个游泳池能挖出150方土。
21.(1)92升
(2)1.25厘米
【分析】(1)当水完全淹没假山石时,水的体积和假山石的体积恰好为长8分米、宽4分米、高3分米的长方体的体积。要计算至少需要多少升水,先根据:长方体的体积=长×宽×高,算出鱼缸的体积,再减去假山石的体积。
(2)取出假山石后水面下降的高度可以通过假山石的体积除以鱼缸的底面积来计算。
【详解】(1)8×4×3-4
=96-4
=92(立方分米)
92立方分米=92升
答:至少需要92升的水。
(2)4÷(8×4)
=4÷32
=0.125(分米)
0.125分米=1.25厘米
答:如果取出假山石,水面会下降1.25厘米。
22.32升
【分析】通过观察图形可知,这个无盖长方体的底面是正方形,底面周长是80厘米,根据正方形的周长公式可以求出底面边长,底面边长加上高是100厘米,据此可以求出高,然后根据长方体的容积公式:V=abh,把数据代入公式解答。
【详解】底面边长:80÷4=20(厘米)
高:100-20=80(厘米)
20×20×80
=400×80
=32000(立方厘米)
32000立方厘米=32升
答:这条铁桶最多可以装32升水。
23.(1)2750立方米
(2)1580平方米
【分析】(1)根据长方体的容积公式:V=abh,代入数值进行计算即可;
(2)由题意可知,铺瓷砖部分的面积等于长方体五个面的面积,再结合长方体的五个面的面积=(长×高+宽×高)×2+长×宽,据此进行计算即可。
【详解】(1)50×25×2.2
=1250×2.2
=2750(立方米)
答:这个游泳池最多可蓄水2750立方米。
(2)(50×2.2+25×2.2)×2+50×25
=(110+55)×2+1250
=165×2+1250
=330+1250
=1580(平方米)
答:铺瓷砖部分的面积是1580平方米。
24.(1)1125平方厘米
(2)3.375升
【分析】(1)根据题意,要制作一个棱长为15厘米的正方体无盖玻璃鱼缸,求至少需要玻璃的面积,就是求正方体5个面的面积之和,根据“棱长×棱长×5”,代入数据计算求解。
(2)求这个鱼缸最多可装水的体积,就是求正方体的容积;根据正方体的体积(容积)公式V=a3,代入数据计算求解。注意单位的换算:1升=1000立方厘米。
【详解】(1)15×15×5
=225×5
=1125(平方厘米)
答:至少需要玻璃1125平方厘米。
(2)15×15×15
=225×15
=3375(立方厘米)
3375立方厘米=3.375升
答:这个鱼缸最多可装水3.375升。
25.(1)7040平方厘米
(2)16厘米
【分析】(1)无盖的长方体的表面积=长×宽+(长×高+宽×高)×2,据此代入数据计算即可解答;
(2)根据长方体的体积=长×宽×高计算出甲容器中水的体积,再用水的体积除以乙容器的底面积即可求出乙容器的水面高多少厘米。
【详解】(1)2×(40×52+20×52)+40×20
=2×(2080+1040)+40×20
=2×3120+40×20
=6240+800
=7040(平方厘米)
答:至少需要铁皮7040平方厘米。
(2)40×20×30
=800×30
=24000(立方厘米)
24000÷(60×25)
=24000÷1500
=16(厘米)
答:乙容器的水面高16厘米。
26.(1)0.8平方米
(2)56.5立方分米
【分析】(1)求四周需要贴防爆膜的面积,就是求这个长方体鱼缸的侧面积,根据长方体侧面积公式:侧面积=(长×高+宽×高)×2,代入数据,即可解答,注意单位名数的换算;
(2)水能将假山石完全淹没,鱼缸中水的高度等于假山石的高度;根据长方体体积公式:体积=长×宽×高,代入数据,求出高是24厘米的长方体的体积,再减去假山石的体积,即可求出水的体积,注意单位名数的换算。
【详解】(1)(60×40+40×40)×2
=(2400+1600)×2
=4000×2
=8000(平方厘米)
8000平方厘米=0.8平方米
答:一共需要贴0.8平方米的防爆膜。
(2)60×40×24-1100
=2400×24-1100
=57600-1100
=56500(立方厘米)
56500立方厘米=56.5立方分米
答:至少需要注入56.5立方分米的水才能将假山石完全淹没。
27.12包
【分析】收纳盒的长为15厘米,宽是14厘米,高是6厘米。收纳盒的长与纸巾的长重合,可以放(15÷5)包纸巾;收纳盒的宽与纸巾的宽重合,可以放(14÷7)包纸巾;收纳盒的高与纸巾的高重合,可以放(6÷3)包纸巾,最后相乘求出收纳盒放置纸巾的总数量,据此解答。
【详解】(15÷5)×(14÷7)×(6÷3)
=3×2×2
=6×2
=12(包)
答:这个收纳盒中最多可以放置12包纸巾。
28.(1)178.1平方米
(2)84立方分米
【分析】(1)由题可知,在房间的四壁和房顶贴上新的墙纸,则用长×宽+长×高×2+宽×高×2-门窗面积=墙纸面积,据此列式解答;
(2)水面上升的体积就是珊瑚石的体积,长方体鱼缸长×宽×水面上升高度=珊瑚石的体积。
【详解】(1)10×5.8+10×4×2+5.8×4×2-6.3
=58+40×2+23.2×2-6.3
=58+80+46.4-6.3
=138+46.4-6.3
=184.4-6.3
=178.1(平方米)
答:装修时至少用了178.1平方米的墙纸。
(2)8×7×(4.5-3)
=56×1.5
=84(立方分米)
答:珊瑚石的体积是84立方分米。
