北师大版七年级数学下册 期中检测卷(含答案)
文档属性
| 名称 | 北师大版七年级数学下册 期中检测卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1010.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 09:39:04 | ||
图片预览




文档简介
期中检测卷
(范围:第一章-第三章)
一、选择题:本大题共10小题,每小题3分,共30分.
1.下列各式,运算结果为负数的是( )
A. B. C. D.
2.下列图形中,和是同位角的是( )
A. B. C. D.
3.下列计算正确的是( )
A. B. C. D.
4.下列事件是不可能事件的是( )
A.明天会下雨 B.掷一枚硬币正面朝上
C.任意抛掷一枚骰子,点数大于6 D.翻开九年级上册数学书刚好是第24页
5.袁枚的一首诗《苔》在《经典咏流传》的舞台被重新唤醒,“白日不到处,青春恰自来.苔花如米小,也学牡丹开.”若苔花的花粉直径为米,用科学记数法表示,则n为( )
A. B. C.5 D.6
6.如图,直线,直线被直线所截,且,若,,则的度数为( )
A. B. C. D.
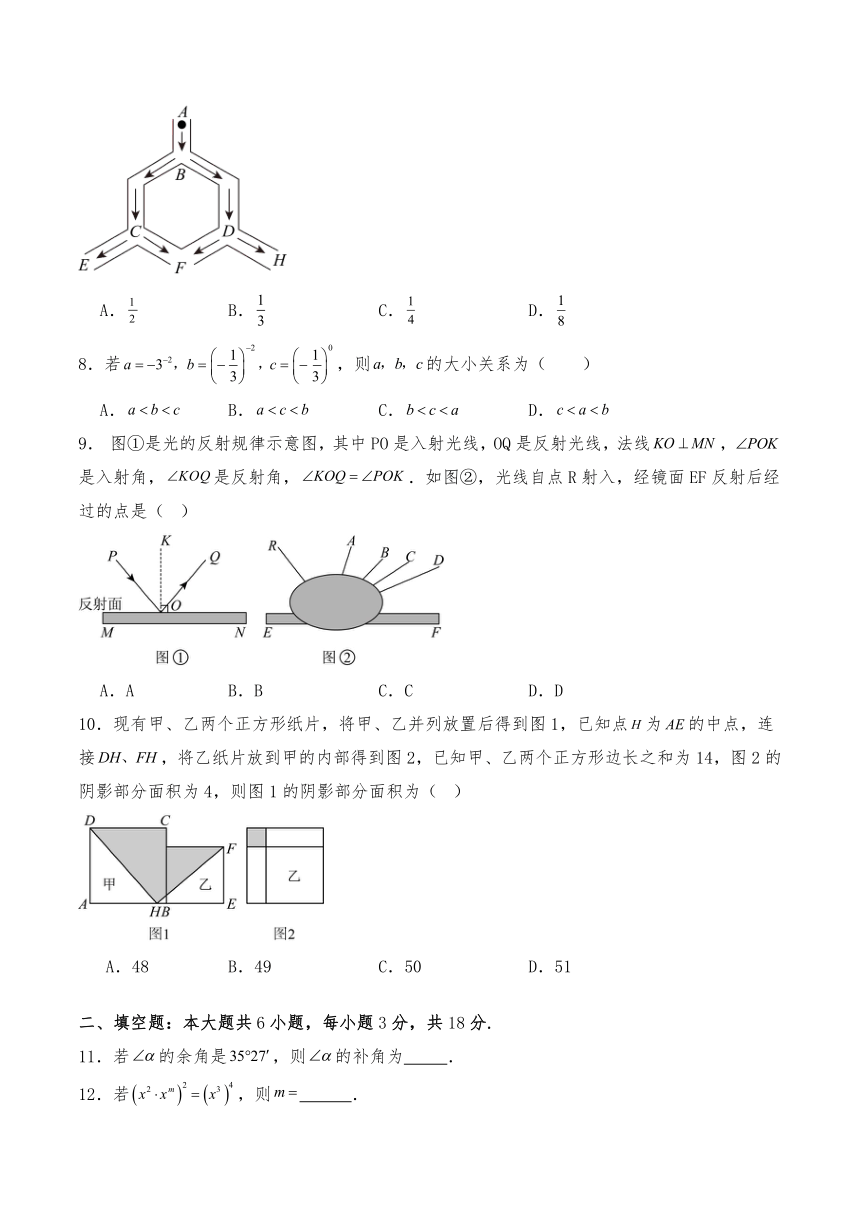
7.如图,一个小球从A点沿制定的轨道下落,在每个交叉口都有向左或向右两种机会相等的结果,那么,小球最终到达F点的概率是( )
A. B. C. D.
8.若,则的大小关系为( )
A. B. C. D.
9. 图①是光的反射规律示意图,其中PO是入射光线,OQ是反射光线,法线,是入射角,是反射角,.如图②,光线自点R射入,经镜面EF反射后经过的点是( )
A.A B.B C.C D.D
10.现有甲、乙两个正方形纸片,将甲、乙并列放置后得到图1,已知点为的中点,连接,将乙纸片放到甲的内部得到图2,已知甲、乙两个正方形边长之和为14,图2的阴影部分面积为4,则图1的阴影部分面积为( )
A.48 B.49 C.50 D.51
二、填空题:本大题共6小题,每小题3分,共18分.
11.若的余角是,则的补角为 .
12.若,则 .
13.如图,已知,则点A到线段的距离为 .
14.2024年农业主导品种主推技术发布,山西的谷子品种“晋谷21号”上榜.为了进一步验证该种子的性能,某生物兴趣小组的同学在相同实验条件下,对其发芽率进行了研究,并得到了以下部分数据:
种子数 30 75 150 200 400 800 1200 2500
发芽数 28 69 141 192 388 778 1167 2435
发芽频率 0.933 0.920 0.940 0.960 0.970 0.973 0.973 0.974
根据上面的数据,估计这种粮食种子在该实验条件下发芽的概率是 .(结果精确到0.01)
15.若关于x的多项式的乘积化简后不含项,则 .
16.若整式是完全平方式,请写出所有满足条件的是 .
三、解答题(一):本大题共4小题,每小题6分,共24分.
17.计算:
(1); (2).
18.先化简再求值:,其中.
19.如图,是的正方形网格,每个小正方形的顶点为格点,线段的两个端点及点C均在格点上.
(1)过点C作的平行线.
(2)过C点作线段的垂线,交于H.
(3)点D是线段与网格线的交点,连结,,比较线段,,的大小: ,理由是 .
20.(1)一只小狗在如下图所示的地板上走来走去,地板是由大小相等的小正方形方砖铺成的.求小狗最终停在灰色方砖上的概率;
(2)一个不透明的袋子中装有1个红球、2个绿球和3个白球,每个球除颜色外其余都相同.将球搅匀后,从中任意摸出1个球.你认为摸到哪种颜色的球的可能性最大?摸到哪种色的球的可能性最小?
四、解答题(二):本大题共3小题,每小题8分,共24分.
21.如下图,已知分别是射线上的点.连接平分平分.
(1)试说明:;
(2)若,求的度数.
22.“一人一盔安全守规,一人一戴平安常在”,如表是某厂质检部门对该厂生产的一批头盔质量检测的情况.
抽取的头盔数 500 1000 1500 2000 3000 4000
合格品数 491 986 1470 1964 2949 3932
合格品频率 0.982 0.986 0.980 a b 0.983
(1)求出表中a=_______,b=_______;
(2)从这批头盔中任意抽取一顶是合格品的概率的估计值是_____(精确到0.01);
(3)如果要出厂49000顶合格的头盔,则该厂估计要生产多少顶头盔?
23.如图,直线,相交于点,以为观察中心,射线表示正北方向,射线表示正东方向,即,射线,的方向如图所示,且.
(1)如图1,
①若射线的方向为北偏东,则射线的方向为_______;
②请说明与互为补角.
(2)如图2,平分,平分,求证:.
五、解答题(三):本大题共2小题,每小题12分,共24分.
24.现定义了一种新运算“,对于任意有理数a,b,c,d,规定,等号右边是通常的减法和乘法运算.例如:.
请解答下列问题
(1)填空:______;
(2)若的代数式中不含x的一次项时,求n的值;
(3)求的值,其中;
(4)如图1,小长方形长为a,宽为b,用5张图1中的小长方形按照图2方式不重叠地放在大长方形内,其中,大长方形中未被覆盖的两个部分(图中阴影部分),设左下角长方形的面积为,右上角长方形的面积为.当,求的值.
25.问题情境:如图1,,,,求度数.
小明的思路是:过P作,通过平行线性质来求.
(1)按小明的思路,易求得的度数为 度;
(2)问题迁移:如图2,,点在射线上运动,记,,当点在、两点之间运动时,问与,之间有何数量关系?请说明理由;
(3)在(2)的条件下,如果点在、两点外侧运动时(点与点、、三点不重合),请直接写出与,之间的数量关系;
(4)问题解决:图3为北斗七星的位置图,将其抽象成图4,其中北斗七星分别标为、、、、、、,将、、、、、、顺次连接,天文小组发现若恰好经过点,且,,,则可以求出的度数.
答案
一、选择题.
1.D
【分析】本题主要考查负数的运算,熟练掌握负数的奇次幂仍是负数是解题的关键.先计算各选项,再根据负数的定义判断.
【详解】解:,故选项A不符合题意;
,故选项B不符合题意;
,故选项C不符合题意;
,故选项D符合题意;
故选D.
2.A
【分析】本题考查同位角,关键是掌握同位角的定义.两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角,由此即可判断.
【详解】解:只有选项A中的和是同位角.
故选:A.
3.D
【分析】本题考查了合并同类项,幂的乘方,同底数幂的乘除法,熟练掌握其运算法则是解题的关键.根据运算法则逐一计算判断即可.
【详解】解:A、 ,原计算错误;
B、 ,原计算错误;
C、 ,原计算错误;
D、,原计算正确;
故选:D.
4.C
【分析】本题考查了随机事件“在一定条件下,可能发生也可能不发生的事件,称为随机事件”、不可能事件“不可能事件的发生的可能性为0”,熟练掌握各定义是解题关键.根据随机事件和不可能事件的定义逐项判断即可得.
【详解】解:A、明天会下雨,是随机事件,则此项不符合题意;
B、掷一枚硬币正面朝上,是随机事件,则此项不符合题意;
C、任意抛掷一枚骰子,点数大于6,是不可能事件,则此项符合题意;
D、翻开九年级上册数学书刚好是第24页,是随机事件,则此项不符合题意;
故选:C.
5.A
【知识点】用科学记数法表示绝对值小于1的数
【分析】将的小数点向右移动6位,则.
本题考查科学记数法表示较小的数,正确记忆科学记数法的形式是解题关键.解:
【详解】解:,
则为.
故选:A.
6.B
【分析】本题主要考查了平行线的性质,对顶角相等,根据平行线的性质得到,然后利用对顶角相等求解即可.
【详解】解:如图所示,
∵,
∴,
∴.
故选:B.
7.A
【分析】本题考查了列举法求概率,先列举出所有等可能得情况,再利用概率公式求解即可.
【详解】解:由图可知,共有,,,4种等可能的情况,
其中小球最终到达F点的情况有,,共2种,
∴小球最终到达F点的概率为.
故选:A.
8.B
【分析】本题考查了零指数幂与负整数指数幂,有理数大小的比较,掌握两个幂的性质是关键;先计算出零指数幂与负整数指数幂,再比较大小即可.
【详解】解:∵,
∴;
故选:B.
9.B
【分析】本题主要考查垂线,角的计算,根据直线的性质补全光线是解题的关键.根据直线的性质画出被遮住的部分,再根据入射角等于反射角作出判断即可.
【详解】解:根据直线的性质补全图2并作出法线,如图所示:
根据图形可以看出是反射光线,
故答案为:B.
10.D
【分析】本题考查完全平方公式的几何背景,设甲正方形的边长为x,乙正方形的边长为y,根据题意得,,两式相加可得,在图1中利用两正方形的面积之和减去两个三角形的面积,代入计算即可.
【详解】解:设甲正方形的边长为x,乙正方形的边长为y,
则,,,
∴,
∴,
∵点H为的中点,
∴,
∵图2的阴影部分面积为,
∴,
∴,
∴图1的阴影部分面积为,
故选:D.
二、填空题.
11.
【分析】本题考查了余角和补角,根据余角的定义先求出,进而根据补角的定义即可求解,掌握余角和补角的定义是解题的关键.
【详解】解:∵的余角是,
∴,
∴的补角,
故答案为:.
12.4
【分析】本题考查幂的运算,运用幂的运算公式化为同底数,即可得到关于m的方程,从而得到答案.
【详解】解:∵,
∴,即,
∴,
解得,
故答案为:4.
13.4
【分析】本题考查点到直线的距离,线段的长为点A到线段的距离,即可解答.
【详解】解:∵,
∴,
∴点A到线段的距离为线段的长,即为4.
故答案为:4.
14.0.97
【分析】本题主要考查利用频率估计概率,大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.利用频率估计概率求解即可.
【详解】解:由题意知,估计这种粮食种子在该实验条件下发芽的概率是0.97,
故答案为:0.97.
15.
【分析】本题考查整式的混合运算,解题的关键在于熟练掌握相关运算法则;根据整式的混合运算顺序,先去括号,再合并同类项后,根据不含项,则该项的系数为0,即可求得a的值.
【详解】解:
,
关于x的多项式的乘积化简后不含项,
,
解得,
故答案为:.
16.或或
【分析】此题考查了完全平方公式,解题的关键是熟练掌握公式的应用.
根据完全平方公式的特点即可求解,
【详解】解:∵完全平方式的形式为
当为,看作,看作时
;
当为,看作,看作时
,
∴,
当为,看作,看作时;
,
∴,
∴,
故答案为:或或.
三、解答题(一).
17.(1)解:原式;
(2)解:原式.
18.解:
,
当时,原式.
19.(1)解:如图所示,即为所求;
(2)解:如图所示,即为所求;
(3)解:由图可知,,理由是垂线段最短.
故答案为:;垂线段最短.
20.解:(1)因为共有15块方砖,其中灰色方砖有5块,所以P(小狗最终停在灰色方砖上).
(2)因为白球的数量最多,红球的数量最少,所以摸到白球的可能性最大,摸到红球的可能性最小.
四、解答题(二).
21.(1)解:因为平分,
所以.
因为,
所以,
所以.
(2)解:因为,
所以.
因为平分,
所以.
因为,
所以,
解得,
所以的度数为.
22.(1)解:,;
(2)解:由表格可知,随着抽取的头盔数量不断增大,任意抽取一个是合格的频率在附近波动,
所以任意抽取的一顶是合格品的概率估计值是;
(3)解:(顶).
答:该厂估计要生产顶头盔.
23.(1)解:①由题意得,
∵,,
∴,
∴射线的方向为南偏东,
故答案为:南偏东;
②,,
,
,,
,
,
与互为补角;
(2)证明:平分,平分,
,,
,
,
,
,
,
即.
,
.
五、解答题(三).
24.(1)解:由题意得,;
(2)解:,
,
,
,
∵代数式中不含x的一次项,
∴,
∴;
(3)解:,
,
,
,
,
∵,
∴原式;
(4)解:根据题意得:,
整理得:,
∴,
,
,
,
,
,
.
25.(1)解:过点作,
∵,,,
∴,
∴,
,
∴,
故答案为:;
(2).
理由:如图,过点作交于,
∵,,,
∴,
∴,,
∴;
(3)如图,当点在的延长线上时,,
过点作交于,
∵,,,
∴,
∴,,
∴;
如图,当点在线段上时,,
过点作交于,
∵,,,
∴,
∴,,
∴.
(4)∵,,
由(2)得:,
∵
∴,
∴,
即的度数为.
(范围:第一章-第三章)
一、选择题:本大题共10小题,每小题3分,共30分.
1.下列各式,运算结果为负数的是( )
A. B. C. D.
2.下列图形中,和是同位角的是( )
A. B. C. D.
3.下列计算正确的是( )
A. B. C. D.
4.下列事件是不可能事件的是( )
A.明天会下雨 B.掷一枚硬币正面朝上
C.任意抛掷一枚骰子,点数大于6 D.翻开九年级上册数学书刚好是第24页
5.袁枚的一首诗《苔》在《经典咏流传》的舞台被重新唤醒,“白日不到处,青春恰自来.苔花如米小,也学牡丹开.”若苔花的花粉直径为米,用科学记数法表示,则n为( )
A. B. C.5 D.6
6.如图,直线,直线被直线所截,且,若,,则的度数为( )
A. B. C. D.
7.如图,一个小球从A点沿制定的轨道下落,在每个交叉口都有向左或向右两种机会相等的结果,那么,小球最终到达F点的概率是( )
A. B. C. D.
8.若,则的大小关系为( )
A. B. C. D.
9. 图①是光的反射规律示意图,其中PO是入射光线,OQ是反射光线,法线,是入射角,是反射角,.如图②,光线自点R射入,经镜面EF反射后经过的点是( )
A.A B.B C.C D.D
10.现有甲、乙两个正方形纸片,将甲、乙并列放置后得到图1,已知点为的中点,连接,将乙纸片放到甲的内部得到图2,已知甲、乙两个正方形边长之和为14,图2的阴影部分面积为4,则图1的阴影部分面积为( )
A.48 B.49 C.50 D.51
二、填空题:本大题共6小题,每小题3分,共18分.
11.若的余角是,则的补角为 .
12.若,则 .
13.如图,已知,则点A到线段的距离为 .
14.2024年农业主导品种主推技术发布,山西的谷子品种“晋谷21号”上榜.为了进一步验证该种子的性能,某生物兴趣小组的同学在相同实验条件下,对其发芽率进行了研究,并得到了以下部分数据:
种子数 30 75 150 200 400 800 1200 2500
发芽数 28 69 141 192 388 778 1167 2435
发芽频率 0.933 0.920 0.940 0.960 0.970 0.973 0.973 0.974
根据上面的数据,估计这种粮食种子在该实验条件下发芽的概率是 .(结果精确到0.01)
15.若关于x的多项式的乘积化简后不含项,则 .
16.若整式是完全平方式,请写出所有满足条件的是 .
三、解答题(一):本大题共4小题,每小题6分,共24分.
17.计算:
(1); (2).
18.先化简再求值:,其中.
19.如图,是的正方形网格,每个小正方形的顶点为格点,线段的两个端点及点C均在格点上.
(1)过点C作的平行线.
(2)过C点作线段的垂线,交于H.
(3)点D是线段与网格线的交点,连结,,比较线段,,的大小: ,理由是 .
20.(1)一只小狗在如下图所示的地板上走来走去,地板是由大小相等的小正方形方砖铺成的.求小狗最终停在灰色方砖上的概率;
(2)一个不透明的袋子中装有1个红球、2个绿球和3个白球,每个球除颜色外其余都相同.将球搅匀后,从中任意摸出1个球.你认为摸到哪种颜色的球的可能性最大?摸到哪种色的球的可能性最小?
四、解答题(二):本大题共3小题,每小题8分,共24分.
21.如下图,已知分别是射线上的点.连接平分平分.
(1)试说明:;
(2)若,求的度数.
22.“一人一盔安全守规,一人一戴平安常在”,如表是某厂质检部门对该厂生产的一批头盔质量检测的情况.
抽取的头盔数 500 1000 1500 2000 3000 4000
合格品数 491 986 1470 1964 2949 3932
合格品频率 0.982 0.986 0.980 a b 0.983
(1)求出表中a=_______,b=_______;
(2)从这批头盔中任意抽取一顶是合格品的概率的估计值是_____(精确到0.01);
(3)如果要出厂49000顶合格的头盔,则该厂估计要生产多少顶头盔?
23.如图,直线,相交于点,以为观察中心,射线表示正北方向,射线表示正东方向,即,射线,的方向如图所示,且.
(1)如图1,
①若射线的方向为北偏东,则射线的方向为_______;
②请说明与互为补角.
(2)如图2,平分,平分,求证:.
五、解答题(三):本大题共2小题,每小题12分,共24分.
24.现定义了一种新运算“,对于任意有理数a,b,c,d,规定,等号右边是通常的减法和乘法运算.例如:.
请解答下列问题
(1)填空:______;
(2)若的代数式中不含x的一次项时,求n的值;
(3)求的值,其中;
(4)如图1,小长方形长为a,宽为b,用5张图1中的小长方形按照图2方式不重叠地放在大长方形内,其中,大长方形中未被覆盖的两个部分(图中阴影部分),设左下角长方形的面积为,右上角长方形的面积为.当,求的值.
25.问题情境:如图1,,,,求度数.
小明的思路是:过P作,通过平行线性质来求.
(1)按小明的思路,易求得的度数为 度;
(2)问题迁移:如图2,,点在射线上运动,记,,当点在、两点之间运动时,问与,之间有何数量关系?请说明理由;
(3)在(2)的条件下,如果点在、两点外侧运动时(点与点、、三点不重合),请直接写出与,之间的数量关系;
(4)问题解决:图3为北斗七星的位置图,将其抽象成图4,其中北斗七星分别标为、、、、、、,将、、、、、、顺次连接,天文小组发现若恰好经过点,且,,,则可以求出的度数.
答案
一、选择题.
1.D
【分析】本题主要考查负数的运算,熟练掌握负数的奇次幂仍是负数是解题的关键.先计算各选项,再根据负数的定义判断.
【详解】解:,故选项A不符合题意;
,故选项B不符合题意;
,故选项C不符合题意;
,故选项D符合题意;
故选D.
2.A
【分析】本题考查同位角,关键是掌握同位角的定义.两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角,由此即可判断.
【详解】解:只有选项A中的和是同位角.
故选:A.
3.D
【分析】本题考查了合并同类项,幂的乘方,同底数幂的乘除法,熟练掌握其运算法则是解题的关键.根据运算法则逐一计算判断即可.
【详解】解:A、 ,原计算错误;
B、 ,原计算错误;
C、 ,原计算错误;
D、,原计算正确;
故选:D.
4.C
【分析】本题考查了随机事件“在一定条件下,可能发生也可能不发生的事件,称为随机事件”、不可能事件“不可能事件的发生的可能性为0”,熟练掌握各定义是解题关键.根据随机事件和不可能事件的定义逐项判断即可得.
【详解】解:A、明天会下雨,是随机事件,则此项不符合题意;
B、掷一枚硬币正面朝上,是随机事件,则此项不符合题意;
C、任意抛掷一枚骰子,点数大于6,是不可能事件,则此项符合题意;
D、翻开九年级上册数学书刚好是第24页,是随机事件,则此项不符合题意;
故选:C.
5.A
【知识点】用科学记数法表示绝对值小于1的数
【分析】将的小数点向右移动6位,则.
本题考查科学记数法表示较小的数,正确记忆科学记数法的形式是解题关键.解:
【详解】解:,
则为.
故选:A.
6.B
【分析】本题主要考查了平行线的性质,对顶角相等,根据平行线的性质得到,然后利用对顶角相等求解即可.
【详解】解:如图所示,
∵,
∴,
∴.
故选:B.
7.A
【分析】本题考查了列举法求概率,先列举出所有等可能得情况,再利用概率公式求解即可.
【详解】解:由图可知,共有,,,4种等可能的情况,
其中小球最终到达F点的情况有,,共2种,
∴小球最终到达F点的概率为.
故选:A.
8.B
【分析】本题考查了零指数幂与负整数指数幂,有理数大小的比较,掌握两个幂的性质是关键;先计算出零指数幂与负整数指数幂,再比较大小即可.
【详解】解:∵,
∴;
故选:B.
9.B
【分析】本题主要考查垂线,角的计算,根据直线的性质补全光线是解题的关键.根据直线的性质画出被遮住的部分,再根据入射角等于反射角作出判断即可.
【详解】解:根据直线的性质补全图2并作出法线,如图所示:
根据图形可以看出是反射光线,
故答案为:B.
10.D
【分析】本题考查完全平方公式的几何背景,设甲正方形的边长为x,乙正方形的边长为y,根据题意得,,两式相加可得,在图1中利用两正方形的面积之和减去两个三角形的面积,代入计算即可.
【详解】解:设甲正方形的边长为x,乙正方形的边长为y,
则,,,
∴,
∴,
∵点H为的中点,
∴,
∵图2的阴影部分面积为,
∴,
∴,
∴图1的阴影部分面积为,
故选:D.
二、填空题.
11.
【分析】本题考查了余角和补角,根据余角的定义先求出,进而根据补角的定义即可求解,掌握余角和补角的定义是解题的关键.
【详解】解:∵的余角是,
∴,
∴的补角,
故答案为:.
12.4
【分析】本题考查幂的运算,运用幂的运算公式化为同底数,即可得到关于m的方程,从而得到答案.
【详解】解:∵,
∴,即,
∴,
解得,
故答案为:4.
13.4
【分析】本题考查点到直线的距离,线段的长为点A到线段的距离,即可解答.
【详解】解:∵,
∴,
∴点A到线段的距离为线段的长,即为4.
故答案为:4.
14.0.97
【分析】本题主要考查利用频率估计概率,大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.利用频率估计概率求解即可.
【详解】解:由题意知,估计这种粮食种子在该实验条件下发芽的概率是0.97,
故答案为:0.97.
15.
【分析】本题考查整式的混合运算,解题的关键在于熟练掌握相关运算法则;根据整式的混合运算顺序,先去括号,再合并同类项后,根据不含项,则该项的系数为0,即可求得a的值.
【详解】解:
,
关于x的多项式的乘积化简后不含项,
,
解得,
故答案为:.
16.或或
【分析】此题考查了完全平方公式,解题的关键是熟练掌握公式的应用.
根据完全平方公式的特点即可求解,
【详解】解:∵完全平方式的形式为
当为,看作,看作时
;
当为,看作,看作时
,
∴,
当为,看作,看作时;
,
∴,
∴,
故答案为:或或.
三、解答题(一).
17.(1)解:原式;
(2)解:原式.
18.解:
,
当时,原式.
19.(1)解:如图所示,即为所求;
(2)解:如图所示,即为所求;
(3)解:由图可知,,理由是垂线段最短.
故答案为:;垂线段最短.
20.解:(1)因为共有15块方砖,其中灰色方砖有5块,所以P(小狗最终停在灰色方砖上).
(2)因为白球的数量最多,红球的数量最少,所以摸到白球的可能性最大,摸到红球的可能性最小.
四、解答题(二).
21.(1)解:因为平分,
所以.
因为,
所以,
所以.
(2)解:因为,
所以.
因为平分,
所以.
因为,
所以,
解得,
所以的度数为.
22.(1)解:,;
(2)解:由表格可知,随着抽取的头盔数量不断增大,任意抽取一个是合格的频率在附近波动,
所以任意抽取的一顶是合格品的概率估计值是;
(3)解:(顶).
答:该厂估计要生产顶头盔.
23.(1)解:①由题意得,
∵,,
∴,
∴射线的方向为南偏东,
故答案为:南偏东;
②,,
,
,,
,
,
与互为补角;
(2)证明:平分,平分,
,,
,
,
,
,
,
即.
,
.
五、解答题(三).
24.(1)解:由题意得,;
(2)解:,
,
,
,
∵代数式中不含x的一次项,
∴,
∴;
(3)解:,
,
,
,
,
∵,
∴原式;
(4)解:根据题意得:,
整理得:,
∴,
,
,
,
,
,
.
25.(1)解:过点作,
∵,,,
∴,
∴,
,
∴,
故答案为:;
(2).
理由:如图,过点作交于,
∵,,,
∴,
∴,,
∴;
(3)如图,当点在的延长线上时,,
过点作交于,
∵,,,
∴,
∴,,
∴;
如图,当点在线段上时,,
过点作交于,
∵,,,
∴,
∴,,
∴.
(4)∵,,
由(2)得:,
∵
∴,
∴,
即的度数为.
同课章节目录
