4.2 全等三角形 课件(共27张PPT)
文档属性
| 名称 | 4.2 全等三角形 课件(共27张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 885.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 00:00:00 | ||
图片预览




文档简介
(共27张PPT)
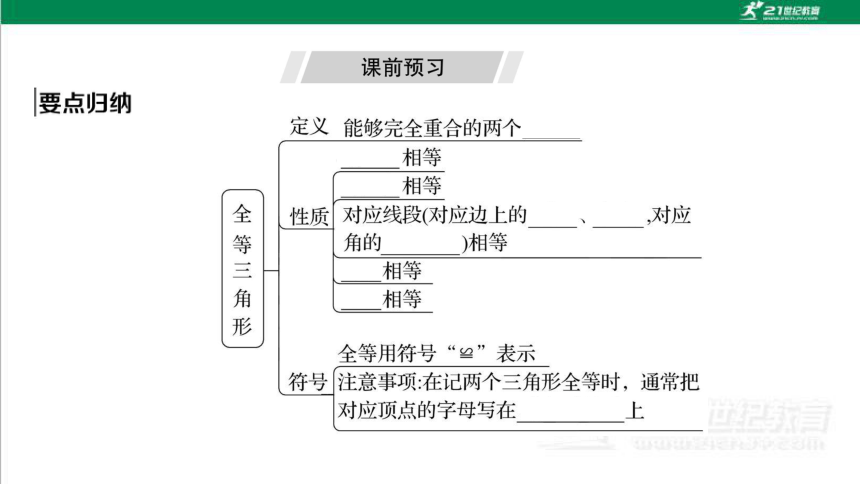
2 全等三角形
课时目标 素养达成
1.通过实例理解全等三角形的概念和特征 几何直观
2.掌握全等三角形对应边相等、对应角相等的性质,并能进
行简单的推理和计算,解决一些实际问题 推理能力、应用意识
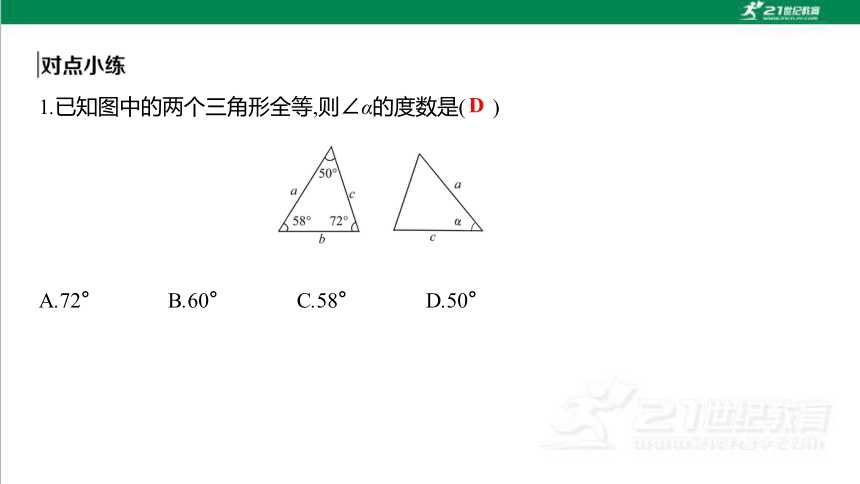
1.已知图中的两个三角形全等,则∠α的度数是( )
A.72° B.60° C.58° D.50°
D
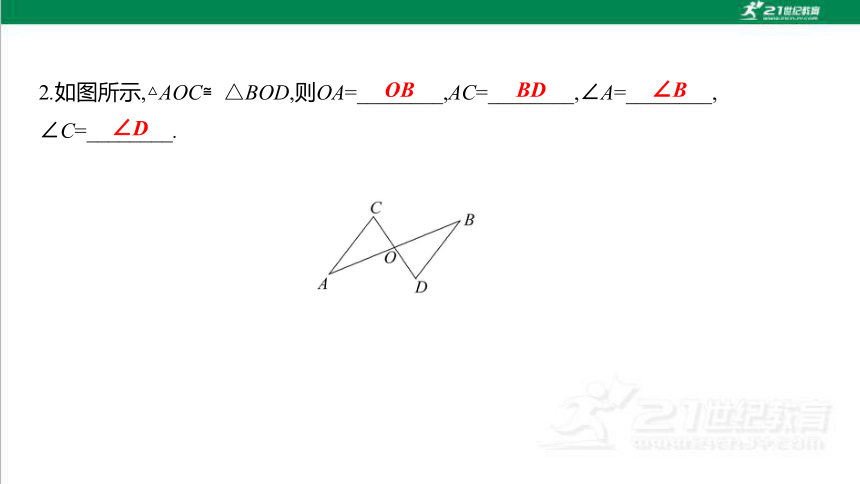
2.如图所示,△AOC≌△BOD,则OA=________,AC=________,∠A=________,
∠C=________.
OB
BD
∠B
∠D
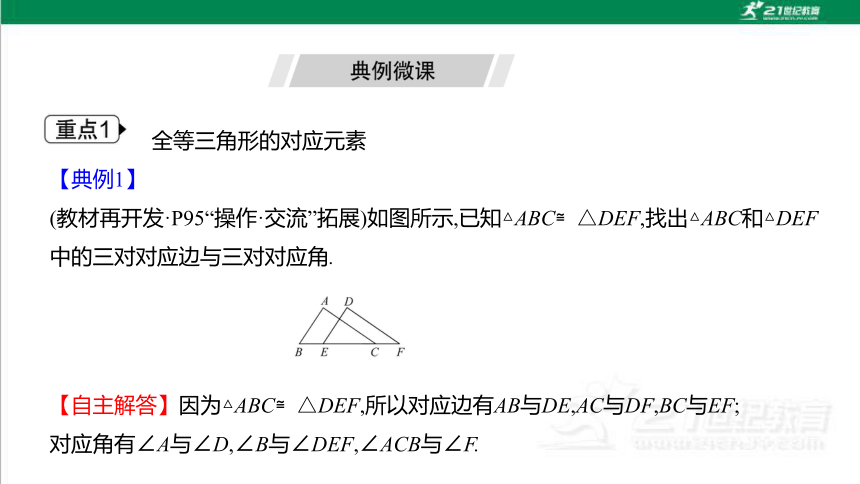
全等三角形的对应元素
【典例1】
(教材再开发·P95“操作·交流”拓展)如图所示,已知△ABC≌△DEF,找出△ABC和△DEF中的三对对应边与三对对应角.
【自主解答】因为△ABC≌△DEF,所以对应边有AB与DE,AC与DF,BC与EF;
对应角有∠A与∠D,∠B与∠DEF,∠ACB与∠F.
1.如图所示,△ABC≌△EFD,则下列说法中,错误的是( )
A.FC=BD
B.EF平行且等于AB
C.AC平行且等于DE
D.CD=ED
D
【解析】A.因为△ABC≌△EFD,
所以FD=BC,
所以FD-CD=BC-CD,
即FC=BD,
B.因为△ABC≌△EFD,
所以∠F=∠B,EF=AB,
所以EF∥AB,
C.因为△ABC≌△EFD,
所以∠ACB=∠EDF,AC=ED,
所以AC∥DE,故A,B,C选项不符合题意.
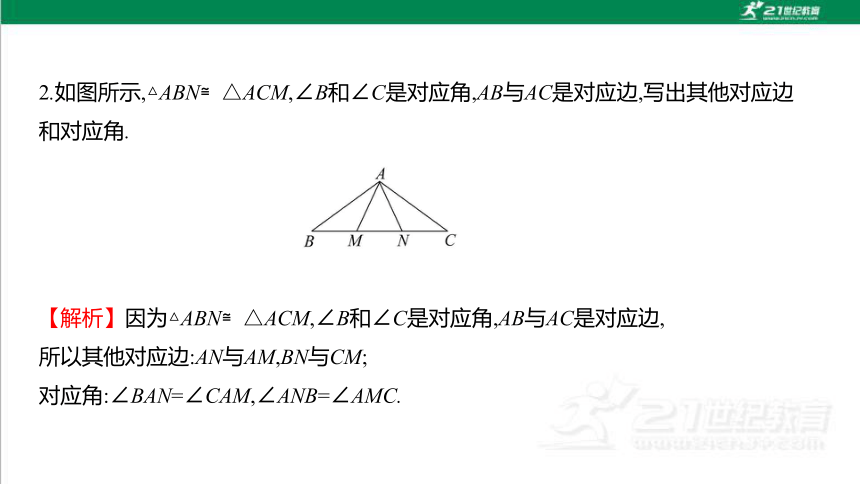
2.如图所示,△ABN≌△ACM,∠B和∠C是对应角,AB与AC是对应边,写出其他对应边和对应角.
【解析】因为△ABN≌△ACM,∠B和∠C是对应角,AB与AC是对应边,
所以其他对应边:AN与AM,BN与CM;
对应角:∠BAN=∠CAM,∠ANB=∠AMC.
1.如图所示,已知△ADC≌△AEB,且AC=5,AD=2,则CE的值为( )
A.1 B.2 C.3 D.4
C
【解析】因为△ADC≌△AEB,
所以AE=AD=2,
因为AC=5,
所以CE=AC-AE=3.
2.(2024·湛江霞山期中)如图所示,△ABC≌△DBE,BD⊥AB,∠D=20°,AC,DE交于点F,
则∠AFE的度数是________.
50°
【解析】因为BD⊥AB,
所以∠ABD=90°,
因为∠D=20°.
所以∠DGB=180°-∠ABD-∠D=70°,所以∠FGA=180°-∠DGB=110°,
因为△ABC≌△DBE,所以∠A=∠D=20°.所以∠AFG=180°-∠A-∠FGA=50°.
3.如图所示,已知△ABC≌△DEB,点E在AB上,AC与BD交于点F.
(1)若AB=6,BC=3,求AE的长.
(2)若∠A=25°,∠C=55°,求∠AED的度数.
【解析】(1)因为△ABC≌△DEB,BC=3,
所以EB=BC=3,
所以AE=AB-EB=6-3=3.
(2)因为△ABC≌△DEB,
所以∠ABC=∠DEB.
因为∠A=25°,∠C=55°,
所以∠ABC=180°-∠A-∠C=180°-25°-55°=100°,
所以∠DEB=100°,所以∠AED=180°-∠DEB=180°-100°=80°.
1.(2024·深圳期中)如图所示的两个三角形全等,则∠1的度数为( )
A.50° B.58° C.60° D.62°
C
【解析】如图所示,
因为∠C=180°-∠A-∠B=180°-58°-62°=60°,
因为两个三角形全等,
所以∠1=∠C=60°.
2.(2024·广州期中)如图所示,△ABC≌△BDE,若AB=12,ED=5,则CD的长为______.
7
【解析】因为△ABC≌△BDE,AB=12,ED=5,
所以AB=BD=12,BC=DE=5,
所以CD=BD-BC=12-5=7.
3.如图所示,△EFG≌△NMH,∠F和∠M是对应角.在△NMH中,MH是最长边.在△EFG中,FG是最长边,EF=2.1 cm,EH=1.2 cm,NH=4.4 cm.
(1)写出其他对应边及对应角.
(2)求线段NM及线段HG的长度.
【解析】(1)因为△EFG≌△NMH,∠F与∠M是对应角,所以EF=NM,EG=NH,FG=MH,∠E=∠N,∠EGF=∠NHM;
(2)因为EF=NM,
EF=2.1 cm,
所以NM=2.1 cm;因为EG=NH,EH+HG=EG,EH=1.2 cm,NH=4.4 cm,
所以HG=EG-EH=NH-EH=4.4-1.2=3.2(cm).
知识点1 全等三角形
1.下列说法中正确的是( )
A.全等三角形的周长和面积分别相等
B.周长相等的两个三角形是全等三角形
C.全等三角形是指形状相同的两个三角形
D.所有的等边三角形都是全等三角形
A
【解析】A.全等三角形的周长和面积分别相等,说法正确,符合题意;
B.周长相等的两个三角形不一定是全等三角形,说法错误,不符合题意;
C.全等三角形是指形状和大小完全相同的两个三角形,说法错误,不符合题意;
D.只有边长相等的等边三角形才是全等三角形,说法错误,不符合题意.
2.(2024·佛山顺德质检)如图所示,点B,C,D在同一直线上,若△ABC ≌△CDE,DE=4,
BD=13,则AB=( )
A.7 B.8 C.9 D.10
C
【解析】因为△ABC≌△CDE,
所以AB=CD,BC=DE=4,
因为BD=13,
所以CD=BD-BC=13-4=9,
所以AB=CD=9.
知识点2 全等三角形性质的运用
3.(2024·汕头濠江二模)如图所示,已知△ABC≌△A'BC',A'C'∥BC,∠C=20°,则∠ABA'
的度数是( )
A.15° B.20° C.25° D.30°
B
【解析】因为△ABC≌△A'BC',∠C=20°,
所以∠C=∠C'=20°,∠ABC=∠A'BC',
所以∠ABA'=∠CBC',
因为A'C'∥BC,
所以∠CBC'=∠C'=20°,
所以∠ABA'=20°.
4.如图所示,△ABC≌△DBE,△ABC的周长为30,AB=9,BE=8,则AC的长是_______.
13
【解析】因为△ABC≌△DBE,BE=8,
所以BC=BE=8,
因为△ABC的周长为30,
所以AB+AC+BC=30,
所以AC=30-AB-BC=13.
5.(2024·汕头潮南区质检)如图所示,在△ABC中,CD⊥AB于点D,E是CD上一点,若
△BDE≌△CDA,AB=14,AC=10,则△BDE的周长为( )
A.22 B.23 C.24 D.26
C
【解析】因为△BDE≌△CDA,
所以DE=DA,BE=CA,
所以△BDE的周长为BD+DE+BE=BD+DA+CA=BA+CA,
因为AB=14,AC=10,
所以△BDE的周长为BA+CA=14+10=24.
6.(2024·广州二中期中)如图所示,△AOB≌△ADC,点B和点C是对应顶点,∠O=∠D=
90°,记∠OAD=α,∠ABO=β,∠ABC=∠ACB,当BC∥OA时,α与β之间的数量关系为( )
A.α=β B.α=2β
C.α+β=90° D.α+2β=180°
B
【解析】因为△AOB≌△ADC,∠O=∠D=90°,
所以∠DAC=∠OAB=90°-∠OBA=90°-β,AB=AC,
所以∠ABC=∠ACB
又因为BC∥OA,
所以∠ABC=∠ACB=∠OAB=90°-β,∠OAC+∠ACB=180°,
因为∠OAC=∠OAD+∠DAC,
所以α+90°-β+90°-β=180°,化简得:α=2β.
7.如图所示,已知△ABF≌△CDE.
(1)若∠B=30°,∠DCF=40°,求∠EFC的度数.
(2)若BD=10,EF=2,求BF的长.
【解析】(1)因为△ABF≌△CDE,所以∠D=∠B=30°,所以∠EFC=∠DCF+∠D=70°.
(2)因为△ABF≌△CDE,所以BF=DE,
所以BF-EF=DE-EF,即BE=DF,
因为BD=10,EF=2,所以BE=(10-2)÷2=4,所以BF=BE+EF=6.
8.(几何直观、推理能力)如图所示,A,D,E三点在同一直线上,且△BAD≌△ACE.
(1)你能说明BD,DE,CE之间的数量关系吗
(2)请你猜想△ABD满足什么条件时,BD∥CE.
【解析】(1)BD=DE+CE.
理由:因为△BAD≌△ACE,所以BD=AE,AD=CE,所以BD=AE=AD+DE=CE+DE,即BD=DE+CE.
(2)△ABD满足∠ADB=90°时,BD∥CE,
理由:因为△BAD≌△ACE,
所以∠E=∠ADB=90°,
所以∠BDE=180°-90°=90°=∠E,
所以BD∥CE.
2 全等三角形
课时目标 素养达成
1.通过实例理解全等三角形的概念和特征 几何直观
2.掌握全等三角形对应边相等、对应角相等的性质,并能进
行简单的推理和计算,解决一些实际问题 推理能力、应用意识
1.已知图中的两个三角形全等,则∠α的度数是( )
A.72° B.60° C.58° D.50°
D
2.如图所示,△AOC≌△BOD,则OA=________,AC=________,∠A=________,
∠C=________.
OB
BD
∠B
∠D
全等三角形的对应元素
【典例1】
(教材再开发·P95“操作·交流”拓展)如图所示,已知△ABC≌△DEF,找出△ABC和△DEF中的三对对应边与三对对应角.
【自主解答】因为△ABC≌△DEF,所以对应边有AB与DE,AC与DF,BC与EF;
对应角有∠A与∠D,∠B与∠DEF,∠ACB与∠F.
1.如图所示,△ABC≌△EFD,则下列说法中,错误的是( )
A.FC=BD
B.EF平行且等于AB
C.AC平行且等于DE
D.CD=ED
D
【解析】A.因为△ABC≌△EFD,
所以FD=BC,
所以FD-CD=BC-CD,
即FC=BD,
B.因为△ABC≌△EFD,
所以∠F=∠B,EF=AB,
所以EF∥AB,
C.因为△ABC≌△EFD,
所以∠ACB=∠EDF,AC=ED,
所以AC∥DE,故A,B,C选项不符合题意.
2.如图所示,△ABN≌△ACM,∠B和∠C是对应角,AB与AC是对应边,写出其他对应边和对应角.
【解析】因为△ABN≌△ACM,∠B和∠C是对应角,AB与AC是对应边,
所以其他对应边:AN与AM,BN与CM;
对应角:∠BAN=∠CAM,∠ANB=∠AMC.
1.如图所示,已知△ADC≌△AEB,且AC=5,AD=2,则CE的值为( )
A.1 B.2 C.3 D.4
C
【解析】因为△ADC≌△AEB,
所以AE=AD=2,
因为AC=5,
所以CE=AC-AE=3.
2.(2024·湛江霞山期中)如图所示,△ABC≌△DBE,BD⊥AB,∠D=20°,AC,DE交于点F,
则∠AFE的度数是________.
50°
【解析】因为BD⊥AB,
所以∠ABD=90°,
因为∠D=20°.
所以∠DGB=180°-∠ABD-∠D=70°,所以∠FGA=180°-∠DGB=110°,
因为△ABC≌△DBE,所以∠A=∠D=20°.所以∠AFG=180°-∠A-∠FGA=50°.
3.如图所示,已知△ABC≌△DEB,点E在AB上,AC与BD交于点F.
(1)若AB=6,BC=3,求AE的长.
(2)若∠A=25°,∠C=55°,求∠AED的度数.
【解析】(1)因为△ABC≌△DEB,BC=3,
所以EB=BC=3,
所以AE=AB-EB=6-3=3.
(2)因为△ABC≌△DEB,
所以∠ABC=∠DEB.
因为∠A=25°,∠C=55°,
所以∠ABC=180°-∠A-∠C=180°-25°-55°=100°,
所以∠DEB=100°,所以∠AED=180°-∠DEB=180°-100°=80°.
1.(2024·深圳期中)如图所示的两个三角形全等,则∠1的度数为( )
A.50° B.58° C.60° D.62°
C
【解析】如图所示,
因为∠C=180°-∠A-∠B=180°-58°-62°=60°,
因为两个三角形全等,
所以∠1=∠C=60°.
2.(2024·广州期中)如图所示,△ABC≌△BDE,若AB=12,ED=5,则CD的长为______.
7
【解析】因为△ABC≌△BDE,AB=12,ED=5,
所以AB=BD=12,BC=DE=5,
所以CD=BD-BC=12-5=7.
3.如图所示,△EFG≌△NMH,∠F和∠M是对应角.在△NMH中,MH是最长边.在△EFG中,FG是最长边,EF=2.1 cm,EH=1.2 cm,NH=4.4 cm.
(1)写出其他对应边及对应角.
(2)求线段NM及线段HG的长度.
【解析】(1)因为△EFG≌△NMH,∠F与∠M是对应角,所以EF=NM,EG=NH,FG=MH,∠E=∠N,∠EGF=∠NHM;
(2)因为EF=NM,
EF=2.1 cm,
所以NM=2.1 cm;因为EG=NH,EH+HG=EG,EH=1.2 cm,NH=4.4 cm,
所以HG=EG-EH=NH-EH=4.4-1.2=3.2(cm).
知识点1 全等三角形
1.下列说法中正确的是( )
A.全等三角形的周长和面积分别相等
B.周长相等的两个三角形是全等三角形
C.全等三角形是指形状相同的两个三角形
D.所有的等边三角形都是全等三角形
A
【解析】A.全等三角形的周长和面积分别相等,说法正确,符合题意;
B.周长相等的两个三角形不一定是全等三角形,说法错误,不符合题意;
C.全等三角形是指形状和大小完全相同的两个三角形,说法错误,不符合题意;
D.只有边长相等的等边三角形才是全等三角形,说法错误,不符合题意.
2.(2024·佛山顺德质检)如图所示,点B,C,D在同一直线上,若△ABC ≌△CDE,DE=4,
BD=13,则AB=( )
A.7 B.8 C.9 D.10
C
【解析】因为△ABC≌△CDE,
所以AB=CD,BC=DE=4,
因为BD=13,
所以CD=BD-BC=13-4=9,
所以AB=CD=9.
知识点2 全等三角形性质的运用
3.(2024·汕头濠江二模)如图所示,已知△ABC≌△A'BC',A'C'∥BC,∠C=20°,则∠ABA'
的度数是( )
A.15° B.20° C.25° D.30°
B
【解析】因为△ABC≌△A'BC',∠C=20°,
所以∠C=∠C'=20°,∠ABC=∠A'BC',
所以∠ABA'=∠CBC',
因为A'C'∥BC,
所以∠CBC'=∠C'=20°,
所以∠ABA'=20°.
4.如图所示,△ABC≌△DBE,△ABC的周长为30,AB=9,BE=8,则AC的长是_______.
13
【解析】因为△ABC≌△DBE,BE=8,
所以BC=BE=8,
因为△ABC的周长为30,
所以AB+AC+BC=30,
所以AC=30-AB-BC=13.
5.(2024·汕头潮南区质检)如图所示,在△ABC中,CD⊥AB于点D,E是CD上一点,若
△BDE≌△CDA,AB=14,AC=10,则△BDE的周长为( )
A.22 B.23 C.24 D.26
C
【解析】因为△BDE≌△CDA,
所以DE=DA,BE=CA,
所以△BDE的周长为BD+DE+BE=BD+DA+CA=BA+CA,
因为AB=14,AC=10,
所以△BDE的周长为BA+CA=14+10=24.
6.(2024·广州二中期中)如图所示,△AOB≌△ADC,点B和点C是对应顶点,∠O=∠D=
90°,记∠OAD=α,∠ABO=β,∠ABC=∠ACB,当BC∥OA时,α与β之间的数量关系为( )
A.α=β B.α=2β
C.α+β=90° D.α+2β=180°
B
【解析】因为△AOB≌△ADC,∠O=∠D=90°,
所以∠DAC=∠OAB=90°-∠OBA=90°-β,AB=AC,
所以∠ABC=∠ACB
又因为BC∥OA,
所以∠ABC=∠ACB=∠OAB=90°-β,∠OAC+∠ACB=180°,
因为∠OAC=∠OAD+∠DAC,
所以α+90°-β+90°-β=180°,化简得:α=2β.
7.如图所示,已知△ABF≌△CDE.
(1)若∠B=30°,∠DCF=40°,求∠EFC的度数.
(2)若BD=10,EF=2,求BF的长.
【解析】(1)因为△ABF≌△CDE,所以∠D=∠B=30°,所以∠EFC=∠DCF+∠D=70°.
(2)因为△ABF≌△CDE,所以BF=DE,
所以BF-EF=DE-EF,即BE=DF,
因为BD=10,EF=2,所以BE=(10-2)÷2=4,所以BF=BE+EF=6.
8.(几何直观、推理能力)如图所示,A,D,E三点在同一直线上,且△BAD≌△ACE.
(1)你能说明BD,DE,CE之间的数量关系吗
(2)请你猜想△ABD满足什么条件时,BD∥CE.
【解析】(1)BD=DE+CE.
理由:因为△BAD≌△ACE,所以BD=AE,AD=CE,所以BD=AE=AD+DE=CE+DE,即BD=DE+CE.
(2)△ABD满足∠ADB=90°时,BD∥CE,
理由:因为△BAD≌△ACE,
所以∠E=∠ADB=90°,
所以∠BDE=180°-90°=90°=∠E,
所以BD∥CE.
同课章节目录
