4.1.1 认识三角形 第1课时 课件(共28张PPT)
文档属性
| 名称 | 4.1.1 认识三角形 第1课时 课件(共28张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 17:11:10 | ||
图片预览






文档简介
(共28张PPT)
1 认识三角形
第1课时
课时目标 素养达成
1.结合具体实例,进一步认识三角形的概念及其基本要素 空间观念、几何直观
2.掌握三角形三个角的关系,会按角将三角形分类 推理能力
1.三角形的定义
(1)定义:由不在同一直线上的三条线段首尾顺次相接所组成的图形.
(2)表示:用符号“△”表示,以A,B,C为顶点的三角形记作△ABC.
2.三角形的内角和定理
文字表述:三角形三个内角的和等于180°.
几何语言:在△ABC中,∠A+∠B+∠C=180°.
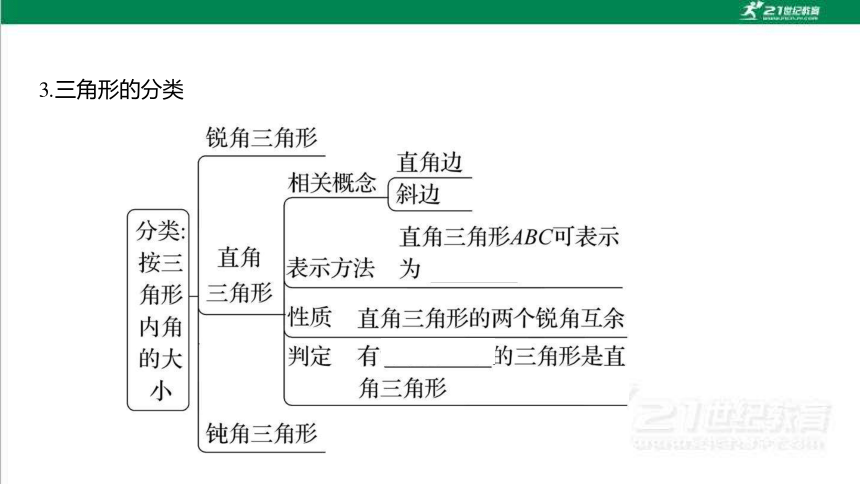
3.三角形的分类
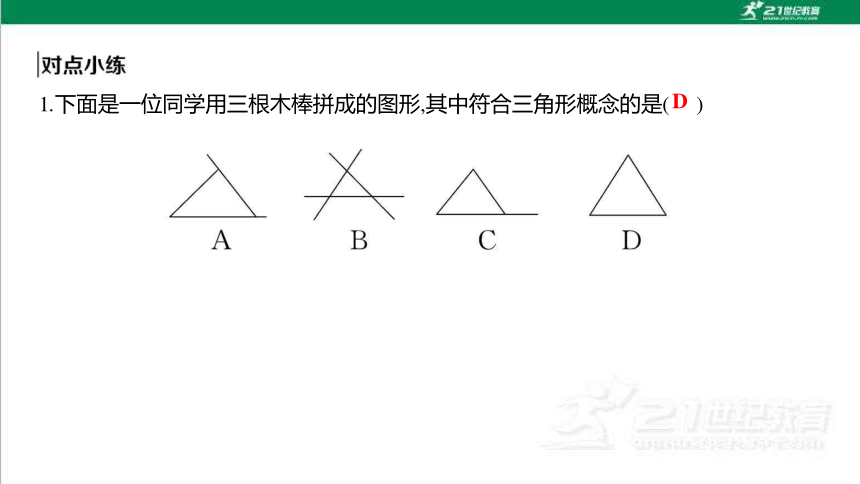
1.下面是一位同学用三根木棒拼成的图形,其中符合三角形概念的是( )
D
2.在△ABC中,若∠A=75°,∠B=40°,则∠C的度数为( )
A.65° B.70° C.75° D.80°
A
3.若一个三角形的两个内角的度数分别为30°和70°,则这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不能确定
A
4.在△ABC中,∠C=90°,∠A=2∠B,则∠B=________.
30°
三角形的计数问题
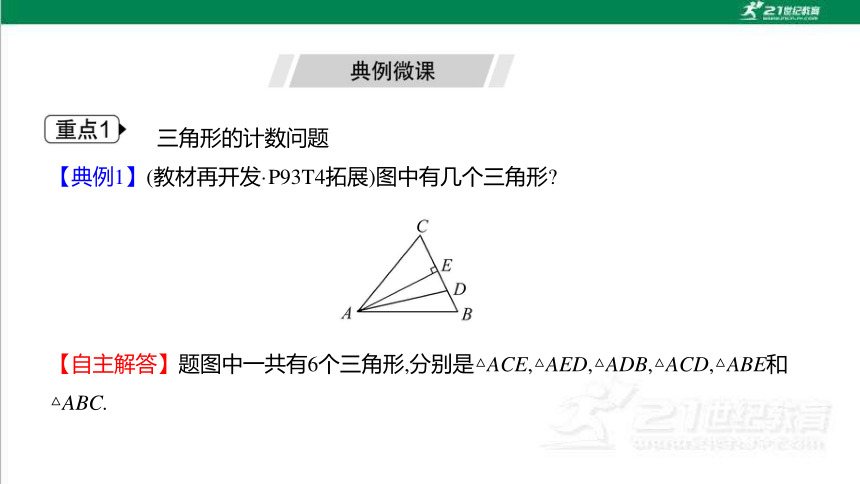
【典例1】(教材再开发·P93T4拓展)图中有几个三角形
【自主解答】题图中一共有6个三角形,分别是△ACE,△AED,△ADB,△ACD,△ABE和△ABC.
1.(2024·肇庆高新质检)在如图所示的图形中,三角形的个数为( )
A.1 B.2 C.3 D.4
C
【解析】BD上有3条线段,所以有三个三角形:△ABD, △ADC,△ABC.
2.(2024·东莞质检)如图所示,在△BCE中,∠CBE所对的边是________;在△AEC中,边AE
所对的角是___________.
EC
∠ACE
【解析】在△BCE中,∠CBE所对的边是EC;在△AEC中,边AE所对的角是∠ACE.
三角形的内角和定理
【典例2】(教材再开发·P85“观察·交流”强化)如图所示,AB∥CD,∠ABE=84°.
(1)求∠EFC的大小.
(2)若∠ABE=3∠DCE,求∠E的大小.
【自主解答】(1)因为AB∥CD,
所以∠DFE=∠ABE=84°,
所以∠EFC=180°-∠DFE=96°.
(2)因为∠ABE=3∠DCE,所以∠DCE=28°,所以∠E=180°-∠EFC-∠DCE=56°.
1.(2024·深圳龙岗质检)若直角三角形的一个锐角等于40°,则它的另一个锐角等于( )
A.50° B.60° C.70° D.140°
A
【解析】因为直角三角形的一个锐角等于40°,
所以它的另一个锐角的度数为90°-40°=50°.
2.(2024·梅州梅县期末)如图所示,在△ABC中,AD是∠BAC的平分线,过点C的射线CE
与AD平行,若∠B=60°,∠ACB=30°,则∠ACE=_______°.
45
1.如图所示,图中直角三角形共有( )
A.1个 B.2个 C.3个 D.4个
C
【解析】题图中直角三角形有Rt△ADB,Rt△BDC,Rt△ABC,共有3个.
2.(2024·河源龙川期末)在△ABC中,∠A+∠B=∠C,则△ABC是_______________.(填“锐
角三角形”“直角三角形”或“钝角三角形”)
直角三角形
【解析】△ABC中,∠A+∠B=∠C,
∠A+∠B+∠C=180°,
所以2∠C=180°,所以∠C=90°,
所以△ABC是直角三角形.
3.如图所示,D是AB上一点,E是AC上一点,∠A+∠B+∠C=180°,∠ADE=70°,∠B=70°,
∠AED=50°,求∠A的度数.
【解析】因为∠ADE=70°,∠B=70°,
所以DE∥BC,所以∠C=∠AED=50°,
因为∠A+∠B+∠C=180°,
所以∠A=180°-∠B-∠C=60°.
知识点1 三角形的概念及表示方法
1.学习完三角形的概念后,小强同学用火柴拼成的图形如下,其中符合三角形概念的
是( )
C
【解析】三角形指的是不在同一直线上的三条线段首尾顺次相接所组成的图形,而A,B,D图形的三根火柴都全部没有或者部分没有首尾相接,所以A,B,D都不符合题意,只有C图形是由三根火柴首尾顺次相接而成的,所以C符合三角形概念.
2.(1)如图所示,点D在△ABC中,写出图中所有的三角形:____________________________.
(2)如图所示,线段BC是△_________和△_________的边.
(3)如图所示,△ABD的3个内角是________________________,三条边是______________.
△ABD,△ADC,△BDC, △ABC
BCD
ACB
∠BAD,∠ABD,∠ADB
AB,AD,BD
【解析】(1)题图中三角形有△ABD,△ADC,△BDC,△ABC.
(2)线段BC是△BCD和△ACB的边.
(3)△ABD的3个内角是∠BAD,∠ABD,∠ADB,三条边是AB,AD,BD.
知识点2 三角形的内角和定理
3.在△ABC中,∠A-∠B=30°,∠C=4∠B,求∠A,∠B,∠C的度数.
【解析】设∠B=x,则∠C=4x,
因为∠A-∠B=30°,所以∠A=30°+x①,
因为∠A+∠B+∠C=180°,
所以∠A+x+4x=180°②,
由①②得,30°+x+x+4x=180°,
解得x=25°,
所以∠A=30°+25°=55°,
∠B=25°,∠C=4x=4×25°=100°.
知识点3 直角三角形的两个锐角互余
4.(2024·高州质检)一个直角三角形,有一个锐角是65°,另一个锐角是_______°.
25
【解析】设另一个锐角的度数为x,
则x+65°=90°,
解得x=25°.
知识点4 三角形按照角分类
5.在△ABC中,若∠A=28°,∠B=62°,则△ABC是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰三角形
B
【解析】在△ABC中,因为∠A=28°,∠B=62°,
所以∠C=180°-28°-62°=90°,
所以三角形是直角三角形.
6.定义:若有一条公共边的两个三角形称为一对“共边三角形”.则图中以BC为公共边
的“共边三角形”有( )
A.1对 B.2对 C.3对 D.4对
C
【解析】根据“共边三角形”的定义:若有一条公共边的两个三角形称为一对“共边三角形”.可知:以BC为公共边的“共边三角形”有△ABC和△BCD,△ABC和△BCE,△BCD和△BCE,共3对.
7.(2024·深圳福田区期末)三角板是重要的作图工具,可以帮助我们作出各种不同的
几何图形,如图所示是由同一副三角板拼凑得到的,则∠EAB的度数为( )
A.50° B.60° C.75° D.85°
C
【解析】由题意得,∠B=45°,∠AEB=60°,
在△ABE中,∠B+∠EAB+∠AEB=180°,
所以∠EAB=180°-∠B-∠AEB=180°-45°-60°=75°.
8.如图所示,在△ABC中,∠B=∠C,点E,F分别在AC,BC边上,延长FE,BA交于点D.
(1)若∠D=30°,∠AED=40°,求∠EFC的度数.
(2)若∠D=∠AED,求证DF⊥BC.
【解析】(1)因为∠D=30°,∠AED=40°,
在△ADE中,∠DAE+∠D+∠AED=180°,
所以∠DAE=180°-∠D-∠AED=110°,
所以∠BAC=180°-∠DAE=70°,
在△ABC中,∠BAC+∠B+∠C=180°,所以∠B+∠C=110°.
因为∠B=∠C,所以∠C=55°,
在△EFC中,∠FEC=∠AED=40°,∠EFC+∠C+∠FEC=180°,
所以∠EFC=180°-∠C-∠FEC,所以∠EFC=85°.
(2)证明:设∠D=∠AED=α,
在△ADE中,∠DAE+∠D+∠AED=180°,
所以∠DAE=180°-∠D-∠AED=180°-2α,
所以∠BAC=180°-∠DAE=2α,
在△ABC中,∠BAC+∠B+∠C=180°,
所以∠B+∠C=180°-2α.
因为∠B=∠C,所以∠C=90°-α,
在△EFC中,∠FEC=∠AED=α,∠EFC+∠C+∠FEC=180°,
所以∠EFC=180°-∠C-∠FEC,
所以∠EFC=180°-(90°-α)-α=90°,所以DF⊥BC.
1 认识三角形
第1课时
课时目标 素养达成
1.结合具体实例,进一步认识三角形的概念及其基本要素 空间观念、几何直观
2.掌握三角形三个角的关系,会按角将三角形分类 推理能力
1.三角形的定义
(1)定义:由不在同一直线上的三条线段首尾顺次相接所组成的图形.
(2)表示:用符号“△”表示,以A,B,C为顶点的三角形记作△ABC.
2.三角形的内角和定理
文字表述:三角形三个内角的和等于180°.
几何语言:在△ABC中,∠A+∠B+∠C=180°.
3.三角形的分类
1.下面是一位同学用三根木棒拼成的图形,其中符合三角形概念的是( )
D
2.在△ABC中,若∠A=75°,∠B=40°,则∠C的度数为( )
A.65° B.70° C.75° D.80°
A
3.若一个三角形的两个内角的度数分别为30°和70°,则这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不能确定
A
4.在△ABC中,∠C=90°,∠A=2∠B,则∠B=________.
30°
三角形的计数问题
【典例1】(教材再开发·P93T4拓展)图中有几个三角形
【自主解答】题图中一共有6个三角形,分别是△ACE,△AED,△ADB,△ACD,△ABE和△ABC.
1.(2024·肇庆高新质检)在如图所示的图形中,三角形的个数为( )
A.1 B.2 C.3 D.4
C
【解析】BD上有3条线段,所以有三个三角形:△ABD, △ADC,△ABC.
2.(2024·东莞质检)如图所示,在△BCE中,∠CBE所对的边是________;在△AEC中,边AE
所对的角是___________.
EC
∠ACE
【解析】在△BCE中,∠CBE所对的边是EC;在△AEC中,边AE所对的角是∠ACE.
三角形的内角和定理
【典例2】(教材再开发·P85“观察·交流”强化)如图所示,AB∥CD,∠ABE=84°.
(1)求∠EFC的大小.
(2)若∠ABE=3∠DCE,求∠E的大小.
【自主解答】(1)因为AB∥CD,
所以∠DFE=∠ABE=84°,
所以∠EFC=180°-∠DFE=96°.
(2)因为∠ABE=3∠DCE,所以∠DCE=28°,所以∠E=180°-∠EFC-∠DCE=56°.
1.(2024·深圳龙岗质检)若直角三角形的一个锐角等于40°,则它的另一个锐角等于( )
A.50° B.60° C.70° D.140°
A
【解析】因为直角三角形的一个锐角等于40°,
所以它的另一个锐角的度数为90°-40°=50°.
2.(2024·梅州梅县期末)如图所示,在△ABC中,AD是∠BAC的平分线,过点C的射线CE
与AD平行,若∠B=60°,∠ACB=30°,则∠ACE=_______°.
45
1.如图所示,图中直角三角形共有( )
A.1个 B.2个 C.3个 D.4个
C
【解析】题图中直角三角形有Rt△ADB,Rt△BDC,Rt△ABC,共有3个.
2.(2024·河源龙川期末)在△ABC中,∠A+∠B=∠C,则△ABC是_______________.(填“锐
角三角形”“直角三角形”或“钝角三角形”)
直角三角形
【解析】△ABC中,∠A+∠B=∠C,
∠A+∠B+∠C=180°,
所以2∠C=180°,所以∠C=90°,
所以△ABC是直角三角形.
3.如图所示,D是AB上一点,E是AC上一点,∠A+∠B+∠C=180°,∠ADE=70°,∠B=70°,
∠AED=50°,求∠A的度数.
【解析】因为∠ADE=70°,∠B=70°,
所以DE∥BC,所以∠C=∠AED=50°,
因为∠A+∠B+∠C=180°,
所以∠A=180°-∠B-∠C=60°.
知识点1 三角形的概念及表示方法
1.学习完三角形的概念后,小强同学用火柴拼成的图形如下,其中符合三角形概念的
是( )
C
【解析】三角形指的是不在同一直线上的三条线段首尾顺次相接所组成的图形,而A,B,D图形的三根火柴都全部没有或者部分没有首尾相接,所以A,B,D都不符合题意,只有C图形是由三根火柴首尾顺次相接而成的,所以C符合三角形概念.
2.(1)如图所示,点D在△ABC中,写出图中所有的三角形:____________________________.
(2)如图所示,线段BC是△_________和△_________的边.
(3)如图所示,△ABD的3个内角是________________________,三条边是______________.
△ABD,△ADC,△BDC, △ABC
BCD
ACB
∠BAD,∠ABD,∠ADB
AB,AD,BD
【解析】(1)题图中三角形有△ABD,△ADC,△BDC,△ABC.
(2)线段BC是△BCD和△ACB的边.
(3)△ABD的3个内角是∠BAD,∠ABD,∠ADB,三条边是AB,AD,BD.
知识点2 三角形的内角和定理
3.在△ABC中,∠A-∠B=30°,∠C=4∠B,求∠A,∠B,∠C的度数.
【解析】设∠B=x,则∠C=4x,
因为∠A-∠B=30°,所以∠A=30°+x①,
因为∠A+∠B+∠C=180°,
所以∠A+x+4x=180°②,
由①②得,30°+x+x+4x=180°,
解得x=25°,
所以∠A=30°+25°=55°,
∠B=25°,∠C=4x=4×25°=100°.
知识点3 直角三角形的两个锐角互余
4.(2024·高州质检)一个直角三角形,有一个锐角是65°,另一个锐角是_______°.
25
【解析】设另一个锐角的度数为x,
则x+65°=90°,
解得x=25°.
知识点4 三角形按照角分类
5.在△ABC中,若∠A=28°,∠B=62°,则△ABC是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰三角形
B
【解析】在△ABC中,因为∠A=28°,∠B=62°,
所以∠C=180°-28°-62°=90°,
所以三角形是直角三角形.
6.定义:若有一条公共边的两个三角形称为一对“共边三角形”.则图中以BC为公共边
的“共边三角形”有( )
A.1对 B.2对 C.3对 D.4对
C
【解析】根据“共边三角形”的定义:若有一条公共边的两个三角形称为一对“共边三角形”.可知:以BC为公共边的“共边三角形”有△ABC和△BCD,△ABC和△BCE,△BCD和△BCE,共3对.
7.(2024·深圳福田区期末)三角板是重要的作图工具,可以帮助我们作出各种不同的
几何图形,如图所示是由同一副三角板拼凑得到的,则∠EAB的度数为( )
A.50° B.60° C.75° D.85°
C
【解析】由题意得,∠B=45°,∠AEB=60°,
在△ABE中,∠B+∠EAB+∠AEB=180°,
所以∠EAB=180°-∠B-∠AEB=180°-45°-60°=75°.
8.如图所示,在△ABC中,∠B=∠C,点E,F分别在AC,BC边上,延长FE,BA交于点D.
(1)若∠D=30°,∠AED=40°,求∠EFC的度数.
(2)若∠D=∠AED,求证DF⊥BC.
【解析】(1)因为∠D=30°,∠AED=40°,
在△ADE中,∠DAE+∠D+∠AED=180°,
所以∠DAE=180°-∠D-∠AED=110°,
所以∠BAC=180°-∠DAE=70°,
在△ABC中,∠BAC+∠B+∠C=180°,所以∠B+∠C=110°.
因为∠B=∠C,所以∠C=55°,
在△EFC中,∠FEC=∠AED=40°,∠EFC+∠C+∠FEC=180°,
所以∠EFC=180°-∠C-∠FEC,所以∠EFC=85°.
(2)证明:设∠D=∠AED=α,
在△ADE中,∠DAE+∠D+∠AED=180°,
所以∠DAE=180°-∠D-∠AED=180°-2α,
所以∠BAC=180°-∠DAE=2α,
在△ABC中,∠BAC+∠B+∠C=180°,
所以∠B+∠C=180°-2α.
因为∠B=∠C,所以∠C=90°-α,
在△EFC中,∠FEC=∠AED=α,∠EFC+∠C+∠FEC=180°,
所以∠EFC=180°-∠C-∠FEC,
所以∠EFC=180°-(90°-α)-α=90°,所以DF⊥BC.
同课章节目录
