4.1.2 认识三角形 第2课时 课件(共29张PPT)
文档属性
| 名称 | 4.1.2 认识三角形 第2课时 课件(共29张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 720.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 17:09:33 | ||
图片预览







文档简介
(共29张PPT)
1 认识三角形
第2课时
课时目标 素养达成
掌握三角形三条边之间的数量关系,会按边将三角形分类 空间观念、几何直观、推理能力
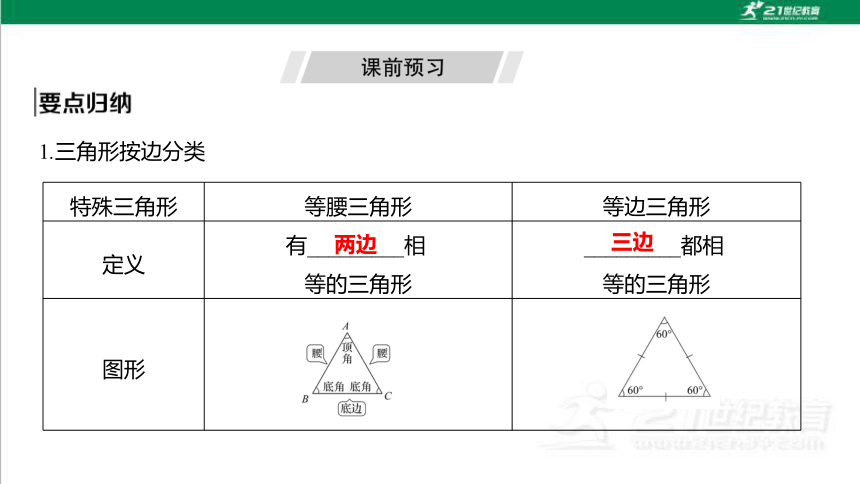
1.三角形按边分类
特殊三角形 等腰三角形 等边三角形
定义 有_________相
等的三角形 _________都相
等的三角形
图形
两边
三边
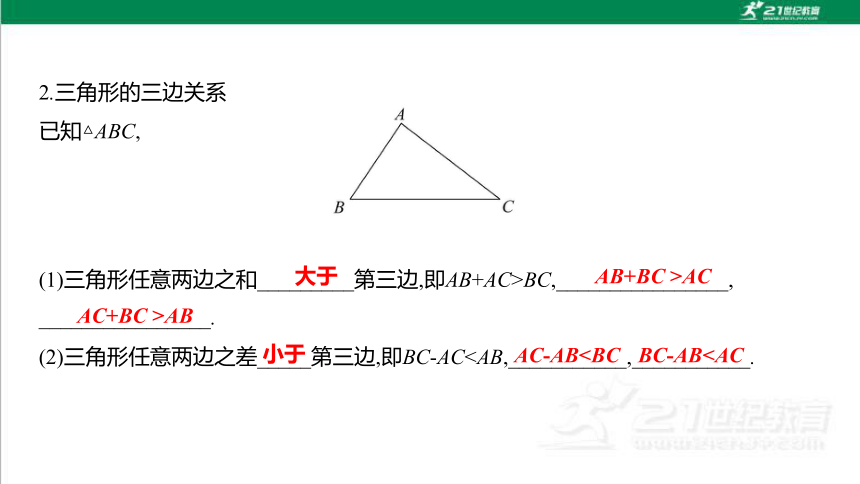
2.三角形的三边关系
已知△ABC,
(1)三角形任意两边之和_________第三边,即AB+AC>BC,________________,
________________.
(2)三角形任意两边之差_____第三边,即BC-AC 大于
AB+BC >AC
AC+BC >AB
小于
AC-ABBC-AB1.如图所示是三角形按常见关系进行分类的图,则关于P,Q区域的说法正确的是( )
A.P是等边三角形,Q是等腰三角形
B.P是等腰三角形,Q是等边三角形
C.P是直角三角形,Q是锐角三角形
D.P是钝角三角形,Q是等腰三角形
B
2.下列长度的三段钢条,不能组成一个三角形框架的是(单位:cm)( )
A.2,3,4 B.3,7,7
C.2,2,6 D.4,6,8
C
三角形的三边关系及应用
【典例1】(教材再开发·P93T5拓展)(2024·深圳福田期中)已知△ABC的三边长为a,b,c,且a,b,c都是整数.
(1)若a=2,b=5,且c为偶数.求△ABC的周长.
(2)化简:|a-b+c|-|b-c-a|+|a+b+c|.
【自主解答】(1)因为a=2,b=5,
所以5-2因为c为偶数,所以c=4或6,
当c=4时,△ABC的周长为a+b+c=2+5+4=11;
当c=6时,△ABC的周长为a+b+c=2+5+6=13,
综上所述,△ABC的周长为11或13.
(2)因为△ABC的边长为a,b,c,所以a+c>b,
所以|a-b+c|-|b-c-a|+|a+b+c|
=a+c-b-(a+c-b)+a+b+c
=a+c-b-a-c+b+a+b+c
=a+b+c.
1.(2024·广州越秀质检)下列长度的三条线段,能组成三角形的是( )
A.5,3,8 B.4,3,5
C.2,4,6 D.3,6,9
【解析】因为8=5+3,与两边之和大于第三边不一致,所以A不符合题意;
因为4+3=7>5,与两边之和大于第三边一致,
所以B符合题意;
因为4+2=6,不能组成三角形,
所以C不符合题意;
因为3+6=9,不能组成三角形,所以D不符合题意.
B
2.(2024·韶关模拟)如图所示,人字梯的支架AB,AC的长度都为2 m(连接处的长度忽略
不计),则B,C两点之间的距离可能是( )
A.3 m B.4.2 m
C.5 m D.6 m
A
【解析】因为AC=AB=2 m,
所以2-23.(2024·深圳罗湖期末)如图所示,下面的四个盒子中,每个盒子里都有两根小棒,把其
中的一根小棒用剪刀按图中所示的位置剪成两段,这两段小棒再与另一根小棒首尾
相接,能够围成一个三角形的是( )
B
【解析】A.图中小棒被剪刀剪成两段,这两段加起来比下面那根木棒短,不符合三角形的三边关系,无法围成三角形;
B.图中小棒被剪刀剪成两段,这两段加起来比上面那根木棒长,这两段相减比上面那根木棒短,符合三角形的三边关系,可以围成三角形;
C.图中小棒被剪刀剪成两段,这两段相减比下面那根木棒还长,不符合三角形的三边关系,无法围成三角形;
D.图中小棒被剪刀剪成两段,这两段加起来和上面那根木棒相等,不符合三角形的三边关系,无法围成三角形.
等腰三角形
【典例2】(教材再开发·P88“思考·交流”强化)已知x,y满足|4-x|+|y-6|=0,则以x,y的值为两边长的等腰三角形的周长是( )
A.14或16 B.14
C.16 D.以上答案均不对
【自主解答】选A.根据题意得,4-x=0,y-6=0,解得x=4,y=6,
①4是腰长时,三角形的三边长分别为4,4,6,
因为4+4=8,
所以三角形的周长为14;
②4是底边时,三角形的三边长分别为4,6,6,
能组成三角形,周长为4+6+6=16,
所以三角形的周长为14或16.
1.等腰三角形的周长为16,其中腰长为x,则x不可能为( )
A.4 B.5 C.6 D.7
A
【解析】A.当x=4时,三边长分别为4,4,8,
因为4+4=8,
所以不能围成三角形,
所以腰长不能为4,故该选项符合题意;
B.当x=5时,三边长分别为5,5,6,
因为5+5>6,
所以能围成三角形,
所以腰长能为5,故该选项不符合题意;
C.当x=6时,三边长分别为6,6,4,
因为4+6>6,
所以能围成三角形,
所以腰长能为6,故该选项不符合题意;
D.当x=7时,三边长分别为7,7,2,
因为7+2>7,
所以能围成三角形,
所以腰长能为7,故该选项不符合题意.
2.等腰三角形的一边等于3,一边等于6,则它的周长等于_______.
15
【解析】当3为腰,6为底时,3+3=6,不能构成等腰三角形;
当6为腰,3为底时,3+6>6,能构成等腰三角形,周长为3+6+6=15.
1.(2024·揭阳惠来期末)以下列长度的各组线段为边,能组成三角形的是( )
A.3 cm,7 cm,4 cm B.2 cm,3 cm,6 cm
C.5 cm,6 cm,7 cm D.1 cm,2 cm,3 cm
C
【解析】A.3+4=7,不能组成三角形,不符合题意;
B.2+3<6,不能组成三角形,不符合题意;
C.5+6>7,能组成三角形,符合题意;
D.1+2=3,不能组成三角形,不符合题意.
2.小明有两根长3 cm,7 cm的木棒,他想以这两根木棒为边做一个等腰三角形,还需再
选用一根长______cm的木棒.
7
【解析】当3 cm为腰长时,因为3+3=6<7,不符合三角形的三边关系,所以舍去;
当7 cm为腰长时,符合三角形的三边关系,符合题意.所以再选用一根长7 cm的木棒.
3.已知△ABC的三边长是a,b,c.
(1)若a=6,b=8,且三角形的周长是小于22的偶数,求c的值.
(2)化简|a+b-c|+|c-a-b|.
【解析】(1)因为a,b,c是△ABC的三边,a=6,b=8,所以2因为三角形的周长是小于22的偶数,所以2(2)|a+b-c|+|c-a-b|=a+b-c-c+a+b=2a+2b-2c.
知识点1 三角形按边分类
1.下列分类正确的是( )
A.三角形可分为等腰三角形、等边三角形
B.三角形可分为三边各不相等的三角形、等腰三角形以及等边三角形
C.三角形可分为三边各不相等的三角形和等边三角形
D.三角形可分为三边各不相等的三角形和等腰三角形
D
【解析】三角形可分为三边各不相等的三角形和等腰三角形.
2.设a,b,c分别是△ABC的三边长,且(a+b-c)(a-b)=0,则△ABC的形状是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰三角形
D
【解析】因为(a+b-c)(a-b)=0,
a+b>c,所以a+b-c>0,所以a-b=0,
所以a=b,所以△ABC为等腰三角形.
知识点2 三角形的三边关系
3.(2024·东莞期末)下列长度的各组线段中,能构成三角形的是( )
A.2,5,8 B.3,3,6 C.4,4,7 D.4,5,9
C
【解析】三角形的三边关系定理:任意两边之和大于第三边.
A.2+5=7<8,不能构成三角形,此项不符题意;
B.3+3=6,不能构成三角形,此项不符题意;
C.4+4>7,能构成三角形,此项符合题意;
D.4+5=9,不能构成三角形,此项不符题意.
4.(2024·深圳福田期中)已知三角形两边长分别为6和3,第三边的长是整数,这个三角
形周长的最小值是_______.
13
【解析】设第三边长为a,所以3因为第三边长为整数,
所以最小整数为4,
所以周长最小为6+4+3=13.
5.(2023·河北中考)四边形ABCD的边长如图所示,对角线AC的长度随四边形形状的改
变而变化.当△ABC为等腰三角形时,对角线AC的长为( )
A.2 B.3 C.4 D.5
B
【解析】因为△ABC为等腰三角形,
所以AB=AC或AC=BC,
当AC=BC=4时,AD+CD=AC=4,此时不满足三角形三边关系定理,
当AC=AB=3时,满足三角形三边关系定理,
所以AC=3.
6.(2024·佛山禅城区期末)如图所示,△ABC被木板遮住了一部分,其中AB=5,则AC+BC
的值可能是( )
A.3 B.4 C.5 D.6
D
【解析】因为三角形两边之和大于第三边,
所以AC+BC>AB,
因为AB=5,所以AC+BC>5.
7.(2024·深圳南山区期中)设a,b,c为△ABC的三边,化简|a-b+c|-|a+b-c|-|a-b-c|=
___________.
a-3b+c
【解析】因为a,b,c为△ABC的三边,
所以a+c>b,a+b>c,b+c>a,
所以a-b+c>0,a+b-c>0,a-b-c<0,
所以|a-b+c|-|a+b-c|-|a-b-c|=a-b+c-(a+b-c)+(a-b-c)=a-b+c-a-b+c+a-b-c=a-3b+c.
8.已知a,b,c是△ABC的三边长,且a,b,c都是整数.
(1)若a,b,c满足|a-b|+|b-c|=0,试判断△ABC的形状.
(2)若a=2,b=5,且c是奇数,试判断△ABC的形状.
【解析】(1)因为a,b,c满足|a-b|+|b-c|=0,所以a-b=0,b-c=0,
所以a=b=c,
所以△ABC的形状是等边三角形.
(2)因为a=2,b=5,所以5-2因为c是奇数,
所以c=5,所以b=c,
所以△ABC的形状是等腰三角形.
1 认识三角形
第2课时
课时目标 素养达成
掌握三角形三条边之间的数量关系,会按边将三角形分类 空间观念、几何直观、推理能力
1.三角形按边分类
特殊三角形 等腰三角形 等边三角形
定义 有_________相
等的三角形 _________都相
等的三角形
图形
两边
三边
2.三角形的三边关系
已知△ABC,
(1)三角形任意两边之和_________第三边,即AB+AC>BC,________________,
________________.
(2)三角形任意两边之差_____第三边,即BC-AC
AB+BC >AC
AC+BC >AB
小于
AC-AB
A.P是等边三角形,Q是等腰三角形
B.P是等腰三角形,Q是等边三角形
C.P是直角三角形,Q是锐角三角形
D.P是钝角三角形,Q是等腰三角形
B
2.下列长度的三段钢条,不能组成一个三角形框架的是(单位:cm)( )
A.2,3,4 B.3,7,7
C.2,2,6 D.4,6,8
C
三角形的三边关系及应用
【典例1】(教材再开发·P93T5拓展)(2024·深圳福田期中)已知△ABC的三边长为a,b,c,且a,b,c都是整数.
(1)若a=2,b=5,且c为偶数.求△ABC的周长.
(2)化简:|a-b+c|-|b-c-a|+|a+b+c|.
【自主解答】(1)因为a=2,b=5,
所以5-2
当c=4时,△ABC的周长为a+b+c=2+5+4=11;
当c=6时,△ABC的周长为a+b+c=2+5+6=13,
综上所述,△ABC的周长为11或13.
(2)因为△ABC的边长为a,b,c,所以a+c>b,
所以|a-b+c|-|b-c-a|+|a+b+c|
=a+c-b-(a+c-b)+a+b+c
=a+c-b-a-c+b+a+b+c
=a+b+c.
1.(2024·广州越秀质检)下列长度的三条线段,能组成三角形的是( )
A.5,3,8 B.4,3,5
C.2,4,6 D.3,6,9
【解析】因为8=5+3,与两边之和大于第三边不一致,所以A不符合题意;
因为4+3=7>5,与两边之和大于第三边一致,
所以B符合题意;
因为4+2=6,不能组成三角形,
所以C不符合题意;
因为3+6=9,不能组成三角形,所以D不符合题意.
B
2.(2024·韶关模拟)如图所示,人字梯的支架AB,AC的长度都为2 m(连接处的长度忽略
不计),则B,C两点之间的距离可能是( )
A.3 m B.4.2 m
C.5 m D.6 m
A
【解析】因为AC=AB=2 m,
所以2-2
中的一根小棒用剪刀按图中所示的位置剪成两段,这两段小棒再与另一根小棒首尾
相接,能够围成一个三角形的是( )
B
【解析】A.图中小棒被剪刀剪成两段,这两段加起来比下面那根木棒短,不符合三角形的三边关系,无法围成三角形;
B.图中小棒被剪刀剪成两段,这两段加起来比上面那根木棒长,这两段相减比上面那根木棒短,符合三角形的三边关系,可以围成三角形;
C.图中小棒被剪刀剪成两段,这两段相减比下面那根木棒还长,不符合三角形的三边关系,无法围成三角形;
D.图中小棒被剪刀剪成两段,这两段加起来和上面那根木棒相等,不符合三角形的三边关系,无法围成三角形.
等腰三角形
【典例2】(教材再开发·P88“思考·交流”强化)已知x,y满足|4-x|+|y-6|=0,则以x,y的值为两边长的等腰三角形的周长是( )
A.14或16 B.14
C.16 D.以上答案均不对
【自主解答】选A.根据题意得,4-x=0,y-6=0,解得x=4,y=6,
①4是腰长时,三角形的三边长分别为4,4,6,
因为4+4=8,
所以三角形的周长为14;
②4是底边时,三角形的三边长分别为4,6,6,
能组成三角形,周长为4+6+6=16,
所以三角形的周长为14或16.
1.等腰三角形的周长为16,其中腰长为x,则x不可能为( )
A.4 B.5 C.6 D.7
A
【解析】A.当x=4时,三边长分别为4,4,8,
因为4+4=8,
所以不能围成三角形,
所以腰长不能为4,故该选项符合题意;
B.当x=5时,三边长分别为5,5,6,
因为5+5>6,
所以能围成三角形,
所以腰长能为5,故该选项不符合题意;
C.当x=6时,三边长分别为6,6,4,
因为4+6>6,
所以能围成三角形,
所以腰长能为6,故该选项不符合题意;
D.当x=7时,三边长分别为7,7,2,
因为7+2>7,
所以能围成三角形,
所以腰长能为7,故该选项不符合题意.
2.等腰三角形的一边等于3,一边等于6,则它的周长等于_______.
15
【解析】当3为腰,6为底时,3+3=6,不能构成等腰三角形;
当6为腰,3为底时,3+6>6,能构成等腰三角形,周长为3+6+6=15.
1.(2024·揭阳惠来期末)以下列长度的各组线段为边,能组成三角形的是( )
A.3 cm,7 cm,4 cm B.2 cm,3 cm,6 cm
C.5 cm,6 cm,7 cm D.1 cm,2 cm,3 cm
C
【解析】A.3+4=7,不能组成三角形,不符合题意;
B.2+3<6,不能组成三角形,不符合题意;
C.5+6>7,能组成三角形,符合题意;
D.1+2=3,不能组成三角形,不符合题意.
2.小明有两根长3 cm,7 cm的木棒,他想以这两根木棒为边做一个等腰三角形,还需再
选用一根长______cm的木棒.
7
【解析】当3 cm为腰长时,因为3+3=6<7,不符合三角形的三边关系,所以舍去;
当7 cm为腰长时,符合三角形的三边关系,符合题意.所以再选用一根长7 cm的木棒.
3.已知△ABC的三边长是a,b,c.
(1)若a=6,b=8,且三角形的周长是小于22的偶数,求c的值.
(2)化简|a+b-c|+|c-a-b|.
【解析】(1)因为a,b,c是△ABC的三边,a=6,b=8,所以2
知识点1 三角形按边分类
1.下列分类正确的是( )
A.三角形可分为等腰三角形、等边三角形
B.三角形可分为三边各不相等的三角形、等腰三角形以及等边三角形
C.三角形可分为三边各不相等的三角形和等边三角形
D.三角形可分为三边各不相等的三角形和等腰三角形
D
【解析】三角形可分为三边各不相等的三角形和等腰三角形.
2.设a,b,c分别是△ABC的三边长,且(a+b-c)(a-b)=0,则△ABC的形状是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰三角形
D
【解析】因为(a+b-c)(a-b)=0,
a+b>c,所以a+b-c>0,所以a-b=0,
所以a=b,所以△ABC为等腰三角形.
知识点2 三角形的三边关系
3.(2024·东莞期末)下列长度的各组线段中,能构成三角形的是( )
A.2,5,8 B.3,3,6 C.4,4,7 D.4,5,9
C
【解析】三角形的三边关系定理:任意两边之和大于第三边.
A.2+5=7<8,不能构成三角形,此项不符题意;
B.3+3=6,不能构成三角形,此项不符题意;
C.4+4>7,能构成三角形,此项符合题意;
D.4+5=9,不能构成三角形,此项不符题意.
4.(2024·深圳福田期中)已知三角形两边长分别为6和3,第三边的长是整数,这个三角
形周长的最小值是_______.
13
【解析】设第三边长为a,所以3
所以最小整数为4,
所以周长最小为6+4+3=13.
5.(2023·河北中考)四边形ABCD的边长如图所示,对角线AC的长度随四边形形状的改
变而变化.当△ABC为等腰三角形时,对角线AC的长为( )
A.2 B.3 C.4 D.5
B
【解析】因为△ABC为等腰三角形,
所以AB=AC或AC=BC,
当AC=BC=4时,AD+CD=AC=4,此时不满足三角形三边关系定理,
当AC=AB=3时,满足三角形三边关系定理,
所以AC=3.
6.(2024·佛山禅城区期末)如图所示,△ABC被木板遮住了一部分,其中AB=5,则AC+BC
的值可能是( )
A.3 B.4 C.5 D.6
D
【解析】因为三角形两边之和大于第三边,
所以AC+BC>AB,
因为AB=5,所以AC+BC>5.
7.(2024·深圳南山区期中)设a,b,c为△ABC的三边,化简|a-b+c|-|a+b-c|-|a-b-c|=
___________.
a-3b+c
【解析】因为a,b,c为△ABC的三边,
所以a+c>b,a+b>c,b+c>a,
所以a-b+c>0,a+b-c>0,a-b-c<0,
所以|a-b+c|-|a+b-c|-|a-b-c|=a-b+c-(a+b-c)+(a-b-c)=a-b+c-a-b+c+a-b-c=a-3b+c.
8.已知a,b,c是△ABC的三边长,且a,b,c都是整数.
(1)若a,b,c满足|a-b|+|b-c|=0,试判断△ABC的形状.
(2)若a=2,b=5,且c是奇数,试判断△ABC的形状.
【解析】(1)因为a,b,c满足|a-b|+|b-c|=0,所以a-b=0,b-c=0,
所以a=b=c,
所以△ABC的形状是等边三角形.
(2)因为a=2,b=5,所以5-2
所以c=5,所以b=c,
所以△ABC的形状是等腰三角形.
同课章节目录
