4.1.3 认识三角形 第3课时 课件(共29张PPT)
文档属性
| 名称 | 4.1.3 认识三角形 第3课时 课件(共29张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 17:06:31 | ||
图片预览







文档简介
(共29张PPT)
1 认识三角形
第3课时
课时目标 素养达成
了解三角形的角平分线、高、中线,并能在具体的三角形中作出它们 空间观念、几何直观、
推理能力
如图所示,(1)若AM是△ABC的中线,BC=12 cm,则BM=CM=______cm.
(2)若AD是△ABC的角平分线,则∠BAD=∠DAC=__________.
(3)若AH是△ABC的高,则△ABH是_________三角形.
6
直角
三角形三条重要线段的画法及辨识
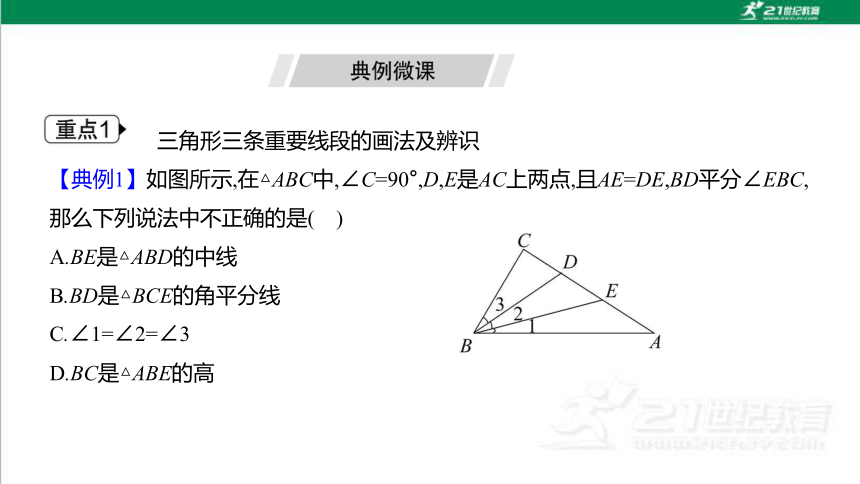
【典例1】如图所示,在△ABC中,∠C=90°,D,E是AC上两点,且AE=DE,BD平分∠EBC,那么下列说法中不正确的是( )
A.BE是△ABD的中线
B.BD是△BCE的角平分线
C.∠1=∠2=∠3
D.BC是△ABE的高
【自主解答】选C.A.因为AE=DE,所以BE是△ABD的中线,正确,不符合题意;
B.因为BD平分∠EBC,所以BD是△EBC的角平分线,正确,不符合题意;
C.因为BD是△EBC的角平分线,所以∠EBD=∠CBD,因为BE不是△ABD的角平分线,所以无法得出∠EBD=∠ABE,所以∠1=∠2=∠3不正确,符合题意;
D.因为∠C=90°,所以BC是△ABE的高,正确,不符合题意.
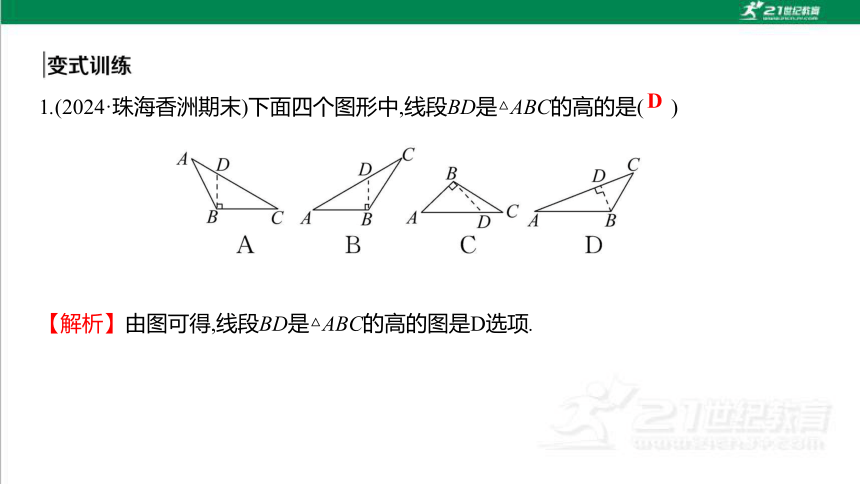
1.(2024·珠海香洲期末)下面四个图形中,线段BD是△ABC的高的是( )
D
【解析】由图可得,线段BD是△ABC的高的图是D选项.
D
三角形三条重要线段的作用
【典例2】
如图所示,△ABC中,AB=6 cm,BC=10 cm,CE⊥AB,AD⊥BC,AD和CE交于点F.
(1)若∠B=55°,求∠AFC的度数;
(2)若AD=4 cm,求CE的长.
1.(2024·广州海珠期末)如图所示,CM是△ABC的中线,BC=8 cm,若△BCM的周长比
△ACM的周长大2 cm,则AC的长为( )
A.3 cm B.4 cm C.5 cm D.6 cm
D
【解析】因为CM是△ABC的中线,BC=8 cm,
所以AM=BM,
所以△BCM的周长为BC+BM+CM,△ACM的周长为AC+AM+CM,
因为△BCM的周长比△ACM的周长大2 cm,
所以BC+BM+CM-(AC+AM+CM)=2,
即BC-AC=2,
所以8-AC=2,解得AC=6 cm.
2.(2024·汕头潮南期末)如图所示,BD是△ABC的中线,若△ABD的
面积是10,则△ABC的面积是_______.
20
【解析】因为BD是△ABC的中线,
所以S△ABD=S△BCD,
因为△ABD的面积是10,
所以S△ABC=10+10=20.
1.(2024·河源龙川期末)如图所示,在△ABC中,边AB上的高是( )
A.AF B.BE C.CE D.BD
C
【解析】△ABC中,过点C作边AB的垂线,与直线AB相交,点C与交点之间的线段是边AB上的高,由题图可知,CE是边AB上的高.
2.如图所示,△ABC的角平分线AD、中线BE相交于点O.有下列两个结论:①AO是
△ABE的角平分线;②BO是△ABD的中线.其中( )
A.只有①正确 B.只有②正确
C.①和②都正确 D.①和②都不正确
A
【解析】AD是△ABC的角平分线,则是∠BAC的平分线,所以AO是△ABE的角平分线,故①正确;BE是△ABC的中线,则E是AC的中点,而O一定不是AD的中点,故②错误.
3.如图所示,在△ABC中BE是角平分线,点D在边AB上(不与点A,B重合),CD与BE交于点O.
(1)若CD是△ABC的中线,BC=4,AC=3,则△BCD与△ACD的周长差为 .
(2)若∠ABC=64°,CD是△ABC的高,求∠BOC的度数.
(3)若∠A=80°,CD是△ABC的角平分线,求∠BOC的度数.
【解析】(1)因为CD是△ABC的中线,
所以BD=AD,
因为BC=4,AC=3,
所以C△BCD=BC+BD+CD=4+AD+CD,C△ACD=AD+CD+AC=3+AD+CD,
所以C△BCD-C△ACD=1.
答案:1
知识点1 三角形的高
1.(2024·深圳宝安期中)在△ABC中,作出AC边上的高,正确的是( )
D
【解析】根据三角形高线的定义,AC边上的高是过点B向AC作垂线,垂足为D,
纵观各图形,D选项符合高线的定义.
2.如图所示:
(1)在△ABC中,BC边上的高是________.
(2)在△AEC中,AE边上的高是________.
(3)在△FEC中,EC边上的高是________.
(4)若AB=CD=2 cm,AE=3 cm,则S△AEC=______cm2,CE=______cm.
AB
CD
FE
3
3
知识点2 三角形的中线
3.在△ABC中,点D在边BC上,线段AD将△ABC分成两个面积相等的三角形,线段AD是
△ABC的_________.
中线
4.如图所示,已知AD为△ABC的中线,AB=10 cm,AC=7 cm,△ACD的周长为20 cm,则
△ABD的周长为_______cm.
23
【解析】因为AD是BC边上的中线,
所以BD=CD,
所以△ABD和△ACD周长的差为(AB+BD+AD)-(AC+AD+CD)=AB-AC=10-7=
3(cm),
因为△ACD的周长为20 cm,AB比AC长3 cm,
所以△ABD周长为20+3=23(cm).
C
6.如图所示,在△ABC中,AD是高,AE是角平分线,AF是中线,则下列说法中,错误的是( )
A.BF=CF B.∠C+∠CAD=90°
C.∠BAF=∠CAF D.S△ABC=2S△ABF
C
【解析】因为AF是△ABC的中线,
所以BF=CF,A说法正确,不符合题意;
因为AD是高,所以∠ADC=90°,
所以∠C+∠CAD=90°,B说法正确,不符合题意;因为AE是角平分线,
所以∠BAE=∠CAE,而∠BAF与∠CAF不一定相等,C说法错误,符合题意;
因为BF=CF,所以S△ABC=2S△ABF,D说法正确,不符合题意.
D
8.(2024·深圳南山期末)如图所示,△ABC中,AD,AE分别为角平分线和高,∠B=46°,
∠C=64°,则∠DAE=_______.
9°
9.(2024·佛山顺德质检)如图所示,在△ABC中,∠ABC和∠ACB的平分线相交于点P,若
∠BPC=148°,则∠A的度数为_________.
116°
【解析】因为∠BPC=148°,
所以∠PCB+∠PBC=180°-∠BPC=180°-148°=32°,
因为BD平分∠ABC,CE平分∠ACB,
所以∠ABC=2∠PBC,∠ACB=2∠PCB,
所以∠ACB+∠ABC=2(∠PCB+∠PBC)=2×32°=64°,
所以∠A=180°-(∠ACB+∠ABC)=180°-64°=116°.
10.已知△ABC(如图所示).
(1)作△ABC的中线AD.
(2)作△ABD的角平分线DM.
(3)作△ACD的高CN.
(4)若C△ADC-C△ADB=3(C表示周长),且AB=4,则AC= .
【解析】(1)如图所示,AD为所作.
(2)如图所示,DM为所作.
(3)如图所示,CN为所作.
(4)因为AD为△ABC的中线,
所以BD=CD,
因为C△ADC-C△ADB=3,
所以AC+AD+CD-(AB+AD+BD)=3,
所以AC-AB=3,
因为AB=4,所以AC=AB+3=4+3=7.
答案:7
1 认识三角形
第3课时
课时目标 素养达成
了解三角形的角平分线、高、中线,并能在具体的三角形中作出它们 空间观念、几何直观、
推理能力
如图所示,(1)若AM是△ABC的中线,BC=12 cm,则BM=CM=______cm.
(2)若AD是△ABC的角平分线,则∠BAD=∠DAC=__________.
(3)若AH是△ABC的高,则△ABH是_________三角形.
6
直角
三角形三条重要线段的画法及辨识
【典例1】如图所示,在△ABC中,∠C=90°,D,E是AC上两点,且AE=DE,BD平分∠EBC,那么下列说法中不正确的是( )
A.BE是△ABD的中线
B.BD是△BCE的角平分线
C.∠1=∠2=∠3
D.BC是△ABE的高
【自主解答】选C.A.因为AE=DE,所以BE是△ABD的中线,正确,不符合题意;
B.因为BD平分∠EBC,所以BD是△EBC的角平分线,正确,不符合题意;
C.因为BD是△EBC的角平分线,所以∠EBD=∠CBD,因为BE不是△ABD的角平分线,所以无法得出∠EBD=∠ABE,所以∠1=∠2=∠3不正确,符合题意;
D.因为∠C=90°,所以BC是△ABE的高,正确,不符合题意.
1.(2024·珠海香洲期末)下面四个图形中,线段BD是△ABC的高的是( )
D
【解析】由图可得,线段BD是△ABC的高的图是D选项.
D
三角形三条重要线段的作用
【典例2】
如图所示,△ABC中,AB=6 cm,BC=10 cm,CE⊥AB,AD⊥BC,AD和CE交于点F.
(1)若∠B=55°,求∠AFC的度数;
(2)若AD=4 cm,求CE的长.
1.(2024·广州海珠期末)如图所示,CM是△ABC的中线,BC=8 cm,若△BCM的周长比
△ACM的周长大2 cm,则AC的长为( )
A.3 cm B.4 cm C.5 cm D.6 cm
D
【解析】因为CM是△ABC的中线,BC=8 cm,
所以AM=BM,
所以△BCM的周长为BC+BM+CM,△ACM的周长为AC+AM+CM,
因为△BCM的周长比△ACM的周长大2 cm,
所以BC+BM+CM-(AC+AM+CM)=2,
即BC-AC=2,
所以8-AC=2,解得AC=6 cm.
2.(2024·汕头潮南期末)如图所示,BD是△ABC的中线,若△ABD的
面积是10,则△ABC的面积是_______.
20
【解析】因为BD是△ABC的中线,
所以S△ABD=S△BCD,
因为△ABD的面积是10,
所以S△ABC=10+10=20.
1.(2024·河源龙川期末)如图所示,在△ABC中,边AB上的高是( )
A.AF B.BE C.CE D.BD
C
【解析】△ABC中,过点C作边AB的垂线,与直线AB相交,点C与交点之间的线段是边AB上的高,由题图可知,CE是边AB上的高.
2.如图所示,△ABC的角平分线AD、中线BE相交于点O.有下列两个结论:①AO是
△ABE的角平分线;②BO是△ABD的中线.其中( )
A.只有①正确 B.只有②正确
C.①和②都正确 D.①和②都不正确
A
【解析】AD是△ABC的角平分线,则是∠BAC的平分线,所以AO是△ABE的角平分线,故①正确;BE是△ABC的中线,则E是AC的中点,而O一定不是AD的中点,故②错误.
3.如图所示,在△ABC中BE是角平分线,点D在边AB上(不与点A,B重合),CD与BE交于点O.
(1)若CD是△ABC的中线,BC=4,AC=3,则△BCD与△ACD的周长差为 .
(2)若∠ABC=64°,CD是△ABC的高,求∠BOC的度数.
(3)若∠A=80°,CD是△ABC的角平分线,求∠BOC的度数.
【解析】(1)因为CD是△ABC的中线,
所以BD=AD,
因为BC=4,AC=3,
所以C△BCD=BC+BD+CD=4+AD+CD,C△ACD=AD+CD+AC=3+AD+CD,
所以C△BCD-C△ACD=1.
答案:1
知识点1 三角形的高
1.(2024·深圳宝安期中)在△ABC中,作出AC边上的高,正确的是( )
D
【解析】根据三角形高线的定义,AC边上的高是过点B向AC作垂线,垂足为D,
纵观各图形,D选项符合高线的定义.
2.如图所示:
(1)在△ABC中,BC边上的高是________.
(2)在△AEC中,AE边上的高是________.
(3)在△FEC中,EC边上的高是________.
(4)若AB=CD=2 cm,AE=3 cm,则S△AEC=______cm2,CE=______cm.
AB
CD
FE
3
3
知识点2 三角形的中线
3.在△ABC中,点D在边BC上,线段AD将△ABC分成两个面积相等的三角形,线段AD是
△ABC的_________.
中线
4.如图所示,已知AD为△ABC的中线,AB=10 cm,AC=7 cm,△ACD的周长为20 cm,则
△ABD的周长为_______cm.
23
【解析】因为AD是BC边上的中线,
所以BD=CD,
所以△ABD和△ACD周长的差为(AB+BD+AD)-(AC+AD+CD)=AB-AC=10-7=
3(cm),
因为△ACD的周长为20 cm,AB比AC长3 cm,
所以△ABD周长为20+3=23(cm).
C
6.如图所示,在△ABC中,AD是高,AE是角平分线,AF是中线,则下列说法中,错误的是( )
A.BF=CF B.∠C+∠CAD=90°
C.∠BAF=∠CAF D.S△ABC=2S△ABF
C
【解析】因为AF是△ABC的中线,
所以BF=CF,A说法正确,不符合题意;
因为AD是高,所以∠ADC=90°,
所以∠C+∠CAD=90°,B说法正确,不符合题意;因为AE是角平分线,
所以∠BAE=∠CAE,而∠BAF与∠CAF不一定相等,C说法错误,符合题意;
因为BF=CF,所以S△ABC=2S△ABF,D说法正确,不符合题意.
D
8.(2024·深圳南山期末)如图所示,△ABC中,AD,AE分别为角平分线和高,∠B=46°,
∠C=64°,则∠DAE=_______.
9°
9.(2024·佛山顺德质检)如图所示,在△ABC中,∠ABC和∠ACB的平分线相交于点P,若
∠BPC=148°,则∠A的度数为_________.
116°
【解析】因为∠BPC=148°,
所以∠PCB+∠PBC=180°-∠BPC=180°-148°=32°,
因为BD平分∠ABC,CE平分∠ACB,
所以∠ABC=2∠PBC,∠ACB=2∠PCB,
所以∠ACB+∠ABC=2(∠PCB+∠PBC)=2×32°=64°,
所以∠A=180°-(∠ACB+∠ABC)=180°-64°=116°.
10.已知△ABC(如图所示).
(1)作△ABC的中线AD.
(2)作△ABD的角平分线DM.
(3)作△ACD的高CN.
(4)若C△ADC-C△ADB=3(C表示周长),且AB=4,则AC= .
【解析】(1)如图所示,AD为所作.
(2)如图所示,DM为所作.
(3)如图所示,CN为所作.
(4)因为AD为△ABC的中线,
所以BD=CD,
因为C△ADC-C△ADB=3,
所以AC+AD+CD-(AB+AD+BD)=3,
所以AC-AB=3,
因为AB=4,所以AC=AB+3=4+3=7.
答案:7
同课章节目录
