5.1轴对称及其性质 课件(共29张PPT)
文档属性
| 名称 | 5.1轴对称及其性质 课件(共29张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 885.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 17:05:02 | ||
图片预览







文档简介
(共29张PPT)
1 轴对称及其性质
课时目标 素养达成
1.理解轴对称图形和成轴对称的图形的意义,能够识别这些图形并找出它们的对称轴 几何直观、空间观念
2.探索轴对称性质,理解对应点所连的线段被对称轴垂直平分,对应线段相等,对应角相等的性质 空间观念、推理能力
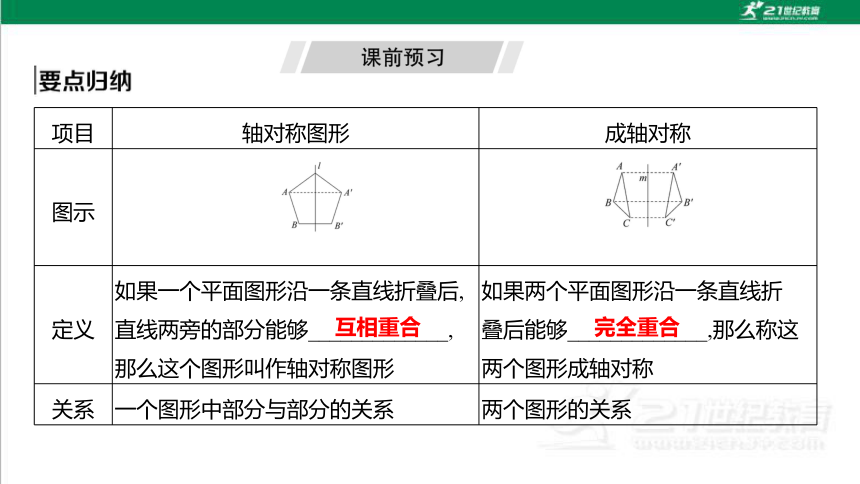
项目 轴对称图形 成轴对称
图示
定义 如果一个平面图形沿一条直线折叠后,
直线两旁的部分能够_____________,
那么这个图形叫作轴对称图形 如果两个平面图形沿一条直线折
叠后能够_____________,那么称这
两个图形成轴对称
关系 一个图形中部分与部分的关系 两个图形的关系
互相重合
完全重合
项目 轴对称图形 成轴对称
对应
线段 AB=__________ AB=__________
BC=__________
AC=A'C'
对应角 ∠A=∠A'
∠B=∠B' ∠A=∠A'
∠B=∠B'
∠C=∠C'
对称轴位置 垂直平分AA',BB' 垂直平分AA',BB',CC'
性质 对应点所连的线段被对称轴_____________,对应线段_________,
对应角_________
A'B'
A'B'
B'C'
垂直平分
相等
相等
1.现实世界中,对称现象无处不在,中国的方块字中有些也具有对称性.下列汉字中,是
轴对称图形的是( )
C
2.如图所示,是轴对称图形且只有两条对称轴的是_________.(填序号)
①②
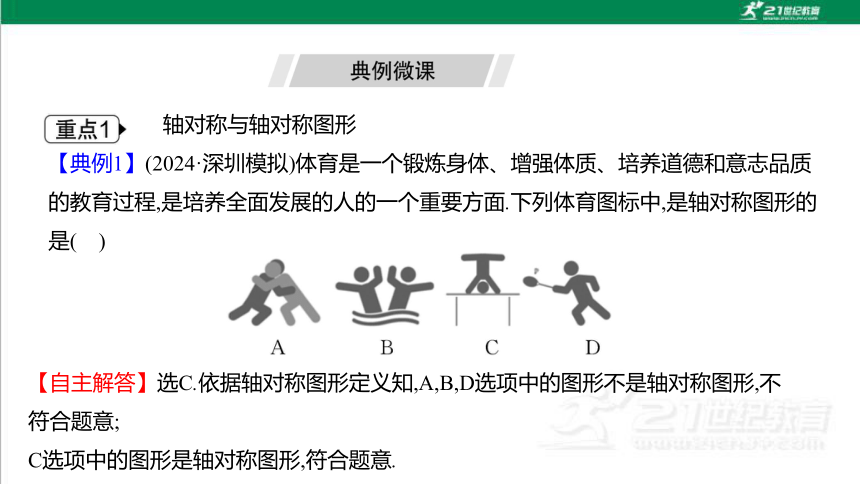
轴对称与轴对称图形
【典例1】(2024·深圳模拟)体育是一个锻炼身体、增强体质、培养道德和意志品质的教育过程,是培养全面发展的人的一个重要方面.下列体育图标中,是轴对称图形的是( )
【自主解答】选C.依据轴对称图形定义知,A,B,D选项中的图形不是轴对称图形,不符合题意;
C选项中的图形是轴对称图形,符合题意.
(2024·惠州惠阳三模)“书法”是我国汉字特有的一种传统艺术,它是我国十大国粹之
一.下面的“美”字分别采用楷书、行书、草书、篆书等四种不同字体书写而成,它们
呈现出美的不同形态.其中符合轴对称美的是( )
D
【解析】选项A,B,C的“美”字不能找到一条直线,使图形沿一条直线折叠后,直线两旁的部分能够互相重合,所以不是轴对称图形.
选项D的“美”字能找到一条直线,使图形沿一条直线折叠后,直线两旁的部分能够互相重合,所以是轴对称图形.
轴对称的性质
【典例2】(教材再开发·P126T3强化)
(2024·河北中考)如图所示,AD与BC交于点O,△ABO和△CDO关于直线PQ对称,点A,B的对称点分别是点C,D.下列选项中,不一定正确的是( )
A.AD⊥BC B.AC⊥PQ
C.△ABO≌△CDO D.AC∥BD
【自主解答】选A.如图所示,连接AC,BD,
因为△ABO和△CDO关于直线PQ对称,所以△ABO≌△CDO,PQ⊥AC,PQ⊥BD,
所以AC∥BD,故B,C,D选项正确.
AD不一定垂直BC,故A选项不一定正确.
如图所示,四边形ABCD与四边形EFGH关于MN对称.
(1)A,B,C,D的对应点分别是 ,线段AD,AB的对应线段分别是 ,
CD= ,∠CBA= ,∠ADC= .
(2)连接AE,BF,AE与BF平行吗 为什么
(3)写出对称轴MN与线段AE的关系.
【解析】(1)A,B,C,D的对应点分别是E,F,G,H,线段AD,AB的对应线段分别是EH,EF,CD=GH,∠CBA=∠GFE,∠ADC=∠EHG.
答案:E,F,G,H EH,EF GH ∠GFE ∠EHG
(2)AE∥BF.对应点的连线互相平行或共线,这里不共线,所以平行.
(3)对称轴MN垂直平分AE.依据是对称轴垂直平分对应点所连的线段.
1.在以下四个标志中,是轴对称图形的是( )
D
【解析】选项A,B,C不能找到这样的一条直线,使图形沿一条直线折叠后,直线两旁的部分能够互相重合,所以不是轴对称图形.选项D能找到这样的一条直线,使图形沿一条直线折叠后,直线两旁的部分能够互相重合,所以是轴对称图形.
2.(2024·广州白云质检)如图所示,△ABC与△A'B'C'关于直线l对称,
则∠B的度数为( )
A.100° B.90°
C.50° D.30°
A
【解析】因为△ABC与△A'B'C'关于直线l对称,∠C'=30°,∠A=50°,
所以∠C=∠C'=30°.
所以∠B=180°-∠A-∠C=180°-50°-30°=100°.
知识点1 轴对称与轴对称图形
1.(2024·深圳宝安模拟)下列几种著名的数学曲线中,不是轴对称图形的是( )
A
【解析】A.不是轴对称图形,故此选项符合题意;
B.是轴对称图形,故此选项不符合题意;
C.是轴对称图形,故此选项不符合题意;
D.是轴对称图形,故此选项不符合题意.
2.(2024·肇庆高要二模)下列关于体育运动的图标中,是轴对称图形的为( )
A
【解析】选项B,C,D不能找到这样的一条直线,使图形沿这条直线折叠后,直线两旁的部分能够互相重合,所以不是轴对称图形.选项A能找到一条直线,使图形沿这条直线折叠后,直线两旁的部分能够互相重合,所以是轴对称图形.
知识点2 轴对称的性质
3.(2024·惠州惠城期中)如图所示,若△ABC与△A1B1C1关于直线MN对称,BB1交MN于点
O,则下列说法中,不一定正确的是( )
A.AC=A1C1 B.BO=B1O
C.CC1⊥MN D.AB∥B1C1
D
【解析】因为△ABC与△A1B1C1关于直线MN对称,
所以AC=A1C1,BO=B1O,CC1⊥MN,
故选项A,B,C正确,不符合题意;
AB∥B1C1不一定成立,
故选项D错误,符合题意.
4.(2024·揭阳揭西期末)如图所示,△ABC与△A'B'C'关于直线l对称,且∠A=78°,∠C'=48°,
则∠B的度数为_______°.
54
【解析】因为△ABC与△A'B'C'关于直线l对称,且∠A=78°,∠C'=48°,所以∠B=180°-78°-48°=54°.
5.汉字是世界上最古老的文字之一,现存最早的汉字是公元前14世纪殷商时期的甲
骨文,之后又产生了金文、小篆、隶书、草书、楷书、行书等多种字体,每种字体都
有着鲜明的艺术特征.下面的汉字可以近似地看成轴对称图形的是( )
B
【解析】选项A,C,D中的图形不能找到这样的一条直线,使图形沿一条直线折叠后,直线两旁的部分互相重合,所以不是轴对称图形;B选项中的图形能找到这样的一条直线,使图形沿一条直线折叠后,直线两旁的部分互相重合,所以是轴对称图形.
6.如图所示,四边形ABCD是轴对称图形,直线AC是它的对称轴,若∠BAC=65°,∠B=
50°,则∠BCD的大小为_________.
130°
【解析】因为四边形ABCD是轴对称图形,直线AC是它的对称轴,
所以∠DAC=∠BAC=65°,∠D=∠B=50°,
所以∠BCA=∠DCA=180°-65°-50°=65°,
所以∠BCD的大小为65°×2=130°.
7.如图所示,点P为∠AOB内任一点,E,F分别为点P关于OA,OB的对称点.若∠AOB=30°,
则∠E+∠F=_________.
150°
【解析】连接OP.
因为E,F分别为点P关于OA,OB的对称点,
所以∠EOA=∠AOP,∠POB=∠BOF.
因为∠AOB=∠AOP+∠POB,
所以∠EOF=2∠AOB=60°.
因为E,F分别为点P关于OA,OB的对称点,
所以PE⊥OA,PF⊥OB.
因为∠AOB=30°,所以∠EPF=150°,
所以∠E+∠F=360°-60°-150°=150°.
8.如图所示,点P在∠AOB的内部,点C和点P关于OA对称,点P关于OB的对称点是点D,连接CD交OA于点M,交OB于点N.
(1)①若∠AOB=70°,则∠COD= .
②若∠AOB=α,求∠COD的度数.
(2)若CD=8,求△PMN的周长.
【解析】(1)①因为点C和点P关于OA对称,
所以∠AOC=∠AOP.
因为点P关于OB的对称点是点D,
所以∠BOD=∠BOP.所以∠COD=∠AOC+∠AOP+∠BOP+∠BOD=2(∠AOP+∠BOP)=2∠AOB=2×70°=140°.
答案:140°
②因为点C和点P关于OA对称.
所以∠AOC=∠AOP.
因为点P关于OB的对称点是点D,所以∠BOD=∠BOP.
所以∠COD=∠AOC+∠AOP+∠BOP+∠BOD=2(∠AOP+∠BOP)=2∠AOB=2α.
(2)根据轴对称的性质,
可知CM=PM,DN=PN,
所以△PMN的周长为PM+PN+MN=CM+DN+MN=CD=8.
9.(2024·梅州大埔期末)如图所示,在正方形网格上有一个△ABC.
(1)画出△ABC关于直线MN的对称图形(不写画法).
(2)若网格上的每个小正方形的边长为1,则△ABC的面积为 .
1 轴对称及其性质
课时目标 素养达成
1.理解轴对称图形和成轴对称的图形的意义,能够识别这些图形并找出它们的对称轴 几何直观、空间观念
2.探索轴对称性质,理解对应点所连的线段被对称轴垂直平分,对应线段相等,对应角相等的性质 空间观念、推理能力
项目 轴对称图形 成轴对称
图示
定义 如果一个平面图形沿一条直线折叠后,
直线两旁的部分能够_____________,
那么这个图形叫作轴对称图形 如果两个平面图形沿一条直线折
叠后能够_____________,那么称这
两个图形成轴对称
关系 一个图形中部分与部分的关系 两个图形的关系
互相重合
完全重合
项目 轴对称图形 成轴对称
对应
线段 AB=__________ AB=__________
BC=__________
AC=A'C'
对应角 ∠A=∠A'
∠B=∠B' ∠A=∠A'
∠B=∠B'
∠C=∠C'
对称轴位置 垂直平分AA',BB' 垂直平分AA',BB',CC'
性质 对应点所连的线段被对称轴_____________,对应线段_________,
对应角_________
A'B'
A'B'
B'C'
垂直平分
相等
相等
1.现实世界中,对称现象无处不在,中国的方块字中有些也具有对称性.下列汉字中,是
轴对称图形的是( )
C
2.如图所示,是轴对称图形且只有两条对称轴的是_________.(填序号)
①②
轴对称与轴对称图形
【典例1】(2024·深圳模拟)体育是一个锻炼身体、增强体质、培养道德和意志品质的教育过程,是培养全面发展的人的一个重要方面.下列体育图标中,是轴对称图形的是( )
【自主解答】选C.依据轴对称图形定义知,A,B,D选项中的图形不是轴对称图形,不符合题意;
C选项中的图形是轴对称图形,符合题意.
(2024·惠州惠阳三模)“书法”是我国汉字特有的一种传统艺术,它是我国十大国粹之
一.下面的“美”字分别采用楷书、行书、草书、篆书等四种不同字体书写而成,它们
呈现出美的不同形态.其中符合轴对称美的是( )
D
【解析】选项A,B,C的“美”字不能找到一条直线,使图形沿一条直线折叠后,直线两旁的部分能够互相重合,所以不是轴对称图形.
选项D的“美”字能找到一条直线,使图形沿一条直线折叠后,直线两旁的部分能够互相重合,所以是轴对称图形.
轴对称的性质
【典例2】(教材再开发·P126T3强化)
(2024·河北中考)如图所示,AD与BC交于点O,△ABO和△CDO关于直线PQ对称,点A,B的对称点分别是点C,D.下列选项中,不一定正确的是( )
A.AD⊥BC B.AC⊥PQ
C.△ABO≌△CDO D.AC∥BD
【自主解答】选A.如图所示,连接AC,BD,
因为△ABO和△CDO关于直线PQ对称,所以△ABO≌△CDO,PQ⊥AC,PQ⊥BD,
所以AC∥BD,故B,C,D选项正确.
AD不一定垂直BC,故A选项不一定正确.
如图所示,四边形ABCD与四边形EFGH关于MN对称.
(1)A,B,C,D的对应点分别是 ,线段AD,AB的对应线段分别是 ,
CD= ,∠CBA= ,∠ADC= .
(2)连接AE,BF,AE与BF平行吗 为什么
(3)写出对称轴MN与线段AE的关系.
【解析】(1)A,B,C,D的对应点分别是E,F,G,H,线段AD,AB的对应线段分别是EH,EF,CD=GH,∠CBA=∠GFE,∠ADC=∠EHG.
答案:E,F,G,H EH,EF GH ∠GFE ∠EHG
(2)AE∥BF.对应点的连线互相平行或共线,这里不共线,所以平行.
(3)对称轴MN垂直平分AE.依据是对称轴垂直平分对应点所连的线段.
1.在以下四个标志中,是轴对称图形的是( )
D
【解析】选项A,B,C不能找到这样的一条直线,使图形沿一条直线折叠后,直线两旁的部分能够互相重合,所以不是轴对称图形.选项D能找到这样的一条直线,使图形沿一条直线折叠后,直线两旁的部分能够互相重合,所以是轴对称图形.
2.(2024·广州白云质检)如图所示,△ABC与△A'B'C'关于直线l对称,
则∠B的度数为( )
A.100° B.90°
C.50° D.30°
A
【解析】因为△ABC与△A'B'C'关于直线l对称,∠C'=30°,∠A=50°,
所以∠C=∠C'=30°.
所以∠B=180°-∠A-∠C=180°-50°-30°=100°.
知识点1 轴对称与轴对称图形
1.(2024·深圳宝安模拟)下列几种著名的数学曲线中,不是轴对称图形的是( )
A
【解析】A.不是轴对称图形,故此选项符合题意;
B.是轴对称图形,故此选项不符合题意;
C.是轴对称图形,故此选项不符合题意;
D.是轴对称图形,故此选项不符合题意.
2.(2024·肇庆高要二模)下列关于体育运动的图标中,是轴对称图形的为( )
A
【解析】选项B,C,D不能找到这样的一条直线,使图形沿这条直线折叠后,直线两旁的部分能够互相重合,所以不是轴对称图形.选项A能找到一条直线,使图形沿这条直线折叠后,直线两旁的部分能够互相重合,所以是轴对称图形.
知识点2 轴对称的性质
3.(2024·惠州惠城期中)如图所示,若△ABC与△A1B1C1关于直线MN对称,BB1交MN于点
O,则下列说法中,不一定正确的是( )
A.AC=A1C1 B.BO=B1O
C.CC1⊥MN D.AB∥B1C1
D
【解析】因为△ABC与△A1B1C1关于直线MN对称,
所以AC=A1C1,BO=B1O,CC1⊥MN,
故选项A,B,C正确,不符合题意;
AB∥B1C1不一定成立,
故选项D错误,符合题意.
4.(2024·揭阳揭西期末)如图所示,△ABC与△A'B'C'关于直线l对称,且∠A=78°,∠C'=48°,
则∠B的度数为_______°.
54
【解析】因为△ABC与△A'B'C'关于直线l对称,且∠A=78°,∠C'=48°,所以∠B=180°-78°-48°=54°.
5.汉字是世界上最古老的文字之一,现存最早的汉字是公元前14世纪殷商时期的甲
骨文,之后又产生了金文、小篆、隶书、草书、楷书、行书等多种字体,每种字体都
有着鲜明的艺术特征.下面的汉字可以近似地看成轴对称图形的是( )
B
【解析】选项A,C,D中的图形不能找到这样的一条直线,使图形沿一条直线折叠后,直线两旁的部分互相重合,所以不是轴对称图形;B选项中的图形能找到这样的一条直线,使图形沿一条直线折叠后,直线两旁的部分互相重合,所以是轴对称图形.
6.如图所示,四边形ABCD是轴对称图形,直线AC是它的对称轴,若∠BAC=65°,∠B=
50°,则∠BCD的大小为_________.
130°
【解析】因为四边形ABCD是轴对称图形,直线AC是它的对称轴,
所以∠DAC=∠BAC=65°,∠D=∠B=50°,
所以∠BCA=∠DCA=180°-65°-50°=65°,
所以∠BCD的大小为65°×2=130°.
7.如图所示,点P为∠AOB内任一点,E,F分别为点P关于OA,OB的对称点.若∠AOB=30°,
则∠E+∠F=_________.
150°
【解析】连接OP.
因为E,F分别为点P关于OA,OB的对称点,
所以∠EOA=∠AOP,∠POB=∠BOF.
因为∠AOB=∠AOP+∠POB,
所以∠EOF=2∠AOB=60°.
因为E,F分别为点P关于OA,OB的对称点,
所以PE⊥OA,PF⊥OB.
因为∠AOB=30°,所以∠EPF=150°,
所以∠E+∠F=360°-60°-150°=150°.
8.如图所示,点P在∠AOB的内部,点C和点P关于OA对称,点P关于OB的对称点是点D,连接CD交OA于点M,交OB于点N.
(1)①若∠AOB=70°,则∠COD= .
②若∠AOB=α,求∠COD的度数.
(2)若CD=8,求△PMN的周长.
【解析】(1)①因为点C和点P关于OA对称,
所以∠AOC=∠AOP.
因为点P关于OB的对称点是点D,
所以∠BOD=∠BOP.所以∠COD=∠AOC+∠AOP+∠BOP+∠BOD=2(∠AOP+∠BOP)=2∠AOB=2×70°=140°.
答案:140°
②因为点C和点P关于OA对称.
所以∠AOC=∠AOP.
因为点P关于OB的对称点是点D,所以∠BOD=∠BOP.
所以∠COD=∠AOC+∠AOP+∠BOP+∠BOD=2(∠AOP+∠BOP)=2∠AOB=2α.
(2)根据轴对称的性质,
可知CM=PM,DN=PN,
所以△PMN的周长为PM+PN+MN=CM+DN+MN=CD=8.
9.(2024·梅州大埔期末)如图所示,在正方形网格上有一个△ABC.
(1)画出△ABC关于直线MN的对称图形(不写画法).
(2)若网格上的每个小正方形的边长为1,则△ABC的面积为 .
同课章节目录
