5.2.1简单的轴对称图形第1课时 课件(共30张PPT)
文档属性
| 名称 | 5.2.1简单的轴对称图形第1课时 课件(共30张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 16:58:16 | ||
图片预览








文档简介
(共30张PPT)
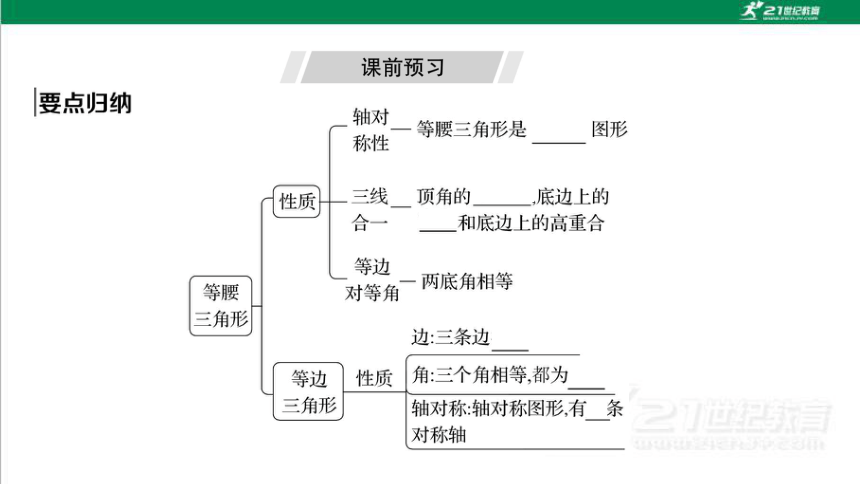
2 简单的轴对称图形
第1课时
课时目标 素养达成
1.探索并了解等腰三角形的轴对称性及其相关性质 推理能力、几何直观
2.经历探索简单图形的轴对称性的过程,进一步理解轴对称的性质,积累数学活动经验 空间观念
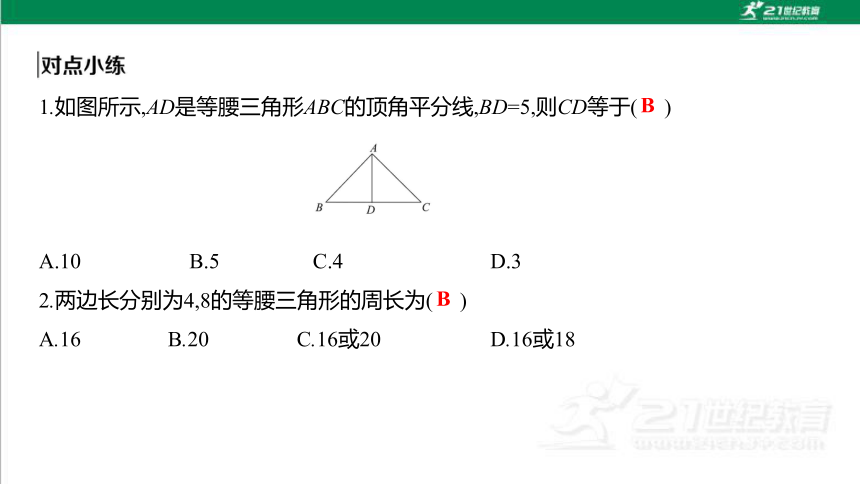
1.如图所示,AD是等腰三角形ABC的顶角平分线,BD=5,则CD等于( )
A.10 B.5 C.4 D.3
2.两边长分别为4,8的等腰三角形的周长为( )
A.16 B.20 C.16或20 D.16或18
B
B
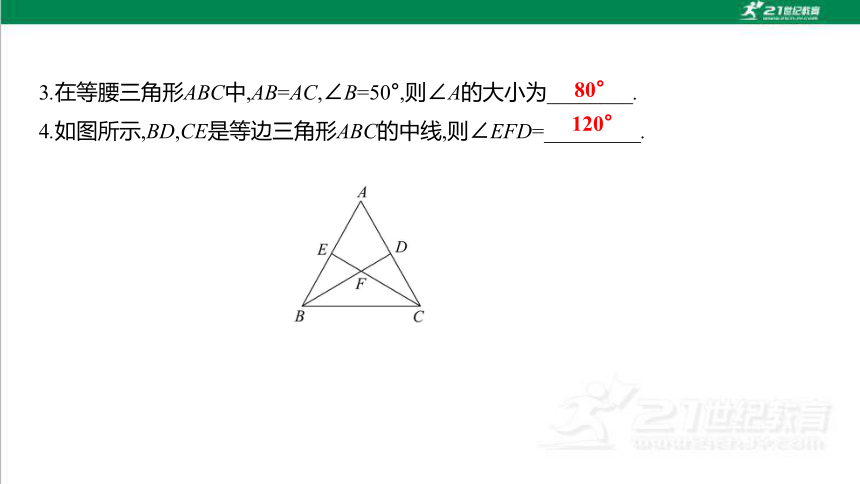
3.在等腰三角形ABC中,AB=AC,∠B=50°,则∠A的大小为________.
4.如图所示,BD,CE是等边三角形ABC的中线,则∠EFD=_________.
80°
120°
等腰三角形的性质
【典例1】(教材再开发·P128随堂练习T2拓展)
(2024·茂名高州期中)已知:△ABC是等腰三角形,AB=AC,AD是底边BC上的高,下列结论中,不一定成立的是( )
A.BD=CD B.BD=AD
C.AD平分∠BAC D.∠B=∠C
【自主解答】选B.因为AB=AC,所以∠B=∠C.
因为AD是底边BC上的高,
所以BD=CD,AD平分∠BAC.
所以A,C,D选项正确,一定成立,不符合题意;B选项不一定成立,符合题意.
1.(2024·河源期末)等腰三角形的一个内角为80°,则这个等腰三角形的底角为( )
A.80°或50° B.80°
C.50° D.50°或20°
A
【解析】分两种情况:
①当80°的角为等腰三角形的顶角时,
底角的度数为(180°-80°)÷2=50°.
②当80°的角为等腰三角形的底角时,其底角为80°.
综上,它的底角为50°或80°.
2.(2024·东莞期末)一个等腰三角形的周长为30 cm.
(1)已知腰长是底边长的2倍,求各边的长.
(2)已知其中一边的长为7 cm,求其他两边的长.
等边三角形的性质
【典例2】(教材再开发·P128“思考·交流”强化)
如图所示,等边三角形DEF的顶点分别在等边三角形ABC的各边上,且BD=2BE, DE⊥BC于点E.若AB=1,求DB的长.
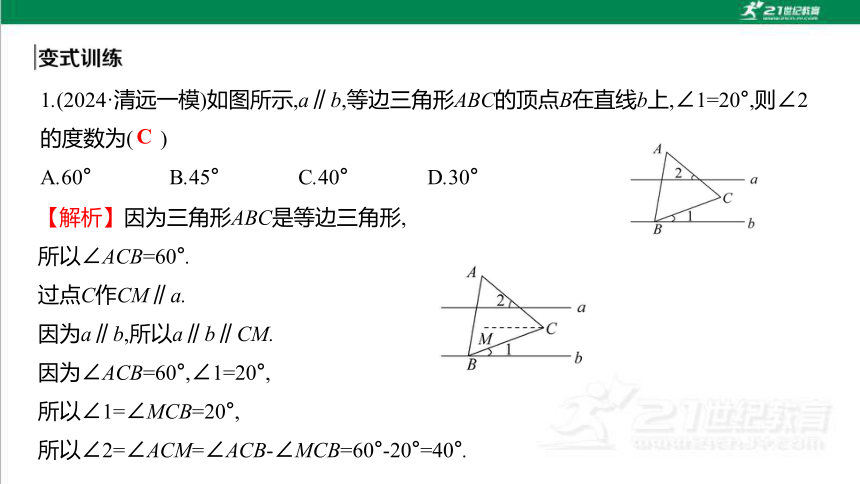
1.(2024·清远一模)如图所示,a∥b,等边三角形ABC的顶点B在直线b上,∠1=20°,则∠2
的度数为( )
A.60° B.45° C.40° D.30°
C
【解析】因为三角形ABC是等边三角形,
所以∠ACB=60°.
过点C作CM∥a.
因为a∥b,所以a∥b∥CM.
因为∠ACB=60°,∠1=20°,
所以∠1=∠MCB=20°,
所以∠2=∠ACM=∠ACB-∠MCB=60°-20°=40°.
2.(2024·深圳福田期末)如图所示,△ABC是等边三角形,D,E分别是AC,BC上的点.若
AE=AD,∠CED=20°,则∠BAE=_______°.
40
【解析】因为△ABC是等边三角形,
所以∠C=∠BAC=60°.
因为∠CED=20°,
所以∠ADE=∠CED+∠C=80°.
因为AE=AD,
所以∠AED=∠ADE=80°,
所以∠DAE=180°-∠AED-∠ADE=20°,
所以∠BAE=∠BAC-∠DAE=60°-20°=40°.
1.若等腰三角形的两边长分别为2和5,则它的周长为( )
A.9 B.7 C.12 D.9或12
C
【解析】(1)若2为腰长,5为底边长,因为2+2<5,所以三角形不存在;
(2)若5为腰长,则符合三角形的两边之和大于第三边,所以这个三角形的周长为5+5+2=12.
2.(2024·韶关期末)如图所示,BD是等边三角形ABC的边AC上的高,以点D为圆心,DB
长为半径作弧交BC的延长线于点E,则∠DEC=( )
A.20° B.25° C.30° D.35°
C
3.如图所示,在△ABC中,D,E分别是△ABC的边AB,AC上的点,已知DE∥BC且DB=DE.
(1)求证:BE是△ABC的角平分线.
(2)若∠A=65°,∠C=45°,求∠AEB的度数.
【解析】(1)证明:因为DE∥BC,
所以∠DEB=∠CBE.
因为DB=DE,所以∠DBE=∠DEB,
所以∠CBE=∠DBE,
所以BE是△ABC的角平分线.
(2)因为∠A=65°,∠C=45°,所以∠ABC=70°.因为BE是△ABC的角平分线,所以∠ABE=35°,所以∠AEB=180°-∠A-∠ABE=80°.
知识点1 等腰三角形
1.(2024·深圳福田期中)等腰三角形的一边长为3 cm,另一边长为7 cm,则它的周长为
( )
A.13 cm B.17 cm
C.22 cm D.13 cm或17 cm
B
【解析】分两种情况:
当腰为3 cm时,3+3=6<7,所以不能构成三角形;
当腰为7 cm时,3+7>7,所以能构成三角形,周长是3+7+7=17(cm).
2.如图所示,直线l1∥l2,AB=BC,CD⊥AB于点D.若∠1=65°,则∠DCA的度数为( )
A.65° B.25° C.15° D.35°
B
【解析】因为∠1=65°,l1∥l2,
所以∠ACB=65°.
因为AB=BC,
所以∠BAC=65°.
因为CD⊥AB,
所以∠DCA=90°-∠BAC=25°.
知识点2 等边三角形
3.(2024·茂名信宜期末)如图所示,直线m∥n,△ABC是等边三角形,顶点B在直线n上,直
线m交AB于点E,交AC于点F.若∠1=140°,则∠2的度数是( )
A.110° B.105° C.100° D.95°
C
【解析】如图所示:
因为△ABC为等边三角形,
所以∠A=60°.
因为∠1+∠AFE=∠A+∠AEF+∠AFE=180°,∠1=140°,
所以∠1=∠A+∠AEF,
所以∠AEF=∠1-∠A=140°-∠A=140°-60°=80°,
所以∠DEB=∠AEF=80°.
因为直线m∥n,
所以∠DEB+∠2=180°,
所以∠2=180°-∠DEB=180°-80°=100°.
4.如图所示,在△ABC中,AB=AC,点D为△ABC内一点,且AD平分∠BAC.
(1)求证:△ABD≌△ACD.
(2)若AB=BC,∠DBC=40°,求∠ACD的度数.
【解析】(1)证明:因为AD平分∠BAC,
所以∠BAD=∠CAD.
又因为AB=AC,AD=AD.
所以△ABD≌△ACD(SAS).
(2)因为AB=AC,AB=BC,所以AB=AC=BC,所以△ABC是等边三角形,所以∠ABC=∠BCA=∠BAC=60°.又因为∠DBC=40°,所以∠ABD=∠ABC-∠DBC=20°.因为△ABD≌△ACD,所以∠ACD=∠ABD=20°.
5.如图所示,△ABC为等边三角形,△ACD为等腰直角三角形,AC=CD,则直线BC与直线
AD的夹角为( )
A.10° B.15° C.20° D.30°
B
【解析】延长AD与BC交于点E,如图所示:
因为△ABC为等边三角形,
所以∠ABC=∠BAC=60°.
又因为△ACD为等腰直角三角形,AC=CD,
所以∠CAD=45°,
所以∠BAD=∠BAC+∠CAD=60°+45°=105°,
所以∠E=180°-(∠ABC+∠BAD)=180°-(60°+105°)=15°,
即直线BC与直线AD的夹角为15°.
6.如图所示是由9个等边三角形拼成的六边形,中间最小的等边三角形的周长是12,这
个六边形的周长是________.
120
【解析】如图所示,
因为中间最小的等边三角形的周长是12,
所以中间最小的等边三角形的边长是4.
设②,③,④的边长为x,则⑤,⑥的边长为x+4,⑦,⑧的边长为x+8,⑨的边长为x+12.
由图可知:2x=x+12,
解得x=12.
所以这个六边形的周长为2x+2(x+4)+2(x+8)+x+12=7x+36=120.
7.(2024·中山期中)如图所示,△ABC是等边三角形,BD是中线,延长BC至E,使CE=CD, DF⊥BE,垂足为点F.
(1)试说明:DB=DE.
(2)若CF=4,求△ABC的周长.
(2)因为DF⊥BE,
所以∠DFC=90°,
所以∠FDC=90°-∠C=30°.
因为CF=4,
所以DC=2CF=8.
因为△ABC为等边三角形,BD是中线,
所以AB=BC=AC=2DC=16,
所以△ABC的周长=AB+AC+BC=3×16=48.
8.如图1所示,在△ABC中,过点B作BD⊥AB,且BD=AB,连接CD.
[问题原型](1)若∠ACB=90°,且AC=BC=8,过点D作△BCD的BC边上的高DE,易证△ABC≌△BDE,从而得到△BCD的面积为 .
[变式探究](2)如图2所示,若∠ACB=90°,BC=a,用含a的代数式表示△BCD的面积,并说明理由.
[拓展应用](3)如图3所示,若AB=AC,BC=8,则△BCD的面积为 .
2 简单的轴对称图形
第1课时
课时目标 素养达成
1.探索并了解等腰三角形的轴对称性及其相关性质 推理能力、几何直观
2.经历探索简单图形的轴对称性的过程,进一步理解轴对称的性质,积累数学活动经验 空间观念
1.如图所示,AD是等腰三角形ABC的顶角平分线,BD=5,则CD等于( )
A.10 B.5 C.4 D.3
2.两边长分别为4,8的等腰三角形的周长为( )
A.16 B.20 C.16或20 D.16或18
B
B
3.在等腰三角形ABC中,AB=AC,∠B=50°,则∠A的大小为________.
4.如图所示,BD,CE是等边三角形ABC的中线,则∠EFD=_________.
80°
120°
等腰三角形的性质
【典例1】(教材再开发·P128随堂练习T2拓展)
(2024·茂名高州期中)已知:△ABC是等腰三角形,AB=AC,AD是底边BC上的高,下列结论中,不一定成立的是( )
A.BD=CD B.BD=AD
C.AD平分∠BAC D.∠B=∠C
【自主解答】选B.因为AB=AC,所以∠B=∠C.
因为AD是底边BC上的高,
所以BD=CD,AD平分∠BAC.
所以A,C,D选项正确,一定成立,不符合题意;B选项不一定成立,符合题意.
1.(2024·河源期末)等腰三角形的一个内角为80°,则这个等腰三角形的底角为( )
A.80°或50° B.80°
C.50° D.50°或20°
A
【解析】分两种情况:
①当80°的角为等腰三角形的顶角时,
底角的度数为(180°-80°)÷2=50°.
②当80°的角为等腰三角形的底角时,其底角为80°.
综上,它的底角为50°或80°.
2.(2024·东莞期末)一个等腰三角形的周长为30 cm.
(1)已知腰长是底边长的2倍,求各边的长.
(2)已知其中一边的长为7 cm,求其他两边的长.
等边三角形的性质
【典例2】(教材再开发·P128“思考·交流”强化)
如图所示,等边三角形DEF的顶点分别在等边三角形ABC的各边上,且BD=2BE, DE⊥BC于点E.若AB=1,求DB的长.
1.(2024·清远一模)如图所示,a∥b,等边三角形ABC的顶点B在直线b上,∠1=20°,则∠2
的度数为( )
A.60° B.45° C.40° D.30°
C
【解析】因为三角形ABC是等边三角形,
所以∠ACB=60°.
过点C作CM∥a.
因为a∥b,所以a∥b∥CM.
因为∠ACB=60°,∠1=20°,
所以∠1=∠MCB=20°,
所以∠2=∠ACM=∠ACB-∠MCB=60°-20°=40°.
2.(2024·深圳福田期末)如图所示,△ABC是等边三角形,D,E分别是AC,BC上的点.若
AE=AD,∠CED=20°,则∠BAE=_______°.
40
【解析】因为△ABC是等边三角形,
所以∠C=∠BAC=60°.
因为∠CED=20°,
所以∠ADE=∠CED+∠C=80°.
因为AE=AD,
所以∠AED=∠ADE=80°,
所以∠DAE=180°-∠AED-∠ADE=20°,
所以∠BAE=∠BAC-∠DAE=60°-20°=40°.
1.若等腰三角形的两边长分别为2和5,则它的周长为( )
A.9 B.7 C.12 D.9或12
C
【解析】(1)若2为腰长,5为底边长,因为2+2<5,所以三角形不存在;
(2)若5为腰长,则符合三角形的两边之和大于第三边,所以这个三角形的周长为5+5+2=12.
2.(2024·韶关期末)如图所示,BD是等边三角形ABC的边AC上的高,以点D为圆心,DB
长为半径作弧交BC的延长线于点E,则∠DEC=( )
A.20° B.25° C.30° D.35°
C
3.如图所示,在△ABC中,D,E分别是△ABC的边AB,AC上的点,已知DE∥BC且DB=DE.
(1)求证:BE是△ABC的角平分线.
(2)若∠A=65°,∠C=45°,求∠AEB的度数.
【解析】(1)证明:因为DE∥BC,
所以∠DEB=∠CBE.
因为DB=DE,所以∠DBE=∠DEB,
所以∠CBE=∠DBE,
所以BE是△ABC的角平分线.
(2)因为∠A=65°,∠C=45°,所以∠ABC=70°.因为BE是△ABC的角平分线,所以∠ABE=35°,所以∠AEB=180°-∠A-∠ABE=80°.
知识点1 等腰三角形
1.(2024·深圳福田期中)等腰三角形的一边长为3 cm,另一边长为7 cm,则它的周长为
( )
A.13 cm B.17 cm
C.22 cm D.13 cm或17 cm
B
【解析】分两种情况:
当腰为3 cm时,3+3=6<7,所以不能构成三角形;
当腰为7 cm时,3+7>7,所以能构成三角形,周长是3+7+7=17(cm).
2.如图所示,直线l1∥l2,AB=BC,CD⊥AB于点D.若∠1=65°,则∠DCA的度数为( )
A.65° B.25° C.15° D.35°
B
【解析】因为∠1=65°,l1∥l2,
所以∠ACB=65°.
因为AB=BC,
所以∠BAC=65°.
因为CD⊥AB,
所以∠DCA=90°-∠BAC=25°.
知识点2 等边三角形
3.(2024·茂名信宜期末)如图所示,直线m∥n,△ABC是等边三角形,顶点B在直线n上,直
线m交AB于点E,交AC于点F.若∠1=140°,则∠2的度数是( )
A.110° B.105° C.100° D.95°
C
【解析】如图所示:
因为△ABC为等边三角形,
所以∠A=60°.
因为∠1+∠AFE=∠A+∠AEF+∠AFE=180°,∠1=140°,
所以∠1=∠A+∠AEF,
所以∠AEF=∠1-∠A=140°-∠A=140°-60°=80°,
所以∠DEB=∠AEF=80°.
因为直线m∥n,
所以∠DEB+∠2=180°,
所以∠2=180°-∠DEB=180°-80°=100°.
4.如图所示,在△ABC中,AB=AC,点D为△ABC内一点,且AD平分∠BAC.
(1)求证:△ABD≌△ACD.
(2)若AB=BC,∠DBC=40°,求∠ACD的度数.
【解析】(1)证明:因为AD平分∠BAC,
所以∠BAD=∠CAD.
又因为AB=AC,AD=AD.
所以△ABD≌△ACD(SAS).
(2)因为AB=AC,AB=BC,所以AB=AC=BC,所以△ABC是等边三角形,所以∠ABC=∠BCA=∠BAC=60°.又因为∠DBC=40°,所以∠ABD=∠ABC-∠DBC=20°.因为△ABD≌△ACD,所以∠ACD=∠ABD=20°.
5.如图所示,△ABC为等边三角形,△ACD为等腰直角三角形,AC=CD,则直线BC与直线
AD的夹角为( )
A.10° B.15° C.20° D.30°
B
【解析】延长AD与BC交于点E,如图所示:
因为△ABC为等边三角形,
所以∠ABC=∠BAC=60°.
又因为△ACD为等腰直角三角形,AC=CD,
所以∠CAD=45°,
所以∠BAD=∠BAC+∠CAD=60°+45°=105°,
所以∠E=180°-(∠ABC+∠BAD)=180°-(60°+105°)=15°,
即直线BC与直线AD的夹角为15°.
6.如图所示是由9个等边三角形拼成的六边形,中间最小的等边三角形的周长是12,这
个六边形的周长是________.
120
【解析】如图所示,
因为中间最小的等边三角形的周长是12,
所以中间最小的等边三角形的边长是4.
设②,③,④的边长为x,则⑤,⑥的边长为x+4,⑦,⑧的边长为x+8,⑨的边长为x+12.
由图可知:2x=x+12,
解得x=12.
所以这个六边形的周长为2x+2(x+4)+2(x+8)+x+12=7x+36=120.
7.(2024·中山期中)如图所示,△ABC是等边三角形,BD是中线,延长BC至E,使CE=CD, DF⊥BE,垂足为点F.
(1)试说明:DB=DE.
(2)若CF=4,求△ABC的周长.
(2)因为DF⊥BE,
所以∠DFC=90°,
所以∠FDC=90°-∠C=30°.
因为CF=4,
所以DC=2CF=8.
因为△ABC为等边三角形,BD是中线,
所以AB=BC=AC=2DC=16,
所以△ABC的周长=AB+AC+BC=3×16=48.
8.如图1所示,在△ABC中,过点B作BD⊥AB,且BD=AB,连接CD.
[问题原型](1)若∠ACB=90°,且AC=BC=8,过点D作△BCD的BC边上的高DE,易证△ABC≌△BDE,从而得到△BCD的面积为 .
[变式探究](2)如图2所示,若∠ACB=90°,BC=a,用含a的代数式表示△BCD的面积,并说明理由.
[拓展应用](3)如图3所示,若AB=AC,BC=8,则△BCD的面积为 .
同课章节目录
