5.2.2 简单的轴对称图形 第2课时 课件(共27张PPT)
文档属性
| 名称 | 5.2.2 简单的轴对称图形 第2课时 课件(共27张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 17:05:59 | ||
图片预览






文档简介
(共27张PPT)
2 简单的轴对称图形
第2课时
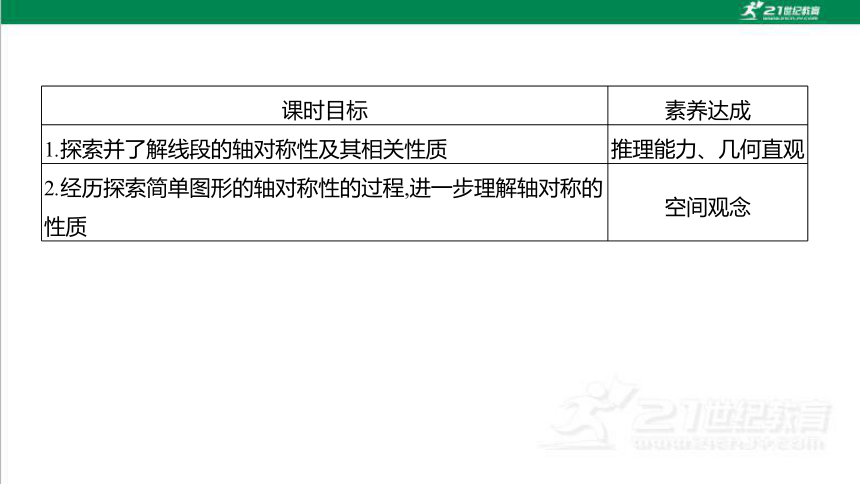
课时目标 素养达成
1.探索并了解线段的轴对称性及其相关性质 推理能力、几何直观
2.经历探索简单图形的轴对称性的过程,进一步理解轴对称的性质 空间观念
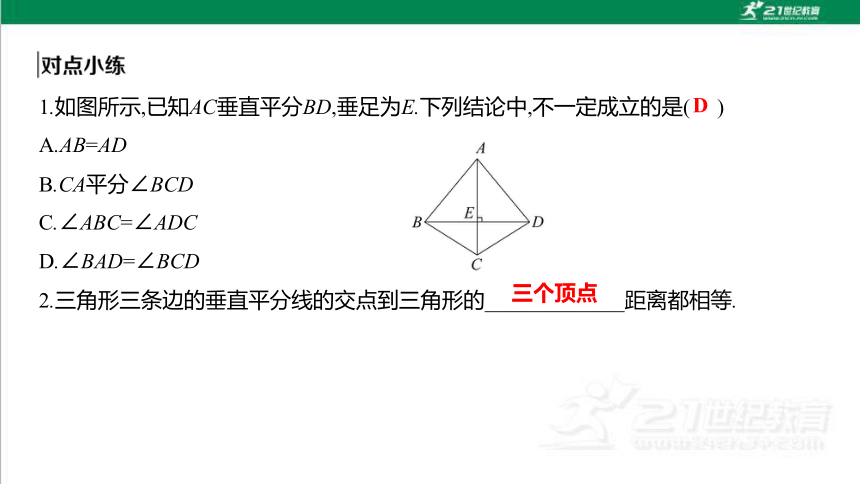
1.如图所示,已知AC垂直平分BD,垂足为E.下列结论中,不一定成立的是( )
A.AB=AD
B.CA平分∠BCD
C.∠ABC=∠ADC
D.∠BAD=∠BCD
2.三角形三条边的垂直平分线的交点到三角形的_____________距离都相等.
D
三个顶点
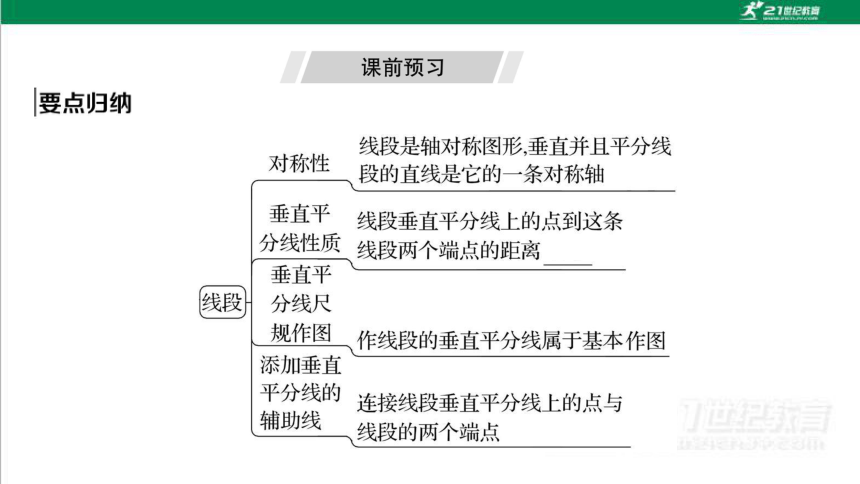
线段垂直平分线的性质
【典例1】(教材再开发·P129“尝试·思考”拓展)
(2024·梅州大埔期末)如图所示,在△ABC中,AB=AC,AB的垂直平分线交AC于点P.
(1)若∠A=35°,求∠BPC的度数.
(2)若AB=5 cm,BC=3 cm,求△PBC的周长.
【自主解答】(1)因为AB的垂直平分线交AC于点P,
所以AP=BP,
所以∠A=∠ABP=35°,
所以∠APB=180°-∠A-∠ABP=110°,
所以∠BPC=180°-∠APB=70°.
(2)△PBC的周长为BP+PC+BC=AP+PC+BC=AC+BC=AB+BC.
因为AB=5 cm,BC=3 cm,
所以△PBC的周长为5+3=8(cm).
(2024·佛山禅城期末)如图所示,在△ABC中,∠C=90°,点P在AC上,点D在AB上,PD=PA,BD的垂直平分线交BC于点E,交BD于点F,连接DE.试说明:DE⊥DP.
【解析】因为PD=PA,所以∠PDA=∠A.
因为EF垂直平分BD,所以ED=EB,
所以∠EDB=∠B.
在Rt△ABC中,∠ACB=90°,
所以∠A+∠B=90°,
所以∠PDA+∠EDB=90°,
所以∠PDE=90°,所以DE⊥PD.
用尺规作线段的垂直平分线
【典例2】如图所示,已知在△ABC中,AB=4,AC=7.
(1)用尺规作BC边的垂直平分线.(保留作图痕迹,不写作法)
(2)若BC边的垂直平分线交AC于D,交BC于E.
①连接BD,求△ABD的周长.
②若∠ADB=52°,求∠DBC的度数.
【自主解答】(1)如图所示,即为所求.
(2)①因为DE是BC边的垂直平分线,
所以BD=DC.因为AB=4,AC=7,
所以△ABD的周长为AB+BD+AD=AB+AC=4+7=11.
②因为BD=CD,所以∠DBC=∠C,所以∠ADB=∠DBC+∠C=52°,所以∠DBC=26°.
(2024·惠州惠阳质检)如图所示,在△ABC中,AB>AC.
(1)用直尺和圆规作BC的垂直平分线,交AB于点D.(要求保留作图痕迹)
(2)连接CD,若AB=8,AC=4,求△ACD的周长.
【解析】(1)如图所示:
直线MN即为所求.
(2)由(1)可知,直线MN是线段BC的垂直平分线,
所以DC=DB,
所以△ACD的周长为AC+CD+AD=AC+AD+BD=AC+AB.
因为AB=8,AC=4,
所以△ACD的周长为8+4=12.
B
【解析】根据作图可知直线MN为BC的垂直平分线,所以BD=CD.
因为AC=55,AD=15,
所以BD=CD=AC-AD=55-15=40.
A
【解析】∠BAC=180°-∠B-∠C=95°.
由作图可知,直线MN是线段AC的垂直平分线,所以DA=DC,
所以∠DAC=∠C=35°,
所以∠BAD=∠BAC-∠DAC=95°-35°=60°.
知识点1 线段垂直平分线
1.(2024·揭阳榕城期末)如图所示,在△ABC中,AC的垂直平分线交AB于点D,垂足为点
E,CD平分∠ACB.若∠A=50°,则∠B的度数为( )
A.25° B.30° C.35° D.40°
B
【解析】因为DE垂直平分AC,
所以AD=CD,
所以∠A=∠ACD.
又因为CD平分∠ACB,∠A=50°,
所以∠ACB=2∠ACD=100°,
所以∠B=180°-∠A-∠ACB=180°-50°-100°=30°.
C
【解析】由作图知,EF垂直平分AB,所以AD=BD,所以△BCD的周长为BD+CD+BC=AD+CD+BC=AC+BC.因为AB=AC=6,BC=4,所以△BCD的周长为6+4=10.
A
【解析】因为AB=AC,所以∠ABC=∠ACB.
由作图可知,MN垂直平分AC,
因为直线MN恰好经过点D,
所以AD=CD,所以∠A=∠ACD,
又因为∠ADC=90°,所以∠ACD=45°.
因为∠CDB=90°,所以∠B+∠BCD=90°,
所以∠ACB+∠BCD=90°,
所以∠BCD+∠ACD+∠BCD=90°,
所以2∠BCD+45°=90°,
所以∠BCD=22.5°.
16
【解析】由作图可得AD=AC=7,MN垂直平分BD,
所以EB=ED,
所以△ADE的周长为AE+DE+AD=AE+BE+AD=AB+AD=16.
5.(2024·西安质检)已知△ABC.求作:BC边上的中线AD,AD交BC于点D.
(说明:只允许尺规作图,不写作法,保留作图痕迹)
【解析】如图所示,作线段BC的垂直平分线,交BC于点D,连接AD,
则AD即为所求.
6.(2024·佛山禅城期末)如图所示,在△ABC中,AB=AE,且AD⊥BC,EF垂直平分AC,交AC
于点F,交BC于点E.若△ABC的周长为16,AC=6,则DC为( )
A.5 B.8 C.9 D.10
A
7.如图所示,在△ABC中,DM,EN分别垂直平分AB和AC,交BC于点D,E.
(1)若∠DAE=50°,求∠BAC的度数.
(2)若△ADE的周长为19 cm,求BC的长度.
【解析】(1)因为DM,EN分别垂直平分AB和AC,
所以AD=BD,AE=EC,
所以∠B=∠BAD,∠C=∠EAC.
因为∠BAC=∠DAE+∠BAD+∠CAE,
所以∠BAC=∠DAE+∠B+∠C.
又因为∠BAC+∠B+∠C=180°,
∠DAE=50°,所以∠BAC=115°.
(2)因为△ADE的周长为19 cm,
所以AD+AE+DE=19 cm.
由(1)知,AD=BD,AE=EC,
所以BD+DE+EC=19 cm,即BC=19 cm.
8.如图所示,在Rt△ABC中,∠A=90°,过点B作BH∥AC.
(1)用尺规作线段BC的垂直平分线,交AC于点E,交BC于点F,交BH于点D,连接BE,CD.(要求:保留作图痕迹,不写作法,不下结论)
(2)求证:BE=BD.
2 简单的轴对称图形
第2课时
课时目标 素养达成
1.探索并了解线段的轴对称性及其相关性质 推理能力、几何直观
2.经历探索简单图形的轴对称性的过程,进一步理解轴对称的性质 空间观念
1.如图所示,已知AC垂直平分BD,垂足为E.下列结论中,不一定成立的是( )
A.AB=AD
B.CA平分∠BCD
C.∠ABC=∠ADC
D.∠BAD=∠BCD
2.三角形三条边的垂直平分线的交点到三角形的_____________距离都相等.
D
三个顶点
线段垂直平分线的性质
【典例1】(教材再开发·P129“尝试·思考”拓展)
(2024·梅州大埔期末)如图所示,在△ABC中,AB=AC,AB的垂直平分线交AC于点P.
(1)若∠A=35°,求∠BPC的度数.
(2)若AB=5 cm,BC=3 cm,求△PBC的周长.
【自主解答】(1)因为AB的垂直平分线交AC于点P,
所以AP=BP,
所以∠A=∠ABP=35°,
所以∠APB=180°-∠A-∠ABP=110°,
所以∠BPC=180°-∠APB=70°.
(2)△PBC的周长为BP+PC+BC=AP+PC+BC=AC+BC=AB+BC.
因为AB=5 cm,BC=3 cm,
所以△PBC的周长为5+3=8(cm).
(2024·佛山禅城期末)如图所示,在△ABC中,∠C=90°,点P在AC上,点D在AB上,PD=PA,BD的垂直平分线交BC于点E,交BD于点F,连接DE.试说明:DE⊥DP.
【解析】因为PD=PA,所以∠PDA=∠A.
因为EF垂直平分BD,所以ED=EB,
所以∠EDB=∠B.
在Rt△ABC中,∠ACB=90°,
所以∠A+∠B=90°,
所以∠PDA+∠EDB=90°,
所以∠PDE=90°,所以DE⊥PD.
用尺规作线段的垂直平分线
【典例2】如图所示,已知在△ABC中,AB=4,AC=7.
(1)用尺规作BC边的垂直平分线.(保留作图痕迹,不写作法)
(2)若BC边的垂直平分线交AC于D,交BC于E.
①连接BD,求△ABD的周长.
②若∠ADB=52°,求∠DBC的度数.
【自主解答】(1)如图所示,即为所求.
(2)①因为DE是BC边的垂直平分线,
所以BD=DC.因为AB=4,AC=7,
所以△ABD的周长为AB+BD+AD=AB+AC=4+7=11.
②因为BD=CD,所以∠DBC=∠C,所以∠ADB=∠DBC+∠C=52°,所以∠DBC=26°.
(2024·惠州惠阳质检)如图所示,在△ABC中,AB>AC.
(1)用直尺和圆规作BC的垂直平分线,交AB于点D.(要求保留作图痕迹)
(2)连接CD,若AB=8,AC=4,求△ACD的周长.
【解析】(1)如图所示:
直线MN即为所求.
(2)由(1)可知,直线MN是线段BC的垂直平分线,
所以DC=DB,
所以△ACD的周长为AC+CD+AD=AC+AD+BD=AC+AB.
因为AB=8,AC=4,
所以△ACD的周长为8+4=12.
B
【解析】根据作图可知直线MN为BC的垂直平分线,所以BD=CD.
因为AC=55,AD=15,
所以BD=CD=AC-AD=55-15=40.
A
【解析】∠BAC=180°-∠B-∠C=95°.
由作图可知,直线MN是线段AC的垂直平分线,所以DA=DC,
所以∠DAC=∠C=35°,
所以∠BAD=∠BAC-∠DAC=95°-35°=60°.
知识点1 线段垂直平分线
1.(2024·揭阳榕城期末)如图所示,在△ABC中,AC的垂直平分线交AB于点D,垂足为点
E,CD平分∠ACB.若∠A=50°,则∠B的度数为( )
A.25° B.30° C.35° D.40°
B
【解析】因为DE垂直平分AC,
所以AD=CD,
所以∠A=∠ACD.
又因为CD平分∠ACB,∠A=50°,
所以∠ACB=2∠ACD=100°,
所以∠B=180°-∠A-∠ACB=180°-50°-100°=30°.
C
【解析】由作图知,EF垂直平分AB,所以AD=BD,所以△BCD的周长为BD+CD+BC=AD+CD+BC=AC+BC.因为AB=AC=6,BC=4,所以△BCD的周长为6+4=10.
A
【解析】因为AB=AC,所以∠ABC=∠ACB.
由作图可知,MN垂直平分AC,
因为直线MN恰好经过点D,
所以AD=CD,所以∠A=∠ACD,
又因为∠ADC=90°,所以∠ACD=45°.
因为∠CDB=90°,所以∠B+∠BCD=90°,
所以∠ACB+∠BCD=90°,
所以∠BCD+∠ACD+∠BCD=90°,
所以2∠BCD+45°=90°,
所以∠BCD=22.5°.
16
【解析】由作图可得AD=AC=7,MN垂直平分BD,
所以EB=ED,
所以△ADE的周长为AE+DE+AD=AE+BE+AD=AB+AD=16.
5.(2024·西安质检)已知△ABC.求作:BC边上的中线AD,AD交BC于点D.
(说明:只允许尺规作图,不写作法,保留作图痕迹)
【解析】如图所示,作线段BC的垂直平分线,交BC于点D,连接AD,
则AD即为所求.
6.(2024·佛山禅城期末)如图所示,在△ABC中,AB=AE,且AD⊥BC,EF垂直平分AC,交AC
于点F,交BC于点E.若△ABC的周长为16,AC=6,则DC为( )
A.5 B.8 C.9 D.10
A
7.如图所示,在△ABC中,DM,EN分别垂直平分AB和AC,交BC于点D,E.
(1)若∠DAE=50°,求∠BAC的度数.
(2)若△ADE的周长为19 cm,求BC的长度.
【解析】(1)因为DM,EN分别垂直平分AB和AC,
所以AD=BD,AE=EC,
所以∠B=∠BAD,∠C=∠EAC.
因为∠BAC=∠DAE+∠BAD+∠CAE,
所以∠BAC=∠DAE+∠B+∠C.
又因为∠BAC+∠B+∠C=180°,
∠DAE=50°,所以∠BAC=115°.
(2)因为△ADE的周长为19 cm,
所以AD+AE+DE=19 cm.
由(1)知,AD=BD,AE=EC,
所以BD+DE+EC=19 cm,即BC=19 cm.
8.如图所示,在Rt△ABC中,∠A=90°,过点B作BH∥AC.
(1)用尺规作线段BC的垂直平分线,交AC于点E,交BC于点F,交BH于点D,连接BE,CD.(要求:保留作图痕迹,不写作法,不下结论)
(2)求证:BE=BD.
同课章节目录
