5.2.3 简单的轴对称图形 第3课时 课件(共33张PPT)
文档属性
| 名称 | 5.2.3 简单的轴对称图形 第3课时 课件(共33张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 17:13:54 | ||
图片预览








文档简介
(共33张PPT)
2 简单的轴对称图形
第3课时
课时目标 素养达成
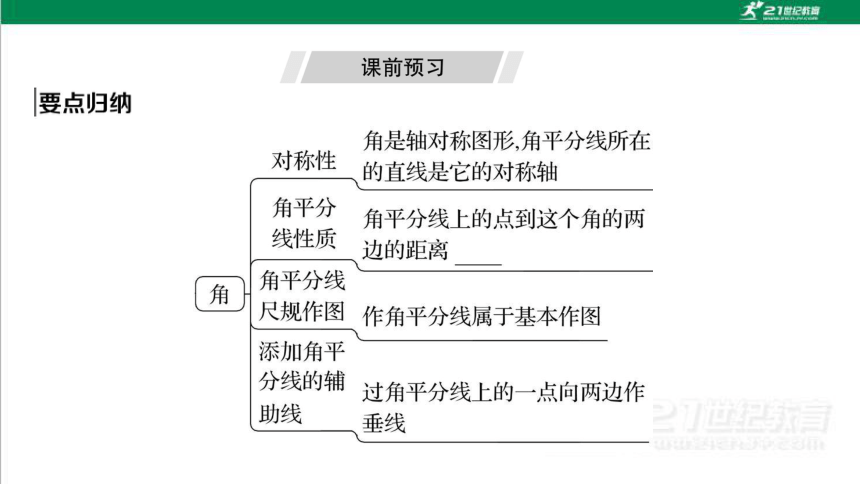
1.了解角是轴对称图形,掌握角平分线的性质,能应用角平分线的性质解决简单的问题 几何直观、推理能力
2.能借助尺规作出一个角的平分线 几何直观、空间观念
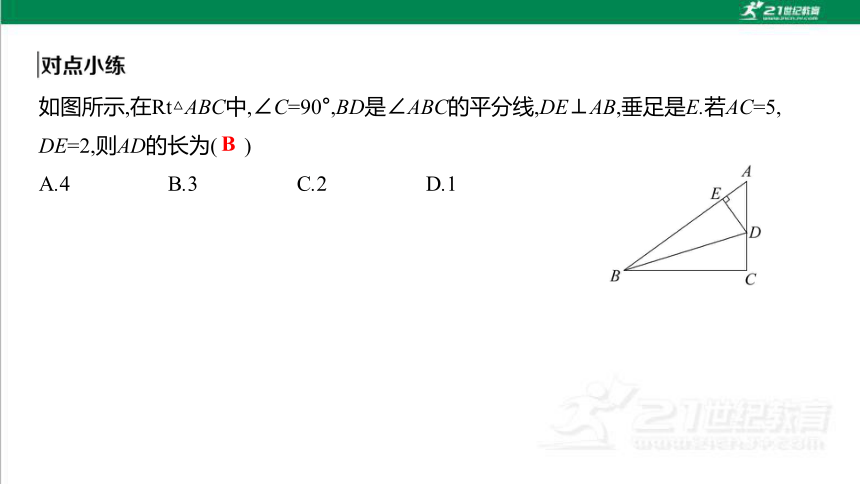
如图所示,在Rt△ABC中,∠C=90°,BD是∠ABC的平分线,DE⊥AB,垂足是E.若AC=5,
DE=2,则AD的长为( )
A.4 B.3 C.2 D.1
B
角平分线
【典例1】
已知,如图所示,BD是∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD,PN⊥CD,垂足分别是M,N.试说明:PM=PN.
(2024·深圳龙岗期中)如图所示,在△ABC中,∠C=90°,BD平分∠ABC,交AC于点D,AC=
15 cm,AD=9 cm,DE⊥AB,则DE=( )
A.9 cm B.7 cm
C.6 cm D.5 cm
C
【解析】因为AC=15 cm,AD=9 cm,
所以CD=AC-AD=6 cm.
因为BD平分∠ABC,且∠C=90°,DE⊥AB,
所以DE=CD=6 cm.
用尺规作角的平分线
【典例2】如图所示,在△ABC中,AB=AC,∠ABC=76°.
(1)用直尺和圆规作∠ABC的平分线BD交AC于点D(保留作图痕迹,不要求写作法).
(2)在(1)中作出∠ABC的平分线BD后,求∠BDC的度数.
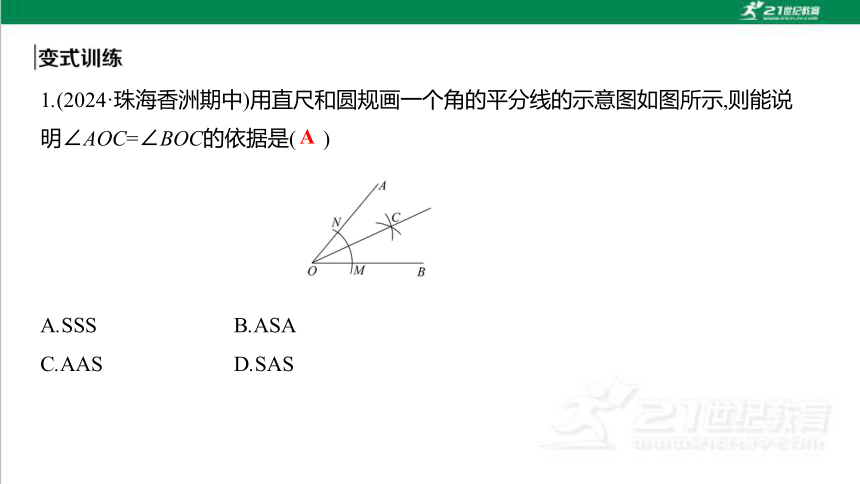
1.(2024·珠海香洲期中)用直尺和圆规画一个角的平分线的示意图如图所示,则能说
明∠AOC=∠BOC的依据是( )
A.SSS B.ASA
C.AAS D.SAS
A
A
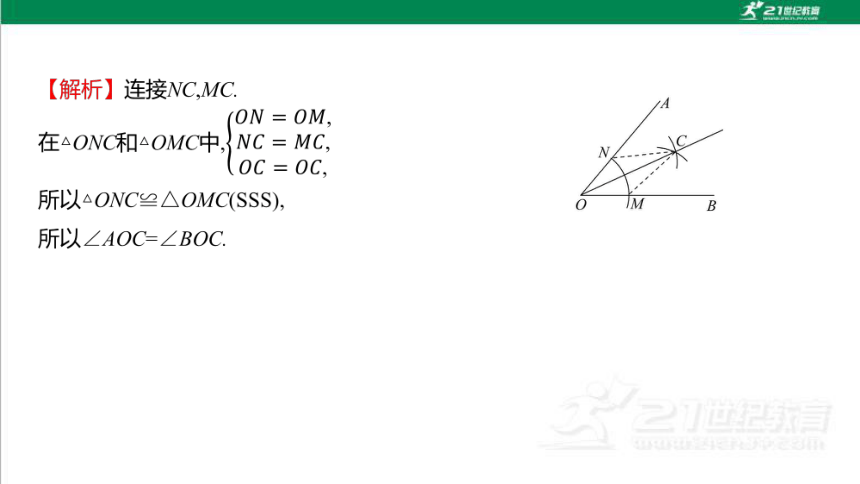
【解析】A.以C,D为圆心画弧的半径相等,因此CM=DM,又OC=OD,OM=OM,
因此△OCM≌△ODM(SSS),得到∠1=∠2,故A符合题意;
B.因为OC,CM的长在变化,所以OC和CM不一定相等,因此∠1不一定等于∠3,故B不符合题意;
C.因为OD,DM的长在变化,所以OD和DM不一定相等,故C不符合题意;
D.因为CM的位置在变化,所以CM和OB不一定平行,因此∠2不一定等于∠3,故D不符合题意.
B
2.如图所示,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,若AD=2,BC=8,则
△BCD的面积为______.
8
3.电信部门要修建一座电视信号发射塔,如图所示,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条高速公路OM,ON的距离也必须相等,发射塔P应修建在什么位置
【解析】如图所示,作AB的垂直平分线与∠MON或∠QON的平分线,交点P1,P2即为所求发射塔应修建的位置.
知识点1 角平分线
1.(2024·佛山顺德质检)如图所示,OP平分∠AOB,PC⊥OA于点C,点D在OB上.若PC=
2,OD=4,则△POD的面积为( )
A.4 B.6 C.8 D.12
A
2.(2024·济南质检)如图所示,在△ABC中,∠B=∠C,点D是BC的中点,DE⊥AB,DF⊥AC,
E,F为垂足,求证:点D在∠BAC的平分线上.
知识点2 用尺规作角平分线
3.如图所示,在△ABC中,∠C=90°,用直尺和圆规在边BC上确定一点P,使点P到边AC,
AB的距离相等,则符合要求的作图痕迹是( )
C
【解析】因为点P到边AC,AB的距离相等,
所以点P在∠BAC的平分线上.
23
5.(2024·梅州大埔期末)如图所示,AD是△ABC中∠BAC的平分线,DE⊥AB于点E,
S△ABC=28,DE=4,AB=8,则AC的长是______.
6
6.(2024·韶关期末)如图所示,已知△ABC的周长是18 cm,∠ABC和∠ACB的平分线交
于点O,OD⊥BC于点D.若OD=3 cm,则△ABC的面积是( )
A.24 cm2 B.27 cm2 C.30 cm2 D.33 cm2
B
12
8.如图所示,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,点F在AC上,∠FDC=∠BDE.
求证:(1)CF=EB.
(2)AB=AF+2EB.
2 简单的轴对称图形
第3课时
课时目标 素养达成
1.了解角是轴对称图形,掌握角平分线的性质,能应用角平分线的性质解决简单的问题 几何直观、推理能力
2.能借助尺规作出一个角的平分线 几何直观、空间观念
如图所示,在Rt△ABC中,∠C=90°,BD是∠ABC的平分线,DE⊥AB,垂足是E.若AC=5,
DE=2,则AD的长为( )
A.4 B.3 C.2 D.1
B
角平分线
【典例1】
已知,如图所示,BD是∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD,PN⊥CD,垂足分别是M,N.试说明:PM=PN.
(2024·深圳龙岗期中)如图所示,在△ABC中,∠C=90°,BD平分∠ABC,交AC于点D,AC=
15 cm,AD=9 cm,DE⊥AB,则DE=( )
A.9 cm B.7 cm
C.6 cm D.5 cm
C
【解析】因为AC=15 cm,AD=9 cm,
所以CD=AC-AD=6 cm.
因为BD平分∠ABC,且∠C=90°,DE⊥AB,
所以DE=CD=6 cm.
用尺规作角的平分线
【典例2】如图所示,在△ABC中,AB=AC,∠ABC=76°.
(1)用直尺和圆规作∠ABC的平分线BD交AC于点D(保留作图痕迹,不要求写作法).
(2)在(1)中作出∠ABC的平分线BD后,求∠BDC的度数.
1.(2024·珠海香洲期中)用直尺和圆规画一个角的平分线的示意图如图所示,则能说
明∠AOC=∠BOC的依据是( )
A.SSS B.ASA
C.AAS D.SAS
A
A
【解析】A.以C,D为圆心画弧的半径相等,因此CM=DM,又OC=OD,OM=OM,
因此△OCM≌△ODM(SSS),得到∠1=∠2,故A符合题意;
B.因为OC,CM的长在变化,所以OC和CM不一定相等,因此∠1不一定等于∠3,故B不符合题意;
C.因为OD,DM的长在变化,所以OD和DM不一定相等,故C不符合题意;
D.因为CM的位置在变化,所以CM和OB不一定平行,因此∠2不一定等于∠3,故D不符合题意.
B
2.如图所示,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,若AD=2,BC=8,则
△BCD的面积为______.
8
3.电信部门要修建一座电视信号发射塔,如图所示,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条高速公路OM,ON的距离也必须相等,发射塔P应修建在什么位置
【解析】如图所示,作AB的垂直平分线与∠MON或∠QON的平分线,交点P1,P2即为所求发射塔应修建的位置.
知识点1 角平分线
1.(2024·佛山顺德质检)如图所示,OP平分∠AOB,PC⊥OA于点C,点D在OB上.若PC=
2,OD=4,则△POD的面积为( )
A.4 B.6 C.8 D.12
A
2.(2024·济南质检)如图所示,在△ABC中,∠B=∠C,点D是BC的中点,DE⊥AB,DF⊥AC,
E,F为垂足,求证:点D在∠BAC的平分线上.
知识点2 用尺规作角平分线
3.如图所示,在△ABC中,∠C=90°,用直尺和圆规在边BC上确定一点P,使点P到边AC,
AB的距离相等,则符合要求的作图痕迹是( )
C
【解析】因为点P到边AC,AB的距离相等,
所以点P在∠BAC的平分线上.
23
5.(2024·梅州大埔期末)如图所示,AD是△ABC中∠BAC的平分线,DE⊥AB于点E,
S△ABC=28,DE=4,AB=8,则AC的长是______.
6
6.(2024·韶关期末)如图所示,已知△ABC的周长是18 cm,∠ABC和∠ACB的平分线交
于点O,OD⊥BC于点D.若OD=3 cm,则△ABC的面积是( )
A.24 cm2 B.27 cm2 C.30 cm2 D.33 cm2
B
12
8.如图所示,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,点F在AC上,∠FDC=∠BDE.
求证:(1)CF=EB.
(2)AB=AF+2EB.
同课章节目录
