1.4 整式的除法 课件(共29张PPT)
文档属性
| 名称 | 1.4 整式的除法 课件(共29张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 19:31:25 | ||
图片预览








文档简介
(共29张PPT)
4 整式的除法
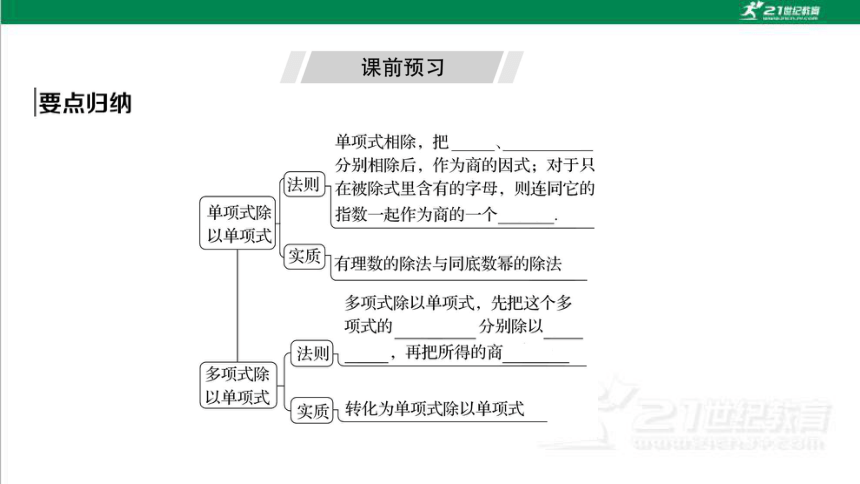
课时目标 素养达成
1.理解单项式除以单项式、多项式除以单项式的运算法则 运算能力、应用意识
2.会进行单项式除以单项式、多项式除以单项式的整式除法运算 抽象能力、推理能力
1.计算6x3÷3x2的结果是( )
A.x B.2x C.2x5 D.2x6
2.计算(25x2y-5xy2)÷5xy的结果等于( )
A.-5x+y B.5x-y
C.-5x+1 D.-5x-1
3.计算:(-9x2+3x)÷(-3x)=_________.
B
B
3x-1
单项式除以单项式(运算能力)
【典例1】(教材再开发·P27例补充)计算:
(1)(2024·广州白云期中)(-2x2y3)3÷(-x2)2.
(2)7.2×1012÷(-3.6×109).
【自主解答】(1)原式=-8x6y9÷x4=-8x2y9.
(2)原式=[7.2÷(-3.6)]×(1012÷109)=-2×103.
1.(2024·深圳龙华质检)25x2y3÷(-5xy)的运算结果是( )
A.-5x2y B.5xy2
C.5x2y D.-5xy2
【解析】25x2y3÷(-5xy)=-5xy2.
D
2.(2024·珠海十一中一模)计算:8x3y÷(2x)2=________.
【解析】原式=8x3y÷4x2=2xy.
2xy
多项式除以单项式(运算能力)
【典例2】(教材再开发·P28习题T1补充)计算:
(1)(2024·河源龙川期末)[(2a)2-4ab+2a]÷2a.
(2)计算:(12m4n-9m2n2+3m3)÷(-3m2).
【自主解答】(1)原式=(4a2-4ab+2a)÷2a=2a-2b+1.
(2)原式=12m4n÷(-3m2)-9m2n2÷(-3m2)+3m3÷(-3m2)=-4m2n+3n2-m.
1.(2024·茂名电白期中)(10x2y-5xy2)÷(-5xy)的结果是( )
A.2x+y B.2x-y
C.-2x-y D.-2x+y
【解析】(10x2y-5xy2)÷(-5xy)
=10x2y÷(-5xy)-5xy2÷(-5xy)
=-2x+y.
D
2.一个长方形的面积是xy2-x2y,若长为xy,那么宽为( )
A.x-y B.y-x
C.x+y D.-x-y
【解析】长方形的宽为:(xy2-x2y)÷xy
=xy2÷xy-x2y÷xy
=y-x.
B
1.(2024·佛山顺德质检)计算(-4x3+2x)÷2x的结果正确的是( )
A.-8x4+4x2 B.-4x3
C.-2x D.-2x2+1
【解析】(-4x3+2x)÷2x=-2x2+1.
D
3.计算:
(1)(2024·深圳南山质检)(-3xy2)2·(-6x2y)÷(9x4y5).
(2)[(3a-b)2+(a+b)(a-b)]÷2a.
【解析】(1)原式=9x2y4·(-6x2y)÷(9x4y5)
=-54x4y5÷(9x4y5)
=-6.
(2)原式=(9a2-6ab+b2+a2-b2)÷2a
=(10a2-6ab)÷2a
=5a-3b.
知识点1 单项式除以单项式
1.计算-14x3y3÷7x2y的结果是( )
A.2x B.-2x C.2y2 D.-2xy2
【解析】原式=[(-14)÷7]·(x3÷x2)·(y3÷y)=-2xy2.
D
2.已知28a3bm÷(28anb2)=b2,那么m,n的值分别为( )
A.4,3 B.4,1 C.1,3 D.2,3
A
知识点2 多项式除以单项式
3.计算(x3-2x2y)÷(-x2)的结果是( )
A.x-2y B.-x+2y
C.-x-2 D.-x+2
【解析】原式=x3÷(-x2)-2x2y÷(-x2)=-x+2y.
B
4.(2024·清远英德期中)计算:(9a3b2-3ab)÷3ab=__________.
【解析】原式=9a3b2÷3ab-3ab÷3ab=3a2b-1.
3a2b-1
5.计算:(12m4n-9m2n2+3m3)÷(-3m2).
【解析】(12m4n-9m2n2+3m3)÷(-3m2)=12m4n÷(-3m2)-9m2n2÷(-3m2)+3m3÷(-3m2)
=-4m2n+3n2-m.
知识点3 整式的混合运算
6.计算[(-a2)3-3a2(-a2)]÷(-a)2的结果是( )
A.-a3+3a2 B.a3-3a2
C.-a4+3a2 D.-a4+a2
【解析】原式=(-a6+3a4)÷a2=-a4+3a2.
C
7.[(x+y)2-(x-y)2]÷4xy=______.
【解析】[(x+y)2-(x-y)2]÷4xy
=[x2+2xy+y2-(x2-2xy+y2)]÷4xy
=(x2+2xy+y2-x2+2xy-y2)÷4xy
=4xy÷4xy
=1.
1
8.(2024·汕尾陆河质检)计算:(2y-x)(x-y)+(2x3y+4xy3)÷2xy.
【解析】原式=2xy-2y2-x2+xy+x2+2y2
=3xy.
9.计算4a·3a2b÷2ab的结果是( )
A.6a B.6ab C.6a2 D.6a2b2
【解析】4a·3a2b÷2ab=12a3b÷2ab=6a2.
C
10.(2024·连州市期末)若长方形的面积是8a3+12a2-4ab,其中一边长是4a,则它的邻边
长是( )
A.2a3+3a2-b B.2a2+3a+b
C.3a2+2a+b D.2a2+3a-b
【解析】由题意得:(8a3+12a2-4ab)÷4a=8a3÷4a+12a2÷4a-4ab÷4a=2a2+3a-b,
所以长方形的邻边长是2a2+3a-b,
所以A,B,C选项均不符合题意,D选项符合题意.
D
11.某兴趣小组的门锁密码被设计成如表所示的数学问题,正确的密码是_________.
[x19y8z8]=1 988
[x2yz·x3y]=521
[(x5)5y4z6÷x5y2z]=密码
【解析】因为[(x5)5y4z6÷x5y2z]=[x25y4z6÷x5y2z]=[x20y2z5],
已知:x,y,z的指数是密码,
所以密码为2 025.
2 025
12.先化简,再求值:(2m+3)(2m-3)-(m-1)2+(2m)3÷(-8m),其中m满足m2+m-2=0.
【解析】原式=4m2-9-(m2-2m+1)+8m3÷(-8m)=4m2-9-m2+2m-1-m2=2m2+2m-10= 2(m2+m)-10,
因为m2+m-2=0,所以m2+m=2,
所以原式=2×2-10=-6.
13.(2024·佛山禅城质检)观察下列式子:
(x2-1)÷(x-1)=x+1
(x3-1)÷(x-1)=x2+x+1
(x4-1)÷(x-1)=x3+x2+x+1
(x5-1)÷(x-1)=x4+x3+x2+x+1
(1)根据以上式子,请直接写出(x6-1)÷(x-1)= ;
(2)根据以上式子,请直接写出(xn-1)÷(x-1)的结果 (n为正整数);
(3)计算:1+2+22+23+24+…+22 015.
4 整式的除法
课时目标 素养达成
1.理解单项式除以单项式、多项式除以单项式的运算法则 运算能力、应用意识
2.会进行单项式除以单项式、多项式除以单项式的整式除法运算 抽象能力、推理能力
1.计算6x3÷3x2的结果是( )
A.x B.2x C.2x5 D.2x6
2.计算(25x2y-5xy2)÷5xy的结果等于( )
A.-5x+y B.5x-y
C.-5x+1 D.-5x-1
3.计算:(-9x2+3x)÷(-3x)=_________.
B
B
3x-1
单项式除以单项式(运算能力)
【典例1】(教材再开发·P27例补充)计算:
(1)(2024·广州白云期中)(-2x2y3)3÷(-x2)2.
(2)7.2×1012÷(-3.6×109).
【自主解答】(1)原式=-8x6y9÷x4=-8x2y9.
(2)原式=[7.2÷(-3.6)]×(1012÷109)=-2×103.
1.(2024·深圳龙华质检)25x2y3÷(-5xy)的运算结果是( )
A.-5x2y B.5xy2
C.5x2y D.-5xy2
【解析】25x2y3÷(-5xy)=-5xy2.
D
2.(2024·珠海十一中一模)计算:8x3y÷(2x)2=________.
【解析】原式=8x3y÷4x2=2xy.
2xy
多项式除以单项式(运算能力)
【典例2】(教材再开发·P28习题T1补充)计算:
(1)(2024·河源龙川期末)[(2a)2-4ab+2a]÷2a.
(2)计算:(12m4n-9m2n2+3m3)÷(-3m2).
【自主解答】(1)原式=(4a2-4ab+2a)÷2a=2a-2b+1.
(2)原式=12m4n÷(-3m2)-9m2n2÷(-3m2)+3m3÷(-3m2)=-4m2n+3n2-m.
1.(2024·茂名电白期中)(10x2y-5xy2)÷(-5xy)的结果是( )
A.2x+y B.2x-y
C.-2x-y D.-2x+y
【解析】(10x2y-5xy2)÷(-5xy)
=10x2y÷(-5xy)-5xy2÷(-5xy)
=-2x+y.
D
2.一个长方形的面积是xy2-x2y,若长为xy,那么宽为( )
A.x-y B.y-x
C.x+y D.-x-y
【解析】长方形的宽为:(xy2-x2y)÷xy
=xy2÷xy-x2y÷xy
=y-x.
B
1.(2024·佛山顺德质检)计算(-4x3+2x)÷2x的结果正确的是( )
A.-8x4+4x2 B.-4x3
C.-2x D.-2x2+1
【解析】(-4x3+2x)÷2x=-2x2+1.
D
3.计算:
(1)(2024·深圳南山质检)(-3xy2)2·(-6x2y)÷(9x4y5).
(2)[(3a-b)2+(a+b)(a-b)]÷2a.
【解析】(1)原式=9x2y4·(-6x2y)÷(9x4y5)
=-54x4y5÷(9x4y5)
=-6.
(2)原式=(9a2-6ab+b2+a2-b2)÷2a
=(10a2-6ab)÷2a
=5a-3b.
知识点1 单项式除以单项式
1.计算-14x3y3÷7x2y的结果是( )
A.2x B.-2x C.2y2 D.-2xy2
【解析】原式=[(-14)÷7]·(x3÷x2)·(y3÷y)=-2xy2.
D
2.已知28a3bm÷(28anb2)=b2,那么m,n的值分别为( )
A.4,3 B.4,1 C.1,3 D.2,3
A
知识点2 多项式除以单项式
3.计算(x3-2x2y)÷(-x2)的结果是( )
A.x-2y B.-x+2y
C.-x-2 D.-x+2
【解析】原式=x3÷(-x2)-2x2y÷(-x2)=-x+2y.
B
4.(2024·清远英德期中)计算:(9a3b2-3ab)÷3ab=__________.
【解析】原式=9a3b2÷3ab-3ab÷3ab=3a2b-1.
3a2b-1
5.计算:(12m4n-9m2n2+3m3)÷(-3m2).
【解析】(12m4n-9m2n2+3m3)÷(-3m2)=12m4n÷(-3m2)-9m2n2÷(-3m2)+3m3÷(-3m2)
=-4m2n+3n2-m.
知识点3 整式的混合运算
6.计算[(-a2)3-3a2(-a2)]÷(-a)2的结果是( )
A.-a3+3a2 B.a3-3a2
C.-a4+3a2 D.-a4+a2
【解析】原式=(-a6+3a4)÷a2=-a4+3a2.
C
7.[(x+y)2-(x-y)2]÷4xy=______.
【解析】[(x+y)2-(x-y)2]÷4xy
=[x2+2xy+y2-(x2-2xy+y2)]÷4xy
=(x2+2xy+y2-x2+2xy-y2)÷4xy
=4xy÷4xy
=1.
1
8.(2024·汕尾陆河质检)计算:(2y-x)(x-y)+(2x3y+4xy3)÷2xy.
【解析】原式=2xy-2y2-x2+xy+x2+2y2
=3xy.
9.计算4a·3a2b÷2ab的结果是( )
A.6a B.6ab C.6a2 D.6a2b2
【解析】4a·3a2b÷2ab=12a3b÷2ab=6a2.
C
10.(2024·连州市期末)若长方形的面积是8a3+12a2-4ab,其中一边长是4a,则它的邻边
长是( )
A.2a3+3a2-b B.2a2+3a+b
C.3a2+2a+b D.2a2+3a-b
【解析】由题意得:(8a3+12a2-4ab)÷4a=8a3÷4a+12a2÷4a-4ab÷4a=2a2+3a-b,
所以长方形的邻边长是2a2+3a-b,
所以A,B,C选项均不符合题意,D选项符合题意.
D
11.某兴趣小组的门锁密码被设计成如表所示的数学问题,正确的密码是_________.
[x19y8z8]=1 988
[x2yz·x3y]=521
[(x5)5y4z6÷x5y2z]=密码
【解析】因为[(x5)5y4z6÷x5y2z]=[x25y4z6÷x5y2z]=[x20y2z5],
已知:x,y,z的指数是密码,
所以密码为2 025.
2 025
12.先化简,再求值:(2m+3)(2m-3)-(m-1)2+(2m)3÷(-8m),其中m满足m2+m-2=0.
【解析】原式=4m2-9-(m2-2m+1)+8m3÷(-8m)=4m2-9-m2+2m-1-m2=2m2+2m-10= 2(m2+m)-10,
因为m2+m-2=0,所以m2+m=2,
所以原式=2×2-10=-6.
13.(2024·佛山禅城质检)观察下列式子:
(x2-1)÷(x-1)=x+1
(x3-1)÷(x-1)=x2+x+1
(x4-1)÷(x-1)=x3+x2+x+1
(x5-1)÷(x-1)=x4+x3+x2+x+1
(1)根据以上式子,请直接写出(x6-1)÷(x-1)= ;
(2)根据以上式子,请直接写出(xn-1)÷(x-1)的结果 (n为正整数);
(3)计算:1+2+22+23+24+…+22 015.
同课章节目录
