1.3.3乘法公式第3课时 课件(共28张PPT)
文档属性
| 名称 | 1.3.3乘法公式第3课时 课件(共28张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 930.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 17:07:57 | ||
图片预览







文档简介
(共28张PPT)
3 乘法公式
第3课时
课时目标 素养达成
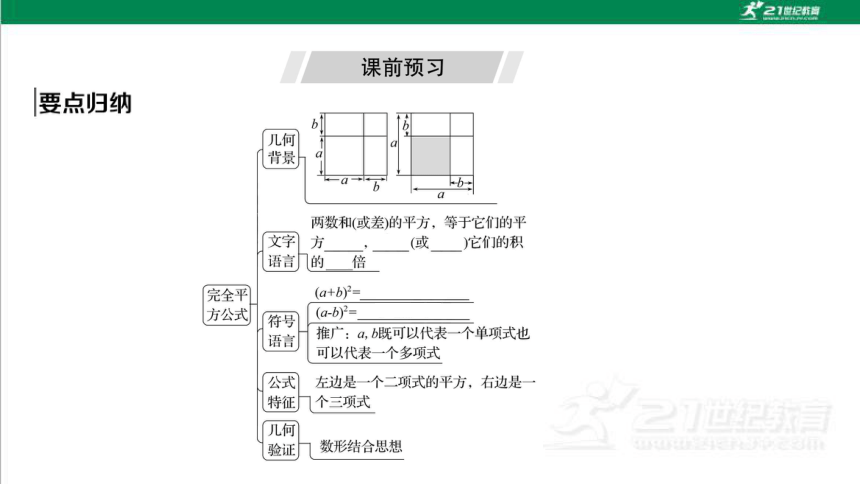
1.理解完全平方公式的推导过程,了解完全平方公式的几何背景 几何直观、抽象能力
2.理解完全平方公式的本质,并会运用完全平方公式进行简单的计算 运算能力
1.计算:(2x-1)2等于( )
A.4x2+1 B.4x2-2x+1
C.4x2-4x-1 D.4x2-4x+1
2.若(x-2)2=x2+mx+n,则m,n的值分别是( )
A.4,4 B.-4,4
C.-4,-4 D.4,-4
D
B
3.运用完全平方公式计算:
(1)(4m+n)2. (2)(-a+b)2.
【解析】(1)(4m+n)2=16m2+8mn+n2.
(2)(-a+b)2=a2-2ab+b2.
完全平方公式的几何背景(几何直观、推理能力)
【典例1】(教材再开发·P20“思考·交流”强化)如图所示,分别以长方形ABCD的BC,CD为边向外作正方形BEFC和正方形DCGH,延长EF,HG交于点I.若正方形BEFC和正方形DCGH的面积和为13,长方形ABCD的面积为6,则正方形AEIH的周长为 .
【自主解答】设正方形BEFC的边长为a,正方形DCGH的边长为b,
因为正方形BEFC和正方形DCGH的面积和为13,长方形ABCD的面积为6,
所以a2+b2=13,ab=6,
又因为(a+b)2=a2+b2+2ab=13+2×6=25,所以a+b=5或a+b=-5(舍去),
所以4(a+b)=20,
即正方形AEIH的周长为20.
答案:20
(2024·深圳期中)[阅读材料]
我们知道,图形也是一种重要的数学语言,它直观形象,能有效地表现一些代数中的数量关系,而运用代数思想也能巧妙地解决一些图形问题.
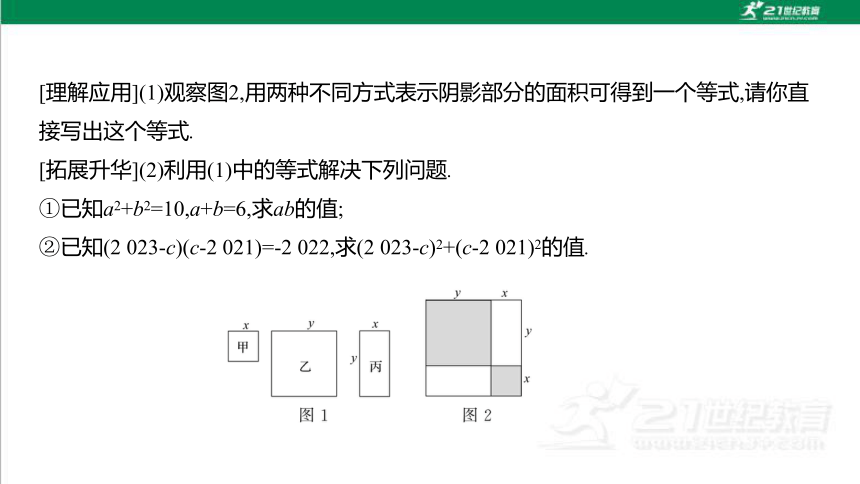
在一次数学活动课上,张老师准备了若干张如图1所示的甲、乙、丙三种纸片,其中甲种纸片是边长为x的正方形,乙种纸片是边长为y的正方形,丙种纸片是长为y,宽为x的长方形.并用甲种纸片一张,乙种纸片一张,丙种纸片两张拼成了如图2所示的一个大正方形.
[理解应用](1)观察图2,用两种不同方式表示阴影部分的面积可得到一个等式,请你直接写出这个等式.
[拓展升华](2)利用(1)中的等式解决下列问题.
①已知a2+b2=10,a+b=6,求ab的值;
②已知(2 023-c)(c-2 021)=-2 022,求(2 023-c)2+(c-2 021)2的值.
【解析】(1)题图2中阴影部分的面积=(x+y)2-2xy,
题图2中阴影部分的面积=x2+y2,
所以(x+y)2-2xy=x2+y2.
(2)①当a2+b2=10,a+b=6时,代入(1)中的等式,得36-2ab=10,解得ab=13.
②因为(2 023-c)(c-2 021)=-2 022,
且(2 023-c)+(c-2 021)=2,
根据(1)中的等式,得4-2×(-2 022)=(2 023-c)2+(c-2 021)2,
所以(2 023-c)2+(c-2 021)2=4 048.
1.(2024·广州白云期中)计算(x-1)2=( )
A.x2-1 B.x2-x+1
C.x2-2x+1 D.x2+2x+1
【解析】(x-1)2=x2-2x+1.
C
2.(2024·佛山顺德期末)计算:(3x-y)2=______________.
【解析】(3x-y)2=9x2-6xy+y2.
9x2-6xy+y2
1.下列运算结果正确的是( )
A.2a+3a=5a2 B.(-ab2)3=-a3b6
C.a3·a3=a9 D.(a+2b)2=a2+4b2
【解析】A.2a+3a=5a,原计算错误,故此选项不符合题意.
B.(-ab2)3=-a3b6,原计算正确,故此选项符合题意.
C.a3·a3=a6,原计算错误,故此选项不符合题意.
D.(a+2b)2=a2+4ab+4b2,原计算错误,故此选项不符合题意.
B
2.计算:(-x-3y)2=______________.
【解析】(-x-3y)2=[-(x+3y)]2=(x+3y)2=x2+9y2+6xy.
x2+9y2+6xy
3.计算:(1)(3a-2b)2. (2)(-x2-y)2.
【解析】(1)原式=(3a)2-2×3a×2b+(2b)2=9a2-12ab+4b2.
(2)原式=x4+2x2y+y2.
知识点1 完全平方公式的几何背景
1.(2024·深圳龙华期末)下列图形阴影部分的面积能够直观地解释(x-1)2=x2-2x+1的是
( )
【解析】选项A中的阴影部分的面积可以用(x-1)2=x2-2x+1来解释.
A
知识点2 完全平方公式的应用
2.下列计算结果正确的是( )
A.(x+y)2=x2+y2
B.(x-y)2=x2-2xy-y2
C.(x+2y)(x-2y)=x2-2y2
D.(3x+y)2=9x2+6xy+y2
【解析】A.原式=x2+y2+2xy,错误;
B.原式=x2-2xy+y2,错误;
C.原式=x2-4y2,错误;
D.原式=9x2+6xy+y2,正确.
D
3.若4x2+4x+m=(2x+1)2,则m的值为( )
A.4 B.1 C.-1 D.-4
【解析】(2x+1)2=4x2+4x+1,所以m=1.
B
4.(2024·深圳福田质检)若(x+2)2=x2+kx+4,则k的值为______.
【解析】(x+2)2=x2+4x+4,则k=4.
4
6.(2024·梅州五华期末)已知(a+b)2=14,ab=3,则a2+b2=( )
A.4 B.8 C.11 D.20
【解析】因为a2+b2=(a+b)2-2ab,(a+b)2=14,ab=3,所以a2+b2=14-2×3=8.
B
7.如图所示,四个等腰直角三角形拼成一个正方形,则阴影部分的面积为( )
A.a2+b2
B.a2-b2
C.2ab
D.4ab
【解析】整体是边长为a+b的正方形,因此面积为(a+b)2,四个等腰直角三角形的面积和为a2+b2,所以阴影部分的面积为(a+b)2-a2-b2=2ab.
C
8.若(x+2y)2=(x-2y)2+A,则代数式A为________.
【解析】因为(x+2y)2=(x-2y)2+A,
所以A=(x+2y)2-(x-2y)2=(x+2y+x-2y)(x+2y-x+2y)=2x·4y=8xy.
8xy
9.已知实数a,b满足a-b=2,则2a2-4ab+2b2的值为______.
【解析】因为a-b=2,所以(a-b)2=a2-2ab+b2=4,所以2a2-4ab+2b2=2(a2-2ab+b2)=2×4=8.
8
11.(2024·珠海金湾期末)【综合探究】实践:把一张长方形纸片进行两次连续对折后得到边长为a,b(a>b)的小长方形(图1),再展开还原(图2)沿着折痕(虚线部分)剪开,拼成一个大正方形(图3).
(1)猜想:①图3中间小正方形的边长为 ;(用含a,b的式子表示)
②根据材料,直接写出式子ab,(a-b)2,(a+b)2之间的等量关系 ;
(2)应用:若x+y=7,xy=2,求(x-y)2的值.
【解析】(1)①由题图3可得中间小正方形的边长为a-b.
答案:a-b
②题图3大正方形的面积可以表示为(a+b)2,还可以表示为小正方形的面积加上4个长方形的面积,4ab+(a-b)2,
所以4ab+(a-b)2=(a+b)2.
答案:4ab+(a-b)2=(a+b)2
(2)由(1)可得4xy+(x-y)2=(x+y)2,
因为x+y=7,xy=2,
所以8+(x-y)2=49,
所以(x-y)2=41.
3 乘法公式
第3课时
课时目标 素养达成
1.理解完全平方公式的推导过程,了解完全平方公式的几何背景 几何直观、抽象能力
2.理解完全平方公式的本质,并会运用完全平方公式进行简单的计算 运算能力
1.计算:(2x-1)2等于( )
A.4x2+1 B.4x2-2x+1
C.4x2-4x-1 D.4x2-4x+1
2.若(x-2)2=x2+mx+n,则m,n的值分别是( )
A.4,4 B.-4,4
C.-4,-4 D.4,-4
D
B
3.运用完全平方公式计算:
(1)(4m+n)2. (2)(-a+b)2.
【解析】(1)(4m+n)2=16m2+8mn+n2.
(2)(-a+b)2=a2-2ab+b2.
完全平方公式的几何背景(几何直观、推理能力)
【典例1】(教材再开发·P20“思考·交流”强化)如图所示,分别以长方形ABCD的BC,CD为边向外作正方形BEFC和正方形DCGH,延长EF,HG交于点I.若正方形BEFC和正方形DCGH的面积和为13,长方形ABCD的面积为6,则正方形AEIH的周长为 .
【自主解答】设正方形BEFC的边长为a,正方形DCGH的边长为b,
因为正方形BEFC和正方形DCGH的面积和为13,长方形ABCD的面积为6,
所以a2+b2=13,ab=6,
又因为(a+b)2=a2+b2+2ab=13+2×6=25,所以a+b=5或a+b=-5(舍去),
所以4(a+b)=20,
即正方形AEIH的周长为20.
答案:20
(2024·深圳期中)[阅读材料]
我们知道,图形也是一种重要的数学语言,它直观形象,能有效地表现一些代数中的数量关系,而运用代数思想也能巧妙地解决一些图形问题.
在一次数学活动课上,张老师准备了若干张如图1所示的甲、乙、丙三种纸片,其中甲种纸片是边长为x的正方形,乙种纸片是边长为y的正方形,丙种纸片是长为y,宽为x的长方形.并用甲种纸片一张,乙种纸片一张,丙种纸片两张拼成了如图2所示的一个大正方形.
[理解应用](1)观察图2,用两种不同方式表示阴影部分的面积可得到一个等式,请你直接写出这个等式.
[拓展升华](2)利用(1)中的等式解决下列问题.
①已知a2+b2=10,a+b=6,求ab的值;
②已知(2 023-c)(c-2 021)=-2 022,求(2 023-c)2+(c-2 021)2的值.
【解析】(1)题图2中阴影部分的面积=(x+y)2-2xy,
题图2中阴影部分的面积=x2+y2,
所以(x+y)2-2xy=x2+y2.
(2)①当a2+b2=10,a+b=6时,代入(1)中的等式,得36-2ab=10,解得ab=13.
②因为(2 023-c)(c-2 021)=-2 022,
且(2 023-c)+(c-2 021)=2,
根据(1)中的等式,得4-2×(-2 022)=(2 023-c)2+(c-2 021)2,
所以(2 023-c)2+(c-2 021)2=4 048.
1.(2024·广州白云期中)计算(x-1)2=( )
A.x2-1 B.x2-x+1
C.x2-2x+1 D.x2+2x+1
【解析】(x-1)2=x2-2x+1.
C
2.(2024·佛山顺德期末)计算:(3x-y)2=______________.
【解析】(3x-y)2=9x2-6xy+y2.
9x2-6xy+y2
1.下列运算结果正确的是( )
A.2a+3a=5a2 B.(-ab2)3=-a3b6
C.a3·a3=a9 D.(a+2b)2=a2+4b2
【解析】A.2a+3a=5a,原计算错误,故此选项不符合题意.
B.(-ab2)3=-a3b6,原计算正确,故此选项符合题意.
C.a3·a3=a6,原计算错误,故此选项不符合题意.
D.(a+2b)2=a2+4ab+4b2,原计算错误,故此选项不符合题意.
B
2.计算:(-x-3y)2=______________.
【解析】(-x-3y)2=[-(x+3y)]2=(x+3y)2=x2+9y2+6xy.
x2+9y2+6xy
3.计算:(1)(3a-2b)2. (2)(-x2-y)2.
【解析】(1)原式=(3a)2-2×3a×2b+(2b)2=9a2-12ab+4b2.
(2)原式=x4+2x2y+y2.
知识点1 完全平方公式的几何背景
1.(2024·深圳龙华期末)下列图形阴影部分的面积能够直观地解释(x-1)2=x2-2x+1的是
( )
【解析】选项A中的阴影部分的面积可以用(x-1)2=x2-2x+1来解释.
A
知识点2 完全平方公式的应用
2.下列计算结果正确的是( )
A.(x+y)2=x2+y2
B.(x-y)2=x2-2xy-y2
C.(x+2y)(x-2y)=x2-2y2
D.(3x+y)2=9x2+6xy+y2
【解析】A.原式=x2+y2+2xy,错误;
B.原式=x2-2xy+y2,错误;
C.原式=x2-4y2,错误;
D.原式=9x2+6xy+y2,正确.
D
3.若4x2+4x+m=(2x+1)2,则m的值为( )
A.4 B.1 C.-1 D.-4
【解析】(2x+1)2=4x2+4x+1,所以m=1.
B
4.(2024·深圳福田质检)若(x+2)2=x2+kx+4,则k的值为______.
【解析】(x+2)2=x2+4x+4,则k=4.
4
6.(2024·梅州五华期末)已知(a+b)2=14,ab=3,则a2+b2=( )
A.4 B.8 C.11 D.20
【解析】因为a2+b2=(a+b)2-2ab,(a+b)2=14,ab=3,所以a2+b2=14-2×3=8.
B
7.如图所示,四个等腰直角三角形拼成一个正方形,则阴影部分的面积为( )
A.a2+b2
B.a2-b2
C.2ab
D.4ab
【解析】整体是边长为a+b的正方形,因此面积为(a+b)2,四个等腰直角三角形的面积和为a2+b2,所以阴影部分的面积为(a+b)2-a2-b2=2ab.
C
8.若(x+2y)2=(x-2y)2+A,则代数式A为________.
【解析】因为(x+2y)2=(x-2y)2+A,
所以A=(x+2y)2-(x-2y)2=(x+2y+x-2y)(x+2y-x+2y)=2x·4y=8xy.
8xy
9.已知实数a,b满足a-b=2,则2a2-4ab+2b2的值为______.
【解析】因为a-b=2,所以(a-b)2=a2-2ab+b2=4,所以2a2-4ab+2b2=2(a2-2ab+b2)=2×4=8.
8
11.(2024·珠海金湾期末)【综合探究】实践:把一张长方形纸片进行两次连续对折后得到边长为a,b(a>b)的小长方形(图1),再展开还原(图2)沿着折痕(虚线部分)剪开,拼成一个大正方形(图3).
(1)猜想:①图3中间小正方形的边长为 ;(用含a,b的式子表示)
②根据材料,直接写出式子ab,(a-b)2,(a+b)2之间的等量关系 ;
(2)应用:若x+y=7,xy=2,求(x-y)2的值.
【解析】(1)①由题图3可得中间小正方形的边长为a-b.
答案:a-b
②题图3大正方形的面积可以表示为(a+b)2,还可以表示为小正方形的面积加上4个长方形的面积,4ab+(a-b)2,
所以4ab+(a-b)2=(a+b)2.
答案:4ab+(a-b)2=(a+b)2
(2)由(1)可得4xy+(x-y)2=(x+y)2,
因为x+y=7,xy=2,
所以8+(x-y)2=49,
所以(x-y)2=41.
同课章节目录
