7.1.3 两条直线被第三条直线所截 课件(共35张PPT)
文档属性
| 名称 | 7.1.3 两条直线被第三条直线所截 课件(共35张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 578.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 21:20:47 | ||
图片预览






文档简介
(共35张PPT)
7.1.3 两条直线被第三条直线所截
课时目标 素养达成
1.理解同位角、内错角、同旁内角的概念 模型观念、几何直观
2.识别同位角、内错角、同旁内角 几何直观、推理能力
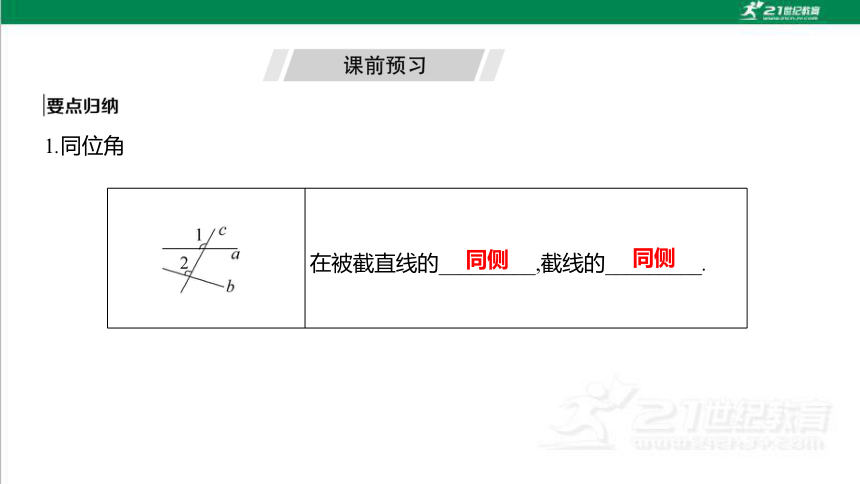
1.同位角
在被截直线的_________,截线的_________.
同侧
同侧
2.内错角
在被截直线的_________,截线的_________.
内侧
两侧
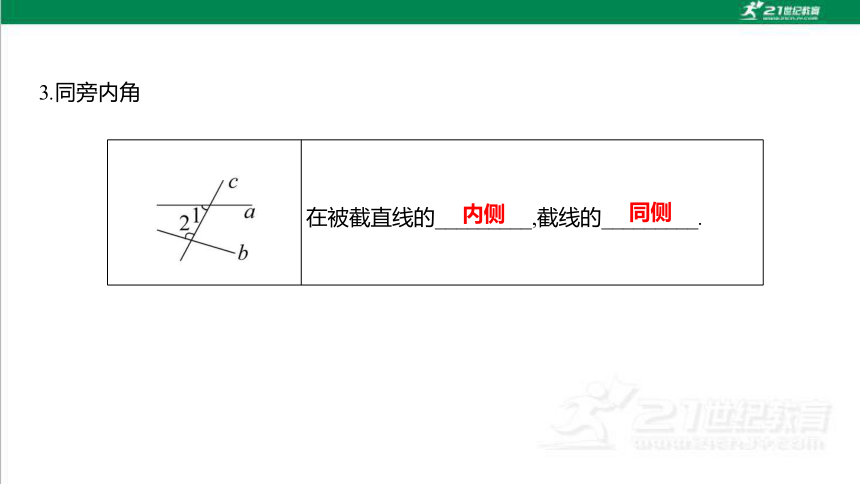
3.同旁内角
在被截直线的_________,截线的_________.
内侧
同侧
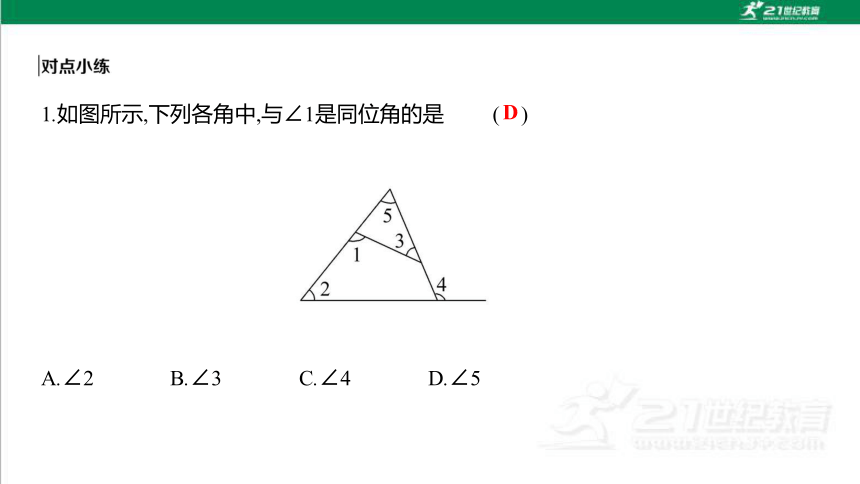
1.如图所示,下列各角中,与∠1是同位角的是 ( )
A.∠2 B.∠3 C.∠4 D.∠5
D
2.如图所示,在不添加任何线的情况下,图中一定存在 ( )
A.同位角 B.内错角
C.同旁内角 D.以上角都不存在
B
3.如图所示,∠3的同旁内角是 ( )
A.∠1 B.∠2
C.∠4 D.∠1和∠4
D
【典例】(教材再开发· P7例3变式)如图所示,在直角三角形ABC中,∠C=90°,DE⊥AC交AC于点E,交AB于点D.
请分别写出当BC,DE被AB所截时,∠B的同位角、内错角和同旁内角.
【自主解答】当BC,DE被AB所截时,∠B的同位角为∠1;∠B的内错角为∠2;∠B的同旁内角为∠BDE.
同位角、内错角、同旁内角的识别(模型观念)
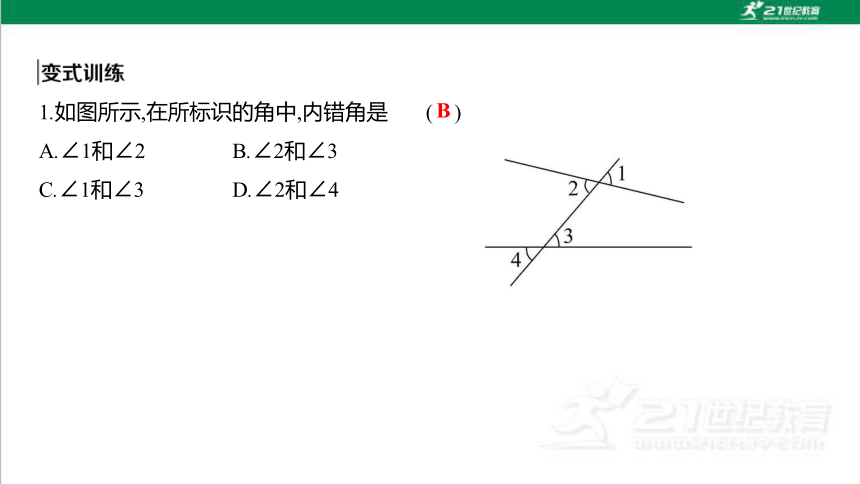
1.如图所示,在所标识的角中,内错角是 ( )
A.∠1和∠2 B.∠2和∠3
C.∠1和∠3 D.∠2和∠4
B
【解析】A.∠1和∠2是对顶角;
B.∠2和∠3是内错角;
C.∠1和∠3是同位角;
D.∠2和∠4是同位角.
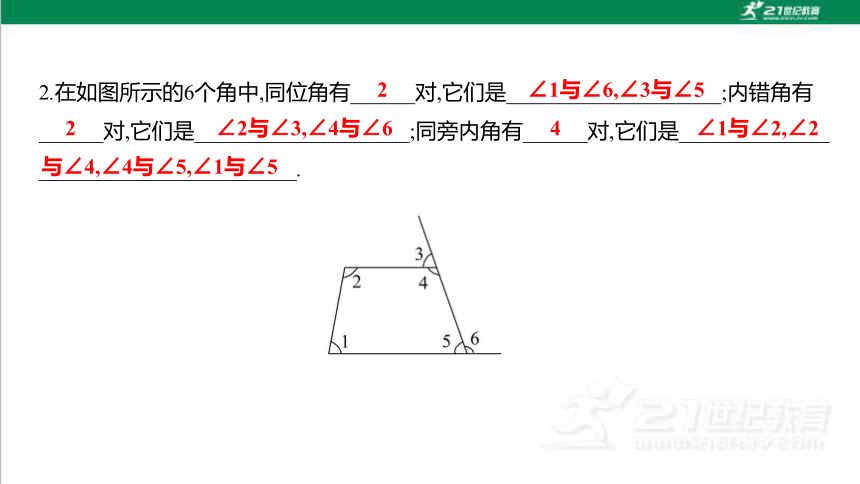
2.在如图所示的6个角中,同位角有______对,它们是____________________;内错角有
______对,它们是____________________;同旁内角有______对,它们是______________
________________________.
2
∠1与∠6,∠3与∠5
2
∠2与∠3,∠4与∠6
4
∠1与∠2,∠2
与∠4,∠4与∠5,∠1与∠5
【解析】在题图所示的6个角中,同位角有2对,它们是∠1与∠6,∠3与∠5;内错角有
2对,它们是∠2与∠3,∠4与∠6;同旁内角有4对,它们是∠1与∠2,∠2与∠4,∠4与
∠5,∠1与∠5.
1.(2024·深圳宝安质检)下列图中∠1,∠2不是同位角的是 ( )
D
【解析】由同位角定义知,A,B,C选项图中的∠1和∠2是同位角,D项中的∠1和∠2不是同位角.
2.如图所示,两只手的食指和拇指在同一平面内,它们构成的一对角可以看成 ( )
A.同位角 B.同旁内角
C.内错角 D.对顶角
B
【解析】两只手的食指和拇指在同一个平面内,两个拇指所在的两条直线被两个食指所在的直线所截,并且形成的两角位于两直线之间且在截线同侧,因而构成的一对角可看成是同旁内角.
3.如图所示,图中用数字标出的角中,∠2的内错角是________.
∠6
【解析】题图中用数字标出的角中,∠2的内错角是∠6.
4.如图所示,∠1与∠2是直线________与________被直线________所截而成的内错角.
【解析】∠1与∠2是直线AB与CD被直线AC所截而成的内错角.
AB
CD
AC
5.(1)指出下列各图中的∠1与∠2是同位角、内错角还是同旁内角.
①________;②________;③________;④________.
(2)请你归纳:辨认同位角、内错角、同旁内角的方法可以是什么
【解析】(1)①∠1与∠2是内错角;②∠1与∠2是同旁内角;③∠1与∠2是同位角;
④∠1与∠2是同位角.
答案:①内错角 ②同旁内角
③同位角 ④同位角
(2)辨认同位角、内错角、同旁内角的方法:可通过同位角的边构成“F”形,内错角的边构成“Z”形,同旁内角的边构成“U”形进行判断.
知识点1 同位角、内错角、同旁内角的识别
1.(2024·河源连平期末)如图所示,与∠1成同位角的角共有 ( )
A.1个 B.2个 C.3个 D.4个
C
【解析】与∠1成同位角的角有∠DAB,∠EBH,∠FGH,共3个.
2.如图所示,∠1的内错角是 ( )
A.∠2 B.∠3 C.∠4 D.∠5
【解析】根据内错角的定义可得:∠1的内错角是∠3.
B
3.判断:(在横线上填入“正确”或“错误”)
(1)图中,∠D与∠5是同位角_________;∠D与∠ACE是同位角_________.
(2)图中,∠1与∠5是内错角_________;∠2与∠4是内错角_________.
(3)图中,∠B与∠D是同旁内角_________;∠2与∠3是同旁内角_________.
正确
正确
错误
正确
错误
正确
【解析】(1)∠D与∠5是同位角,∠D与∠ACE是同位角.
答案:正确 正确
(2)∠1与∠5不是内错角,∠2与∠4是内错角.
答案:错误 正确
(3)∠B与∠D不是同旁内角,∠2与∠3是同旁内角.
答案:错误 正确
知识点2 同位角、内错角、同旁内角的应用
4.两条直线被第三条直线所截,∠1是∠2的同旁内角,∠2是∠3的内错角.
(1)画出示意图,标出∠1,∠2,∠3;
(2)若∠1=2∠2,∠2=2∠3,求∠1,∠2,∠3的度数.
【解析】(1)如图所示.
(2)∵∠1=2∠2,∠2=2∠3,∴设∠3=x,
则∠2=2x,∠1=4x,
∵∠1+∠3=180°,
∴4x+x=180°,解得x=36°,
故∠3=36°,∠2=72°,∠1=144°.
5.如图所示,下列说法中,不正确的是 ( )
A.∠5和∠4是同位角
B.∠1和∠5是内错角
C.∠2和∠3是同位角
D.∠1和∠2是同旁内角
C
【解析】A.∠5与∠4是直线l1,直线l2,被直线l3所截的同位角;
B.∠1与∠5是直线l3,直线l4,被直线l1所截的内错角;
C.∠2与∠3不是两条直线被第三条直线所截得到的角,既不是同位角、内错角,也不是同旁内角;
D.∠1与∠2是直线l3,直线l4,被直线l1所截的同旁内角.
6.如图所示,在∠1,∠2,∠3,∠4,∠5和∠C中,同位角对数为a,内错角对数为b,同旁内角
对数为c,则abc=_______.
16
【解析】同位角:∠1与∠C,∠5与∠C.内错角:∠2与∠4,∠3与∠5.
同旁内角:∠2与∠5,∠3与∠4,∠4与∠C,∠3与∠C.
∴a=2,b=2,c=4,∴abc=2×2×4=16.
7.如图所示,在一个“凹型”图形中,下列说法都正确吗 如果不正确,请加以更正.
(1)∠H与∠A是同旁内角,∠H与∠G是内错角;
(2)与∠D互为同旁内角的角只有∠C;
(3)图中没有同位角.
【解析】(1)∠H与∠A是同旁内角,∠H与∠G是内错角,正确;
(2)与∠D互为同旁内角的角有∠C和∠E,错误;(3)图中没有同位角,正确.
8.(几何直观)下图是一个跳棋棋盘,其游戏规则是:一个棋子从某一个起始角开始,经过若干步跳动以后,到达终点角.跳动时,每一步只能跳到它的同位角或内错角或同旁内角的位置上,例如:从起始位置∠1跳到终点位置∠3写出其中两种不同路径.
路径1:∠1同旁内角∠9内错角∠3.
路径2:∠1内错角∠12内错角∠6同位角∠10同旁内角∠3.
试一试:
(1)从起始角∠1跳到终点角∠8;
(2)从起始角∠1依次按同位角、内错角、同旁内角的顺序跳,能否跳到终点角∠8
【解析】(1)路径:∠1内错角∠12同旁内角∠8.(答案不唯一)
(2)从起始角∠1依次按同位角、内错角、同旁内角的顺序跳,能跳到终点角∠8.
其路径为:∠1同位角∠10内错角∠5同旁内角∠8.
7.1.3 两条直线被第三条直线所截
课时目标 素养达成
1.理解同位角、内错角、同旁内角的概念 模型观念、几何直观
2.识别同位角、内错角、同旁内角 几何直观、推理能力
1.同位角
在被截直线的_________,截线的_________.
同侧
同侧
2.内错角
在被截直线的_________,截线的_________.
内侧
两侧
3.同旁内角
在被截直线的_________,截线的_________.
内侧
同侧
1.如图所示,下列各角中,与∠1是同位角的是 ( )
A.∠2 B.∠3 C.∠4 D.∠5
D
2.如图所示,在不添加任何线的情况下,图中一定存在 ( )
A.同位角 B.内错角
C.同旁内角 D.以上角都不存在
B
3.如图所示,∠3的同旁内角是 ( )
A.∠1 B.∠2
C.∠4 D.∠1和∠4
D
【典例】(教材再开发· P7例3变式)如图所示,在直角三角形ABC中,∠C=90°,DE⊥AC交AC于点E,交AB于点D.
请分别写出当BC,DE被AB所截时,∠B的同位角、内错角和同旁内角.
【自主解答】当BC,DE被AB所截时,∠B的同位角为∠1;∠B的内错角为∠2;∠B的同旁内角为∠BDE.
同位角、内错角、同旁内角的识别(模型观念)
1.如图所示,在所标识的角中,内错角是 ( )
A.∠1和∠2 B.∠2和∠3
C.∠1和∠3 D.∠2和∠4
B
【解析】A.∠1和∠2是对顶角;
B.∠2和∠3是内错角;
C.∠1和∠3是同位角;
D.∠2和∠4是同位角.
2.在如图所示的6个角中,同位角有______对,它们是____________________;内错角有
______对,它们是____________________;同旁内角有______对,它们是______________
________________________.
2
∠1与∠6,∠3与∠5
2
∠2与∠3,∠4与∠6
4
∠1与∠2,∠2
与∠4,∠4与∠5,∠1与∠5
【解析】在题图所示的6个角中,同位角有2对,它们是∠1与∠6,∠3与∠5;内错角有
2对,它们是∠2与∠3,∠4与∠6;同旁内角有4对,它们是∠1与∠2,∠2与∠4,∠4与
∠5,∠1与∠5.
1.(2024·深圳宝安质检)下列图中∠1,∠2不是同位角的是 ( )
D
【解析】由同位角定义知,A,B,C选项图中的∠1和∠2是同位角,D项中的∠1和∠2不是同位角.
2.如图所示,两只手的食指和拇指在同一平面内,它们构成的一对角可以看成 ( )
A.同位角 B.同旁内角
C.内错角 D.对顶角
B
【解析】两只手的食指和拇指在同一个平面内,两个拇指所在的两条直线被两个食指所在的直线所截,并且形成的两角位于两直线之间且在截线同侧,因而构成的一对角可看成是同旁内角.
3.如图所示,图中用数字标出的角中,∠2的内错角是________.
∠6
【解析】题图中用数字标出的角中,∠2的内错角是∠6.
4.如图所示,∠1与∠2是直线________与________被直线________所截而成的内错角.
【解析】∠1与∠2是直线AB与CD被直线AC所截而成的内错角.
AB
CD
AC
5.(1)指出下列各图中的∠1与∠2是同位角、内错角还是同旁内角.
①________;②________;③________;④________.
(2)请你归纳:辨认同位角、内错角、同旁内角的方法可以是什么
【解析】(1)①∠1与∠2是内错角;②∠1与∠2是同旁内角;③∠1与∠2是同位角;
④∠1与∠2是同位角.
答案:①内错角 ②同旁内角
③同位角 ④同位角
(2)辨认同位角、内错角、同旁内角的方法:可通过同位角的边构成“F”形,内错角的边构成“Z”形,同旁内角的边构成“U”形进行判断.
知识点1 同位角、内错角、同旁内角的识别
1.(2024·河源连平期末)如图所示,与∠1成同位角的角共有 ( )
A.1个 B.2个 C.3个 D.4个
C
【解析】与∠1成同位角的角有∠DAB,∠EBH,∠FGH,共3个.
2.如图所示,∠1的内错角是 ( )
A.∠2 B.∠3 C.∠4 D.∠5
【解析】根据内错角的定义可得:∠1的内错角是∠3.
B
3.判断:(在横线上填入“正确”或“错误”)
(1)图中,∠D与∠5是同位角_________;∠D与∠ACE是同位角_________.
(2)图中,∠1与∠5是内错角_________;∠2与∠4是内错角_________.
(3)图中,∠B与∠D是同旁内角_________;∠2与∠3是同旁内角_________.
正确
正确
错误
正确
错误
正确
【解析】(1)∠D与∠5是同位角,∠D与∠ACE是同位角.
答案:正确 正确
(2)∠1与∠5不是内错角,∠2与∠4是内错角.
答案:错误 正确
(3)∠B与∠D不是同旁内角,∠2与∠3是同旁内角.
答案:错误 正确
知识点2 同位角、内错角、同旁内角的应用
4.两条直线被第三条直线所截,∠1是∠2的同旁内角,∠2是∠3的内错角.
(1)画出示意图,标出∠1,∠2,∠3;
(2)若∠1=2∠2,∠2=2∠3,求∠1,∠2,∠3的度数.
【解析】(1)如图所示.
(2)∵∠1=2∠2,∠2=2∠3,∴设∠3=x,
则∠2=2x,∠1=4x,
∵∠1+∠3=180°,
∴4x+x=180°,解得x=36°,
故∠3=36°,∠2=72°,∠1=144°.
5.如图所示,下列说法中,不正确的是 ( )
A.∠5和∠4是同位角
B.∠1和∠5是内错角
C.∠2和∠3是同位角
D.∠1和∠2是同旁内角
C
【解析】A.∠5与∠4是直线l1,直线l2,被直线l3所截的同位角;
B.∠1与∠5是直线l3,直线l4,被直线l1所截的内错角;
C.∠2与∠3不是两条直线被第三条直线所截得到的角,既不是同位角、内错角,也不是同旁内角;
D.∠1与∠2是直线l3,直线l4,被直线l1所截的同旁内角.
6.如图所示,在∠1,∠2,∠3,∠4,∠5和∠C中,同位角对数为a,内错角对数为b,同旁内角
对数为c,则abc=_______.
16
【解析】同位角:∠1与∠C,∠5与∠C.内错角:∠2与∠4,∠3与∠5.
同旁内角:∠2与∠5,∠3与∠4,∠4与∠C,∠3与∠C.
∴a=2,b=2,c=4,∴abc=2×2×4=16.
7.如图所示,在一个“凹型”图形中,下列说法都正确吗 如果不正确,请加以更正.
(1)∠H与∠A是同旁内角,∠H与∠G是内错角;
(2)与∠D互为同旁内角的角只有∠C;
(3)图中没有同位角.
【解析】(1)∠H与∠A是同旁内角,∠H与∠G是内错角,正确;
(2)与∠D互为同旁内角的角有∠C和∠E,错误;(3)图中没有同位角,正确.
8.(几何直观)下图是一个跳棋棋盘,其游戏规则是:一个棋子从某一个起始角开始,经过若干步跳动以后,到达终点角.跳动时,每一步只能跳到它的同位角或内错角或同旁内角的位置上,例如:从起始位置∠1跳到终点位置∠3写出其中两种不同路径.
路径1:∠1同旁内角∠9内错角∠3.
路径2:∠1内错角∠12内错角∠6同位角∠10同旁内角∠3.
试一试:
(1)从起始角∠1跳到终点角∠8;
(2)从起始角∠1依次按同位角、内错角、同旁内角的顺序跳,能否跳到终点角∠8
【解析】(1)路径:∠1内错角∠12同旁内角∠8.(答案不唯一)
(2)从起始角∠1依次按同位角、内错角、同旁内角的顺序跳,能跳到终点角∠8.
其路径为:∠1同位角∠10内错角∠5同旁内角∠8.
同课章节目录
