7.2.2 平行线的判定 课件(共38张PPT)
文档属性
| 名称 | 7.2.2 平行线的判定 课件(共38张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 968.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 21:19:20 | ||
图片预览






文档简介
(共38张PPT)
7.2.2 平行线的判定
课时目标 素养达成
1.经历探索两直线平行条件的过程,理解两直线平
行的条件,会运用条件判定两直线平行 推理能力、模型观念
2.掌握基本事实:两条直线被第三条直线所截,如果
同位角相等,那么这两条直线平行 几何直观、推理能力
3.探索并证明平行线的判定定理:两条直线被第三
条直线所截,如果内错角相等(或同旁内角互补),那
么这两条直线平行 推理能力、模型观念
4.进一步掌握直线平行的条件,并能解决一些简单
的问题.初步了解推理论证的方法,会正确书写简
单的推理过程 推理能力、模型观念
如图所示:两条直线AB,CD被第三条直线EF所截.
1.平行线的判定方法1
文字表述:同位角_________,两直线平行.
几何语言:∵∠1=________,∴AB_______CD.
2.平行线的判定方法2
文字表述:内错角_________,两直线平行.
几何语言:∵∠2=________,
∴AB_______CD.
相等
∠5
∥
相等
∠8
∥
3.平行线的判定方法3
文字表述:同旁内角_________,两直线平行.
几何语言:∵∠2+________=180°,
∴AB_______CD.
4.平行线的其他判定方法
(1)在同一平面内,平行于同一条直线的两条直线_________.
(2)在同一平面内,垂直于同一条直线的两条直线_________.
互补
∠5
∥
平行
平行
1.判断.(正确的画“√”,错误的画“×”)
(1)在同一平面内,a,b,c是直线,且a∥b,b∥c,则a∥c. ( )
(2)在同一平面内,a,b,c是直线,且a⊥b,b⊥c,则a⊥c. ( )
√
×
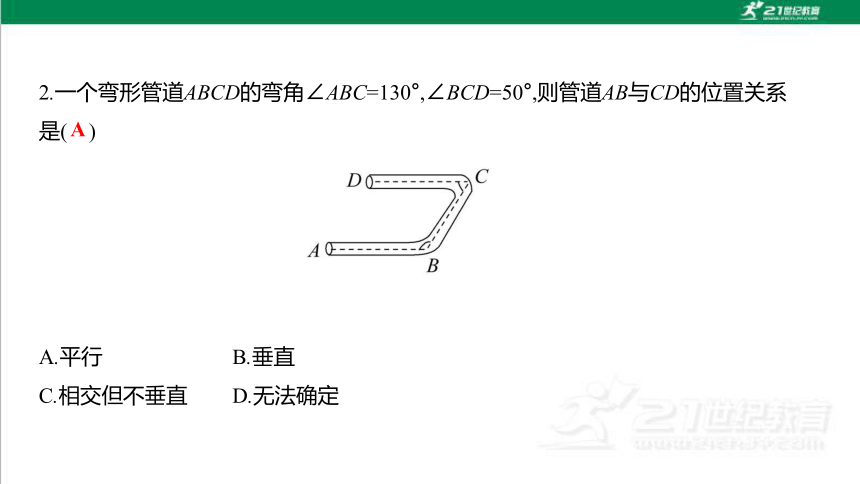
2.一个弯形管道ABCD的弯角∠ABC=130°,∠BCD=50°,则管道AB与CD的位置关系
是( )
A.平行 B.垂直
C.相交但不垂直 D.无法确定
A
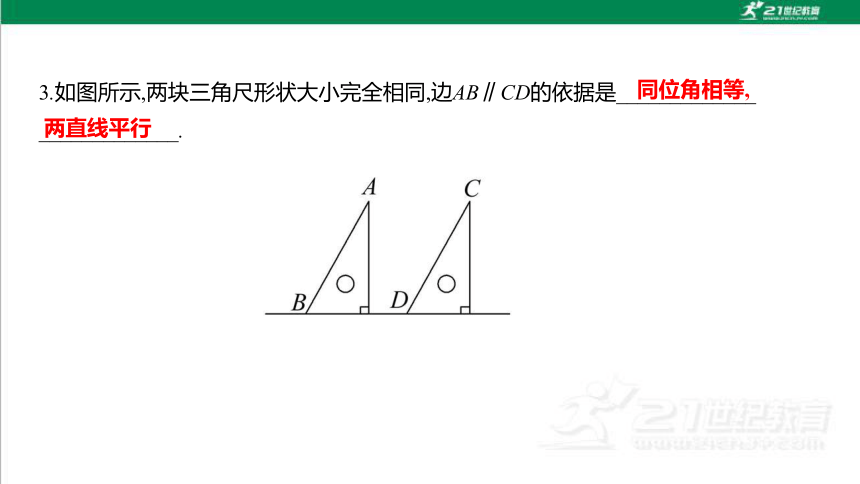
3.如图所示,两块三角尺形状大小完全相同,边AB∥CD的依据是_____________
_____________.
同位角相等,
两直线平行
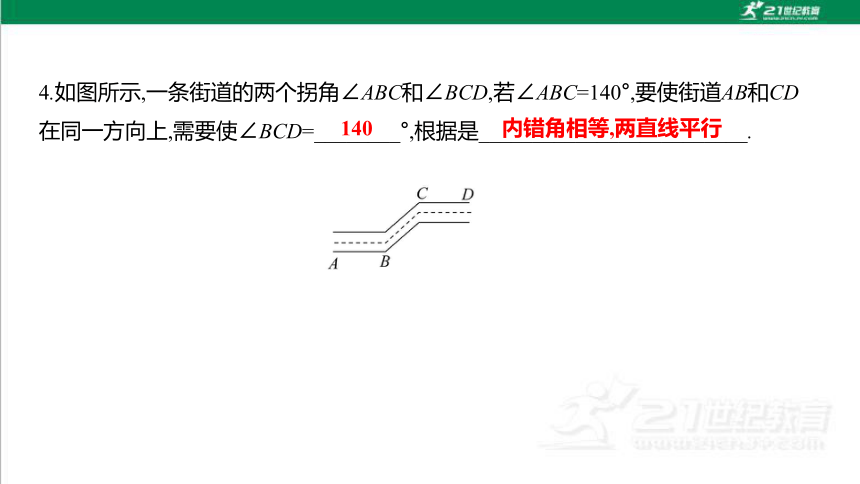
4.如图所示,一条街道的两个拐角∠ABC和∠BCD,若∠ABC=140°,要使街道AB和CD
在同一方向上,需要使∠BCD=________°,根据是_________________________.
140
内错角相等,两直线平行
【典例1】(教材再开发·P14练习T1变式)如图所示,∠1=∠3,∠1+∠2=180°,试说明
CD∥EF.
【自主解答】∵∠1=∠3,
∴AB∥EF.
∵∠4+∠2=180°,∠1+∠2=180°,
∴∠4=∠1,
∴CD∥AB,
∴CD∥EF.
平行线的判定(推理能力)
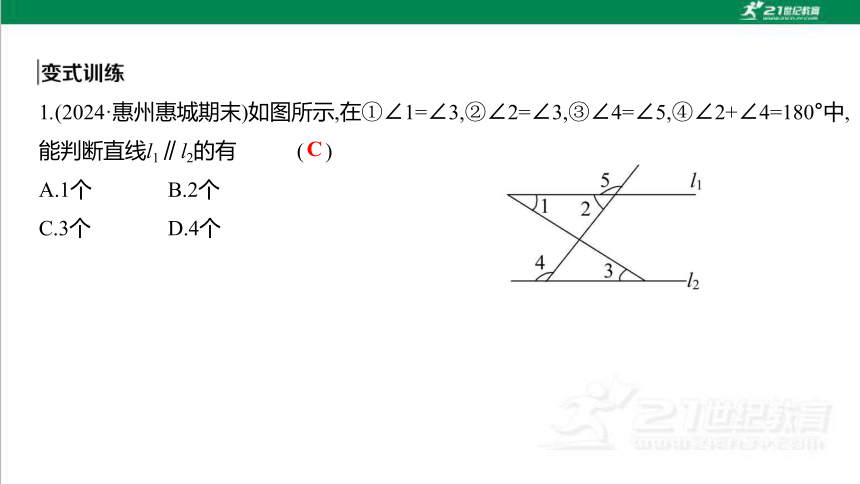
1.(2024·惠州惠城期末)如图所示,在①∠1=∠3,②∠2=∠3,③∠4=∠5,④∠2+∠4=180°中,
能判断直线l1∥l2的有 ( )
A.1个 B.2个
C.3个 D.4个
C
【解析】∵∠1=∠3,
∴l1∥l2(平行线的判定方法2).
∵∠4=∠5,
∴l1∥l2(平行线的判定方法1).
∵∠2+∠4=180°,
∴l1∥l2(平行线的判定方法3).
则能判断直线l1∥l2的有3个.
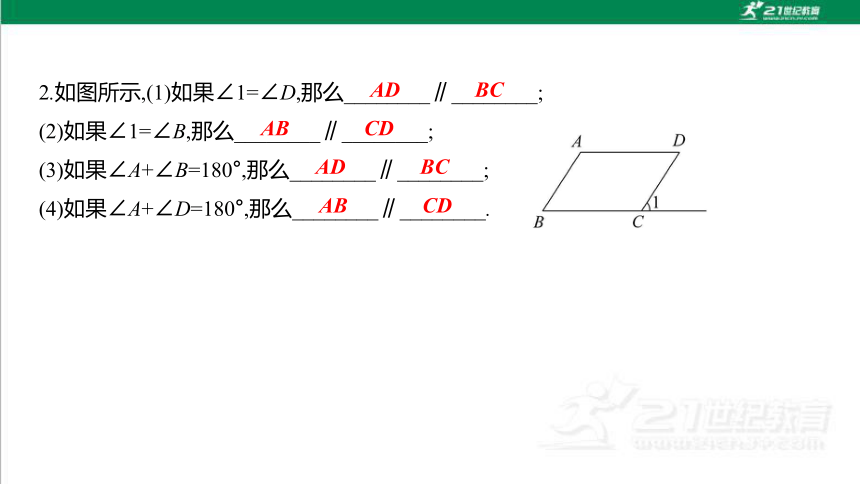
2.如图所示,(1)如果∠1=∠D,那么________∥________;
(2)如果∠1=∠B,那么________∥________;
(3)如果∠A+∠B=180°,那么________∥________;
(4)如果∠A+∠D=180°,那么________∥________.
AD
BC
AB
CD
AD
BC
AB
CD
【解析】(1)如果∠1=∠D,那么AD∥BC(内错角相等,两直线平行).
(2)如果∠1=∠B,那么AB∥CD(同位角相等,两直线平行).
(3)如果∠A+∠B=180°,那么AD∥BC(同旁内角互补,两直线平行).
(4)如果∠A+∠D=180°,那么AB∥CD(同旁内角互补,两直线平行).
【典例2】(教材再开发·P15练习T2变式)如图所示,王师傅将两块相同的长方形木板AB,CD平行放置并间隔一定距离,用长、宽相等的两块铁片a,b分别搭在AB,CD上,再用螺丝固定,做成了一个简易的冰箱底垫.已知∠1=90°,用量角器度量出哪一个角的度数,就可以判断铁片a与b是否平行
【自主解答】用量角器度量出∠3或∠2的度数,就可以判断铁片a与b是否为平行关系.
平行判定的应用(应用意识、推理能力)
1.(2024·韶关乳源期中)下列各图是由含30°角或45°角的直角三角尺组合而成的,其中
利用内错角相等画出AB∥CD的是 ( )
A.图1、图3 B.图2、图4
C.图1、图2、图4 D.图2、图3、图4
B
【解析】观察题图可得,图1由同位角相等,两直线平行,可以画出AB∥CD,故图1不符合题意;
图2∠BAD=∠ADC=30°,由内错角相等,两直线平行,可以画出AB∥CD,故图2符合题意;
图3∠B+∠D=90°+90°=180°,由同旁内角互补,两直线平行,可以画出AB∥CD,故图3不符合题意;
图4∠ABC=∠BCD=90°,由内错角相等,两直线平行,可以画出AB∥CD,故图4符合题意.
综上,利用内错角相等画出AB∥CD的是图2、图4.
2.如图表示钉在一起的木条a,b,c.若测得∠1=50°,∠2=75°,要使木条a∥b,木条a至少要
按图中所示方向旋转_______°.
25
【解析】如图所示,∵当∠2=∠1=50°时,AB∥b,∴要使木条a与b平行,木条a至少要按图中所示方向旋转75°-50°=25°.
1.(2024·佛山顺德期末)如图所示,直线a,b被直线c,d所截,则下列条件可以判定直线
c∥d的是 ( )
A.∠2=∠3
B.∠1=∠3
C.∠1+∠5=180°
D.∠4+∠5=180°
C
【解析】由∠2=∠3,不能判定c∥d,故A不符合题意;
∵∠1=∠3,
∴a∥b,故B不符合题意;
∵∠1+∠5=180°,
∴c∥d,故C符合题意;
∵∠4+∠5=180°,
∴a∥b,故D不符合题意.
2.平面内有两两不重合的直线l1,l2和l,已知l1⊥l,l2⊥l,则l1,l2的位置关系是 ( )
A.互相平行
B.可能平行,可能不平行
C.互相垂直
D.可能垂直,可能不垂直
A
【解析】∵l1⊥l,l2⊥l,∴∠1=∠2=90°,则l1∥l2.
3.如图所示,取一张长方形的硬纸片ABCD对折,MN是折痕,把面ABNM平摊在桌面上,
另一个面CDMN不论怎样改变位置,总有MN∥________∥________.因此________∥
________.
AB
CD
AB
CD
【解析】∵长方形的硬纸片ABCD对折,MN是折痕,
∴MN∥AB,MN∥CD,即MN∥AB∥CD,
∴AB∥CD(平行于同一直线的两条直线互相平行).
知识点1 平行线的判定
1.如图所示,过直线外一点画已知直线的平行线的方法叫“推平行线”法(图中三角形
ABC是三角尺),其依据是 ( )
A.同旁内角互补,两直线平行
B.两直线平行,同旁内角互补
C.同位角相等,两直线平行
D.两直线平行,同位角相等
【解析】∵∠1=∠2,∴a∥b(同位角相等,两直线平行),∴C正确.
C
2.(2024·清远清城期末)如图所示,已知直线EF⊥MN,垂足为F,且∠1=140°,则当
∠2=_______°时,AB∥CD.
50
【解析】当∠3=∠4时,AB∥CD.
∵∠1+∠3=180°,∠1=140°,
∴∠3=∠4=40°.
∵EF⊥MN,
∴∠2+∠4=90°,
∴∠2=50°.
3.如图所示,已知AF与BE相交于点O,点C,D分别是AF与BE上的两点,∠F=∠A,
∠A+∠ACD=180°,请说明CD∥EF的理由.
【解析】∵∠F=∠A,∠A+∠ACD=180°,
∴EF∥AB,AB∥CD,∴CD∥EF.
知识点2 平行判定的应用
4.(应用意识)(2024·汕头金平期中)已知直线BC,嘉嘉和琪琪想画出BC的平行线,他们
的方法如下:
下列说法正确的是 ( )
A.嘉嘉和琪琪的方法都正确
B.嘉嘉的方法不正确,琪琪的方法正确
C.嘉嘉的方法正确,琪琪的方法不正确
D.嘉嘉和琪琪的方法都不正确
A
【解析】嘉嘉的方法是通过同位角相等,两直线平行,得出BC∥DE;
琪琪的方法是通过内错角相等,两直线平行,得出BC∥DE.
5.如图所示,运动场上工作人员画了一条与各跑道分割线相交的直线,根据跑道分割
线与这条直线互相垂直,就能判定跑道分割线互相平行的理由是_______________
___________________________________.
在同一平面内,
垂直于同一直线的两条直线互相平行
6.(中华优秀传统文化)在后稷故里稷山县,有个流传三千多年的独特年俗,就是除夕
日农民在自家院子地面上绘“麦囤”图案,以期风调雨顺,四时平安,五谷丰登.如图1所
示的是“麦囤”示意图,乐乐为了验证“麦囤”图案中一组线段是否平行,测量了其中一
些角的度数,如图2所示,其中能说明a∥b的是 ( )
A.∠1=85°,∠4=85°
B.∠3=95°,∠4=85°
C.∠1=85°,∠3=95°
D.∠2=85°,∠4=85°
B
【解析】由∠1=85°,∠4=85°,不能判定a∥b,故A选项不符合题意;
∵∠3=95°,∠4=85°,∴∠3+∠4=180°,∴a∥b,故B选项符合题意;
由∠1=85°,∠3=95°,不能判定a∥b,故C选项不符合题意;
由∠2=85°,∠4=85°,不能判定a∥b,故D选项不符合题意.
7.如图所示的是一个可折叠的衣架,AB是地平线,当∠1=∠2时,PM∥AB,当∠3=∠4时,
PN∥AB,就可确定点N,P,M在同一条直线上,将下面正确的依据序号填写在横线上_______.
①两点确定一条直线;
②过直线外一点,有且只有一条直线与这条直线平行.
②
【解析】∵∠1=∠2,
∴PM∥AB,
∵∠3=∠4,∴PN∥AB,
∵过直线外一点,有且只有一条直线与这条直线平行,∴N,P,M在同一条直线上.
8.如图所示,已知∠1=40°,∠2=140°,∠3=40°,∠4=140°.试说明:a∥b,b∥c,d∥e,a∥c.
【解析】∵∠1=40°,∠2=140°,
∴∠1+∠2=180°,
∴a∥b,
∴∠5=∠1=40°;
∵∠3=40°,
∴∠5=∠3,∴d∥e;
∵∠4=140°,
且∠6+∠4=180°,
∴∠6=40°=∠3,
∴b∥c,∴a∥c.
9.(模型观念、推理能力)如图所示,在四边形ABCD中,∠A=∠C=90°.若BE,DF分别平
分∠MBC,∠NDC,问BE与DF的位置关系,并说明理由.
7.2.2 平行线的判定
课时目标 素养达成
1.经历探索两直线平行条件的过程,理解两直线平
行的条件,会运用条件判定两直线平行 推理能力、模型观念
2.掌握基本事实:两条直线被第三条直线所截,如果
同位角相等,那么这两条直线平行 几何直观、推理能力
3.探索并证明平行线的判定定理:两条直线被第三
条直线所截,如果内错角相等(或同旁内角互补),那
么这两条直线平行 推理能力、模型观念
4.进一步掌握直线平行的条件,并能解决一些简单
的问题.初步了解推理论证的方法,会正确书写简
单的推理过程 推理能力、模型观念
如图所示:两条直线AB,CD被第三条直线EF所截.
1.平行线的判定方法1
文字表述:同位角_________,两直线平行.
几何语言:∵∠1=________,∴AB_______CD.
2.平行线的判定方法2
文字表述:内错角_________,两直线平行.
几何语言:∵∠2=________,
∴AB_______CD.
相等
∠5
∥
相等
∠8
∥
3.平行线的判定方法3
文字表述:同旁内角_________,两直线平行.
几何语言:∵∠2+________=180°,
∴AB_______CD.
4.平行线的其他判定方法
(1)在同一平面内,平行于同一条直线的两条直线_________.
(2)在同一平面内,垂直于同一条直线的两条直线_________.
互补
∠5
∥
平行
平行
1.判断.(正确的画“√”,错误的画“×”)
(1)在同一平面内,a,b,c是直线,且a∥b,b∥c,则a∥c. ( )
(2)在同一平面内,a,b,c是直线,且a⊥b,b⊥c,则a⊥c. ( )
√
×
2.一个弯形管道ABCD的弯角∠ABC=130°,∠BCD=50°,则管道AB与CD的位置关系
是( )
A.平行 B.垂直
C.相交但不垂直 D.无法确定
A
3.如图所示,两块三角尺形状大小完全相同,边AB∥CD的依据是_____________
_____________.
同位角相等,
两直线平行
4.如图所示,一条街道的两个拐角∠ABC和∠BCD,若∠ABC=140°,要使街道AB和CD
在同一方向上,需要使∠BCD=________°,根据是_________________________.
140
内错角相等,两直线平行
【典例1】(教材再开发·P14练习T1变式)如图所示,∠1=∠3,∠1+∠2=180°,试说明
CD∥EF.
【自主解答】∵∠1=∠3,
∴AB∥EF.
∵∠4+∠2=180°,∠1+∠2=180°,
∴∠4=∠1,
∴CD∥AB,
∴CD∥EF.
平行线的判定(推理能力)
1.(2024·惠州惠城期末)如图所示,在①∠1=∠3,②∠2=∠3,③∠4=∠5,④∠2+∠4=180°中,
能判断直线l1∥l2的有 ( )
A.1个 B.2个
C.3个 D.4个
C
【解析】∵∠1=∠3,
∴l1∥l2(平行线的判定方法2).
∵∠4=∠5,
∴l1∥l2(平行线的判定方法1).
∵∠2+∠4=180°,
∴l1∥l2(平行线的判定方法3).
则能判断直线l1∥l2的有3个.
2.如图所示,(1)如果∠1=∠D,那么________∥________;
(2)如果∠1=∠B,那么________∥________;
(3)如果∠A+∠B=180°,那么________∥________;
(4)如果∠A+∠D=180°,那么________∥________.
AD
BC
AB
CD
AD
BC
AB
CD
【解析】(1)如果∠1=∠D,那么AD∥BC(内错角相等,两直线平行).
(2)如果∠1=∠B,那么AB∥CD(同位角相等,两直线平行).
(3)如果∠A+∠B=180°,那么AD∥BC(同旁内角互补,两直线平行).
(4)如果∠A+∠D=180°,那么AB∥CD(同旁内角互补,两直线平行).
【典例2】(教材再开发·P15练习T2变式)如图所示,王师傅将两块相同的长方形木板AB,CD平行放置并间隔一定距离,用长、宽相等的两块铁片a,b分别搭在AB,CD上,再用螺丝固定,做成了一个简易的冰箱底垫.已知∠1=90°,用量角器度量出哪一个角的度数,就可以判断铁片a与b是否平行
【自主解答】用量角器度量出∠3或∠2的度数,就可以判断铁片a与b是否为平行关系.
平行判定的应用(应用意识、推理能力)
1.(2024·韶关乳源期中)下列各图是由含30°角或45°角的直角三角尺组合而成的,其中
利用内错角相等画出AB∥CD的是 ( )
A.图1、图3 B.图2、图4
C.图1、图2、图4 D.图2、图3、图4
B
【解析】观察题图可得,图1由同位角相等,两直线平行,可以画出AB∥CD,故图1不符合题意;
图2∠BAD=∠ADC=30°,由内错角相等,两直线平行,可以画出AB∥CD,故图2符合题意;
图3∠B+∠D=90°+90°=180°,由同旁内角互补,两直线平行,可以画出AB∥CD,故图3不符合题意;
图4∠ABC=∠BCD=90°,由内错角相等,两直线平行,可以画出AB∥CD,故图4符合题意.
综上,利用内错角相等画出AB∥CD的是图2、图4.
2.如图表示钉在一起的木条a,b,c.若测得∠1=50°,∠2=75°,要使木条a∥b,木条a至少要
按图中所示方向旋转_______°.
25
【解析】如图所示,∵当∠2=∠1=50°时,AB∥b,∴要使木条a与b平行,木条a至少要按图中所示方向旋转75°-50°=25°.
1.(2024·佛山顺德期末)如图所示,直线a,b被直线c,d所截,则下列条件可以判定直线
c∥d的是 ( )
A.∠2=∠3
B.∠1=∠3
C.∠1+∠5=180°
D.∠4+∠5=180°
C
【解析】由∠2=∠3,不能判定c∥d,故A不符合题意;
∵∠1=∠3,
∴a∥b,故B不符合题意;
∵∠1+∠5=180°,
∴c∥d,故C符合题意;
∵∠4+∠5=180°,
∴a∥b,故D不符合题意.
2.平面内有两两不重合的直线l1,l2和l,已知l1⊥l,l2⊥l,则l1,l2的位置关系是 ( )
A.互相平行
B.可能平行,可能不平行
C.互相垂直
D.可能垂直,可能不垂直
A
【解析】∵l1⊥l,l2⊥l,∴∠1=∠2=90°,则l1∥l2.
3.如图所示,取一张长方形的硬纸片ABCD对折,MN是折痕,把面ABNM平摊在桌面上,
另一个面CDMN不论怎样改变位置,总有MN∥________∥________.因此________∥
________.
AB
CD
AB
CD
【解析】∵长方形的硬纸片ABCD对折,MN是折痕,
∴MN∥AB,MN∥CD,即MN∥AB∥CD,
∴AB∥CD(平行于同一直线的两条直线互相平行).
知识点1 平行线的判定
1.如图所示,过直线外一点画已知直线的平行线的方法叫“推平行线”法(图中三角形
ABC是三角尺),其依据是 ( )
A.同旁内角互补,两直线平行
B.两直线平行,同旁内角互补
C.同位角相等,两直线平行
D.两直线平行,同位角相等
【解析】∵∠1=∠2,∴a∥b(同位角相等,两直线平行),∴C正确.
C
2.(2024·清远清城期末)如图所示,已知直线EF⊥MN,垂足为F,且∠1=140°,则当
∠2=_______°时,AB∥CD.
50
【解析】当∠3=∠4时,AB∥CD.
∵∠1+∠3=180°,∠1=140°,
∴∠3=∠4=40°.
∵EF⊥MN,
∴∠2+∠4=90°,
∴∠2=50°.
3.如图所示,已知AF与BE相交于点O,点C,D分别是AF与BE上的两点,∠F=∠A,
∠A+∠ACD=180°,请说明CD∥EF的理由.
【解析】∵∠F=∠A,∠A+∠ACD=180°,
∴EF∥AB,AB∥CD,∴CD∥EF.
知识点2 平行判定的应用
4.(应用意识)(2024·汕头金平期中)已知直线BC,嘉嘉和琪琪想画出BC的平行线,他们
的方法如下:
下列说法正确的是 ( )
A.嘉嘉和琪琪的方法都正确
B.嘉嘉的方法不正确,琪琪的方法正确
C.嘉嘉的方法正确,琪琪的方法不正确
D.嘉嘉和琪琪的方法都不正确
A
【解析】嘉嘉的方法是通过同位角相等,两直线平行,得出BC∥DE;
琪琪的方法是通过内错角相等,两直线平行,得出BC∥DE.
5.如图所示,运动场上工作人员画了一条与各跑道分割线相交的直线,根据跑道分割
线与这条直线互相垂直,就能判定跑道分割线互相平行的理由是_______________
___________________________________.
在同一平面内,
垂直于同一直线的两条直线互相平行
6.(中华优秀传统文化)在后稷故里稷山县,有个流传三千多年的独特年俗,就是除夕
日农民在自家院子地面上绘“麦囤”图案,以期风调雨顺,四时平安,五谷丰登.如图1所
示的是“麦囤”示意图,乐乐为了验证“麦囤”图案中一组线段是否平行,测量了其中一
些角的度数,如图2所示,其中能说明a∥b的是 ( )
A.∠1=85°,∠4=85°
B.∠3=95°,∠4=85°
C.∠1=85°,∠3=95°
D.∠2=85°,∠4=85°
B
【解析】由∠1=85°,∠4=85°,不能判定a∥b,故A选项不符合题意;
∵∠3=95°,∠4=85°,∴∠3+∠4=180°,∴a∥b,故B选项符合题意;
由∠1=85°,∠3=95°,不能判定a∥b,故C选项不符合题意;
由∠2=85°,∠4=85°,不能判定a∥b,故D选项不符合题意.
7.如图所示的是一个可折叠的衣架,AB是地平线,当∠1=∠2时,PM∥AB,当∠3=∠4时,
PN∥AB,就可确定点N,P,M在同一条直线上,将下面正确的依据序号填写在横线上_______.
①两点确定一条直线;
②过直线外一点,有且只有一条直线与这条直线平行.
②
【解析】∵∠1=∠2,
∴PM∥AB,
∵∠3=∠4,∴PN∥AB,
∵过直线外一点,有且只有一条直线与这条直线平行,∴N,P,M在同一条直线上.
8.如图所示,已知∠1=40°,∠2=140°,∠3=40°,∠4=140°.试说明:a∥b,b∥c,d∥e,a∥c.
【解析】∵∠1=40°,∠2=140°,
∴∠1+∠2=180°,
∴a∥b,
∴∠5=∠1=40°;
∵∠3=40°,
∴∠5=∠3,∴d∥e;
∵∠4=140°,
且∠6+∠4=180°,
∴∠6=40°=∠3,
∴b∥c,∴a∥c.
9.(模型观念、推理能力)如图所示,在四边形ABCD中,∠A=∠C=90°.若BE,DF分别平
分∠MBC,∠NDC,问BE与DF的位置关系,并说明理由.
同课章节目录
