7.2.3 平行线的性质 课件(共46张PPT)
文档属性
| 名称 | 7.2.3 平行线的性质 课件(共46张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 21:18:40 | ||
图片预览







文档简介
(共46张PPT)
7.2.3 平行线的性质
课时目标 素养达成
1.掌握平行线的性质定理:两条平行线被第三
条直线所截,同位角相等 几何直观、推理能力、模型观念
2.探索并证明平行线的性质定理:两条平行线
被第三条直线所截,内错角相等(或同旁内角互
补) 几何直观、推理能力、模型观念
3.能用平行线的性质进行简单的推理和计算 推理能力、模型观念
4.能熟练地运用平行线的判定与性质进行推
理和计算 推理能力、模型观念、运算能力
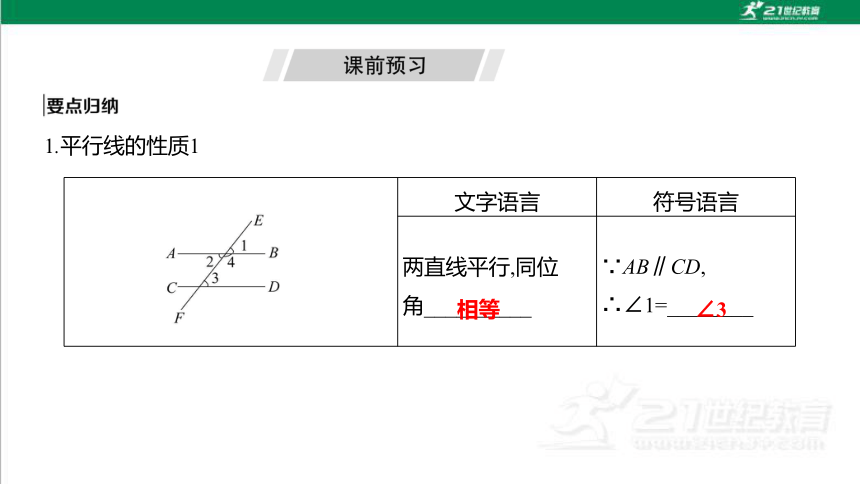
1.平行线的性质1
文字语言 符号语言
两直线平行,同位
角__________ ∵AB∥CD,
∴∠1=________
相等
∠3
2.平行线的性质2
文字语言 符号语言
两直线平行,内错角__________ ∵AB∥CD,
∴∠2=________
相等
∠3
3.平行线的性质3
文字语言 符号语言
两直线平行,同旁内角
__________ ∵AB∥CD,
∴∠3+∠4=180°
互补
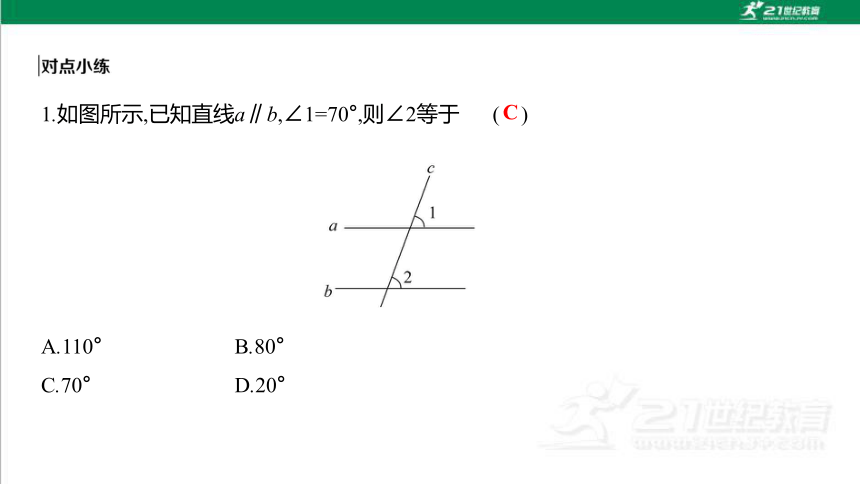
1.如图所示,已知直线a∥b,∠1=70°,则∠2等于 ( )
A.110° B.80°
C.70° D.20°
C
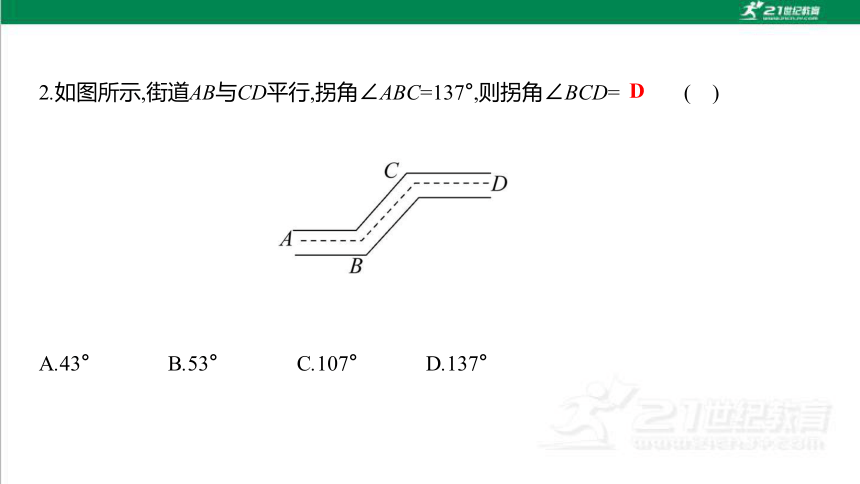
2.如图所示,街道AB与CD平行,拐角∠ABC=137°,则拐角∠BCD= ( )
A.43° B.53° C.107° D.137°
D
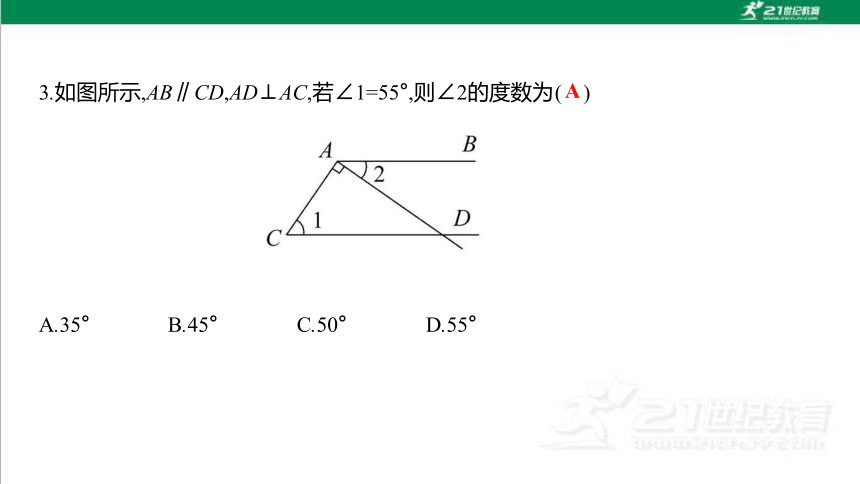
3.如图所示,AB∥CD,AD⊥AC,若∠1=55°,则∠2的度数为 ( )
A.35° B.45° C.50° D.55°
A
平行线的性质(推理能力)
1.(2024·包头中考)如图所示,直线AB∥CD,点E在直线AB上,射线EF交直线CD于点G,
则图中与∠AEF互补的角有 ( )
A.1个 B.2个 C.3个 D.4个
C
【解析】∵∠AEF+∠FEB=180°,
∴∠AEF与∠FEB互补.
∵AB∥CD,
∴∠FGD=∠FEB,∠CGE=∠FEB,
∴∠AEF与∠FGD,∠CGE互补.
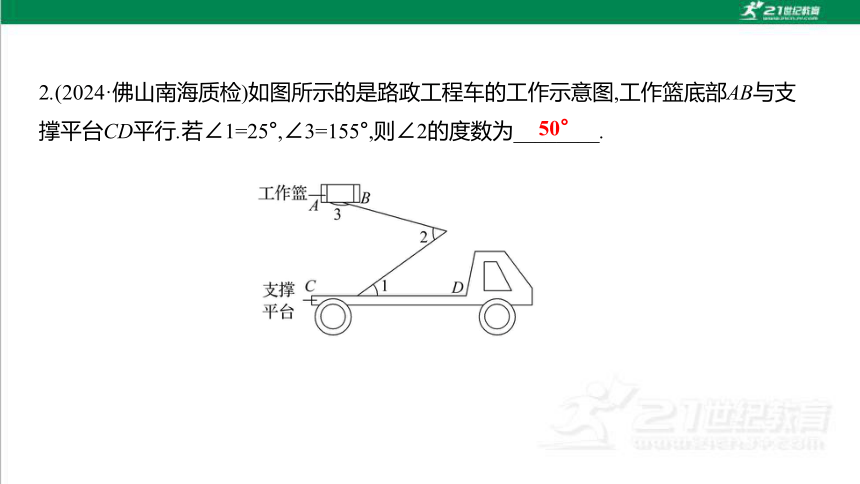
2.(2024·佛山南海质检)如图所示的是路政工程车的工作示意图,工作篮底部AB与支
撑平台CD平行.若∠1=25°,∠3=155°,则∠2的度数为________.
50°
【解析】如图所示,过∠NOM的顶点O作直线EF∥CD,
∵AB∥CD,
∴AB∥EF∥CD,
∴∠1=∠EOM=25°,∠EON+∠3=180°,
∴∠EON=180°-155°=25°,
∴∠MON=25°+25°=50°.
【典例2】(教材再开发·P18例4拓展)如图所示,已知∠D=108°,∠BAD=72°,AC⊥BC于点C,EF⊥BC于点F.
试说明:∠1=∠2.
平行线的性质与判定的综合应用(推理能力)
【自主解答】∵∠D=108°,∠BAD=72°(已知),∴∠D+∠BAD=180°,
∴AB∥CD(同旁内角互补,两直线平行),
∴∠1=∠3(两直线平行,内错角相等).
又∵AC⊥BC于点C,EF⊥BC于点F(已知),∴∠ACB=∠EFB=90°,
∴EF∥AC(同位角相等,两直线平行),
∴∠2=∠3(两直线平行,同位角相等),
∴∠1=∠2(等量代换).
1.(2024·兰州模拟)如图所示,已知∠1=∠2,∠3=118°,则∠4= ( )
A.48° B.62°
C.68° D.72°
B
【解析】如图所示,
∵∠1=∠2,∴a∥b,
∴∠4=∠5,
∵∠3=118°,∠3+∠5=180°,∴∠5=62°,
∴∠4=62°.
2.填空完成下面说理过程.
已知:如图所示,∠1=∠2,BE,DF分别是∠ABC与∠ADE的平分线.试说明DE∥BC.
解:∵∠1=∠2(_________),
∴DF∥BE(_________________________),
∴∠3=∠______(_________________________).
∵BE,DF分别是∠ABC与∠ADE的平分线(_________),
∴∠ADE=2∠4,∠ABC=2∠______(___________________),
∴∠ADE=∠ABC,
∴DE∥BC(_________________________).
已知
内错角相等,两直线平行
4
两直线平行,同位角相等
已知
3
角平分线的定义
同位角相等,两直线平行
【解析】∵∠1=∠2(已知),
∴DF∥BE(内错角相等,两直线平行),
∴∠3=∠4(两直线平行,同位角相等).
∵BE,DF分别是∠ABC与∠ADE的平分线(已知),
∴∠ADE=2∠4,∠ABC=2∠3(角平分线的定义),
∴∠ADE=∠ABC,
∴DE∥BC(同位角相等,两直线平行).
1.如图所示,已知直线a⊥c,b⊥c,如果∠1=70°,那么∠2的度数是 ( )
A.70° B.100° C.110° D.120°
C
【解析】∵直线a⊥c,b⊥c,∴a∥b,
∴∠2=∠3,∵∠1=70°,
∴∠3=180°-∠1=110°,
∴∠2=110°.
2.如图所示,AB⊥AE,AB∥CD,∠CAE=42°,则∠ACD=_________.
132°
【解析】∵AB⊥AE,∠CAE=42°,∴∠BAC=90°-42°=48°,
∵AB∥CD,∴∠BAC+∠ACD=180°,
∴∠ACD=132°.
3.如图所示,DE∥AB,BF交DE于点C,∠ABC=∠ADC.
(1)AD与BF平行吗 请说明理由.
(2)若BD平分∠ABC,且∠1+∠2=115°,求∠2的度数.
【解析】(1)AD∥BF,理由如下:
∵DE∥AB,
∴∠ABC=∠BCE,
∵∠ABC=∠ADC,
∴∠BCE=∠ADC,
∴AD∥BF.
知识点1 平行线的性质
1.(中华优秀传统文化)杆秤是中国古老的称量工具,在我国已经使用了数千年.如图
所示,是杆秤在称物时的状态,其中秤纽AB和拴秤砣的细线CD都是铅垂线.若∠1=102°,
则∠2的度数为 ( )
A.78° B.102° C.68° D.88°
A
【解析】∵∠1=102°,
∴∠BCD=180°-102°=78°,∵AB∥CD,
∴∠2=∠BCD=78°.
2.(2024·广州花都期中)如图所示,把长方形ABCD沿EF折叠后,点D,C分别落在D',C'的
位置,若∠1=50°,则∠FGD'=________°.
130
【解析】∵AD∥BC,∠1=50°,
∴∠BGE=∠DEG=180°-∠1=130°,
∴∠FGD'=∠BGE=130°.
3.如图所示,AB∥CD,∠1=∠B.试说明:CD是∠BCE的平分线.
解:∵AB∥CD(已知),
∴∠2=________(_________________________).
又∵∠1=∠B(已知),
∴________=________(_____________),
即CD是∠BCE的平分线.
∠B
两直线平行,内错角相等
∠1
∠2
等量代换
【解析】∵AB∥CD(已知),
∴∠2=∠B(两直线平行,内错角相等),
又∵∠1=∠B(已知),
∴∠1=∠2(等量代换),
即CD是∠BCE的平分线.
知识点2 平行线性质和判定的综合应用
4.(2024·茂名化州期末)如图所示,已知a⊥c,b⊥c,若∠1=65°,则∠2等于 ( )
A.65° B.90°
C.25° D.70°
A
【解析】因为a⊥c,b⊥c,
所以a∥b,
所以∠1=∠3=65°,
所以∠2=∠3=65°.
5.如图所示,AC∥DF,直线AF分别与直线BD,CE相交于点G,H,∠1=∠2.
(1)试说明BD∥CE;
(2)试说明∠C=∠D.
【解析】(1)∵∠1=∠2,∠1=∠DGF,
∴∠2=∠DGF,∴BD∥CE.
(2)∵DB∥CE,
∴∠C=∠DBA.
又∵AC∥DF,
∴∠D=∠DBA,
∴∠C=∠D.
6.(跨学科·物理)光在不同介质中的传播速度是不同的,因此当光线从水中射向空气
时要发生折射.如图所示,∠1=70°,∠2=175°,则∠3的度数是 ( )
A.70° B.80° C.85° D.75°
D
【解析】如图所示,
∵AB∥CD,∠1=70°,
∴∠MND=∠1=70°,
∵∠MND+∠END=∠2=175°,
∴∠END=105°,
∵CD∥EF,∴∠END+∠3=180°,
∴∠3=75°.
7.(2024·梅州五华期中)如图所示,AB⊥PQ,CD⊥PQ,垂足分别为B和D,BF和DE分别平
分∠ABP和∠CDP.在①AB∥CD;②∠1=∠2;③CD⊥EF;④∠E+∠F=180°中,结论正确
的序号是 ( )
A.①②③ B.②③④
C.①②④ D.③④
C
8.如图所示,AB∥CD,N是CD上一点,M是AB,CD外一点,连接BM,NM,若∠CNM=70°,∠ABM=110°,则∠M的度数为_______°.
40
【解析】如图所示,过点M作ME∥AB,
∴∠ABM+∠EMB=180°,∵∠ABM=110°,
∴∠EMB=70°,∵AB∥CD,
∴ME∥CD,∴∠CNM+∠EMN=180°,
∵∠CNM=70°,
∴∠EMN=110°,
∴∠BMN=∠EMN-∠EMB=40°.
9.一副三角尺和一张对边平行的纸条按如图所示方式摆放,求∠1的度数.
【解析】延长AB交直线CD于点M,
∵AM⊥CE,DF⊥CE,
∴AM∥DF,
∴∠AMC=∠FDM=60°,
∵AG∥CD,
∴∠AMC=∠GAM=60°,
∵∠BAE=45°,
∴∠1=∠GAM-∠EAB=60°-45°=15°.
10.(应用意识、推理能力)(2024·浏阳期中)探索发现:(1)如图1所示,已知直线AC∥BD.若∠ACP=30°,∠BDP=45°,求∠CPD的度数;
归纳总结:(2)根据(1)中的问题,直接写出图中∠ACP,∠BDP,∠CPD之间的数量关系________________;
实践应用:(3)如图2所示,水务公司在由西向东铺设供水管道,他们从点A铺设到点B时发现了一个障碍物,不得不改变方向绕开障碍物,计划改为沿南偏东30°方向埋设到点C,再沿障碍物边缘埋设到点D处,测得∠BCD=65°.若要恢复原来的正东方向DE,则∠CDE应等于多少度
【解析】(1)过点P作PQ∥AC,如图1所示.
∵PQ∥AC,AC∥BD,∴AC∥PQ∥BD,
∴∠CPQ=∠ACP,∠DPQ=∠BDP,
∴∠CPQ+∠DPQ=∠ACP+∠BDP,即∠CPD=∠ACP+∠BDP.
∵∠ACP=30°,∠BDP=45°,∴∠CPD=∠ACP+∠BDP=75°.
(2)由(1),得∠ACP,∠BDP,∠CPD之间的数量关系为∠CPD=∠ACP+∠BDP.
(3)如图2所示,过点D作DF⊥DE,
则BM∥DF,∠EDF=90°,
由(2),得∠BCD=∠CBM+∠CDF,
∵∠BCD=65°,
∠CBM=30°,
∴∠CDF=35°,
∴∠CDE=∠CDF+∠EDF=125°.
7.2.3 平行线的性质
课时目标 素养达成
1.掌握平行线的性质定理:两条平行线被第三
条直线所截,同位角相等 几何直观、推理能力、模型观念
2.探索并证明平行线的性质定理:两条平行线
被第三条直线所截,内错角相等(或同旁内角互
补) 几何直观、推理能力、模型观念
3.能用平行线的性质进行简单的推理和计算 推理能力、模型观念
4.能熟练地运用平行线的判定与性质进行推
理和计算 推理能力、模型观念、运算能力
1.平行线的性质1
文字语言 符号语言
两直线平行,同位
角__________ ∵AB∥CD,
∴∠1=________
相等
∠3
2.平行线的性质2
文字语言 符号语言
两直线平行,内错角__________ ∵AB∥CD,
∴∠2=________
相等
∠3
3.平行线的性质3
文字语言 符号语言
两直线平行,同旁内角
__________ ∵AB∥CD,
∴∠3+∠4=180°
互补
1.如图所示,已知直线a∥b,∠1=70°,则∠2等于 ( )
A.110° B.80°
C.70° D.20°
C
2.如图所示,街道AB与CD平行,拐角∠ABC=137°,则拐角∠BCD= ( )
A.43° B.53° C.107° D.137°
D
3.如图所示,AB∥CD,AD⊥AC,若∠1=55°,则∠2的度数为 ( )
A.35° B.45° C.50° D.55°
A
平行线的性质(推理能力)
1.(2024·包头中考)如图所示,直线AB∥CD,点E在直线AB上,射线EF交直线CD于点G,
则图中与∠AEF互补的角有 ( )
A.1个 B.2个 C.3个 D.4个
C
【解析】∵∠AEF+∠FEB=180°,
∴∠AEF与∠FEB互补.
∵AB∥CD,
∴∠FGD=∠FEB,∠CGE=∠FEB,
∴∠AEF与∠FGD,∠CGE互补.
2.(2024·佛山南海质检)如图所示的是路政工程车的工作示意图,工作篮底部AB与支
撑平台CD平行.若∠1=25°,∠3=155°,则∠2的度数为________.
50°
【解析】如图所示,过∠NOM的顶点O作直线EF∥CD,
∵AB∥CD,
∴AB∥EF∥CD,
∴∠1=∠EOM=25°,∠EON+∠3=180°,
∴∠EON=180°-155°=25°,
∴∠MON=25°+25°=50°.
【典例2】(教材再开发·P18例4拓展)如图所示,已知∠D=108°,∠BAD=72°,AC⊥BC于点C,EF⊥BC于点F.
试说明:∠1=∠2.
平行线的性质与判定的综合应用(推理能力)
【自主解答】∵∠D=108°,∠BAD=72°(已知),∴∠D+∠BAD=180°,
∴AB∥CD(同旁内角互补,两直线平行),
∴∠1=∠3(两直线平行,内错角相等).
又∵AC⊥BC于点C,EF⊥BC于点F(已知),∴∠ACB=∠EFB=90°,
∴EF∥AC(同位角相等,两直线平行),
∴∠2=∠3(两直线平行,同位角相等),
∴∠1=∠2(等量代换).
1.(2024·兰州模拟)如图所示,已知∠1=∠2,∠3=118°,则∠4= ( )
A.48° B.62°
C.68° D.72°
B
【解析】如图所示,
∵∠1=∠2,∴a∥b,
∴∠4=∠5,
∵∠3=118°,∠3+∠5=180°,∴∠5=62°,
∴∠4=62°.
2.填空完成下面说理过程.
已知:如图所示,∠1=∠2,BE,DF分别是∠ABC与∠ADE的平分线.试说明DE∥BC.
解:∵∠1=∠2(_________),
∴DF∥BE(_________________________),
∴∠3=∠______(_________________________).
∵BE,DF分别是∠ABC与∠ADE的平分线(_________),
∴∠ADE=2∠4,∠ABC=2∠______(___________________),
∴∠ADE=∠ABC,
∴DE∥BC(_________________________).
已知
内错角相等,两直线平行
4
两直线平行,同位角相等
已知
3
角平分线的定义
同位角相等,两直线平行
【解析】∵∠1=∠2(已知),
∴DF∥BE(内错角相等,两直线平行),
∴∠3=∠4(两直线平行,同位角相等).
∵BE,DF分别是∠ABC与∠ADE的平分线(已知),
∴∠ADE=2∠4,∠ABC=2∠3(角平分线的定义),
∴∠ADE=∠ABC,
∴DE∥BC(同位角相等,两直线平行).
1.如图所示,已知直线a⊥c,b⊥c,如果∠1=70°,那么∠2的度数是 ( )
A.70° B.100° C.110° D.120°
C
【解析】∵直线a⊥c,b⊥c,∴a∥b,
∴∠2=∠3,∵∠1=70°,
∴∠3=180°-∠1=110°,
∴∠2=110°.
2.如图所示,AB⊥AE,AB∥CD,∠CAE=42°,则∠ACD=_________.
132°
【解析】∵AB⊥AE,∠CAE=42°,∴∠BAC=90°-42°=48°,
∵AB∥CD,∴∠BAC+∠ACD=180°,
∴∠ACD=132°.
3.如图所示,DE∥AB,BF交DE于点C,∠ABC=∠ADC.
(1)AD与BF平行吗 请说明理由.
(2)若BD平分∠ABC,且∠1+∠2=115°,求∠2的度数.
【解析】(1)AD∥BF,理由如下:
∵DE∥AB,
∴∠ABC=∠BCE,
∵∠ABC=∠ADC,
∴∠BCE=∠ADC,
∴AD∥BF.
知识点1 平行线的性质
1.(中华优秀传统文化)杆秤是中国古老的称量工具,在我国已经使用了数千年.如图
所示,是杆秤在称物时的状态,其中秤纽AB和拴秤砣的细线CD都是铅垂线.若∠1=102°,
则∠2的度数为 ( )
A.78° B.102° C.68° D.88°
A
【解析】∵∠1=102°,
∴∠BCD=180°-102°=78°,∵AB∥CD,
∴∠2=∠BCD=78°.
2.(2024·广州花都期中)如图所示,把长方形ABCD沿EF折叠后,点D,C分别落在D',C'的
位置,若∠1=50°,则∠FGD'=________°.
130
【解析】∵AD∥BC,∠1=50°,
∴∠BGE=∠DEG=180°-∠1=130°,
∴∠FGD'=∠BGE=130°.
3.如图所示,AB∥CD,∠1=∠B.试说明:CD是∠BCE的平分线.
解:∵AB∥CD(已知),
∴∠2=________(_________________________).
又∵∠1=∠B(已知),
∴________=________(_____________),
即CD是∠BCE的平分线.
∠B
两直线平行,内错角相等
∠1
∠2
等量代换
【解析】∵AB∥CD(已知),
∴∠2=∠B(两直线平行,内错角相等),
又∵∠1=∠B(已知),
∴∠1=∠2(等量代换),
即CD是∠BCE的平分线.
知识点2 平行线性质和判定的综合应用
4.(2024·茂名化州期末)如图所示,已知a⊥c,b⊥c,若∠1=65°,则∠2等于 ( )
A.65° B.90°
C.25° D.70°
A
【解析】因为a⊥c,b⊥c,
所以a∥b,
所以∠1=∠3=65°,
所以∠2=∠3=65°.
5.如图所示,AC∥DF,直线AF分别与直线BD,CE相交于点G,H,∠1=∠2.
(1)试说明BD∥CE;
(2)试说明∠C=∠D.
【解析】(1)∵∠1=∠2,∠1=∠DGF,
∴∠2=∠DGF,∴BD∥CE.
(2)∵DB∥CE,
∴∠C=∠DBA.
又∵AC∥DF,
∴∠D=∠DBA,
∴∠C=∠D.
6.(跨学科·物理)光在不同介质中的传播速度是不同的,因此当光线从水中射向空气
时要发生折射.如图所示,∠1=70°,∠2=175°,则∠3的度数是 ( )
A.70° B.80° C.85° D.75°
D
【解析】如图所示,
∵AB∥CD,∠1=70°,
∴∠MND=∠1=70°,
∵∠MND+∠END=∠2=175°,
∴∠END=105°,
∵CD∥EF,∴∠END+∠3=180°,
∴∠3=75°.
7.(2024·梅州五华期中)如图所示,AB⊥PQ,CD⊥PQ,垂足分别为B和D,BF和DE分别平
分∠ABP和∠CDP.在①AB∥CD;②∠1=∠2;③CD⊥EF;④∠E+∠F=180°中,结论正确
的序号是 ( )
A.①②③ B.②③④
C.①②④ D.③④
C
8.如图所示,AB∥CD,N是CD上一点,M是AB,CD外一点,连接BM,NM,若∠CNM=70°,∠ABM=110°,则∠M的度数为_______°.
40
【解析】如图所示,过点M作ME∥AB,
∴∠ABM+∠EMB=180°,∵∠ABM=110°,
∴∠EMB=70°,∵AB∥CD,
∴ME∥CD,∴∠CNM+∠EMN=180°,
∵∠CNM=70°,
∴∠EMN=110°,
∴∠BMN=∠EMN-∠EMB=40°.
9.一副三角尺和一张对边平行的纸条按如图所示方式摆放,求∠1的度数.
【解析】延长AB交直线CD于点M,
∵AM⊥CE,DF⊥CE,
∴AM∥DF,
∴∠AMC=∠FDM=60°,
∵AG∥CD,
∴∠AMC=∠GAM=60°,
∵∠BAE=45°,
∴∠1=∠GAM-∠EAB=60°-45°=15°.
10.(应用意识、推理能力)(2024·浏阳期中)探索发现:(1)如图1所示,已知直线AC∥BD.若∠ACP=30°,∠BDP=45°,求∠CPD的度数;
归纳总结:(2)根据(1)中的问题,直接写出图中∠ACP,∠BDP,∠CPD之间的数量关系________________;
实践应用:(3)如图2所示,水务公司在由西向东铺设供水管道,他们从点A铺设到点B时发现了一个障碍物,不得不改变方向绕开障碍物,计划改为沿南偏东30°方向埋设到点C,再沿障碍物边缘埋设到点D处,测得∠BCD=65°.若要恢复原来的正东方向DE,则∠CDE应等于多少度
【解析】(1)过点P作PQ∥AC,如图1所示.
∵PQ∥AC,AC∥BD,∴AC∥PQ∥BD,
∴∠CPQ=∠ACP,∠DPQ=∠BDP,
∴∠CPQ+∠DPQ=∠ACP+∠BDP,即∠CPD=∠ACP+∠BDP.
∵∠ACP=30°,∠BDP=45°,∴∠CPD=∠ACP+∠BDP=75°.
(2)由(1),得∠ACP,∠BDP,∠CPD之间的数量关系为∠CPD=∠ACP+∠BDP.
(3)如图2所示,过点D作DF⊥DE,
则BM∥DF,∠EDF=90°,
由(2),得∠BCD=∠CBM+∠CDF,
∵∠BCD=65°,
∠CBM=30°,
∴∠CDF=35°,
∴∠CDE=∠CDF+∠EDF=125°.
同课章节目录
