12.2.2 直方图 课件(共28张PPT)
文档属性
| 名称 | 12.2.2 直方图 课件(共28张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 21:29:02 | ||
图片预览







文档简介
(共28张PPT)
12.2.2 直方图
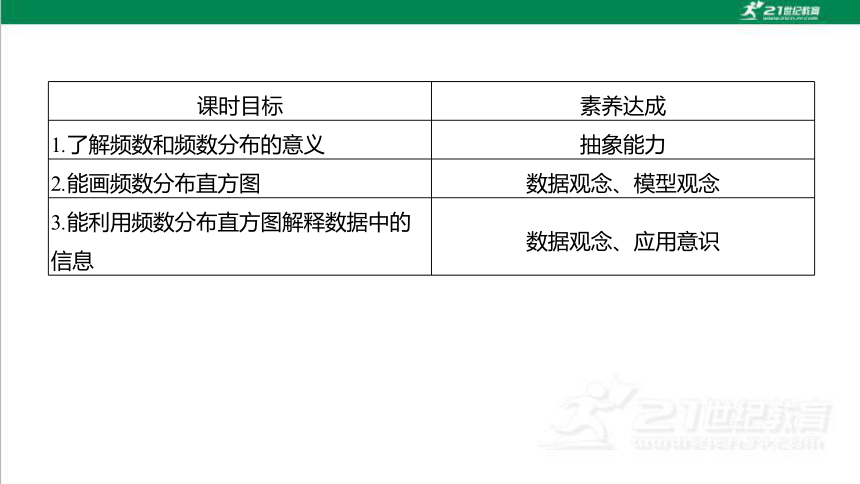
课时目标 素养达成
1.了解频数和频数分布的意义 抽象能力
2.能画频数分布直方图 数据观念、模型观念
3.能利用频数分布直方图解释数据中的信息 数据观念、应用意识
端点
距离
组数
没有
越多
5~12
(2)频数:落在各个小组内的数据的_________.
(3)频数分布直方图中的频数:以小长方形的_________来反映,等距分组时,一般直接用小长方形的_______表示频数.
2.频数分布直方图的制作与阅读
(1)画频数分布直方图的步骤
①计算___________与___________的差.
②决定_________和_________.
③列_____________表.
④画频数分布直方图.
(2)结合频数分布表去理解频数分布直方图中的信息.
个数
面积
高
最大值
最小值
组距
组数
频数分布
1.将数据83,85,87,89,84,85,86,88,87分组,86.5~88.5这一组的频数是( )
A.2 B.3 C.4 D.0.3
2.有一组数据,最小55,最大98,若组距为6,则这组数据可分成( )
A.7组 B.8组 C.9组 D.10组
3.一组数据共有50个数,最大的数为100,最小的数为70.如果准备将这组数据分为5组,
那么组距应是( )
A.5 B.6 C.7 D.8
B
B
B
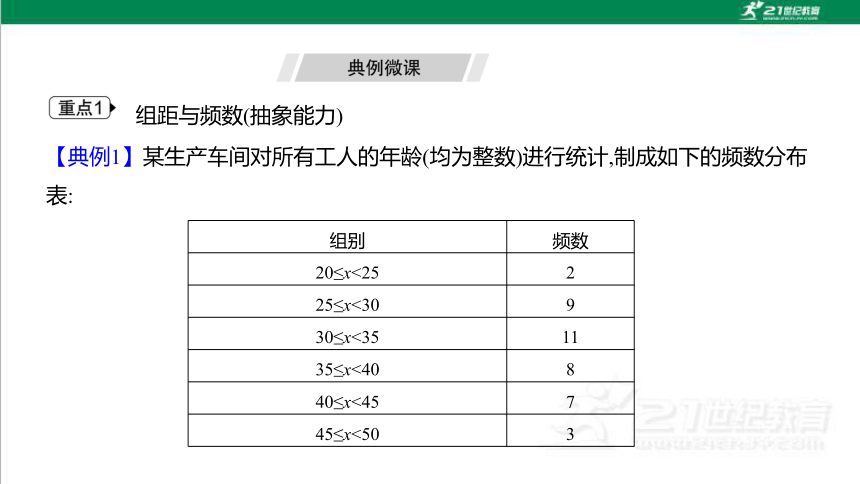
【典例1】某生产车间对所有工人的年龄(均为整数)进行统计,制成如下的频数分布表:
组距与频数(抽象能力)
组别 频数
20≤x<25 2
25≤x<30 9
30≤x<35 11
35≤x<40 8
40≤x<45 7
45≤x<50 3
1.在一次调查中,出现A种情况的频率为0.3,其余情况出现的频数之和为70,则调查的总数为( )
A.140 B.100 C.90 D.70
【解析】70÷(1-0.3)=100.
2.统计得到一组数据,其中最大值是136,最小值是52,取组距为10,可以分成( )
A.10组 B.9组 C.8组 D.7组
【解析】在样本数据中最大值为136,最小值为52,它们的差是136-52=84,已知组距为10,由于84÷10=8.4,故可以分成9组.
B
B
【典例2】(教材再开发·P168例3拓展)梁启超的《少年中国说》:“少年强则国强”,加强体育锻炼,增强学生体质是学校的重要工作.某校为了解七年级男生的“一分钟跳绳”项目的训练情况,从全校七年级男生中随机抽取50名男生为样本进行了测试.根据测试结果,绘制出部分频数分布表和部分频数分布直方图如下所示:
频数分布表与直方图(数据观念、模型意识)
组别 次数x 频数(人数)
第1组 80≤x<100 6
第2组 100≤x<120 8
第3组 120≤x<140 a
第4组 140≤x<160 18
第5组 160≤x<180 6
请结合图表完成下列问题:
(1)填空:表中a=________,并补全频数分布直方图.
(2)如果将其绘制成扇形统计图,请求出第5组所在扇形圆心角的度数.
(3)这50名男生中,一分钟跳绳次数不低于140的人数占抽取学生总人数的百分之几
(4)如果这个学校七年级男生一共500人,请你估计一分钟跳绳次数在160≤x<180的有多少人.
(2024·汕头潮南质检)某次数学测试,抽取部分同学的成绩(得分为整数),整理制成如
图所示的频数分布直方图,根据图示信息描述不正确的是( )
A.频数分布直方图中组距是10
B.本次抽样样本容量是60
C.70.5~80.5这一分数段的频数为18
D.估计这次数学测试及格(不低于60
分)率为92%
B
1.(2024·云浮新兴期中)统计得到一组数据最大值为145,最小值为30,取组距为20,可
分成( )
A.3组 B.4组 C.5组 D.6组
【解析】在样本数据中最大值为145,最小值为30,它们的差是145-30=115,
已知组距为20,由于115÷20≈6,故可以分成6组.
D
2.(2024·汕头潮南质检)某学校随机抽取了400名学生的测试成绩作为样本,数据整理
如表所示,则等级为A和B的共有________人.
等级 A B C D
频数 150 4
频率 0.18
324
3.为了普及足球运动的有关知识,某校举办了一场关于足球运动的知识竞赛.为了解此次知识竞赛成绩的情况,随机抽取了部分参赛学生的成绩,得到频数分布直方图,如图(每组含前一个边界值,不含后一个边界值).请根据该直方图,回答下列问题:
(1)数据分组时的组距为________分.
(2)自左至右分别为第1,2,3,4组,频数最大的是哪一组
(3)学校决定为成绩在80分以上(包括80分)的学生颁发优秀证书,若该校共有800名学生,请估计能拿到优秀证书的学生人数.
C
12
知识点2 频数分布表与直方图
3.某班将安全知识竞赛成绩整理后绘制成频数分布直方图,图中从左至右前四组的
百分比分别是4%,12%,40%,28%,第五组的频数是8,下列结论中错误的是( )
A.80分以上的学生有14名
B.该班有50名同学参赛
C.成绩在70~80分的人数最多
D.第五组的百分比为16%
A
【解析】该班参赛的学生有8÷(1-4%-12%-40%-28%)=50(名),故选项B说法正确;
80分以上的学生有50×28%+8=22(名),故选项A说法错误;成绩在70~80分的人数最多,故选项C说法正确;
第五组的百分比为8÷50×100%=16%,故选项D说法正确.
B
5.(易错警示题·隐含条件未挖掘)某中学七年级甲、乙、丙三个班中,每班的学生人数都为40,某次数学考试的成绩统计如图表所示(每组分数含最小值,不含最大值).根据图表提供的信息﹐则80≤x<90分这一组人数最多的班是_________.
丙班数学成绩频数统计表
分数 50≤x
<60 60≤x
<70 70≤x
<80 80≤x
<90 90≤x
<100
人数 1 4 15 11 9
甲班
【解析】由甲班数学成绩频数分布直方图可知,80≤x<90分这一组人数大于12,由乙班数学成绩各分数段人数统计图可知,80≤x<90分这一组人数是40×(1-10%-5%-35%-20%)=12,由丙班数学成绩频数统计表可知,80≤x<90分这一组人数是11,所以甲班在80≤x<90分这一组人数最多.
6.(应用意识)
如图为国家节水标志,节水标志各部分的含义为:圆形代表地球,标志留白部分像一只手托起一滴水,手又像一条蜿蜒的河流,象征滴水汇成江河.某市在实施居民用水定额管理前,对居民生活用水情况进行了调查,通过简单随机抽样调查获得了50个家庭去年的月均用水量(单位:吨).以下是整理数据后的不完整图表.
月均用水量频数分布表
分组 频数
2≤x<3 4
3≤x<4 12
4≤x<5 a
5≤x<6 9
6≤x<7 5
7≤x<8 4
8≤x<9 2
合计 50
请根据图表中提供的信息解答下列问题:
(1)表中a的值为________,请补全频数分布直方图;
(2)在扇形图中,月均用水量为“E:6≤x<7”的扇形的圆心角是________°;
(3)为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费.若要使60%的家庭水费支出不受影响,你觉得家庭月均用水量应该定为多少 为什么
12.2.2 直方图
课时目标 素养达成
1.了解频数和频数分布的意义 抽象能力
2.能画频数分布直方图 数据观念、模型观念
3.能利用频数分布直方图解释数据中的信息 数据观念、应用意识
端点
距离
组数
没有
越多
5~12
(2)频数:落在各个小组内的数据的_________.
(3)频数分布直方图中的频数:以小长方形的_________来反映,等距分组时,一般直接用小长方形的_______表示频数.
2.频数分布直方图的制作与阅读
(1)画频数分布直方图的步骤
①计算___________与___________的差.
②决定_________和_________.
③列_____________表.
④画频数分布直方图.
(2)结合频数分布表去理解频数分布直方图中的信息.
个数
面积
高
最大值
最小值
组距
组数
频数分布
1.将数据83,85,87,89,84,85,86,88,87分组,86.5~88.5这一组的频数是( )
A.2 B.3 C.4 D.0.3
2.有一组数据,最小55,最大98,若组距为6,则这组数据可分成( )
A.7组 B.8组 C.9组 D.10组
3.一组数据共有50个数,最大的数为100,最小的数为70.如果准备将这组数据分为5组,
那么组距应是( )
A.5 B.6 C.7 D.8
B
B
B
【典例1】某生产车间对所有工人的年龄(均为整数)进行统计,制成如下的频数分布表:
组距与频数(抽象能力)
组别 频数
20≤x<25 2
25≤x<30 9
30≤x<35 11
35≤x<40 8
40≤x<45 7
45≤x<50 3
1.在一次调查中,出现A种情况的频率为0.3,其余情况出现的频数之和为70,则调查的总数为( )
A.140 B.100 C.90 D.70
【解析】70÷(1-0.3)=100.
2.统计得到一组数据,其中最大值是136,最小值是52,取组距为10,可以分成( )
A.10组 B.9组 C.8组 D.7组
【解析】在样本数据中最大值为136,最小值为52,它们的差是136-52=84,已知组距为10,由于84÷10=8.4,故可以分成9组.
B
B
【典例2】(教材再开发·P168例3拓展)梁启超的《少年中国说》:“少年强则国强”,加强体育锻炼,增强学生体质是学校的重要工作.某校为了解七年级男生的“一分钟跳绳”项目的训练情况,从全校七年级男生中随机抽取50名男生为样本进行了测试.根据测试结果,绘制出部分频数分布表和部分频数分布直方图如下所示:
频数分布表与直方图(数据观念、模型意识)
组别 次数x 频数(人数)
第1组 80≤x<100 6
第2组 100≤x<120 8
第3组 120≤x<140 a
第4组 140≤x<160 18
第5组 160≤x<180 6
请结合图表完成下列问题:
(1)填空:表中a=________,并补全频数分布直方图.
(2)如果将其绘制成扇形统计图,请求出第5组所在扇形圆心角的度数.
(3)这50名男生中,一分钟跳绳次数不低于140的人数占抽取学生总人数的百分之几
(4)如果这个学校七年级男生一共500人,请你估计一分钟跳绳次数在160≤x<180的有多少人.
(2024·汕头潮南质检)某次数学测试,抽取部分同学的成绩(得分为整数),整理制成如
图所示的频数分布直方图,根据图示信息描述不正确的是( )
A.频数分布直方图中组距是10
B.本次抽样样本容量是60
C.70.5~80.5这一分数段的频数为18
D.估计这次数学测试及格(不低于60
分)率为92%
B
1.(2024·云浮新兴期中)统计得到一组数据最大值为145,最小值为30,取组距为20,可
分成( )
A.3组 B.4组 C.5组 D.6组
【解析】在样本数据中最大值为145,最小值为30,它们的差是145-30=115,
已知组距为20,由于115÷20≈6,故可以分成6组.
D
2.(2024·汕头潮南质检)某学校随机抽取了400名学生的测试成绩作为样本,数据整理
如表所示,则等级为A和B的共有________人.
等级 A B C D
频数 150 4
频率 0.18
324
3.为了普及足球运动的有关知识,某校举办了一场关于足球运动的知识竞赛.为了解此次知识竞赛成绩的情况,随机抽取了部分参赛学生的成绩,得到频数分布直方图,如图(每组含前一个边界值,不含后一个边界值).请根据该直方图,回答下列问题:
(1)数据分组时的组距为________分.
(2)自左至右分别为第1,2,3,4组,频数最大的是哪一组
(3)学校决定为成绩在80分以上(包括80分)的学生颁发优秀证书,若该校共有800名学生,请估计能拿到优秀证书的学生人数.
C
12
知识点2 频数分布表与直方图
3.某班将安全知识竞赛成绩整理后绘制成频数分布直方图,图中从左至右前四组的
百分比分别是4%,12%,40%,28%,第五组的频数是8,下列结论中错误的是( )
A.80分以上的学生有14名
B.该班有50名同学参赛
C.成绩在70~80分的人数最多
D.第五组的百分比为16%
A
【解析】该班参赛的学生有8÷(1-4%-12%-40%-28%)=50(名),故选项B说法正确;
80分以上的学生有50×28%+8=22(名),故选项A说法错误;成绩在70~80分的人数最多,故选项C说法正确;
第五组的百分比为8÷50×100%=16%,故选项D说法正确.
B
5.(易错警示题·隐含条件未挖掘)某中学七年级甲、乙、丙三个班中,每班的学生人数都为40,某次数学考试的成绩统计如图表所示(每组分数含最小值,不含最大值).根据图表提供的信息﹐则80≤x<90分这一组人数最多的班是_________.
丙班数学成绩频数统计表
分数 50≤x
<60 60≤x
<70 70≤x
<80 80≤x
<90 90≤x
<100
人数 1 4 15 11 9
甲班
【解析】由甲班数学成绩频数分布直方图可知,80≤x<90分这一组人数大于12,由乙班数学成绩各分数段人数统计图可知,80≤x<90分这一组人数是40×(1-10%-5%-35%-20%)=12,由丙班数学成绩频数统计表可知,80≤x<90分这一组人数是11,所以甲班在80≤x<90分这一组人数最多.
6.(应用意识)
如图为国家节水标志,节水标志各部分的含义为:圆形代表地球,标志留白部分像一只手托起一滴水,手又像一条蜿蜒的河流,象征滴水汇成江河.某市在实施居民用水定额管理前,对居民生活用水情况进行了调查,通过简单随机抽样调查获得了50个家庭去年的月均用水量(单位:吨).以下是整理数据后的不完整图表.
月均用水量频数分布表
分组 频数
2≤x<3 4
3≤x<4 12
4≤x<5 a
5≤x<6 9
6≤x<7 5
7≤x<8 4
8≤x<9 2
合计 50
请根据图表中提供的信息解答下列问题:
(1)表中a的值为________,请补全频数分布直方图;
(2)在扇形图中,月均用水量为“E:6≤x<7”的扇形的圆心角是________°;
(3)为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费.若要使60%的家庭水费支出不受影响,你觉得家庭月均用水量应该定为多少 为什么
同课章节目录
