11.2 一元一次不等式 第2课时 课件(共24张PPT)
文档属性
| 名称 | 11.2 一元一次不等式 第2课时 课件(共24张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 00:00:00 | ||
图片预览








文档简介
(共24张PPT)
11.2 一元一次不等式
第2课时
课时目标 素养达成
1.能用一元一次不等式解决实际问题 应用意识
2.能用一元一次不等式解决方案问题 抽象能力、应用意识
列不等式解应用题的一般步骤
(1)审:分清已知量与未知量及其关系,找到题目中的_________关系,要抓住题中“大
于”“不大于”“至少”“不超过”等关键字及其含义.
(2)设:设出适当的___________.
(3)列:根据题中的不等关系,列出___________.
(4)解:解这个___________.
(5)验:检验是否符合实际问题.
(6)答:作答.
不等
未知数
不等式
不等式
1.某次知识竞赛共有25道题,每答对一题得5分,答错或不答都扣2分.小明得分要超过
90分,他至少要答对多少道题 如果设小明答对x道题,那么他答错或不答的题数为
(25-x),根据题意,下列不等式中,正确的是( )
A.5x-2(25-x)≥90 B.5x-2(25-x)≤90
C.5x-2(25-x)>90 D.5x-2(25-x)<90
2.七年级(1)班学生郊游后合影留念,照相馆冲洗胶片需22.5元,洗一张照片需用2.5元.
如果每人洗一张照片,且每人付款不超过3元,那么这个班至少有_______名学生.
C
45
【典例1】(教材再开发·P133例2强化)为响应乡村振兴号召,在外地创业成功的大学毕业生李小华毅然返乡当起了新农人,创办了蔬菜生态种植基地.最近,为给基地的蔬菜施肥,李小华准备购买甲、乙两种有机肥,已知甲种有机肥每吨的价格比乙种有机肥每吨的价格多120元,购买2吨甲种有机肥和1吨乙种有机肥共需1 830元.
(1)甲、乙两种有机肥每吨各多少元
(2)若李小华准备购买甲、乙两种有机肥共10吨,且总费用不能超过5 660元,则李小华最多能购买甲种有机肥多少吨
一元一次不等式的应用(运算能力、应用意识)
(2024·惠州惠东期末)某种衬衫的进价为400元,出售时标价为550元.由于换季,商店准
备打折销售,但要保持利润不低于10%,那么至多打______折.
【解析】设该衬衫可打x折.
根据题意得550×0.1x-400≥400×10%,
解得x≥8,
即该衬衫至多打八折.
8
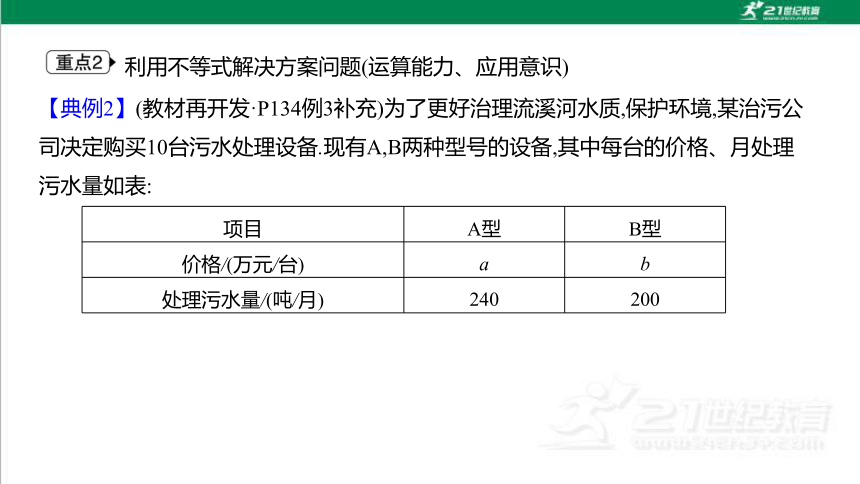
【典例2】(教材再开发·P134例3补充)为了更好治理流溪河水质,保护环境,某治污公司决定购买10台污水处理设备.现有A,B两种型号的设备,其中每台的价格、月处理污水量如表:
利用不等式解决方案问题(运算能力、应用意识)
项目 A型 B型
价格/(万元/台) a b
处理污水量/(吨/月) 240 200
经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
(1)求a,b的值.
(2)经预算:该治污公司购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案
(3)在(2)的条件下,若每月要求处理流溪河两岸的污水量不低于2 040吨,为了节约资金,请你为该治污公司设计一种最省钱的购买方案.
某工厂为了扩大生产,决定购买6台机器用于生产零件,现有甲、乙两种型号机器可供选择,经调查,购买3台甲型机器和2台乙型机器共需要31万元,购买1台甲型机器比购买1台乙型机器多2万元,
(1)求甲、乙两种型号机器每台各多少万元;
(2)如果该工厂购买机器的预算资金不超过34万元,那么你认为该工厂购买甲型机器有多少种方案
A
8
知识点1 一元一次不等式的应用
1.某学校组织七年级学生到劳动实践教育基地参加实践活动,某小组的任务是平整土地
600m2,学校要求完成全部任务的时间不超过3小时.开始的半小时,由于操作不熟练,只平整了
60m2.若设他们在剩余时间内每小时平整土地xm2,则根据题意可列不等式为( )
A.60+(3-0.5)x≥600
B.60+(3-0.5)x≤600
C.600-60x-0.5≤3
D.0.5+600-60x≥3
【解析】他们在剩余时间内每小时平整土地xm2,由题意得:60+(3-0.5)x≥600.
A
知识点2 利用不等式解决方案问题
2.某单位为响应政府号召,为“创城工作”贡献力量,需要购买分类垃圾桶8个,市场上有
A型和B型两种分类垃圾桶,A型分类垃圾桶150元/个,B型分类垃圾桶225元/个.若总
费用不超过1 500元,则不同的购买方案有( )
A.7种 B.6种 C.5种 D.4种
【解析】设购买A型分类垃圾桶x个,则购买B型分类垃圾桶(8-x)个.
由题意得:150x+225(8-x)≤1 500,
解得x≥4.
∵x,8-x均为非负整数,∴x=4,5,6,7,8,
∴共有5种购买方案.
C
3.某公司推出两种移动电话收费方案.方案一:月租费36元,本地通话话费0.1元/分;方
案二:不收月租费,本地通话费为0.6元/分.设小明的爸爸一个月通话时间为x分钟.小
明的爸爸一个月通话时间为________时,选择方案一比方案二优惠.( )
A.60分钟 B.70分钟
C.72分钟 D.80分钟
【解析】小明的爸爸一个月通话时间为x分钟.方案一费用:36+0.1x,方案二费用:0.6x.
当方案一比方案二优惠时,36+0.1x<0.6x,
解得x>72.
D
C
5.把一些书分给几名同学,若每人分9本,则书本有剩余,条件*.若根据题意,设有x名同
学,可得到符合题意的不等式5(x+3)>9x,则“条件*”可以是( )
A.每人分5本,则剩余3本
B.每人分5本,则剩余的书可多分给3个人
C.每人分5本,则还差3本
D.其中一个人分5本,则其他同学每人可分3本
【解析】∵5(x+3)>9x,每人分9本,有x名同学,
∴每人分5本,则剩余的书可多分给3个人.
B
6.某工程队计划在5天内修路6 km,施工第一天修完1.2 km,计划发生变化,需至少提前
1天完成修路任务,则后期每天至少修路_______km.
【解析】设后期每天修路x km.依题意有:1.2+(5-1-1)x≥6,解得x≥1.6.故后期每天至少
修路1.6 km.
1.6
7.(应用意识)骑行过程中佩戴安全头盔,可以保护头部,减少伤害.某商店经销甲、乙两种安全头盔,近两天的销售情况如表.
时间 甲种安全头盔销量/个 乙种安全头盔销量/个 销售额/元
第一天 10 15 1 150
第二天 6 12 810
(1)求甲、乙两种安全头盔的销售单价.
(2)若甲、乙两种安全头盔的进价分别为40元/个、30元/个,商店准备用不超过3 400元的资金,再购进这两种安全头盔共100个.
①最多能购进甲种安全头盔多少个
②商店销售完这100个安全头盔能否实现利润为1 300元的目标 若能,请给出相应的进货方案;若不能,请说明理由.(注:利润=售价-进价,进价、售价均保持不变)
②不能实现利润为1 300元的目标.理由如下:
设购进甲种安全头盔a个,则购进乙种安全头盔(100-a)个.
依题意得(55-40)a+(40-30)(100-a)=1 300,解得a=60.又由①知甲种安全头盔最多购进40个,所以不能实现利润为1 300元的目标.
11.2 一元一次不等式
第2课时
课时目标 素养达成
1.能用一元一次不等式解决实际问题 应用意识
2.能用一元一次不等式解决方案问题 抽象能力、应用意识
列不等式解应用题的一般步骤
(1)审:分清已知量与未知量及其关系,找到题目中的_________关系,要抓住题中“大
于”“不大于”“至少”“不超过”等关键字及其含义.
(2)设:设出适当的___________.
(3)列:根据题中的不等关系,列出___________.
(4)解:解这个___________.
(5)验:检验是否符合实际问题.
(6)答:作答.
不等
未知数
不等式
不等式
1.某次知识竞赛共有25道题,每答对一题得5分,答错或不答都扣2分.小明得分要超过
90分,他至少要答对多少道题 如果设小明答对x道题,那么他答错或不答的题数为
(25-x),根据题意,下列不等式中,正确的是( )
A.5x-2(25-x)≥90 B.5x-2(25-x)≤90
C.5x-2(25-x)>90 D.5x-2(25-x)<90
2.七年级(1)班学生郊游后合影留念,照相馆冲洗胶片需22.5元,洗一张照片需用2.5元.
如果每人洗一张照片,且每人付款不超过3元,那么这个班至少有_______名学生.
C
45
【典例1】(教材再开发·P133例2强化)为响应乡村振兴号召,在外地创业成功的大学毕业生李小华毅然返乡当起了新农人,创办了蔬菜生态种植基地.最近,为给基地的蔬菜施肥,李小华准备购买甲、乙两种有机肥,已知甲种有机肥每吨的价格比乙种有机肥每吨的价格多120元,购买2吨甲种有机肥和1吨乙种有机肥共需1 830元.
(1)甲、乙两种有机肥每吨各多少元
(2)若李小华准备购买甲、乙两种有机肥共10吨,且总费用不能超过5 660元,则李小华最多能购买甲种有机肥多少吨
一元一次不等式的应用(运算能力、应用意识)
(2024·惠州惠东期末)某种衬衫的进价为400元,出售时标价为550元.由于换季,商店准
备打折销售,但要保持利润不低于10%,那么至多打______折.
【解析】设该衬衫可打x折.
根据题意得550×0.1x-400≥400×10%,
解得x≥8,
即该衬衫至多打八折.
8
【典例2】(教材再开发·P134例3补充)为了更好治理流溪河水质,保护环境,某治污公司决定购买10台污水处理设备.现有A,B两种型号的设备,其中每台的价格、月处理污水量如表:
利用不等式解决方案问题(运算能力、应用意识)
项目 A型 B型
价格/(万元/台) a b
处理污水量/(吨/月) 240 200
经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
(1)求a,b的值.
(2)经预算:该治污公司购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案
(3)在(2)的条件下,若每月要求处理流溪河两岸的污水量不低于2 040吨,为了节约资金,请你为该治污公司设计一种最省钱的购买方案.
某工厂为了扩大生产,决定购买6台机器用于生产零件,现有甲、乙两种型号机器可供选择,经调查,购买3台甲型机器和2台乙型机器共需要31万元,购买1台甲型机器比购买1台乙型机器多2万元,
(1)求甲、乙两种型号机器每台各多少万元;
(2)如果该工厂购买机器的预算资金不超过34万元,那么你认为该工厂购买甲型机器有多少种方案
A
8
知识点1 一元一次不等式的应用
1.某学校组织七年级学生到劳动实践教育基地参加实践活动,某小组的任务是平整土地
600m2,学校要求完成全部任务的时间不超过3小时.开始的半小时,由于操作不熟练,只平整了
60m2.若设他们在剩余时间内每小时平整土地xm2,则根据题意可列不等式为( )
A.60+(3-0.5)x≥600
B.60+(3-0.5)x≤600
C.600-60x-0.5≤3
D.0.5+600-60x≥3
【解析】他们在剩余时间内每小时平整土地xm2,由题意得:60+(3-0.5)x≥600.
A
知识点2 利用不等式解决方案问题
2.某单位为响应政府号召,为“创城工作”贡献力量,需要购买分类垃圾桶8个,市场上有
A型和B型两种分类垃圾桶,A型分类垃圾桶150元/个,B型分类垃圾桶225元/个.若总
费用不超过1 500元,则不同的购买方案有( )
A.7种 B.6种 C.5种 D.4种
【解析】设购买A型分类垃圾桶x个,则购买B型分类垃圾桶(8-x)个.
由题意得:150x+225(8-x)≤1 500,
解得x≥4.
∵x,8-x均为非负整数,∴x=4,5,6,7,8,
∴共有5种购买方案.
C
3.某公司推出两种移动电话收费方案.方案一:月租费36元,本地通话话费0.1元/分;方
案二:不收月租费,本地通话费为0.6元/分.设小明的爸爸一个月通话时间为x分钟.小
明的爸爸一个月通话时间为________时,选择方案一比方案二优惠.( )
A.60分钟 B.70分钟
C.72分钟 D.80分钟
【解析】小明的爸爸一个月通话时间为x分钟.方案一费用:36+0.1x,方案二费用:0.6x.
当方案一比方案二优惠时,36+0.1x<0.6x,
解得x>72.
D
C
5.把一些书分给几名同学,若每人分9本,则书本有剩余,条件*.若根据题意,设有x名同
学,可得到符合题意的不等式5(x+3)>9x,则“条件*”可以是( )
A.每人分5本,则剩余3本
B.每人分5本,则剩余的书可多分给3个人
C.每人分5本,则还差3本
D.其中一个人分5本,则其他同学每人可分3本
【解析】∵5(x+3)>9x,每人分9本,有x名同学,
∴每人分5本,则剩余的书可多分给3个人.
B
6.某工程队计划在5天内修路6 km,施工第一天修完1.2 km,计划发生变化,需至少提前
1天完成修路任务,则后期每天至少修路_______km.
【解析】设后期每天修路x km.依题意有:1.2+(5-1-1)x≥6,解得x≥1.6.故后期每天至少
修路1.6 km.
1.6
7.(应用意识)骑行过程中佩戴安全头盔,可以保护头部,减少伤害.某商店经销甲、乙两种安全头盔,近两天的销售情况如表.
时间 甲种安全头盔销量/个 乙种安全头盔销量/个 销售额/元
第一天 10 15 1 150
第二天 6 12 810
(1)求甲、乙两种安全头盔的销售单价.
(2)若甲、乙两种安全头盔的进价分别为40元/个、30元/个,商店准备用不超过3 400元的资金,再购进这两种安全头盔共100个.
①最多能购进甲种安全头盔多少个
②商店销售完这100个安全头盔能否实现利润为1 300元的目标 若能,请给出相应的进货方案;若不能,请说明理由.(注:利润=售价-进价,进价、售价均保持不变)
②不能实现利润为1 300元的目标.理由如下:
设购进甲种安全头盔a个,则购进乙种安全头盔(100-a)个.
依题意得(55-40)a+(40-30)(100-a)=1 300,解得a=60.又由①知甲种安全头盔最多购进40个,所以不能实现利润为1 300元的目标.
同课章节目录
