11.2 一元一次不等式 第1课时 课件(共26张PPT)
文档属性
| 名称 | 11.2 一元一次不等式 第1课时 课件(共26张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 21:36:18 | ||
图片预览







文档简介
(共26张PPT)
11.2 一元一次不等式
第1课时
课时目标 素养达成
1.了解一元一次不等式的概念 抽象能力
2.能解一元一次不等式 运算能力、模型概念
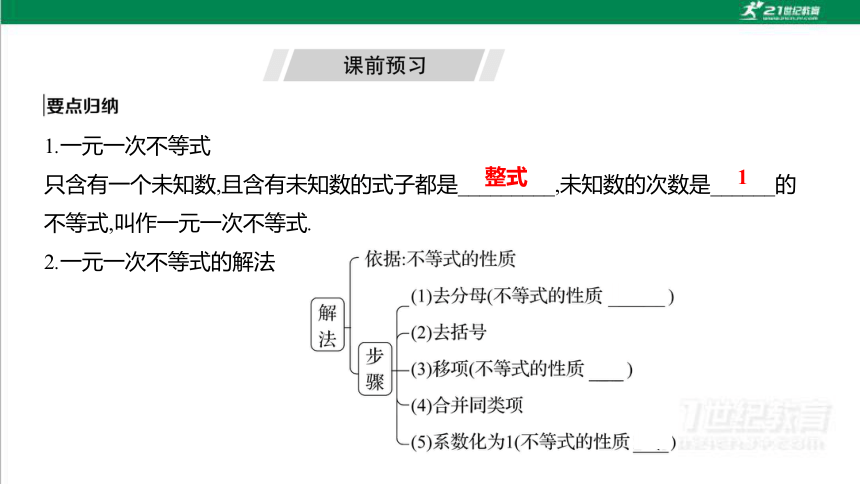
1.一元一次不等式
只含有一个未知数,且含有未知数的式子都是_________,未知数的次数是______的
不等式,叫作一元一次不等式.
2.一元一次不等式的解法
整式
1
B
C
-2
【典例1】(教材再开发·P131思考强化)
已知(a-4)x|3-a|+1>0是关于x的一元一次不等式,求a的值.
【自主解答】根据题意,得|3-a|=1,且a-4≠0,∴a=2.
一元一次不等式的概念(抽象能力、模型观念)
B
2.(2024·揭阳榕城期末)若(m-2)x|m-1|-3>6是关于x的一元一次不等式,则m=______.
【解析】根据题意,
得|m-1|=1且m-2≠0,
解得m=0.
0
一元一次不等式的解法(运算能力、模型观念)
1.已知(k+3)x|k|-2+5A.x<1 B.x<-1
C.x<2 D.x>-1
【解析】由题意得,|k|-2=1且k+3≠0,解得k=3,
∴不等式为6x+5<3-4,解得x<-1.
B
【解析】去分母,得3(x+5)-2(2x+3)≥12,
去括号,得3x+15-4x-6≥12,
移项,得3x-4x≥12-15+6,
合并同类项,得-x≥3,
系数化为1,得x≤-3.
不等式的解集在数轴上表示如图.
D
x>2
C
2.若(n-2)yn-3+29>0是关于y的一元一次不等式,则n的值为______.
【解析】∵(n-2)yn-3+29>0是关于y的一元一次不等式,
∴n-3=1且n-2≠0,解得n=4.
4
D
C
5.(2024·湛江赤坎期末)不等式3x-5<3+x的非负整数解有______个.
【解析】移项,得3x-x<3+5,
合并同类项,得2x<8,
系数化为1,得x<4,
则此不等式的非负整数解有0,1,2,3,共4个.
4
8.已知m是不等式5x-2≥3的解,而n不是5x-2≥3的解,则( )
A.m>n B.m【解析】解不等式5x-2≥3,得x≥1.
∵m是不等式的解,n不是不等式的解,
∴m≥1,n<1∴m>n.
9.若不等式mx-n>0的解集为x<1,则不等式mx-2m-n>0的解集为( )
A.x<1 B.x>1 C.x<3 D.x>3
【解析】解不等式mx-n>0,得解集为x<1,
∴m<0,且m=n,∵mx-2m-n>0,
∴mx>2m+n,∴mx>3m,∴x<3.
A
C
k<3
(2)∵x-2>mn,∴x>2+mn.
∵x-4>0,
∴x>4,∵不等式C:x-2>mn与不等式D:x-4>0是同解不等式,
∴2+mn=4,
∴mn=2.
∵m,n是整数,∴m=1,n=2或m=-1,n=-2或m=2,n=1或m=-2,n=-1.
11.2 一元一次不等式
第1课时
课时目标 素养达成
1.了解一元一次不等式的概念 抽象能力
2.能解一元一次不等式 运算能力、模型概念
1.一元一次不等式
只含有一个未知数,且含有未知数的式子都是_________,未知数的次数是______的
不等式,叫作一元一次不等式.
2.一元一次不等式的解法
整式
1
B
C
-2
【典例1】(教材再开发·P131思考强化)
已知(a-4)x|3-a|+1>0是关于x的一元一次不等式,求a的值.
【自主解答】根据题意,得|3-a|=1,且a-4≠0,∴a=2.
一元一次不等式的概念(抽象能力、模型观念)
B
2.(2024·揭阳榕城期末)若(m-2)x|m-1|-3>6是关于x的一元一次不等式,则m=______.
【解析】根据题意,
得|m-1|=1且m-2≠0,
解得m=0.
0
一元一次不等式的解法(运算能力、模型观念)
1.已知(k+3)x|k|-2+5
C.x<2 D.x>-1
【解析】由题意得,|k|-2=1且k+3≠0,解得k=3,
∴不等式为6x+5<3-4,解得x<-1.
B
【解析】去分母,得3(x+5)-2(2x+3)≥12,
去括号,得3x+15-4x-6≥12,
移项,得3x-4x≥12-15+6,
合并同类项,得-x≥3,
系数化为1,得x≤-3.
不等式的解集在数轴上表示如图.
D
x>2
C
2.若(n-2)yn-3+29>0是关于y的一元一次不等式,则n的值为______.
【解析】∵(n-2)yn-3+29>0是关于y的一元一次不等式,
∴n-3=1且n-2≠0,解得n=4.
4
D
C
5.(2024·湛江赤坎期末)不等式3x-5<3+x的非负整数解有______个.
【解析】移项,得3x-x<3+5,
合并同类项,得2x<8,
系数化为1,得x<4,
则此不等式的非负整数解有0,1,2,3,共4个.
4
8.已知m是不等式5x-2≥3的解,而n不是5x-2≥3的解,则( )
A.m>n B.m
∵m是不等式的解,n不是不等式的解,
∴m≥1,n<1∴m>n.
9.若不等式mx-n>0的解集为x<1,则不等式mx-2m-n>0的解集为( )
A.x<1 B.x>1 C.x<3 D.x>3
【解析】解不等式mx-n>0,得解集为x<1,
∴m<0,且m=n,∵mx-2m-n>0,
∴mx>2m+n,∴mx>3m,∴x<3.
A
C
k<3
(2)∵x-2>mn,∴x>2+mn.
∵x-4>0,
∴x>4,∵不等式C:x-2>mn与不等式D:x-4>0是同解不等式,
∴2+mn=4,
∴mn=2.
∵m,n是整数,∴m=1,n=2或m=-1,n=-2或m=2,n=1或m=-2,n=-1.
同课章节目录
