10.4 三元一次方程组的解法 课件(共39张PPT)
文档属性
| 名称 | 10.4 三元一次方程组的解法 课件(共39张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 21:40:49 | ||
图片预览











文档简介
(共39张PPT)
*10.4 三元一次方程组的解法
课时目标 素养达成
1.能解简单的三元一次方程组 模型观念、运算能力
2.会用三元一次方程组解决实际问题 应用意识
1.三元一次方程组
(1)这个方程组共有_______个未知数.
(2)含有未知数的式子都是_________.
(3)所含有未知数的项的次数都是______.
2.三元一次方程组的解法
(1)基本思路:“三元”化为“_________”,进而再转化为“_________”.
(2)一般步骤:选→化→解→求→得.
3.三元一次方程组的应用
一般步骤:找等量关系→设未知数→列方程组
→解方程组→检验→写出答案.
三
整式
1
二元
一元
C
B
180
三元一次方程组的解法(模型观念、运算能力)
C
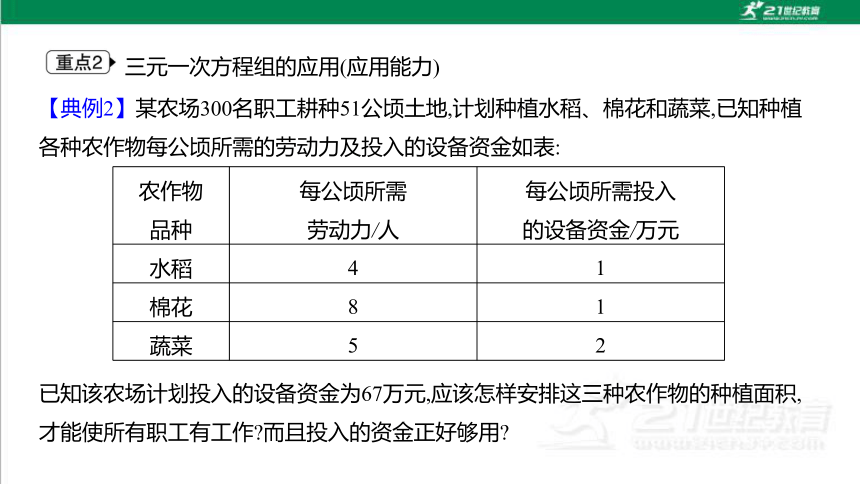
【典例2】某农场300名职工耕种51公顷土地,计划种植水稻、棉花和蔬菜,已知种植各种农作物每公顷所需的劳动力及投入的设备资金如表:
三元一次方程组的应用(应用能力)
农作物
品种 每公顷所需
劳动力/人 每公顷所需投入
的设备资金/万元
水稻 4 1
棉花 8 1
蔬菜 5 2
已知该农场计划投入的设备资金为67万元,应该怎样安排这三种农作物的种植面积,才能使所有职工有工作 而且投入的资金正好够用
某超市在促销活动中准备了三种小礼品共16件,16件小礼品的总价为50元,三种小礼品的价格分别为2元/件、4元/件和10元/件,每种小礼品至少准备1件.已知价格为2元/件的小礼品有a件.
(1)请用含a的式子分别表示准备的另外两种小礼品的件数;
(2)如果准备价格为2元/件的小礼品的数量正好是价格为4元/件的小礼品的2倍,分别求出准备的三种价格小礼品的件数.
B
A
2
C
A
B
24
8.水果市场将120吨水果运往各地商家,现有甲、乙、丙三种车型供选择,每辆车的运载量和运费如表所示(假设每辆车均满载):
车型 甲 乙 丙
汽车运载量/(吨/辆) 5 8 10
汽车运费/(元/辆) 400 500 600
(1)若全部水果都用甲、乙两种车型来运送,需运费8 200元,则分别需甲、乙两种车型各多少辆
(2)为了节约运费,市场可以调用甲、乙、丙三种车型参与运送(每种车型至少1辆),已知它们的总辆数为16辆,市场的运送方案有哪几种
综合与实践活动
方程解与点坐标关系的探索
教材P115【数学活动】活动1
二元一次方程的“图象”
【描述定义】以关于x,y的方程ax+by=0的解为坐标的点的全体叫作方程ax+by=0的图象.
【活动目的】通过解二元一次方程(组)、找出坐标系中的点,猜想方程的解与点坐标的关系.
无数
(1,2)
(3,6)
用二元一次方程解得的x,y的值分别作为点的横、纵坐标,则该点一定在直
线AB上
(5)在直线AB上,找出其中的一些点,确定这些点的坐标,并用这些点的横坐标代入方
程中的x,用这些点的纵坐标代入方程中的y,判断这组数值是否为方程的解.
归纳:
①_____________________________________________________________________
______________________;
②_____________________________________________________________________
_________.
以关于x,y的方程ax+by=0的解为坐标的点的全体组成了一条直线,这条直线就
是方程ax+by=0的图象
方程ax+by=0的图象上的任何一个点的横、纵坐标就是方程ax+by=0的一个解
的x,y值
1.如图,关于x,y的方程y=kx+b与y=x+2的图象相交于点P(m,4),则关于x的方程kx+b=4
的解是( )
A.x=1 B.x=2
C.x=3 D.x=4
【解析】∵图象相交于点P(m,4),∴将P(m,4)代入y=x+2中,得出m+2=4,解得m=2,
∴P点坐标为(2,4).根据图象可知,函数y=kx+b与y=x+2的图象相交于点P(2,4),
∴当x=2时,y=kx+b=4.
B
A
*10.4 三元一次方程组的解法
课时目标 素养达成
1.能解简单的三元一次方程组 模型观念、运算能力
2.会用三元一次方程组解决实际问题 应用意识
1.三元一次方程组
(1)这个方程组共有_______个未知数.
(2)含有未知数的式子都是_________.
(3)所含有未知数的项的次数都是______.
2.三元一次方程组的解法
(1)基本思路:“三元”化为“_________”,进而再转化为“_________”.
(2)一般步骤:选→化→解→求→得.
3.三元一次方程组的应用
一般步骤:找等量关系→设未知数→列方程组
→解方程组→检验→写出答案.
三
整式
1
二元
一元
C
B
180
三元一次方程组的解法(模型观念、运算能力)
C
【典例2】某农场300名职工耕种51公顷土地,计划种植水稻、棉花和蔬菜,已知种植各种农作物每公顷所需的劳动力及投入的设备资金如表:
三元一次方程组的应用(应用能力)
农作物
品种 每公顷所需
劳动力/人 每公顷所需投入
的设备资金/万元
水稻 4 1
棉花 8 1
蔬菜 5 2
已知该农场计划投入的设备资金为67万元,应该怎样安排这三种农作物的种植面积,才能使所有职工有工作 而且投入的资金正好够用
某超市在促销活动中准备了三种小礼品共16件,16件小礼品的总价为50元,三种小礼品的价格分别为2元/件、4元/件和10元/件,每种小礼品至少准备1件.已知价格为2元/件的小礼品有a件.
(1)请用含a的式子分别表示准备的另外两种小礼品的件数;
(2)如果准备价格为2元/件的小礼品的数量正好是价格为4元/件的小礼品的2倍,分别求出准备的三种价格小礼品的件数.
B
A
2
C
A
B
24
8.水果市场将120吨水果运往各地商家,现有甲、乙、丙三种车型供选择,每辆车的运载量和运费如表所示(假设每辆车均满载):
车型 甲 乙 丙
汽车运载量/(吨/辆) 5 8 10
汽车运费/(元/辆) 400 500 600
(1)若全部水果都用甲、乙两种车型来运送,需运费8 200元,则分别需甲、乙两种车型各多少辆
(2)为了节约运费,市场可以调用甲、乙、丙三种车型参与运送(每种车型至少1辆),已知它们的总辆数为16辆,市场的运送方案有哪几种
综合与实践活动
方程解与点坐标关系的探索
教材P115【数学活动】活动1
二元一次方程的“图象”
【描述定义】以关于x,y的方程ax+by=0的解为坐标的点的全体叫作方程ax+by=0的图象.
【活动目的】通过解二元一次方程(组)、找出坐标系中的点,猜想方程的解与点坐标的关系.
无数
(1,2)
(3,6)
用二元一次方程解得的x,y的值分别作为点的横、纵坐标,则该点一定在直
线AB上
(5)在直线AB上,找出其中的一些点,确定这些点的坐标,并用这些点的横坐标代入方
程中的x,用这些点的纵坐标代入方程中的y,判断这组数值是否为方程的解.
归纳:
①_____________________________________________________________________
______________________;
②_____________________________________________________________________
_________.
以关于x,y的方程ax+by=0的解为坐标的点的全体组成了一条直线,这条直线就
是方程ax+by=0的图象
方程ax+by=0的图象上的任何一个点的横、纵坐标就是方程ax+by=0的一个解
的x,y值
1.如图,关于x,y的方程y=kx+b与y=x+2的图象相交于点P(m,4),则关于x的方程kx+b=4
的解是( )
A.x=1 B.x=2
C.x=3 D.x=4
【解析】∵图象相交于点P(m,4),∴将P(m,4)代入y=x+2中,得出m+2=4,解得m=2,
∴P点坐标为(2,4).根据图象可知,函数y=kx+b与y=x+2的图象相交于点P(2,4),
∴当x=2时,y=kx+b=4.
B
A
同课章节目录
