七年级上册人民教育出版社5.2.2 解一元一次方程-移项(共18张PPT)
文档属性
| 名称 | 七年级上册人民教育出版社5.2.2 解一元一次方程-移项(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 09:41:20 | ||
图片预览





文档简介
(共18张PPT)
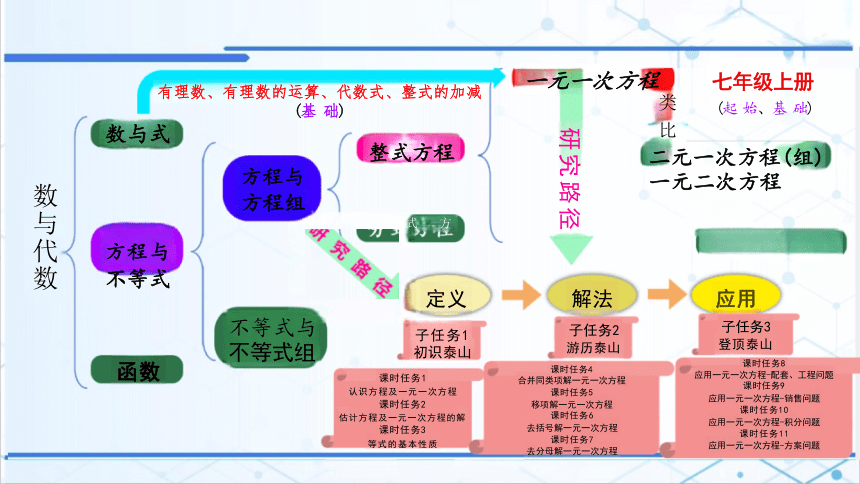
初中数学 七年级上册 人民教育出版社
5.2.2 解一元一次方程—移项
有理数、有理数的运算、代数式、整式的加减
(基 础)
整式方程
方程与
方程组
分 式 方 程
方程与
不等式
二元一次方程(组)一元二次方程
子任务3
登顶泰山
课时任务8
应用一元一次方程-配套、工程问题
课时任务9
应用一元一次方程-销售问题
课时任务10
应用一元一次方程-积分问题
课时任务11
应用一元一次方程-方案问题
子任务1 初识泰山
课时任务1
认识方程及一元一次方程
课时任务2
估计方程及一元一次方程的解
课时任务3
等式的基本性质
子任务2
游历泰山
课时任务4
合并同类项解一元一次方程
课时任务5
移项解一元一次方程 课时任务6
去括号解一元一次方程
课时任务7
去分母解一元一次方程
一元一次方程 七年级上册
(起 始、基 础)
定义 解法 应用
不等式与 不等式组
数与代数
研究路径
数与式
函数
类 比
1.能根据等式的基本性质,把形如 “ax+b=cx+d” 的一
元一次方程,化成 “x=m ( 其中m为常数)”的形式, 发展化归思想;
2.经历解形如ax+b=cx+d 的一元一次方程的过程,能
归纳出用“移项”解一元一次方程的步骤,发展运算 能 力 ;
3.能根据具体问题中的数量关系列出一元一次方程,
并能解出方程的解,发展抽象能力和方程模型观念。
学 习 目 标
1.解方程的目标是把方程转化为:x=m (其中m 为常数)的形 式。
2.解方程 2x-2.5x=6-8
同回顾
甲、乙两个研学团队沿同一路线同时向泰山山顶进
发. 甲队从距红门的1km的一号集合地出发,每小时
行进1.2km; 乙队从距红门3km的二号集合地出发,每 小时行进0.8km. 多长时间后,甲队在途中追上乙队
解:设经过x小时后,甲队在途中追上乙队
1.2x+1=0.8x+3
Heaven srect
南天门
South Gate
to Heaven
升仙坊
Shengxdan
N
Egencs
对松山
Pinetree Valley
朝阳洞
Chaoyang Gave
望人松
Expecting Guests Pine
五大夫松
Wudatu Pine
云步桥
Yunbu Bridge
中天门
中天门索道站 HalfHeyrente
Haliway Gate to Heaven
K柏 洞号集合地
cypress Cave
总理奉安纪念碑
Monument Of Premier
Sun Yatsen
经 石 峪
Jingshi Valley
一号集合地
革命烈士纪念碑
Monument of the
虎山公园
王母池
Wangmu Pool
岱宗坊
DaizongAciway
岱 庙
Da Tempte
Bixia
孔子庙
Confucus Temple 神憩宾 Shenqi Hok
红 门
同回顾
玉lad 顶
日观峰
Sun Watching
Peak
Temple
太
孔子登临处
sehev
月观峰
Moon eatkching
Revolutionary Martyrs
北
万仙楼
碧霞祠
天街
探究: 时间:3分钟
方程1.2x+1=0.8x+3的两边都含有x的项(1.2x和0.8x) 和不含字母的常数
项(+1和+3),怎样才能转化为x=m (常数)的形式呢
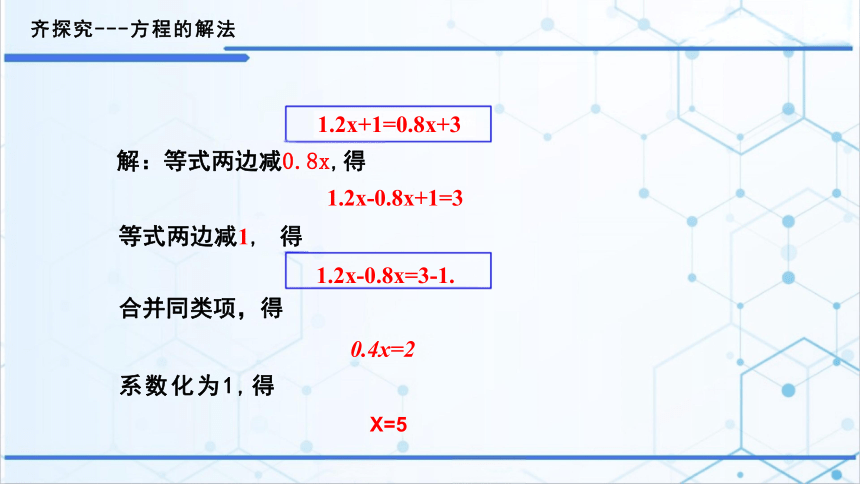
齐探究---方程的解法
齐探究---方程的解法
1.2x+1=0.8x+3 解:等式两边减0.8x,得
1.2x-0.8x+1=3
等式两边减1, 得
1.2x-0.8x=3-1.
合并同类项,得
0.4x=2
系数化为1,得
X=5
像这样把等式一边的某项
变号后移到另一边,叫做移项.
“移项”有"两变化":
(1)位置变化:从方程的 一边移到方程的另一边.
(2)符号变化:由正变负, 负变正.
齐探究---方程的解法
原方程:1.2 x+1=0.8x+3
变形后:1.2x-0.8x=3-1
下列方程的变形,属于移项的是( D )
A. 由- 3x=24得 x=-8
B.由 3x+6-2x=8得 3x-2x+6=8
C.由4x+5=0得 - 4x-5=0
D.由2x+1=0 得 2x=-1
易错提醒:
移项是方程中的某 一项从方程的一边 移到另一边,不要 将其与加法的交换 律或等式的性质2弄 混淆.
同辨析---移项
同归纳 - - - 解决问题
解 :1.2 x+1=0.8x+3
移项,得
1.2x-0.8x=3-1
合并同类项,得
0.4x=2
系数化为1,得
X=5
答:经过5小时后,甲队在途中追上乙队.
约820年,阿拉伯数学家花拉子米著有《代数
学》(又称《还原与对消计算概要》),其中,“还
原”指的是“移项”,“对消”隐含着移项后合并同类 项,我国古代数学著作《九章算术》的“方程”章,更 早使用了“对消”和“还原”的方法.
数学知识—解方程
阿尔一花拉子米,乌兹别克
族著名数学家、天文学家、 地理学家.代数与算术的整 理者,被誉为“代数之父 ”.
变式练--- 求解方程
解下列方程:(4分钟)
(1)3x+7=32-2x
齐探究一建立模型(5分钟)
问 题 “岱宗夫如何 齐鲁青未了”,游览山上风景,泰山索道 也成为许多游客的首选路线,其中比较热门的索道有中天门索道和桃花 源索道。已知接待这批研学团队,乘坐桃花源索道的团队人数要比单圈 载客最大量少100人;乘坐中天门索道的团队人数比单圈载客最大量还 多200人。乘坐桃花源索道与中天门索道的团队人数之比为2:5,求乘坐 桃花源索道、中天门索道的团队人数各是多少
分析:因为桃花源索道与中天门索道的团队人数之比为2:5,所以
可设它们的乘坐人数分别为2x 人 和 5x 人,再根据它们与单圈载客最大 量之间的关系列方程.
解 :设乘坐中天门索道与桃花源索道的分别为 5 x 人 和 2x 人
根据与单圈载客最大量之间的关系,得
5x—200=2x+100.
移项,得 5x—2x=100+200.
合并同类项,得 3x=300.
系数化为1,得 X=100.
所以 2x=200, 5x=500.
答:乘坐中天门索道与桃花源索道的团队分别为200人和500人.
学以致用
善总结—课堂小结
通过本节课的学习,你的收获是------
当堂测—解方程
1. 解下列方程:(6分钟)
(1)3x=4x+3; (2)6x-8=4x;
(3)6y-7=4y-5;
2 .李明出生时父亲28岁,现在父亲的年龄是李明年龄的3倍, 求现在李明的年龄.
1.完成教材习题5.2 1,5,6题;
2.实践作业:“校园读书日”期间,请同学们作为“小志愿者”通过整理图书馆的 一批书籍,算出两名同学每分钟分别可以整理多少册 小组合作,运用方程的知
识,完成问题。需要多长时间才能共同完成
任务:(1)两名“小志愿者”整理一分钟书籍
(2)两名计时员,计时1分钟,并算出“小志愿者”各自完成的书籍量。
(3)两名分配员,将需要整理的书籍平均分成两份,从其中一份中拿出100
册,放到另一份中,效率快的同学整理大份。
(4)两名设计员:将实践问题,转化成数学方程问题,并组内合作解答。
课后作业
共 勉
本单元我们从现实情境初始泰山、游历泰山出发,学习了一
元一次方程的定义、解法。
通过本单元的学习,希望同学们都有“会当凌绝顶, 一览众
山小"的志气和豪气,克服困难,在学习过程中学会“ 用数学 的眼光观察现实世界"“用数学的思维思考现实世界”,最后 能达到“会用数学的语言表达现实世界”,从而达到我们自己 学习数学的顶峰。
初中数学 七年级上册 人民教育出版社
5.2.2 解一元一次方程—移项
有理数、有理数的运算、代数式、整式的加减
(基 础)
整式方程
方程与
方程组
分 式 方 程
方程与
不等式
二元一次方程(组)一元二次方程
子任务3
登顶泰山
课时任务8
应用一元一次方程-配套、工程问题
课时任务9
应用一元一次方程-销售问题
课时任务10
应用一元一次方程-积分问题
课时任务11
应用一元一次方程-方案问题
子任务1 初识泰山
课时任务1
认识方程及一元一次方程
课时任务2
估计方程及一元一次方程的解
课时任务3
等式的基本性质
子任务2
游历泰山
课时任务4
合并同类项解一元一次方程
课时任务5
移项解一元一次方程 课时任务6
去括号解一元一次方程
课时任务7
去分母解一元一次方程
一元一次方程 七年级上册
(起 始、基 础)
定义 解法 应用
不等式与 不等式组
数与代数
研究路径
数与式
函数
类 比
1.能根据等式的基本性质,把形如 “ax+b=cx+d” 的一
元一次方程,化成 “x=m ( 其中m为常数)”的形式, 发展化归思想;
2.经历解形如ax+b=cx+d 的一元一次方程的过程,能
归纳出用“移项”解一元一次方程的步骤,发展运算 能 力 ;
3.能根据具体问题中的数量关系列出一元一次方程,
并能解出方程的解,发展抽象能力和方程模型观念。
学 习 目 标
1.解方程的目标是把方程转化为:x=m (其中m 为常数)的形 式。
2.解方程 2x-2.5x=6-8
同回顾
甲、乙两个研学团队沿同一路线同时向泰山山顶进
发. 甲队从距红门的1km的一号集合地出发,每小时
行进1.2km; 乙队从距红门3km的二号集合地出发,每 小时行进0.8km. 多长时间后,甲队在途中追上乙队
解:设经过x小时后,甲队在途中追上乙队
1.2x+1=0.8x+3
Heaven srect
南天门
South Gate
to Heaven
升仙坊
Shengxdan
N
Egencs
对松山
Pinetree Valley
朝阳洞
Chaoyang Gave
望人松
Expecting Guests Pine
五大夫松
Wudatu Pine
云步桥
Yunbu Bridge
中天门
中天门索道站 HalfHeyrente
Haliway Gate to Heaven
K柏 洞号集合地
cypress Cave
总理奉安纪念碑
Monument Of Premier
Sun Yatsen
经 石 峪
Jingshi Valley
一号集合地
革命烈士纪念碑
Monument of the
虎山公园
王母池
Wangmu Pool
岱宗坊
DaizongAciway
岱 庙
Da Tempte
Bixia
孔子庙
Confucus Temple 神憩宾 Shenqi Hok
红 门
同回顾
玉lad 顶
日观峰
Sun Watching
Peak
Temple
太
孔子登临处
sehev
月观峰
Moon eatkching
Revolutionary Martyrs
北
万仙楼
碧霞祠
天街
探究: 时间:3分钟
方程1.2x+1=0.8x+3的两边都含有x的项(1.2x和0.8x) 和不含字母的常数
项(+1和+3),怎样才能转化为x=m (常数)的形式呢
齐探究---方程的解法
齐探究---方程的解法
1.2x+1=0.8x+3 解:等式两边减0.8x,得
1.2x-0.8x+1=3
等式两边减1, 得
1.2x-0.8x=3-1.
合并同类项,得
0.4x=2
系数化为1,得
X=5
像这样把等式一边的某项
变号后移到另一边,叫做移项.
“移项”有"两变化":
(1)位置变化:从方程的 一边移到方程的另一边.
(2)符号变化:由正变负, 负变正.
齐探究---方程的解法
原方程:1.2 x+1=0.8x+3
变形后:1.2x-0.8x=3-1
下列方程的变形,属于移项的是( D )
A. 由- 3x=24得 x=-8
B.由 3x+6-2x=8得 3x-2x+6=8
C.由4x+5=0得 - 4x-5=0
D.由2x+1=0 得 2x=-1
易错提醒:
移项是方程中的某 一项从方程的一边 移到另一边,不要 将其与加法的交换 律或等式的性质2弄 混淆.
同辨析---移项
同归纳 - - - 解决问题
解 :1.2 x+1=0.8x+3
移项,得
1.2x-0.8x=3-1
合并同类项,得
0.4x=2
系数化为1,得
X=5
答:经过5小时后,甲队在途中追上乙队.
约820年,阿拉伯数学家花拉子米著有《代数
学》(又称《还原与对消计算概要》),其中,“还
原”指的是“移项”,“对消”隐含着移项后合并同类 项,我国古代数学著作《九章算术》的“方程”章,更 早使用了“对消”和“还原”的方法.
数学知识—解方程
阿尔一花拉子米,乌兹别克
族著名数学家、天文学家、 地理学家.代数与算术的整 理者,被誉为“代数之父 ”.
变式练--- 求解方程
解下列方程:(4分钟)
(1)3x+7=32-2x
齐探究一建立模型(5分钟)
问 题 “岱宗夫如何 齐鲁青未了”,游览山上风景,泰山索道 也成为许多游客的首选路线,其中比较热门的索道有中天门索道和桃花 源索道。已知接待这批研学团队,乘坐桃花源索道的团队人数要比单圈 载客最大量少100人;乘坐中天门索道的团队人数比单圈载客最大量还 多200人。乘坐桃花源索道与中天门索道的团队人数之比为2:5,求乘坐 桃花源索道、中天门索道的团队人数各是多少
分析:因为桃花源索道与中天门索道的团队人数之比为2:5,所以
可设它们的乘坐人数分别为2x 人 和 5x 人,再根据它们与单圈载客最大 量之间的关系列方程.
解 :设乘坐中天门索道与桃花源索道的分别为 5 x 人 和 2x 人
根据与单圈载客最大量之间的关系,得
5x—200=2x+100.
移项,得 5x—2x=100+200.
合并同类项,得 3x=300.
系数化为1,得 X=100.
所以 2x=200, 5x=500.
答:乘坐中天门索道与桃花源索道的团队分别为200人和500人.
学以致用
善总结—课堂小结
通过本节课的学习,你的收获是------
当堂测—解方程
1. 解下列方程:(6分钟)
(1)3x=4x+3; (2)6x-8=4x;
(3)6y-7=4y-5;
2 .李明出生时父亲28岁,现在父亲的年龄是李明年龄的3倍, 求现在李明的年龄.
1.完成教材习题5.2 1,5,6题;
2.实践作业:“校园读书日”期间,请同学们作为“小志愿者”通过整理图书馆的 一批书籍,算出两名同学每分钟分别可以整理多少册 小组合作,运用方程的知
识,完成问题。需要多长时间才能共同完成
任务:(1)两名“小志愿者”整理一分钟书籍
(2)两名计时员,计时1分钟,并算出“小志愿者”各自完成的书籍量。
(3)两名分配员,将需要整理的书籍平均分成两份,从其中一份中拿出100
册,放到另一份中,效率快的同学整理大份。
(4)两名设计员:将实践问题,转化成数学方程问题,并组内合作解答。
课后作业
共 勉
本单元我们从现实情境初始泰山、游历泰山出发,学习了一
元一次方程的定义、解法。
通过本单元的学习,希望同学们都有“会当凌绝顶, 一览众
山小"的志气和豪气,克服困难,在学习过程中学会“ 用数学 的眼光观察现实世界"“用数学的思维思考现实世界”,最后 能达到“会用数学的语言表达现实世界”,从而达到我们自己 学习数学的顶峰。
同课章节目录
