人教版七年级数学下册期末素养评估(第七至第十二章)课件(共49张PPT)
文档属性
| 名称 | 人教版七年级数学下册期末素养评估(第七至第十二章)课件(共49张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 21:44:11 | ||
图片预览











文档简介
(共49张PPT)
期末素养评估(第七至第十二章)
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一
项是符合题目要求的.
1.(2024·云浮罗定期中)2024年巴黎奥运会是历史上第33届夏季奥运会,于7月26日开
幕.如图是本届奥运会的吉祥物“弗里热”,将图中的“弗里热”通过平移可得到下列选
项中的( )
D
【解析】由平移的性质可知,平移不改变图形的形状和大小,平移后的图形是选项D.
2.下列调查适合全面调查的是( )
A.了解某市居民对废电池的处理情况
B.日光灯管厂要检测一批灯管的使用寿命
C.了解在校大学生的主要娱乐方式
D.调查乘坐飞机的旅客是否携带了违禁物品
【解析】A.了解某市居民对废电池的处理情况,适合抽样抽查,故不符合题意;
B.日光灯管厂要检测一批灯管的使用寿命,适合抽样抽查,故不符合题意;C.了解在校大学生的主要娱乐方式,适合抽样抽查,故不符合题意;D.调查乘坐飞机的旅客是否携带了违禁物品,适合全面调查,故符合题意.
D
C
D
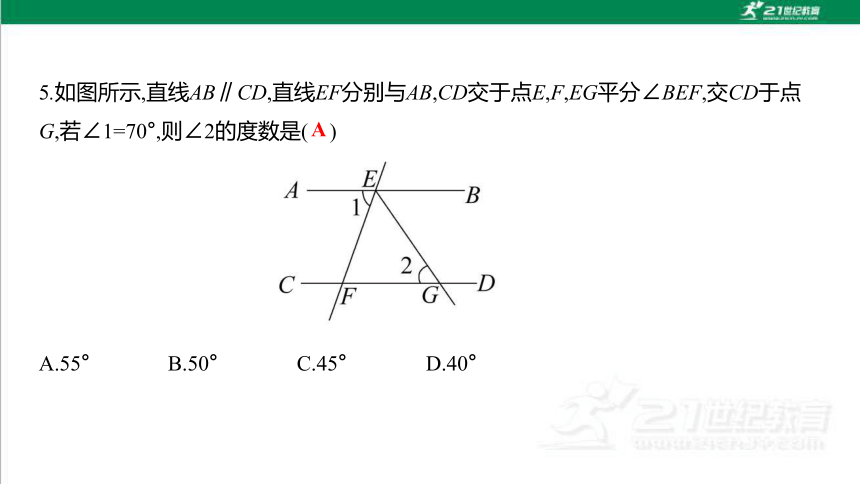
5.如图所示,直线AB∥CD,直线EF分别与AB,CD交于点E,F,EG平分∠BEF,交CD于点
G,若∠1=70°,则∠2的度数是( )
A.55° B.50° C.45° D.40°
A
6.(2024·韶关期末)下列命题属于真命题的是( )
A.同旁内角相等,两直线平行
B.平行于同一条直线的两条直线平行
C.y轴上所有点的纵坐标为0
D.所有无限小数都是无理数
【解析】A.同旁内角互补,两直线平行,故A选项错误;
B.平行于同一条直线的两条直线平行,是真命题,故B选项正确;
C.y轴上所有点的横坐标为0,故C选项错误;
D.所有无限不循环小数都是无理数,故D选项错误.
B
C
8.(2024·深圳宝安质检)若点P(x-4,2x+6)在平面直角坐标系的第二象限内,则x的取值
范围在数轴上可表示为( )
C
A
10.(2024·广州越秀期中)如图所示,在平面直角坐标系中,有若干个整数点,其顺序按
图中“ ”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0),(4,0).根据这个规律探索可得,第
2 024个点的坐标为( )
A.(64,7) B.(64,8)
C.(65,7) D.(65,8)
A
81
(0,2)或(0,-2)
13.(2024·梅州五华期末)某校连续四个月开展了学科知识模拟测试,并将测试成绩整理,绘制了如图所
示的统计图(四次参加模拟测试的学生人数不变),下列四个结论中不正确的是_______(填写序号).
①共有500名学生参加模拟测试;
②从第1个月到第4个月,测试成绩“优秀”
的学生人数在总人数中的占比逐渐增长;
③第4个月增长的“优秀”人数比第3个月
增长的“优秀”人数多;
④第4个月测试成绩“优秀”的学生人数达
到100人.
④
【解析】测试的学生人数为:10+250+150+90=500(名),故①结论正确;
由折线统计图可知,从第1个月到第4个月,测试成绩“优秀”的学生人数在总人数中的占比逐月增长,故②结论正确;
由折线统计图可知,第4个月增长的“优秀”人数比第3个月增长的“优秀”人数多,故③结论正确;
第4个月测试成绩“优秀”的学生人数为:500×17%=85(名),故④结论不正确.
∴不正确的是④.
14.如图所示,在平面直角坐标系中,点E(8,0),点F(0,8),将三角形OEF向下平移2个单位
长度得到三角形ABC,BC与x轴交于点G,CO=GO,则阴影部分的面积是_______.
14
27
18.如图所示,CD⊥AB于点D,点F是BC上任意一点,过点F作FE⊥AB于点E,且∠1=∠2.
(1)求证:DG∥BC;
(2)若∠2=35°,CD平分∠BCA,求∠3的度数.
【解析】(1)∵CD⊥AB,FE⊥AB,
∴∠CDB=∠FEB=90°,
∴FE∥CD,∴∠DCB=∠2.
∵∠1=∠2,∴∠1=∠DCB,∴DG∥BC.
(2)∵∠DCB=∠2,∠2=35°,
∴∠DCB=35°.
∵CD平分∠BCA,
∴∠ACB=2∠DCB=70°.
∵DG∥CB,
∴∠3=∠ACB=70°.
四、解答题(二):本大题共3小题,每小题9分,共27分.
19.(2024·汕头潮阳期中)这是某单位的平面示意图,已知大门的坐标为(-3,0),花坛的坐标为(0,-1).
(1)根据上述条件建立平面直角坐标系;
(2)建筑物A的坐标为(3,1),请在图中标出点A的位置;
(3)建筑物B在大门北偏东45°的方向,并且B在花坛的正北方向处,请写出点B的坐标.
【解析】(1)如图所示.
(2)点A如图所示.
(3)点B如图所示.
∴B(0,3).
20.(2024·惠州惠阳期末)为增强学生环保意识.实施垃圾分类管理.某中学举行了“垃圾分类知识竞赛“并随机抽取了部分学生的竞赛成绩绘制了如下不完整的统计图表.
根据所给信息,解答下列问题.
知识竞赛成绩频数分布表:
组别 成绩(分数) 人数
A 95≤x<100 300
B 90≤x<95 a
C 85≤x<90 150
D 80≤x<85 200
E x<80 b
(1)a=________,b=________.
(2)请求出扇形统计图中C组所在扇形的圆心角的度数.
(3)已知该中学有3 500名学生,请估算该中学学生知识竞赛成绩低于80分的人数.
∴2|2a-3|+3|2a-4|
=2(2a-3)-3(2a-4)
=4a-6-6a+12
=6-2a.
五、解答题(三):本大题共2小题,第22题13分,第23题14分,共27分.
22.(2024·深圳福田期中)根据以下素材,探索完成任务.
背景 福田区某学校拟向公交公司租借A,B两种车共8辆,用于接送八年级师生去实践基地参加社会实践活动
素
材 素材1 A型车最大载客量是50人,B型车的最大载客量是35人,已知此前明华中学租用了3辆A型车和2辆B型车花费了1 950元,安阳中学租用了4辆A型车和4辆B型车花费了
3 000元
素材2 八年级的师生共有305人,根据学校预算,租车的费用需要控制在2 900元(包含2 900元)以内
问题
解决 任务1 A型车和B型车每辆的租金分别是多少元
任务2 根据素材2中该校八年级师生的实际情况,该如何租车 请给出所有满足条件的租车方案
任务3 在所有满足条件的租车方案中,花费最少的方案比预算2 900元省多少元
选择方案2所需总租金为450×3+300×5=2 850(元).
∵2 700<2 850,2 900-2 700=200(元),
∴花费最少的是方案1,节省了200元.
23.(2024·梅州兴宁期末)综合与实践
【问题情境】在综合与实践课上,同学们以“一个含30°的直角三角尺和两条平行线”为背景开展数学活动.如图1,已知两直线a,b且a∥b和直角三角形ABC,∠BCA=90°,∠BAC=30°,∠ABC=60°.
(1)在图1中,∠1=46°,求∠2的度数;
【深入探究】
(2)如图2,创新小组的同学把直线a向上平移,并把∠2的位置改变,发现∠2-∠1=120°,请说明理由;
【拓展应用】
(3)缜密小组在创新小组发现结论的基础上,将图2中的图形继续变化得到图3,AC平分∠BAM,此时发现∠1与∠2又存在新的数量关系,请直接写出∠1与∠2的数量关系.
【解析】(1)如图所示,
∵∠ACB=90°,∠1+∠ACB+∠3=180°,
∴∠1+∠3=180°-∠ACB=90°.
∵∠1=46°,
∴∠3=90°-∠1=44°,
∵a∥b,
∴∠2=∠3=44°.
(2)如图所示,过点B作BD∥a,
则∠ABD=180°-∠2,
∵a∥b,
∴BD∥b∥a,
∴∠CBD=∠1.
∵∠ABC=60°,
∴∠ABD+∠CBD=180°-∠2+∠1=60°,
∴∠2-∠1=120°.
(3)∠1=∠2.
如图所示,过点C作CE∥a,
则∠2=∠BCE,
∵AC平分∠BAM,∴∠BAC=∠CAM=30°,
∴∠MAB=60°.
∵a∥b,∴CE∥b,
∴∠1=∠MAB=60°,∠ACE=∠MAC=30°,
∴∠BCE=90°-∠ACE=60°,
∴∠2=∠BCE=60°,
∴∠1=∠2=60°.
期末素养评估(第七至第十二章)
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一
项是符合题目要求的.
1.(2024·云浮罗定期中)2024年巴黎奥运会是历史上第33届夏季奥运会,于7月26日开
幕.如图是本届奥运会的吉祥物“弗里热”,将图中的“弗里热”通过平移可得到下列选
项中的( )
D
【解析】由平移的性质可知,平移不改变图形的形状和大小,平移后的图形是选项D.
2.下列调查适合全面调查的是( )
A.了解某市居民对废电池的处理情况
B.日光灯管厂要检测一批灯管的使用寿命
C.了解在校大学生的主要娱乐方式
D.调查乘坐飞机的旅客是否携带了违禁物品
【解析】A.了解某市居民对废电池的处理情况,适合抽样抽查,故不符合题意;
B.日光灯管厂要检测一批灯管的使用寿命,适合抽样抽查,故不符合题意;C.了解在校大学生的主要娱乐方式,适合抽样抽查,故不符合题意;D.调查乘坐飞机的旅客是否携带了违禁物品,适合全面调查,故符合题意.
D
C
D
5.如图所示,直线AB∥CD,直线EF分别与AB,CD交于点E,F,EG平分∠BEF,交CD于点
G,若∠1=70°,则∠2的度数是( )
A.55° B.50° C.45° D.40°
A
6.(2024·韶关期末)下列命题属于真命题的是( )
A.同旁内角相等,两直线平行
B.平行于同一条直线的两条直线平行
C.y轴上所有点的纵坐标为0
D.所有无限小数都是无理数
【解析】A.同旁内角互补,两直线平行,故A选项错误;
B.平行于同一条直线的两条直线平行,是真命题,故B选项正确;
C.y轴上所有点的横坐标为0,故C选项错误;
D.所有无限不循环小数都是无理数,故D选项错误.
B
C
8.(2024·深圳宝安质检)若点P(x-4,2x+6)在平面直角坐标系的第二象限内,则x的取值
范围在数轴上可表示为( )
C
A
10.(2024·广州越秀期中)如图所示,在平面直角坐标系中,有若干个整数点,其顺序按
图中“ ”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0),(4,0).根据这个规律探索可得,第
2 024个点的坐标为( )
A.(64,7) B.(64,8)
C.(65,7) D.(65,8)
A
81
(0,2)或(0,-2)
13.(2024·梅州五华期末)某校连续四个月开展了学科知识模拟测试,并将测试成绩整理,绘制了如图所
示的统计图(四次参加模拟测试的学生人数不变),下列四个结论中不正确的是_______(填写序号).
①共有500名学生参加模拟测试;
②从第1个月到第4个月,测试成绩“优秀”
的学生人数在总人数中的占比逐渐增长;
③第4个月增长的“优秀”人数比第3个月
增长的“优秀”人数多;
④第4个月测试成绩“优秀”的学生人数达
到100人.
④
【解析】测试的学生人数为:10+250+150+90=500(名),故①结论正确;
由折线统计图可知,从第1个月到第4个月,测试成绩“优秀”的学生人数在总人数中的占比逐月增长,故②结论正确;
由折线统计图可知,第4个月增长的“优秀”人数比第3个月增长的“优秀”人数多,故③结论正确;
第4个月测试成绩“优秀”的学生人数为:500×17%=85(名),故④结论不正确.
∴不正确的是④.
14.如图所示,在平面直角坐标系中,点E(8,0),点F(0,8),将三角形OEF向下平移2个单位
长度得到三角形ABC,BC与x轴交于点G,CO=GO,则阴影部分的面积是_______.
14
27
18.如图所示,CD⊥AB于点D,点F是BC上任意一点,过点F作FE⊥AB于点E,且∠1=∠2.
(1)求证:DG∥BC;
(2)若∠2=35°,CD平分∠BCA,求∠3的度数.
【解析】(1)∵CD⊥AB,FE⊥AB,
∴∠CDB=∠FEB=90°,
∴FE∥CD,∴∠DCB=∠2.
∵∠1=∠2,∴∠1=∠DCB,∴DG∥BC.
(2)∵∠DCB=∠2,∠2=35°,
∴∠DCB=35°.
∵CD平分∠BCA,
∴∠ACB=2∠DCB=70°.
∵DG∥CB,
∴∠3=∠ACB=70°.
四、解答题(二):本大题共3小题,每小题9分,共27分.
19.(2024·汕头潮阳期中)这是某单位的平面示意图,已知大门的坐标为(-3,0),花坛的坐标为(0,-1).
(1)根据上述条件建立平面直角坐标系;
(2)建筑物A的坐标为(3,1),请在图中标出点A的位置;
(3)建筑物B在大门北偏东45°的方向,并且B在花坛的正北方向处,请写出点B的坐标.
【解析】(1)如图所示.
(2)点A如图所示.
(3)点B如图所示.
∴B(0,3).
20.(2024·惠州惠阳期末)为增强学生环保意识.实施垃圾分类管理.某中学举行了“垃圾分类知识竞赛“并随机抽取了部分学生的竞赛成绩绘制了如下不完整的统计图表.
根据所给信息,解答下列问题.
知识竞赛成绩频数分布表:
组别 成绩(分数) 人数
A 95≤x<100 300
B 90≤x<95 a
C 85≤x<90 150
D 80≤x<85 200
E x<80 b
(1)a=________,b=________.
(2)请求出扇形统计图中C组所在扇形的圆心角的度数.
(3)已知该中学有3 500名学生,请估算该中学学生知识竞赛成绩低于80分的人数.
∴2|2a-3|+3|2a-4|
=2(2a-3)-3(2a-4)
=4a-6-6a+12
=6-2a.
五、解答题(三):本大题共2小题,第22题13分,第23题14分,共27分.
22.(2024·深圳福田期中)根据以下素材,探索完成任务.
背景 福田区某学校拟向公交公司租借A,B两种车共8辆,用于接送八年级师生去实践基地参加社会实践活动
素
材 素材1 A型车最大载客量是50人,B型车的最大载客量是35人,已知此前明华中学租用了3辆A型车和2辆B型车花费了1 950元,安阳中学租用了4辆A型车和4辆B型车花费了
3 000元
素材2 八年级的师生共有305人,根据学校预算,租车的费用需要控制在2 900元(包含2 900元)以内
问题
解决 任务1 A型车和B型车每辆的租金分别是多少元
任务2 根据素材2中该校八年级师生的实际情况,该如何租车 请给出所有满足条件的租车方案
任务3 在所有满足条件的租车方案中,花费最少的方案比预算2 900元省多少元
选择方案2所需总租金为450×3+300×5=2 850(元).
∵2 700<2 850,2 900-2 700=200(元),
∴花费最少的是方案1,节省了200元.
23.(2024·梅州兴宁期末)综合与实践
【问题情境】在综合与实践课上,同学们以“一个含30°的直角三角尺和两条平行线”为背景开展数学活动.如图1,已知两直线a,b且a∥b和直角三角形ABC,∠BCA=90°,∠BAC=30°,∠ABC=60°.
(1)在图1中,∠1=46°,求∠2的度数;
【深入探究】
(2)如图2,创新小组的同学把直线a向上平移,并把∠2的位置改变,发现∠2-∠1=120°,请说明理由;
【拓展应用】
(3)缜密小组在创新小组发现结论的基础上,将图2中的图形继续变化得到图3,AC平分∠BAM,此时发现∠1与∠2又存在新的数量关系,请直接写出∠1与∠2的数量关系.
【解析】(1)如图所示,
∵∠ACB=90°,∠1+∠ACB+∠3=180°,
∴∠1+∠3=180°-∠ACB=90°.
∵∠1=46°,
∴∠3=90°-∠1=44°,
∵a∥b,
∴∠2=∠3=44°.
(2)如图所示,过点B作BD∥a,
则∠ABD=180°-∠2,
∵a∥b,
∴BD∥b∥a,
∴∠CBD=∠1.
∵∠ABC=60°,
∴∠ABD+∠CBD=180°-∠2+∠1=60°,
∴∠2-∠1=120°.
(3)∠1=∠2.
如图所示,过点C作CE∥a,
则∠2=∠BCE,
∵AC平分∠BAM,∴∠BAC=∠CAM=30°,
∴∠MAB=60°.
∵a∥b,∴CE∥b,
∴∠1=∠MAB=60°,∠ACE=∠MAC=30°,
∴∠BCE=90°-∠ACE=60°,
∴∠2=∠BCE=60°,
∴∠1=∠2=60°.
同课章节目录
