全册综合试题-- 高中数学人教A版(2019)选择性必修第三册(A卷)(含解析)
文档属性
| 名称 | 全册综合试题-- 高中数学人教A版(2019)选择性必修第三册(A卷)(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-03 08:46:58 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
全册综合试题-- 高中数学人教A版(2019)选择性必修第三册(A卷)
本试卷满分150分,考试时间120分钟。
注意事项:
1.答题前,务必将自己的姓名、班级、考号填写在答题卡规定的位置上。
答选择题时,必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦
2.擦干净后,再选涂其它答案标号。
3.答非选择题时,必须使用0.5毫米黑色签字笔,将答案书写在答题卡规定的位置上。
4.所有题目必须在答题卡上作答,在试题卷上答题无效。
一、单项选择题:本大题共 8 小题,每小题 5 分,共 40 分. 在每小题给出的四个选项中,只有一个选项是正确的.请把正确的选项填涂在答题卡相应的位置上.
1.色差和色度是衡量毛绒玩具质量优劣的重要指标,现抽检一批产品测得数据列于表中:已知该产品的色度y和色差x之间满足线性相关关系,且,现有一对测量数据为,则该数据的残差为( )
色差x 21 23 25 27
色度y 15 18 19 20
A.-0.96 B.-0.8 C.0.8 D.0.96
2.现安排甲、乙、丙、丁、戊5名同学参加2024年杭州亚运会志愿者服务活动,有翻译、导游、礼仪、司机四项工作可以安排,以下说法正确的是( )
A.每人都安排一项工作的不同方法数为
B.每人都安排一项工作,每项工作至少有一人参加,则不同的方法数为
C.如果司机工作不安排,其余三项工作至少安排一人,则这5名同学全部被安排的不同方法数为
D.每人都安排一项工作,每项工作至少有一人参加,甲、乙不会开车但能从事其他三项工作,丙、丁、戊都能胜任四项工作,则不同安排方案的种数是
3.对任意的实数x,若,则的值为( )
A.15 B.6 C.1 D.20
4.甲、乙两队进行乒乓球比赛,比赛采取五局三胜制(当一队赢得三场胜利时,该队获胜,比赛结束),假设每局比赛甲队胜乙队的概率均为p,没有平局,且各局比赛相互独立,则甲队以获胜的概率可以表示为( )
A. B.
C. D.
5.某校A,B,C,D,E五名学生分别上台演讲,若A须在B前面出场,则不同的出场次序有( )
A.18种 B.36种 C.60种 D.72种
6.数学活动小组由12名同学组成,现将12名同学平均分成四组分别研究四个不同课题,且每组只研究一个课题,并要求每组选出一名组长,则不同的分配方案的种数为( )
A. B. C. D.
7.从1,2,3,4,5,6,7,8,9中不放回地依次取2个数,事件A为“第一次取到的是奇数”,B为“第二次取到的是3的整数倍”,则( )
A. B. C. D.
8.设,随机变量的分布列分别如下,则( )
0 1 2
P
0 1 2
P
A.若,则 B.若,则
C.若,则 D.若,则
二、多项选择题:本大题共 3 小题,每小题 6 分,共 18 分. 在每小题给出的四个选项中,有多项符合题目要求. 全部选对得 6 分,选对但不全的得部分分,有选错的得0分.
9.某校篮球社团准备招收新成员,要求通过考核才能加入,考核规则如下:报名参加该社团的学生投篮n次,若投中次数不低于投篮次数的,则通过考核.学生甲准备参加该社团,且他的投篮命中率为0.9,每次是否投中相互独立.若,记甲通过考核的概率为,若,记甲通过考核的概率为,若,记甲通过考核的概率为,若,记甲通过考核的概率为,若,记甲通过考核的概率为,则( )
A. B. C. D.
10.某个国家某种病毒传播的中期,感染人数y和时间x(单位:天)在18天里的散点图如图所示,下面四个回归方程类型中有可能适宜作为感染人数y和时间x的回归方程类型的是( )
A. B. C. D.
11.某校文艺汇演共6个节目,其中歌唱类节目3个,舞蹈类节目2个,语言类节目1个,则下列说法正确的是( )
A.若以歌唱类节目开场,则有360种不同的出场顺序
B.若舞蹈类节目相邻,则有120种出场顺序
C.若舞蹈类节目不相邻,则有240种不同的出场顺序
D.从中挑选2个不同类型的节目参加市艺术节,则有11种不同的选法
三、填空题:本大题共 3 小题,每小题 5 分,共 15 分.
12.某校决定从高一、高二两个年级分别抽取100人、60人参加演出活动,高一100人中女生占,高二60人中女生占,则从中抽取1人恰好是女生的概率为________.
13.设一个四位数的个位数、十位数、百位数、千位数分别为a,b,c,d,当时,称这个四位数为“和对称四位数”,且为这个“和对称四位数”的对称和,例如8440是一个“和对称四位数”,其对称和为8,则对称和不大于4的“和对称四位数”的个数为_______________.
14.已知随机变量,且,若,则的最小值为________.
四、解答题:本题共 5 小题,共 77 分. 解答应写出文字说明、证明过程或演算步骤.
15.随着经济的发展,富裕起来的人们健康意识日益提升,越来越多的人走向公园 场馆,投入健身运动中,成为一道美丽的运动风景线.某兴趣小组为了解本市不同年龄段的市民每周锻炼时长情况,随机抽取400人进行调查,得到如下表的统计数据:
周平均锻炼时间少于5小时 周平均锻炼时间不少于5小时 合计
50岁以下 80 120 200
50岁以上(含50) 50 150 200
合计 130 270 400
(1)根据表中数据,依据的独立性检验,能否认为周平均锻炼时长与年龄有关联?
(2)现从50岁以上(含50)的样本中按周平均锻炼时间是否少于5小时,用分层随机抽样法抽取8人做进一步访谈,再从这8人中随机抽取3人填写调查问卷.记抽取3人中周平均锻炼时间不少于5小时的人数为X,求X的分布列和数学期望.
参考公式及数据:,其中.
0.025 0.01 0.005 0.001
5.024 6.635 7.879 10.828
16.某种产品的加工需要经过5道工序.
(1)如果其中某道工序不能放在最后,那么有多少种加工顺序?
(2)如果其中某2道工序既不能放在最前,也不能放在最后,那么有多少种加工顺序?
(3)如果其中某2道工序必须相邻,那么有多少种加工顺序?
(4)如果其中某2道工序不能相邻,那么有多少种加工顺序?
17.有不同的红球8个,不同的白球7个:
(1)从中取出1个球,共有多少种不同的取法?
(2)从中取出2个颜色不同的球,共有多少种不同的取法?
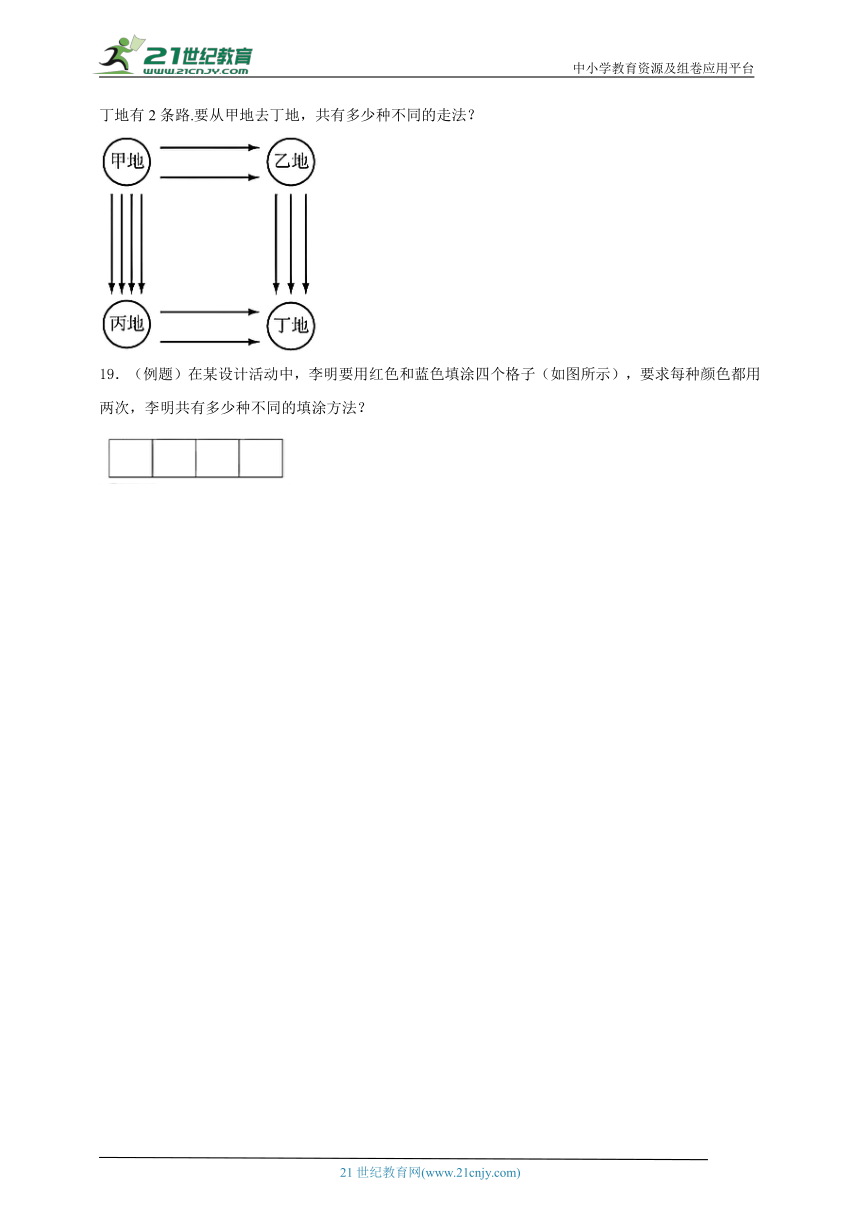
18.如图所示,从甲地到乙地有2条路,从乙地到丁地有3条路;从甲地到丙地有4条路,从丙地到丁地有2条路.要从甲地去丁地,共有多少种不同的走法?
19.(例题)在某设计活动中,李明要用红色和蓝色填涂四个格子(如图所示),要求每种颜色都用两次,李明共有多少种不同的填涂方法?
参考答案
1.答案:C
解析:由题意可知,,
,
将代入,
即,解得,
所以,
当时,,
所以该数据的残差为.
故选:C.
2.答案:D
解析:①每人都安排一项工作的不同方法数为,即选项A错误,
②每项工作至少有一人参加,则不同的方法数为,即选项B错误,
③如果司机工作不安排,其余三项工作至少安排一人,
则这5名同学全部被安排的不同方法数为:
(),即选项C错误,
④分两种情况:第一种,安排一人当司机,
从丙、丁、戊选一人当司机有,
从余下四人中安排三个岗位,
故有;
第二种情况,安排两人当司机,从丙、丁、戊选两人当司机有,
从余下三人中安排三个岗位,故有;
所以每项工作至少有一人参加,
甲、乙不会开车但能从事其他三项工作,丙、丁、戊都能胜任四项工作,
则不同安排方案的种数是,
即选项D正确,
故选:D.
3.答案:C
解析:因为,
令,可得.
故选:C.
4.答案:C
解析:甲队以获胜,则两队共比赛了4局,且第4局一定是甲获胜,前3局里甲获胜了2局,故概率为,即.
故选:C.
5.答案:C
解析:因为A,B,C,D,E五名学生分别上台演讲,且A须在B前面出场,
所以有种出场顺序.
故选:C
6.答案:A
解析:将这12名同学平均分成四组分别研究四个不同课题,且每组只研究一个课题,只需每个课题依次选三个人即可,共有中选法,最后选一名组长各有3种,故不同的分配方案为:,
故选A.
7.答案:B
解析:由题意
事件为“第一次取到的是奇数且第二次取到的是3的整数倍”:若第一次取到的为3或9,
第二次有2种情况;若第一次取到的为1,5,7,第二次有3种情况,故共有个事件
由条件概率的定义:,
故选:B.
8.答案:A
解析:设随机变量为X,其可能的取值是,对应概率为,
则其数学期望(均值)为,
其方差为:
,
则,,
;
,,
;
,
若,则,,故,即,故A正确,B错误;
若,则,但无法判断与1的大小,故无法判断,的大小,故CD错误.
故选:A.
9.答案:AD
解析:记甲的投中次数为X,则.
对于A选项,当时,甲通过考核最少要投中2次,
0.972,A正确.
对于B选项,当时,将甲的投中次数分为以下3种情况,
分别为,,..
当时,甲通过考核最少要投中11次.若前20次里投中次数不少于11,
则第21次不管投中与否都通过考核;
若前20次投中10次,则第21次投中才能通过考核;
若前20次里投中次数不超过9,则第21次不管投中与否都不能通过考核.
,显然,B错误.
对于C选项,当时,将甲的投中次数分为以下3种情况,
分别为,,..
当时,若前19次里投中次数不少于10,
则第20次不管投中与否都通过考核;
若前19次投中9次,则第20次投中才能通过考核;
若前19次里投中次数不超过8,则第20次不管投中与否都不能通过考核.
,显然,C错误.
对于D选项,当时,将甲的投中次数分为以下4种情况,
分别为,,,..
当时,甲通过考核最少要投中11次.若前20次里投中次数不少于11,
则第21,22次不管投中与否都通过考核;
若前20次投中10次,则第21,22次至少要投中1次才能通过考核;
若前20次投中9次,则第21,22次都投中才能通过考核;
若前20次里投中次数不超过8,则第21,22次不管投中与否都不能通过考核.
,
.
,
所以,,,D正确.
故选:AD
10.答案:BD
解析:根据图象可知,函数图象随着自变量的变大,函数值增长速度越来越快,结合选项,可判定为指数函数或的特征,
故选:BD.
11.答案:AD
解析:A:从3个歌唱节目选1个作为开场,
有种方法,后面的5个节目全排列,
所以符合题意的方法共有种,故A正确;
B:将2个舞蹈节目捆绑在一起,有种方法,
再与其余4个节目全排列,
所以符合题意的方法共有,故B错误;
C:除了2个舞蹈节目以外的4个节目全排列,
有种,再由4个节目组成的5个空插入2个舞蹈节目,
所以符合题意的方法有种,故C错误;
D:符合题意的情况可能是1个歌唱1个舞蹈、
1个歌唱1个语言、1个舞蹈1个语言,
所以不同的选法共种,故D正确.
故选:AD.
12.答案:
解析:用A,分别表示取的一人是来自高一和高二,B表示抽取一个恰好是女生,则由已知可知:,,
且,,
所以
故答案为:
13.答案:40
解析:设.
当时:
d的可能值为1(对应),共1种组合.
的解有2种:,.
四位数的个数:;
当时:
d的可能值为1, 2(对应),共 2种组合.
的解有 3 种:,,.
四位数的个数:;
当时:
d的可能值为1, 2, 3(对应),共3种组合.
的解有4种:,,,.
四位数的个数:;
当 时:
d的可能值为1, 2, 3, 4(对应),共 4 种组合.
的解有5种:,,,,.
四位数的个数:.
将以上结果相加,总数为 .
因此,对称和不大于4的“和对称四位数”共有40个.
故答案为:40.
14.答案:
解析:,可得正态分布曲线的对称轴为,
又,,即.
则,
当且仅当,即时,等号成立.
故答案为:.
15.答案:(1)能
(2)分布列见解析,
解析:(1)零假设周平均锻炼时长与年龄无关联.
由列联表中的数据,可得,
根据小概率值的独立性检验,我们推断不成立,
即认为周平均锻炼时长与年龄有关联,此推断犯错误的概率不大于0.01.
(2)抽取的8人中,周平均锻炼时长少于5小时的有人,不少于5小时的有人,
则X所有可能的取值为1,2,3,
所以;;,
所以随机变量X的分布列为:
X 1 2 3
P
所以数学期望.
16.答案:(1)96
(2)36
(3)48
(4)72
解析:(1)先从另外4道工序中任选1道工序放在最后,有种不同的排法,再将剩余的4道工序全排列,有种不同的排法,故由分步乘法原理可得,共有种加工顺序;
(2)先从另外3道工序中任选2道工序放在最前和最后,有种不同的排法,再将剩余的3道工序全排列,有种不同的排法,故由分步乘法原理可得,共有种加工顺序;
(3)先排这2道工序,有种不同的排法,再将它们看做一个整体,与剩余的工序全排列,有种不同的排法,故由分步乘法原理可得,共有种加工顺序;
(4)先排其余的3道工序,有种不同的排法,出现4个空位,再将这2道工序插空,有种不同的排法,所以由分步乘法原理可得,共有种加工顺序,
17.答案:(1)15
(2)56
解析:(1).
(2).
18.答案:14种
解析:从甲地到丁地有两类方法.
第一类:从甲地经过乙地到达丁地,共有种不同方法;
第二类:从甲地经过丙地到达丁地,共有种不同方法.
所以从甲地到丁地共有种不同的方法.
19.答案:6种
解析:用R表示红色,用B表示蓝色,例如,RBRB表示第一个和第三个格子涂红色,第二个和第四个格子涂蓝色,
因为红色和蓝色都要用两次,为了简化问题,考虑涂红色的格子是否相邻,则填涂结果可以分为两类:涂红色的格子相邻,涂红色的格子不相邻.
涂红色的格子相邻的方法有:RRBB,BRRB,BBRR,共3种;
涂红色的格子不相邻的方法有:RBRB,BRBR,RBBR,共3种.
依据分类加法计数原理,李明共有种不同的涂法.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
全册综合试题-- 高中数学人教A版(2019)选择性必修第三册(A卷)
本试卷满分150分,考试时间120分钟。
注意事项:
1.答题前,务必将自己的姓名、班级、考号填写在答题卡规定的位置上。
答选择题时,必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦
2.擦干净后,再选涂其它答案标号。
3.答非选择题时,必须使用0.5毫米黑色签字笔,将答案书写在答题卡规定的位置上。
4.所有题目必须在答题卡上作答,在试题卷上答题无效。
一、单项选择题:本大题共 8 小题,每小题 5 分,共 40 分. 在每小题给出的四个选项中,只有一个选项是正确的.请把正确的选项填涂在答题卡相应的位置上.
1.色差和色度是衡量毛绒玩具质量优劣的重要指标,现抽检一批产品测得数据列于表中:已知该产品的色度y和色差x之间满足线性相关关系,且,现有一对测量数据为,则该数据的残差为( )
色差x 21 23 25 27
色度y 15 18 19 20
A.-0.96 B.-0.8 C.0.8 D.0.96
2.现安排甲、乙、丙、丁、戊5名同学参加2024年杭州亚运会志愿者服务活动,有翻译、导游、礼仪、司机四项工作可以安排,以下说法正确的是( )
A.每人都安排一项工作的不同方法数为
B.每人都安排一项工作,每项工作至少有一人参加,则不同的方法数为
C.如果司机工作不安排,其余三项工作至少安排一人,则这5名同学全部被安排的不同方法数为
D.每人都安排一项工作,每项工作至少有一人参加,甲、乙不会开车但能从事其他三项工作,丙、丁、戊都能胜任四项工作,则不同安排方案的种数是
3.对任意的实数x,若,则的值为( )
A.15 B.6 C.1 D.20
4.甲、乙两队进行乒乓球比赛,比赛采取五局三胜制(当一队赢得三场胜利时,该队获胜,比赛结束),假设每局比赛甲队胜乙队的概率均为p,没有平局,且各局比赛相互独立,则甲队以获胜的概率可以表示为( )
A. B.
C. D.
5.某校A,B,C,D,E五名学生分别上台演讲,若A须在B前面出场,则不同的出场次序有( )
A.18种 B.36种 C.60种 D.72种
6.数学活动小组由12名同学组成,现将12名同学平均分成四组分别研究四个不同课题,且每组只研究一个课题,并要求每组选出一名组长,则不同的分配方案的种数为( )
A. B. C. D.
7.从1,2,3,4,5,6,7,8,9中不放回地依次取2个数,事件A为“第一次取到的是奇数”,B为“第二次取到的是3的整数倍”,则( )
A. B. C. D.
8.设,随机变量的分布列分别如下,则( )
0 1 2
P
0 1 2
P
A.若,则 B.若,则
C.若,则 D.若,则
二、多项选择题:本大题共 3 小题,每小题 6 分,共 18 分. 在每小题给出的四个选项中,有多项符合题目要求. 全部选对得 6 分,选对但不全的得部分分,有选错的得0分.
9.某校篮球社团准备招收新成员,要求通过考核才能加入,考核规则如下:报名参加该社团的学生投篮n次,若投中次数不低于投篮次数的,则通过考核.学生甲准备参加该社团,且他的投篮命中率为0.9,每次是否投中相互独立.若,记甲通过考核的概率为,若,记甲通过考核的概率为,若,记甲通过考核的概率为,若,记甲通过考核的概率为,若,记甲通过考核的概率为,则( )
A. B. C. D.
10.某个国家某种病毒传播的中期,感染人数y和时间x(单位:天)在18天里的散点图如图所示,下面四个回归方程类型中有可能适宜作为感染人数y和时间x的回归方程类型的是( )
A. B. C. D.
11.某校文艺汇演共6个节目,其中歌唱类节目3个,舞蹈类节目2个,语言类节目1个,则下列说法正确的是( )
A.若以歌唱类节目开场,则有360种不同的出场顺序
B.若舞蹈类节目相邻,则有120种出场顺序
C.若舞蹈类节目不相邻,则有240种不同的出场顺序
D.从中挑选2个不同类型的节目参加市艺术节,则有11种不同的选法
三、填空题:本大题共 3 小题,每小题 5 分,共 15 分.
12.某校决定从高一、高二两个年级分别抽取100人、60人参加演出活动,高一100人中女生占,高二60人中女生占,则从中抽取1人恰好是女生的概率为________.
13.设一个四位数的个位数、十位数、百位数、千位数分别为a,b,c,d,当时,称这个四位数为“和对称四位数”,且为这个“和对称四位数”的对称和,例如8440是一个“和对称四位数”,其对称和为8,则对称和不大于4的“和对称四位数”的个数为_______________.
14.已知随机变量,且,若,则的最小值为________.
四、解答题:本题共 5 小题,共 77 分. 解答应写出文字说明、证明过程或演算步骤.
15.随着经济的发展,富裕起来的人们健康意识日益提升,越来越多的人走向公园 场馆,投入健身运动中,成为一道美丽的运动风景线.某兴趣小组为了解本市不同年龄段的市民每周锻炼时长情况,随机抽取400人进行调查,得到如下表的统计数据:
周平均锻炼时间少于5小时 周平均锻炼时间不少于5小时 合计
50岁以下 80 120 200
50岁以上(含50) 50 150 200
合计 130 270 400
(1)根据表中数据,依据的独立性检验,能否认为周平均锻炼时长与年龄有关联?
(2)现从50岁以上(含50)的样本中按周平均锻炼时间是否少于5小时,用分层随机抽样法抽取8人做进一步访谈,再从这8人中随机抽取3人填写调查问卷.记抽取3人中周平均锻炼时间不少于5小时的人数为X,求X的分布列和数学期望.
参考公式及数据:,其中.
0.025 0.01 0.005 0.001
5.024 6.635 7.879 10.828
16.某种产品的加工需要经过5道工序.
(1)如果其中某道工序不能放在最后,那么有多少种加工顺序?
(2)如果其中某2道工序既不能放在最前,也不能放在最后,那么有多少种加工顺序?
(3)如果其中某2道工序必须相邻,那么有多少种加工顺序?
(4)如果其中某2道工序不能相邻,那么有多少种加工顺序?
17.有不同的红球8个,不同的白球7个:
(1)从中取出1个球,共有多少种不同的取法?
(2)从中取出2个颜色不同的球,共有多少种不同的取法?
18.如图所示,从甲地到乙地有2条路,从乙地到丁地有3条路;从甲地到丙地有4条路,从丙地到丁地有2条路.要从甲地去丁地,共有多少种不同的走法?
19.(例题)在某设计活动中,李明要用红色和蓝色填涂四个格子(如图所示),要求每种颜色都用两次,李明共有多少种不同的填涂方法?
参考答案
1.答案:C
解析:由题意可知,,
,
将代入,
即,解得,
所以,
当时,,
所以该数据的残差为.
故选:C.
2.答案:D
解析:①每人都安排一项工作的不同方法数为,即选项A错误,
②每项工作至少有一人参加,则不同的方法数为,即选项B错误,
③如果司机工作不安排,其余三项工作至少安排一人,
则这5名同学全部被安排的不同方法数为:
(),即选项C错误,
④分两种情况:第一种,安排一人当司机,
从丙、丁、戊选一人当司机有,
从余下四人中安排三个岗位,
故有;
第二种情况,安排两人当司机,从丙、丁、戊选两人当司机有,
从余下三人中安排三个岗位,故有;
所以每项工作至少有一人参加,
甲、乙不会开车但能从事其他三项工作,丙、丁、戊都能胜任四项工作,
则不同安排方案的种数是,
即选项D正确,
故选:D.
3.答案:C
解析:因为,
令,可得.
故选:C.
4.答案:C
解析:甲队以获胜,则两队共比赛了4局,且第4局一定是甲获胜,前3局里甲获胜了2局,故概率为,即.
故选:C.
5.答案:C
解析:因为A,B,C,D,E五名学生分别上台演讲,且A须在B前面出场,
所以有种出场顺序.
故选:C
6.答案:A
解析:将这12名同学平均分成四组分别研究四个不同课题,且每组只研究一个课题,只需每个课题依次选三个人即可,共有中选法,最后选一名组长各有3种,故不同的分配方案为:,
故选A.
7.答案:B
解析:由题意
事件为“第一次取到的是奇数且第二次取到的是3的整数倍”:若第一次取到的为3或9,
第二次有2种情况;若第一次取到的为1,5,7,第二次有3种情况,故共有个事件
由条件概率的定义:,
故选:B.
8.答案:A
解析:设随机变量为X,其可能的取值是,对应概率为,
则其数学期望(均值)为,
其方差为:
,
则,,
;
,,
;
,
若,则,,故,即,故A正确,B错误;
若,则,但无法判断与1的大小,故无法判断,的大小,故CD错误.
故选:A.
9.答案:AD
解析:记甲的投中次数为X,则.
对于A选项,当时,甲通过考核最少要投中2次,
0.972,A正确.
对于B选项,当时,将甲的投中次数分为以下3种情况,
分别为,,..
当时,甲通过考核最少要投中11次.若前20次里投中次数不少于11,
则第21次不管投中与否都通过考核;
若前20次投中10次,则第21次投中才能通过考核;
若前20次里投中次数不超过9,则第21次不管投中与否都不能通过考核.
,显然,B错误.
对于C选项,当时,将甲的投中次数分为以下3种情况,
分别为,,..
当时,若前19次里投中次数不少于10,
则第20次不管投中与否都通过考核;
若前19次投中9次,则第20次投中才能通过考核;
若前19次里投中次数不超过8,则第20次不管投中与否都不能通过考核.
,显然,C错误.
对于D选项,当时,将甲的投中次数分为以下4种情况,
分别为,,,..
当时,甲通过考核最少要投中11次.若前20次里投中次数不少于11,
则第21,22次不管投中与否都通过考核;
若前20次投中10次,则第21,22次至少要投中1次才能通过考核;
若前20次投中9次,则第21,22次都投中才能通过考核;
若前20次里投中次数不超过8,则第21,22次不管投中与否都不能通过考核.
,
.
,
所以,,,D正确.
故选:AD
10.答案:BD
解析:根据图象可知,函数图象随着自变量的变大,函数值增长速度越来越快,结合选项,可判定为指数函数或的特征,
故选:BD.
11.答案:AD
解析:A:从3个歌唱节目选1个作为开场,
有种方法,后面的5个节目全排列,
所以符合题意的方法共有种,故A正确;
B:将2个舞蹈节目捆绑在一起,有种方法,
再与其余4个节目全排列,
所以符合题意的方法共有,故B错误;
C:除了2个舞蹈节目以外的4个节目全排列,
有种,再由4个节目组成的5个空插入2个舞蹈节目,
所以符合题意的方法有种,故C错误;
D:符合题意的情况可能是1个歌唱1个舞蹈、
1个歌唱1个语言、1个舞蹈1个语言,
所以不同的选法共种,故D正确.
故选:AD.
12.答案:
解析:用A,分别表示取的一人是来自高一和高二,B表示抽取一个恰好是女生,则由已知可知:,,
且,,
所以
故答案为:
13.答案:40
解析:设.
当时:
d的可能值为1(对应),共1种组合.
的解有2种:,.
四位数的个数:;
当时:
d的可能值为1, 2(对应),共 2种组合.
的解有 3 种:,,.
四位数的个数:;
当时:
d的可能值为1, 2, 3(对应),共3种组合.
的解有4种:,,,.
四位数的个数:;
当 时:
d的可能值为1, 2, 3, 4(对应),共 4 种组合.
的解有5种:,,,,.
四位数的个数:.
将以上结果相加,总数为 .
因此,对称和不大于4的“和对称四位数”共有40个.
故答案为:40.
14.答案:
解析:,可得正态分布曲线的对称轴为,
又,,即.
则,
当且仅当,即时,等号成立.
故答案为:.
15.答案:(1)能
(2)分布列见解析,
解析:(1)零假设周平均锻炼时长与年龄无关联.
由列联表中的数据,可得,
根据小概率值的独立性检验,我们推断不成立,
即认为周平均锻炼时长与年龄有关联,此推断犯错误的概率不大于0.01.
(2)抽取的8人中,周平均锻炼时长少于5小时的有人,不少于5小时的有人,
则X所有可能的取值为1,2,3,
所以;;,
所以随机变量X的分布列为:
X 1 2 3
P
所以数学期望.
16.答案:(1)96
(2)36
(3)48
(4)72
解析:(1)先从另外4道工序中任选1道工序放在最后,有种不同的排法,再将剩余的4道工序全排列,有种不同的排法,故由分步乘法原理可得,共有种加工顺序;
(2)先从另外3道工序中任选2道工序放在最前和最后,有种不同的排法,再将剩余的3道工序全排列,有种不同的排法,故由分步乘法原理可得,共有种加工顺序;
(3)先排这2道工序,有种不同的排法,再将它们看做一个整体,与剩余的工序全排列,有种不同的排法,故由分步乘法原理可得,共有种加工顺序;
(4)先排其余的3道工序,有种不同的排法,出现4个空位,再将这2道工序插空,有种不同的排法,所以由分步乘法原理可得,共有种加工顺序,
17.答案:(1)15
(2)56
解析:(1).
(2).
18.答案:14种
解析:从甲地到丁地有两类方法.
第一类:从甲地经过乙地到达丁地,共有种不同方法;
第二类:从甲地经过丙地到达丁地,共有种不同方法.
所以从甲地到丁地共有种不同的方法.
19.答案:6种
解析:用R表示红色,用B表示蓝色,例如,RBRB表示第一个和第三个格子涂红色,第二个和第四个格子涂蓝色,
因为红色和蓝色都要用两次,为了简化问题,考虑涂红色的格子是否相邻,则填涂结果可以分为两类:涂红色的格子相邻,涂红色的格子不相邻.
涂红色的格子相邻的方法有:RRBB,BRRB,BBRR,共3种;
涂红色的格子不相邻的方法有:RBRB,BRBR,RBBR,共3种.
依据分类加法计数原理,李明共有种不同的涂法.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
