7.3一元一次不等式组同步练习(含解析)
文档属性
| 名称 | 7.3一元一次不等式组同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 684.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
7.3一元一次不等式组
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知不等式组的解集是,则关于的方程的解为( )
A. B. C. D.
2.不等式组的解集在数轴上的表示如图所示,则符合该解集的不等式组为( )
A. B. C. D.
3.不等式组的整数解有( )
A.1个 B.2个 C.3个 D.4个
4.不等式组的解集是( )
A. B. C. D.
5.不等式组的解集为( )
A. B. C. D.
6.把一些笔记本分给几个学生,如果每人分4本,那么余9本;如果前面的每个学生分6本,那么最后一人能分到但分不到3本,因此共有学生( )
A.5人 B.6人 C.7人 D.6人或7人
7.下列各式是一元一次不等式组的是( )
A. B. C. D.
8.不等式组的解集在数轴上表示为( )
A. B.
C. D.
9.下列不等式组中,属于一元一次不等式组的是( )
A. B.
C. D.
10.不等式组的解集在数轴上表示如图,则式子的值为( )
A. B.0 C.4 D.6
11.不等式组的整数解的和为( )
A. B. C.1 D.3
12.不等式组的负整数解是( )
A. B. C. D.
二、填空题
13.下列不等式组中,是一元一次不等式组的有 .(填序号)
① ② ③ ④ ⑤
14.把一些书分给几名同学,如果每人分5本,那么余6本;如果前面的每名同学分7本,那么最后一人可分到书但不足3本.这些书共有 本.
15.请直接写出下列不等式组的解集:
(1)的解集为 ;
(2)的解集为 ;
(3)的解集为 .
16.若关于x的不等式组有解,则m的取值范围是 .
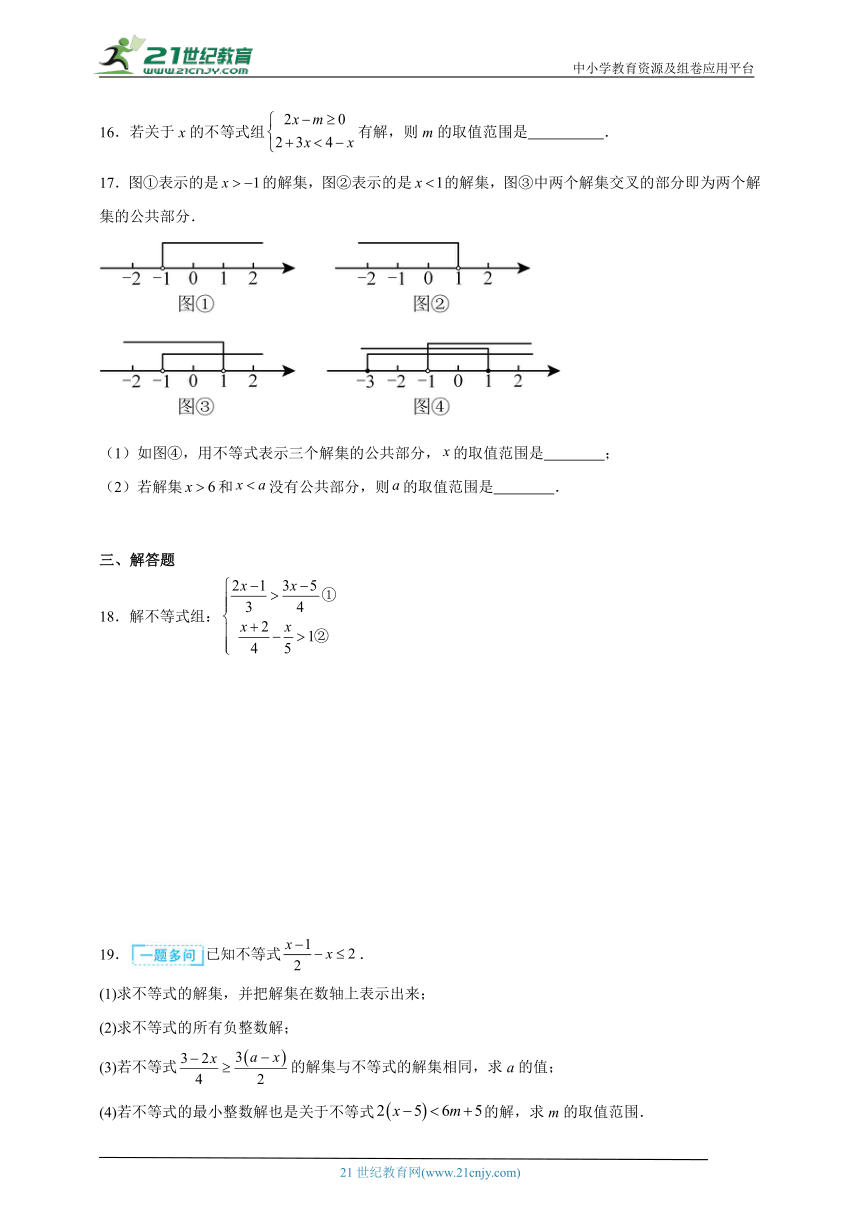
17.图①表示的是的解集,图②表示的是的解集,图③中两个解集交叉的部分即为两个解集的公共部分.
(1)如图④,用不等式表示三个解集的公共部分,的取值范围是 ;
(2)若解集和没有公共部分,则的取值范围是 .
三、解答题
18.解不等式组:
19.已知不等式.
(1)求不等式的解集,并把解集在数轴上表示出来;
(2)求不等式的所有负整数解;
(3)若不等式的解集与不等式的解集相同,求a的值;
(4)若不等式的最小整数解也是关于不等式的解,求m的取值范围.
20.解不等式组,并写出它的非负整数解.
21.已知关于x的不等式组的解集为,求的值.
22.解不等式组:.
23.解不等式组
24.解不等式组并将解集表示在数轴上.
《7.3一元一次不等式组》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D B D B B C C C B A
题号 11 12
答案 D C
1.D
【分析】此题考查解一元一次方程,解一元一次不等式组.解题关键在于掌握其方法步骤.
解不等式组,根据其解集得出关于a、b的方程,解之求得a、b的值,再还原方程,解方程即可.
【详解】解:,
解不等式①,得;
解不等式②,得.
∵不等式组的解集是,
∴.
∴,.
∴.
∴方程为.
解得.
故选:D.
2.B
【分析】本题考查的是在数轴上表示不等式的解集以及解一元一次不等式组,先根据在数轴上表示不等式解集的方法得出该不等式组的解集,再找出符合条件的不等式组即可.
【详解】解:由数轴上表示不等式解集的方法可知,该不等式组的解集为:,
A、的解集是:,故本选项不合题意;
B、的解集是:,故本选项符合题意;
C、无解,故本选项不合题意;
D、的解集是:,故本选项不合题意.
故选:B.
3.D
【分析】本题主要考查了求不等式组的整数解,先求出每个不等式的解集,再根据夹逼原则求出不等式组的解集,进而求出不等式组的整数解个数即可.
【详解】解:解不等式组
解①式得:,
解②式得:
∴不等式组的解集为,
∴共有、0、1四个整数解.
故选:D.
4.B
【分析】本题主要考查解一元一次不等式组,首先分别解出两个不等式的解集,再根据不等式组的解集确定规律找出不等式组的解集.
【详解】解:
解不等式①得,;
解不等式②得,;
所以,不等式组的解集为:.
故选:B.
5.B
【分析】本题考查了解一元一次不等式组,解题的关键是掌握解一元一次不等式组的方法.
分别求得不等式组中每个不等式的解集,再找到两个不等式解集的公共部分即为不等式组的解集.
【详解】解:
解不等式①,得.
解不等式②,得,
∴不等式组的解集为.
故选:B.
6.C
【分析】本题考查不等式组的实际应用,设共有学生人,根据每个学生分6本,那么最后一人能分到但分不到3本,列出不等式组,求出正整数解,即可.
【详解】解:设共有学生人,由题意,得:
,
解得:,
∵人数为正整数,
∴;
故选C.
7.C
【分析】本题考查了一元一次不等式组的定义:几个含有同一个未知数的一元一次不等式组合在一起,就组成了一个一元一次不等式组,熟练掌握一元一次不等式组的定义是解题的关键.
根据一元一次不等式组的定义逐项判断即可
【详解】解:A、不是一元一次不等式组,故该选项不符合题意;
B、不是一元一次不等式组,故该选项不符合题意;
C、 是一元一次不等式组,故该选项符合题意;
D、 不是一元一次不等式组,故该选项不符合题意;
故选:C
8.C
【分析】分别求出不等式组中两不等式的解集,找出两解集的公共部分,可得不等式组的解集,再在数轴上表示出来,即可得解.
本题考查的是解一元一次不等式组,正确求出每一个不等式的解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
【详解】解:
由①得,
由②得,
∴不等式组的解集为,
将解集表示在数轴上为:
.
故选:C
9.B
【分析】本题考查了一元一次不等式组.解题的关键是掌握一元一次不等式组的定义.
一元一次不等式组中指含有一个相同的未知数,并且所含未知数的项的最高次数是1次,不等式的两边都是整式,根据以上内容判断即可.
【详解】解:A、该不等式组中含有两个未知数,不是一元一次不等式组,故本选项不符合题意;
B、该不等式组是一元一次不等式组,故本选项符合题意;
C、该不等式组中的第二个不等式是分式不等式,则它不是一元一次不等式组,故本选项不符合题意;
D、该不等式组中未知数的最高次数是2,不是一元一次不等式组,故本选项不符合题意;
故选:B.
10.A
【分析】本题主要考查了解一元一次不等式组,在数轴上表示不等式组的解集,正确根据数轴上表示的解集求出a、b的值是解题的关键.分别解两个不等式求出其对应的解集,再根据数轴表示的解集,求出a、b的值即可得到答案.
【详解】解:
解不等式①得,
解不等式②得:,
根据数轴表示的解集可知不等式组的解集为,
∴,
∴,
∴,
故选A.
11.D
【分析】本题考查了一元一次不等式组的整数解,求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.
先解不等式组中的每一个不等式的解集,再利用求不等式组解集的口诀“大小小大中间找”来求不等式组的解集,即可求得其整数解,然后计算加法即可得出答案.
【详解】解:
解不等式①,得,
解不等式②,得,
不等式组的解集为,
所有整数解为1、2,
所有整数解的和为.
故选D.
12.C
【分析】本题考查了解不等式组,解题的关键是掌握不等式组的解法.先求出每个不等式的解集,再确定其公共解,得到不等式组的解集,从而求其负整数解.
【详解】解:
解不等式①得:,
解不等式②:
该不等式组的解集为,
该不等式组的负整数解为,
故选:C.
13.①②④
【分析】本题主要考查一元一次不等式组的定义,熟练掌握定义并灵活运用是解题的关键.根据一元一次不等式组的定义,含有两个或两个以上的不等式,不等式中的未知数相同,并且未知数的最高次数是一次,对各选项判断后即可得解.
【详解】解:根据一元一次不等式组的定义,①②④都只含有一个未知数,并且未知数的最高次数是1,所以都是一元一次不等式组;
③含有两个未知数,
⑤含有一个未知数,但未知数的最高次数是2,
所以③⑤都不是一元一次不等式组.
故答案为:①②④.
14.36
【分析】本题考查了一元一次不等式组的应用,求一元一次不等式组的整数解,根据各数量关系正确列出不等式组是解题的关键.设共有名同学,可得图书共有本,再由每名同学分7本,那么最后一人就分不到3本,可列出不等式组,解出后并结合为正整数即可得到答案.
【详解】解:设共有名同学,则图书共有本,
由题意得,
解得:,
又为正整数,
,
当时,
故答案为:36.
15. 无解
【分析】本题考查了不等式组的解集,(1)、(2)、(3)根据同大取大,同小取小,小大大小中间找,大大小小解不了的原则直接写出解集即可.
【详解】解:(1)的解集为;
(2)的解集为;
(3)的解集为无解;
故答案为:;;无解.
16.
【分析】本题考查根据不等式组的解的情况,求参数的范围,先求出每一个不等式的解,根据不等式组有解,得到关于的不等式,进一步求解即可.
【详解】解:解,得:,
∵不等式组有解,
∴,
∴,
∴;
故答案为:.
17. /
【分析】本题考查了利用数轴求不等式组的解集,解题的关键是数形结合,并掌握不等式组解集的求法.
(1)利用数轴找到三个不等式解集的公共部分,即可求解;
(2)根据不等式组解集的情况求解即可.
【详解】解:(1)由图④可知,的取值范围是,
故答案为:;
(2)解集和没有公共部分,
的取值范围是,
故答案为:.
18.不等式组的解集为.
【分析】本题考查了一元一次不等式组的解法;首先解出不等式组中每个不等式的解集,然后找出两个不等式解集的公共部分,求出不等式组的解集即可.
【详解】解:解不等式①,得.
解不等式②,得,
∴不等式组的解集为.
19.(1),数轴见解析
(2)
(3)
(4)
【分析】本题主要考查解一元一次不等式以及一元一次不等式的解集,熟练掌握解一元一次不等式是解题的关键.
(1)解不等式将解集在数轴上表示出来即可;
(2)根据解集写出所有负整数即可;
(3)解不等式,得,由题意,得,即可得到答案;
(4)解不等式,得,根据题意得到,即可得到答案;
【详解】(1)解:解不等式,得,解集在数轴上如图所示;
(2)解:不等式的所有负整数解为;
(3)解:解不等式,得,
由题意,得,
解得;
(4)解:解不等式,得,
不等式的最小整数解为,
解不等式,
得,
根据题意,得,
解得.
20.,非负整数解有0,1,2,3
【分析】本题主要考查解一元一次不等式组,熟练掌握解一元一次不等式组的运算法则是解题的关键.分别求出每个不等式的解集,再将解集联立起来.
【详解】解:,
解不等式①,得,
解不等式②,得,
该不等式组的解集为,
该不等式组的非负整数解有0,1,2,3.
21.
【分析】本题考查了解一元一次不等式组,求代数式的值,根据不等式组的解集求出m与n的值是解题的关键;先解不等式组,根据不等式组的解集得关于m与n的方程,求出m与n的值,即可求得代数式的值.
【详解】解:令
解不等式①,得.解不等式②,得.
不等式组的解集为,
,,
解得,,
.
22..
【分析】本题主要考查解一元一次不等式组的方法,掌握不等式的性质,运用去分母、去括号、移项、合并同类项、系数化为的方法解不等式组是解题的关键.
【详解】解:去分母,得,
去括号,得,
移项、合并同类项,得,
系数化为1,得.
23.
【分析】本题考查了解一元一次不等式组,熟练掌握一元一次不等式组的解法是解题的关键,先分别求出两个不等式的解,再求出其公共部分即可.
【详解】解:解不等式①,得
,
解不等式②得,
所以不等式组的解集为.
24.数轴见解析,.
【分析】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.需要注意的是:如果是表示大于或小于号的点要用空心圆圈,如果是表示大于等于或小于等于号的点要用实心圆点.
【详解】解:解不等式①,得.
解不等式②,得,
∴不等式组的解集为.
该不等式组的解集在数轴上表示如图.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
7.3一元一次不等式组
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知不等式组的解集是,则关于的方程的解为( )
A. B. C. D.
2.不等式组的解集在数轴上的表示如图所示,则符合该解集的不等式组为( )
A. B. C. D.
3.不等式组的整数解有( )
A.1个 B.2个 C.3个 D.4个
4.不等式组的解集是( )
A. B. C. D.
5.不等式组的解集为( )
A. B. C. D.
6.把一些笔记本分给几个学生,如果每人分4本,那么余9本;如果前面的每个学生分6本,那么最后一人能分到但分不到3本,因此共有学生( )
A.5人 B.6人 C.7人 D.6人或7人
7.下列各式是一元一次不等式组的是( )
A. B. C. D.
8.不等式组的解集在数轴上表示为( )
A. B.
C. D.
9.下列不等式组中,属于一元一次不等式组的是( )
A. B.
C. D.
10.不等式组的解集在数轴上表示如图,则式子的值为( )
A. B.0 C.4 D.6
11.不等式组的整数解的和为( )
A. B. C.1 D.3
12.不等式组的负整数解是( )
A. B. C. D.
二、填空题
13.下列不等式组中,是一元一次不等式组的有 .(填序号)
① ② ③ ④ ⑤
14.把一些书分给几名同学,如果每人分5本,那么余6本;如果前面的每名同学分7本,那么最后一人可分到书但不足3本.这些书共有 本.
15.请直接写出下列不等式组的解集:
(1)的解集为 ;
(2)的解集为 ;
(3)的解集为 .
16.若关于x的不等式组有解,则m的取值范围是 .
17.图①表示的是的解集,图②表示的是的解集,图③中两个解集交叉的部分即为两个解集的公共部分.
(1)如图④,用不等式表示三个解集的公共部分,的取值范围是 ;
(2)若解集和没有公共部分,则的取值范围是 .
三、解答题
18.解不等式组:
19.已知不等式.
(1)求不等式的解集,并把解集在数轴上表示出来;
(2)求不等式的所有负整数解;
(3)若不等式的解集与不等式的解集相同,求a的值;
(4)若不等式的最小整数解也是关于不等式的解,求m的取值范围.
20.解不等式组,并写出它的非负整数解.
21.已知关于x的不等式组的解集为,求的值.
22.解不等式组:.
23.解不等式组
24.解不等式组并将解集表示在数轴上.
《7.3一元一次不等式组》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D B D B B C C C B A
题号 11 12
答案 D C
1.D
【分析】此题考查解一元一次方程,解一元一次不等式组.解题关键在于掌握其方法步骤.
解不等式组,根据其解集得出关于a、b的方程,解之求得a、b的值,再还原方程,解方程即可.
【详解】解:,
解不等式①,得;
解不等式②,得.
∵不等式组的解集是,
∴.
∴,.
∴.
∴方程为.
解得.
故选:D.
2.B
【分析】本题考查的是在数轴上表示不等式的解集以及解一元一次不等式组,先根据在数轴上表示不等式解集的方法得出该不等式组的解集,再找出符合条件的不等式组即可.
【详解】解:由数轴上表示不等式解集的方法可知,该不等式组的解集为:,
A、的解集是:,故本选项不合题意;
B、的解集是:,故本选项符合题意;
C、无解,故本选项不合题意;
D、的解集是:,故本选项不合题意.
故选:B.
3.D
【分析】本题主要考查了求不等式组的整数解,先求出每个不等式的解集,再根据夹逼原则求出不等式组的解集,进而求出不等式组的整数解个数即可.
【详解】解:解不等式组
解①式得:,
解②式得:
∴不等式组的解集为,
∴共有、0、1四个整数解.
故选:D.
4.B
【分析】本题主要考查解一元一次不等式组,首先分别解出两个不等式的解集,再根据不等式组的解集确定规律找出不等式组的解集.
【详解】解:
解不等式①得,;
解不等式②得,;
所以,不等式组的解集为:.
故选:B.
5.B
【分析】本题考查了解一元一次不等式组,解题的关键是掌握解一元一次不等式组的方法.
分别求得不等式组中每个不等式的解集,再找到两个不等式解集的公共部分即为不等式组的解集.
【详解】解:
解不等式①,得.
解不等式②,得,
∴不等式组的解集为.
故选:B.
6.C
【分析】本题考查不等式组的实际应用,设共有学生人,根据每个学生分6本,那么最后一人能分到但分不到3本,列出不等式组,求出正整数解,即可.
【详解】解:设共有学生人,由题意,得:
,
解得:,
∵人数为正整数,
∴;
故选C.
7.C
【分析】本题考查了一元一次不等式组的定义:几个含有同一个未知数的一元一次不等式组合在一起,就组成了一个一元一次不等式组,熟练掌握一元一次不等式组的定义是解题的关键.
根据一元一次不等式组的定义逐项判断即可
【详解】解:A、不是一元一次不等式组,故该选项不符合题意;
B、不是一元一次不等式组,故该选项不符合题意;
C、 是一元一次不等式组,故该选项符合题意;
D、 不是一元一次不等式组,故该选项不符合题意;
故选:C
8.C
【分析】分别求出不等式组中两不等式的解集,找出两解集的公共部分,可得不等式组的解集,再在数轴上表示出来,即可得解.
本题考查的是解一元一次不等式组,正确求出每一个不等式的解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
【详解】解:
由①得,
由②得,
∴不等式组的解集为,
将解集表示在数轴上为:
.
故选:C
9.B
【分析】本题考查了一元一次不等式组.解题的关键是掌握一元一次不等式组的定义.
一元一次不等式组中指含有一个相同的未知数,并且所含未知数的项的最高次数是1次,不等式的两边都是整式,根据以上内容判断即可.
【详解】解:A、该不等式组中含有两个未知数,不是一元一次不等式组,故本选项不符合题意;
B、该不等式组是一元一次不等式组,故本选项符合题意;
C、该不等式组中的第二个不等式是分式不等式,则它不是一元一次不等式组,故本选项不符合题意;
D、该不等式组中未知数的最高次数是2,不是一元一次不等式组,故本选项不符合题意;
故选:B.
10.A
【分析】本题主要考查了解一元一次不等式组,在数轴上表示不等式组的解集,正确根据数轴上表示的解集求出a、b的值是解题的关键.分别解两个不等式求出其对应的解集,再根据数轴表示的解集,求出a、b的值即可得到答案.
【详解】解:
解不等式①得,
解不等式②得:,
根据数轴表示的解集可知不等式组的解集为,
∴,
∴,
∴,
故选A.
11.D
【分析】本题考查了一元一次不等式组的整数解,求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.
先解不等式组中的每一个不等式的解集,再利用求不等式组解集的口诀“大小小大中间找”来求不等式组的解集,即可求得其整数解,然后计算加法即可得出答案.
【详解】解:
解不等式①,得,
解不等式②,得,
不等式组的解集为,
所有整数解为1、2,
所有整数解的和为.
故选D.
12.C
【分析】本题考查了解不等式组,解题的关键是掌握不等式组的解法.先求出每个不等式的解集,再确定其公共解,得到不等式组的解集,从而求其负整数解.
【详解】解:
解不等式①得:,
解不等式②:
该不等式组的解集为,
该不等式组的负整数解为,
故选:C.
13.①②④
【分析】本题主要考查一元一次不等式组的定义,熟练掌握定义并灵活运用是解题的关键.根据一元一次不等式组的定义,含有两个或两个以上的不等式,不等式中的未知数相同,并且未知数的最高次数是一次,对各选项判断后即可得解.
【详解】解:根据一元一次不等式组的定义,①②④都只含有一个未知数,并且未知数的最高次数是1,所以都是一元一次不等式组;
③含有两个未知数,
⑤含有一个未知数,但未知数的最高次数是2,
所以③⑤都不是一元一次不等式组.
故答案为:①②④.
14.36
【分析】本题考查了一元一次不等式组的应用,求一元一次不等式组的整数解,根据各数量关系正确列出不等式组是解题的关键.设共有名同学,可得图书共有本,再由每名同学分7本,那么最后一人就分不到3本,可列出不等式组,解出后并结合为正整数即可得到答案.
【详解】解:设共有名同学,则图书共有本,
由题意得,
解得:,
又为正整数,
,
当时,
故答案为:36.
15. 无解
【分析】本题考查了不等式组的解集,(1)、(2)、(3)根据同大取大,同小取小,小大大小中间找,大大小小解不了的原则直接写出解集即可.
【详解】解:(1)的解集为;
(2)的解集为;
(3)的解集为无解;
故答案为:;;无解.
16.
【分析】本题考查根据不等式组的解的情况,求参数的范围,先求出每一个不等式的解,根据不等式组有解,得到关于的不等式,进一步求解即可.
【详解】解:解,得:,
∵不等式组有解,
∴,
∴,
∴;
故答案为:.
17. /
【分析】本题考查了利用数轴求不等式组的解集,解题的关键是数形结合,并掌握不等式组解集的求法.
(1)利用数轴找到三个不等式解集的公共部分,即可求解;
(2)根据不等式组解集的情况求解即可.
【详解】解:(1)由图④可知,的取值范围是,
故答案为:;
(2)解集和没有公共部分,
的取值范围是,
故答案为:.
18.不等式组的解集为.
【分析】本题考查了一元一次不等式组的解法;首先解出不等式组中每个不等式的解集,然后找出两个不等式解集的公共部分,求出不等式组的解集即可.
【详解】解:解不等式①,得.
解不等式②,得,
∴不等式组的解集为.
19.(1),数轴见解析
(2)
(3)
(4)
【分析】本题主要考查解一元一次不等式以及一元一次不等式的解集,熟练掌握解一元一次不等式是解题的关键.
(1)解不等式将解集在数轴上表示出来即可;
(2)根据解集写出所有负整数即可;
(3)解不等式,得,由题意,得,即可得到答案;
(4)解不等式,得,根据题意得到,即可得到答案;
【详解】(1)解:解不等式,得,解集在数轴上如图所示;
(2)解:不等式的所有负整数解为;
(3)解:解不等式,得,
由题意,得,
解得;
(4)解:解不等式,得,
不等式的最小整数解为,
解不等式,
得,
根据题意,得,
解得.
20.,非负整数解有0,1,2,3
【分析】本题主要考查解一元一次不等式组,熟练掌握解一元一次不等式组的运算法则是解题的关键.分别求出每个不等式的解集,再将解集联立起来.
【详解】解:,
解不等式①,得,
解不等式②,得,
该不等式组的解集为,
该不等式组的非负整数解有0,1,2,3.
21.
【分析】本题考查了解一元一次不等式组,求代数式的值,根据不等式组的解集求出m与n的值是解题的关键;先解不等式组,根据不等式组的解集得关于m与n的方程,求出m与n的值,即可求得代数式的值.
【详解】解:令
解不等式①,得.解不等式②,得.
不等式组的解集为,
,,
解得,,
.
22..
【分析】本题主要考查解一元一次不等式组的方法,掌握不等式的性质,运用去分母、去括号、移项、合并同类项、系数化为的方法解不等式组是解题的关键.
【详解】解:去分母,得,
去括号,得,
移项、合并同类项,得,
系数化为1,得.
23.
【分析】本题考查了解一元一次不等式组,熟练掌握一元一次不等式组的解法是解题的关键,先分别求出两个不等式的解,再求出其公共部分即可.
【详解】解:解不等式①,得
,
解不等式②得,
所以不等式组的解集为.
24.数轴见解析,.
【分析】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.需要注意的是:如果是表示大于或小于号的点要用空心圆圈,如果是表示大于等于或小于等于号的点要用实心圆点.
【详解】解:解不等式①,得.
解不等式②,得,
∴不等式组的解集为.
该不等式组的解集在数轴上表示如图.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
