8.1幂的运算同步练习(含解析)
图片预览



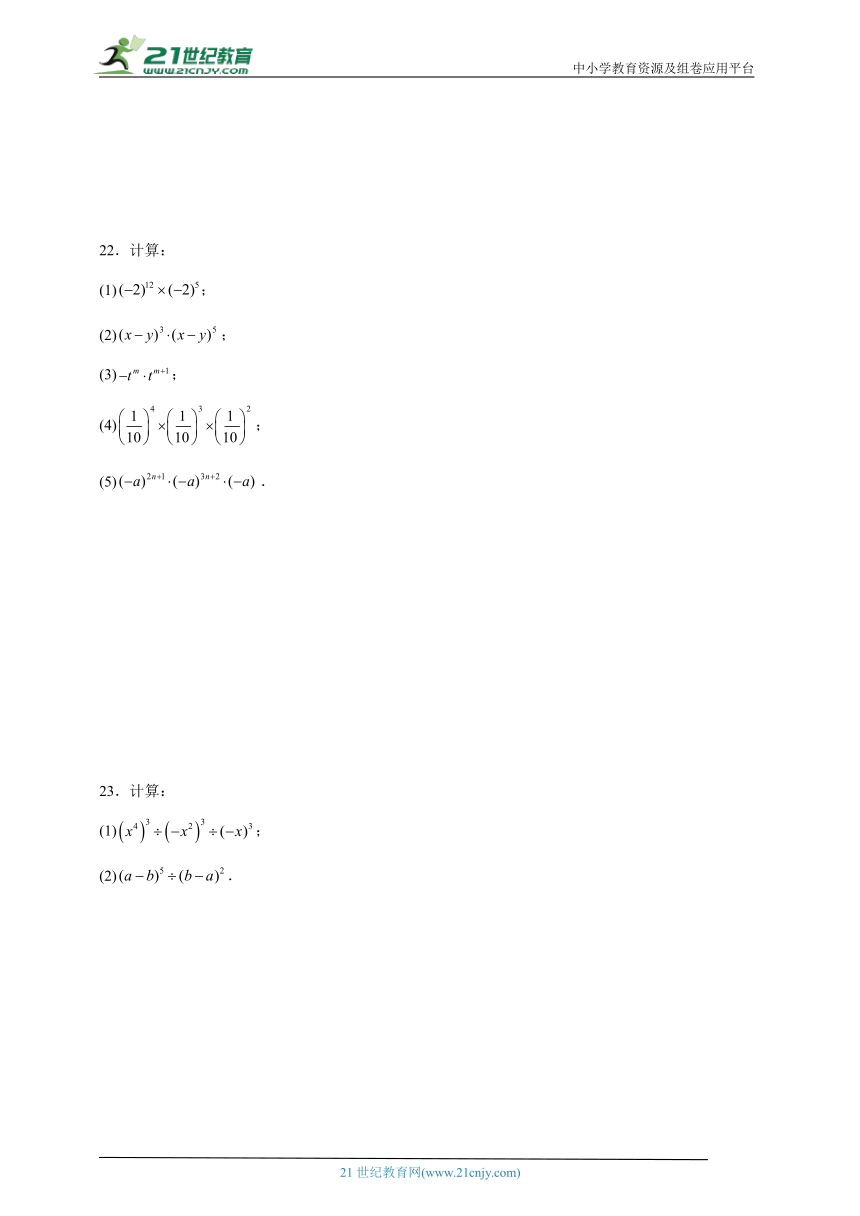
文档简介
中小学教育资源及组卷应用平台
8.1幂的运算
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列运算中,正确的是( )
A.(是正整数) B.(是正整数)
C. D.
2.广阔无垠的太空中有无数颗恒星,其中罗斯248星离太阳系的距离约光年.光年是天文学中一种计量天体时空距离的长度单位,表示光在一年中所通过的距离,已知1光年约为千米,则罗斯248星距离太阳系约为( )千米.
A. B. C. D.
3.计算的结果是( )
A. B. C. D.
4.若,则的值是( )
A.1 B.2 C.3 D.5
5.下列算式中,正确的有( )
①;②;③;④;⑤.
A.1个 B.2个 C.3个 D.4个
6.计算的结果是( )
A.0 B. C. D.
7.计算的结果是( )
A. B. C. D.
8.可以写成( )
A. B. C. D.
9.若,则n的值为( )
A.1 B.2 C.3 D.4
10.有下列算式:①(是正整数);②;③;④.其中,正确的有( )
A.1个 B.2个 C.3个 D.4个
11.若,则等于( )
A.a B. C. D.
12.下列计算正确的是( )
A. B.
C. D.
二、填空题
13.(1) ;
(2) ;
(3) ;
(4) ;
(5) ;
(6) .
14.用科学记数法表示下列各数:
(1) ;(2) ;(3) ;(4) .
15.信息技术的存储设备常用等作为存储量的单位,其中,.对于一个存储量是的闪存盘,其容量有 B(结果写成乘方的形式).
16.已知,则的值为 .
17.现规定一种新运算“※”:.如,则 , .
三、解答题
18.试说明:(m为正整数)能被17整除.
19.已知,求的值.
20.已知,,,求下列代数式的值:
(1);
(2).
21.已知(是正整数),求的值.
22.计算:
(1);
(2);
(3);
(4);
(5).
23.计算:
(1);
(2).
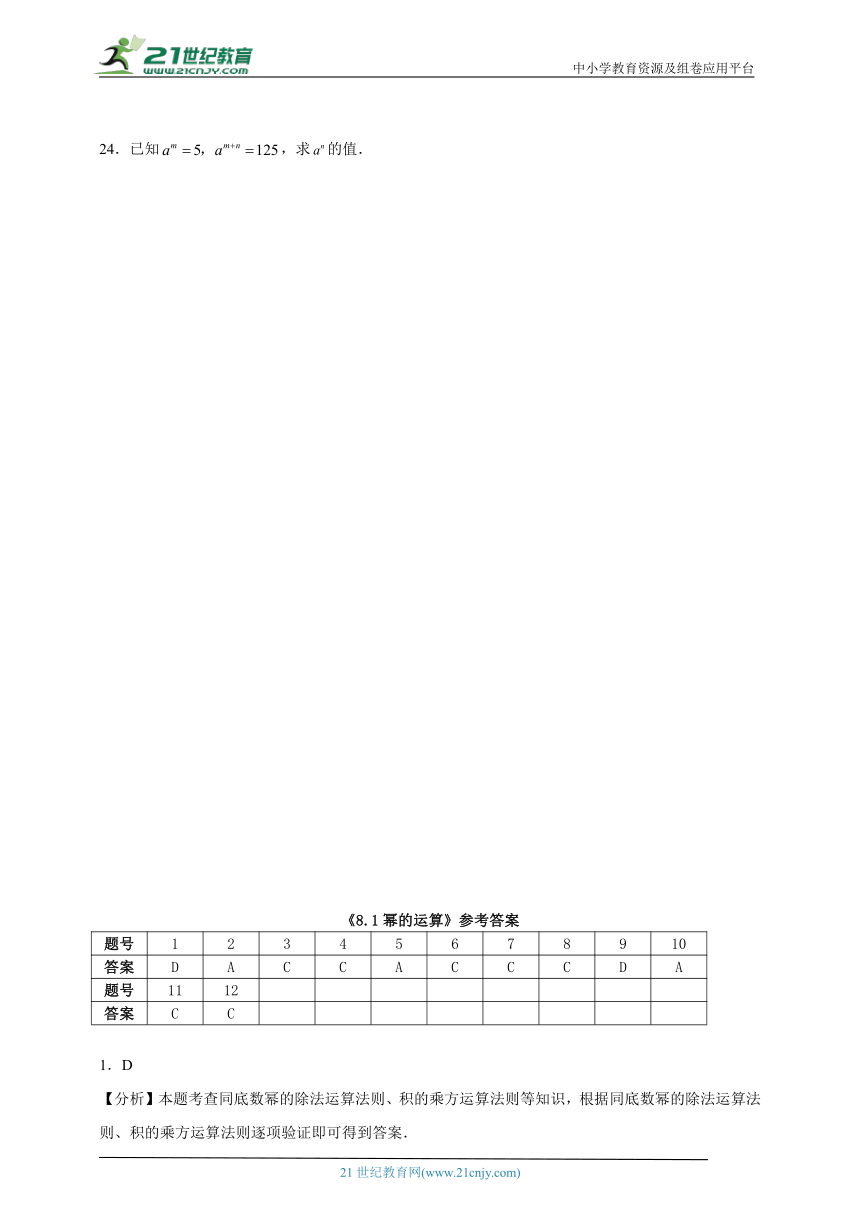
24.已知,求的值.
《8.1幂的运算》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D A C C A C C C D A
题号 11 12
答案 C C
1.D
【分析】本题考查同底数幂的除法运算法则、积的乘方运算法则等知识,根据同底数幂的除法运算法则、积的乘方运算法则逐项验证即可得到答案.
【详解】解:A、,选项计算错误,不符合题意;
B、,选项计算错误,不符合题意;
C、,选项计算错误,不符合题意;
D、,选项计算正确,符合题意;
故选:D.
2.A
【分析】本题考查了有理数乘法的应用,同底数幂的乘法,根据同底数幂的乘法进行计算即可.
【详解】解:,
故选:A.
3.C
【分析】本题考查了同底数幂的除法运算,掌握其运算法则是解题的关键.
根据同底数幂的除法运算法则“底数不变,指数相减”计算即可.
【详解】解:,
故选:C .
4.C
【分析】本题主要考查了同底数幂的除法,熟练掌握同底数幂的除法运算法则是解题的关键.
根据即可确定.
【详解】解:,
∵,
∴,
故选:C.
5.A
【分析】本题主要考查了同底数幂乘法、合并同类项;熟练掌握相关运算法则是解题关键.
【详解】解:①,错误;
②和不是同类项,不能合并,错误;
③,错误;
④,错误;
⑤,正确.
所以正确的有1个.
故选A.
6.C
【分析】本题考查的是积的乘方和同底数幂乘法运算,熟练掌握运算法则是解题的关键;
直接利用积的乘方和同底数幂乘法运算法则计算即可.
【详解】解:
.
7.C
【分析】本题考查了积的乘方运算,掌握积的乘方和幂的乘方运算法则是解题的关键.
根据积的乘方和幂的乘方运算法则计算即可求解.
【详解】解:,
故选:C.
8.C
【分析】本题考查了同底数幂的乘法的逆用,根据同底数幂的乘法法则即可得解,熟练掌握同底数幂的乘法法则是解此题的关键.
【详解】解:,
故选:C.
9.D
【分析】本题主要考查了积的乘方计算,根据积的乘方计算法则可得,据此可得答案.
【详解】解:∵,
∴,
∴,
∴,
故选:D.
10.A
【分析】本题考查了同底数幂的乘法,幂的乘方,积的乘方,根据幂的相关运算法则,逐一进行判断即可.
【详解】解:①,正确;
②,原计算错误;
③,原计算错误;
④,原计算错误.
故选:A.
11.C
【分析】本题考查了同底数幂的乘法运算,由同底数幂的乘法运算得,即可求解;掌握是解题的关键.
【详解】解:,,
;
故选:C.
12.C
【分析】本题考查了同底数幂的除法运算,掌握其运算法则是解题的关键.
根据同底数幂的除法运算法则“底数不变,指数相减”计算即可求解.
【详解】解:A、,原选项计算错误,不符合题意;
B、,原选项计算错误,不符合题意;
C、,正确,符合题意;
D、,原选项计算错误,不符合题意.
故选:C .
13. 4
【分析】本题考查同底数幂的除法运算、积的乘方运算及乘方运算等知识,熟记相关运算法则是解决问题的关键.
(1)先由同底数幂的除法运算化简,再由乘方运算求解即可得到答案;
(2)由同底数幂的除法运算求解即可得到答案;
(3)先由同底数幂的除法运算化简,再由乘方运算求解即可得到答案;
(4)先由同底数幂的除法运算化简,再由乘方运算求解即可得到答案;
(5)先由同底数幂的除法运算化简,再由积的乘方运算求解即可得到答案;
(6)先由同底数幂的除法运算化简,再由乘方运算求解即可得到答案.
【详解】解:(1);
(2);
(3);
(4);
(5);
(6);
故答案为:(1);(2);(3);(4);(5);(6)4.
14.
【分析】本题主要考查了科学记数法表示绝对值小于(大于)1的数,先确定a,n,再写成的形式,其中,n为负(正)整数.
【详解】解:根据题意,得,,,.
故答案为:,,.
15.
【分析】本题考查了同底数幂的乘法,熟练掌握同底数幂的乘法法则是解决本题的关键.
根据乘方的定义,得.再根据同底数幂的乘法法则(m,n是正整数),可得答案.
【详解】解:∵,,,
∴.
故答案为:.
16.12
【分析】本题考查了同底数幂的乘法运算,根据题意,把变形为,即可得出答案.
【详解】解:解:∵,
∴=6×2 =12.
故答案为:12.
17. / /
【分析】本题主要考查定义新运算,观察新运算规律,将运算的式子转化为常规运算是解题的关键.根据新运算的规定,知,,再根据有理数的乘方运算法则和积的乘方运算法则计算即可.
【详解】解:∵,
∴.
.
故答案为:,.
18.见解析
【分析】本题考查了积的乘方、幂的乘方,和同底数幂的乘法,熟练掌握运算法则是解题的关键
根据幂的乘方、积的乘方、同底数幂的乘法及乘法分配律的运算法则,把已知式子化为,从而得出结论.
【详解】解:原式
,
所以(m为正整数)能被17整除.
19.
【分析】本题考查同底数幂的除法,逆用幂的乘方,根据,得到,再根据同底数幂的除法,逆用幂的乘方法则计算,即可.
【详解】解:因为,
所以,
所以,
所以.
20.(1)15
(2)400
【分析】本题主要考查了同底数幂的乘法的逆用以及幂的乘方的逆用与积的乘方的逆用,熟记幂的运算法则是解答本题的关键.
(1)根据幂的乘方运算法则可得,,再根据同底数幂的乘法法则计算即可;
(2)根据积的乘方和幂的乘方运算法则计算即可.
【详解】(1)解:由题意,得,,
原式.
(2)解:原式.
21.2048
【分析】本题主要考查同底数幂乘法的逆用,熟练掌握运算法则是解题的关键.根据题意得到,即可得到答案.
【详解】解:,
.
22.(1)
(2)
(3)
(4)
(5)
【分析】本题考查了同底数幂的乘法,熟练掌握同底数幂的乘法法则:底数不变,指数相加是解此题的关键.
(1)根据同底数幂的乘法法则计算即可得解;
(2)根据同底数幂的乘法法则计算即可得解;
(3)根据同底数幂的乘法法则计算即可得解;
(4)根据同底数幂的乘法法则计算即可得解;
(5)根据同底数幂的乘法法则计算即可得解.
【详解】(1)解:原式;
(2)解:原式;
(3)解:原式;
(4)解:原式;
(5)解:原式.
23.(1)
(2)
【分析】本题考查同底数幂的除法运算、幂的乘方运算等知识,熟记相关运算法则是解决问题的关键.
(1)先计算幂的乘方运算,再由由同底数幂的除法运算法则求解即可得到答案;
(2)先由偶次方的性质恒等变形,再由同底数幂的除法运算求解即可得到答案.
【详解】(1)解:
;
(2)解:
.
24.25
【分析】本题考查了同底数幂乘法的逆用,根据计算即可.
【详解】解:因为,
所以.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
8.1幂的运算
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列运算中,正确的是( )
A.(是正整数) B.(是正整数)
C. D.
2.广阔无垠的太空中有无数颗恒星,其中罗斯248星离太阳系的距离约光年.光年是天文学中一种计量天体时空距离的长度单位,表示光在一年中所通过的距离,已知1光年约为千米,则罗斯248星距离太阳系约为( )千米.
A. B. C. D.
3.计算的结果是( )
A. B. C. D.
4.若,则的值是( )
A.1 B.2 C.3 D.5
5.下列算式中,正确的有( )
①;②;③;④;⑤.
A.1个 B.2个 C.3个 D.4个
6.计算的结果是( )
A.0 B. C. D.
7.计算的结果是( )
A. B. C. D.
8.可以写成( )
A. B. C. D.
9.若,则n的值为( )
A.1 B.2 C.3 D.4
10.有下列算式:①(是正整数);②;③;④.其中,正确的有( )
A.1个 B.2个 C.3个 D.4个
11.若,则等于( )
A.a B. C. D.
12.下列计算正确的是( )
A. B.
C. D.
二、填空题
13.(1) ;
(2) ;
(3) ;
(4) ;
(5) ;
(6) .
14.用科学记数法表示下列各数:
(1) ;(2) ;(3) ;(4) .
15.信息技术的存储设备常用等作为存储量的单位,其中,.对于一个存储量是的闪存盘,其容量有 B(结果写成乘方的形式).
16.已知,则的值为 .
17.现规定一种新运算“※”:.如,则 , .
三、解答题
18.试说明:(m为正整数)能被17整除.
19.已知,求的值.
20.已知,,,求下列代数式的值:
(1);
(2).
21.已知(是正整数),求的值.
22.计算:
(1);
(2);
(3);
(4);
(5).
23.计算:
(1);
(2).
24.已知,求的值.
《8.1幂的运算》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D A C C A C C C D A
题号 11 12
答案 C C
1.D
【分析】本题考查同底数幂的除法运算法则、积的乘方运算法则等知识,根据同底数幂的除法运算法则、积的乘方运算法则逐项验证即可得到答案.
【详解】解:A、,选项计算错误,不符合题意;
B、,选项计算错误,不符合题意;
C、,选项计算错误,不符合题意;
D、,选项计算正确,符合题意;
故选:D.
2.A
【分析】本题考查了有理数乘法的应用,同底数幂的乘法,根据同底数幂的乘法进行计算即可.
【详解】解:,
故选:A.
3.C
【分析】本题考查了同底数幂的除法运算,掌握其运算法则是解题的关键.
根据同底数幂的除法运算法则“底数不变,指数相减”计算即可.
【详解】解:,
故选:C .
4.C
【分析】本题主要考查了同底数幂的除法,熟练掌握同底数幂的除法运算法则是解题的关键.
根据即可确定.
【详解】解:,
∵,
∴,
故选:C.
5.A
【分析】本题主要考查了同底数幂乘法、合并同类项;熟练掌握相关运算法则是解题关键.
【详解】解:①,错误;
②和不是同类项,不能合并,错误;
③,错误;
④,错误;
⑤,正确.
所以正确的有1个.
故选A.
6.C
【分析】本题考查的是积的乘方和同底数幂乘法运算,熟练掌握运算法则是解题的关键;
直接利用积的乘方和同底数幂乘法运算法则计算即可.
【详解】解:
.
7.C
【分析】本题考查了积的乘方运算,掌握积的乘方和幂的乘方运算法则是解题的关键.
根据积的乘方和幂的乘方运算法则计算即可求解.
【详解】解:,
故选:C.
8.C
【分析】本题考查了同底数幂的乘法的逆用,根据同底数幂的乘法法则即可得解,熟练掌握同底数幂的乘法法则是解此题的关键.
【详解】解:,
故选:C.
9.D
【分析】本题主要考查了积的乘方计算,根据积的乘方计算法则可得,据此可得答案.
【详解】解:∵,
∴,
∴,
∴,
故选:D.
10.A
【分析】本题考查了同底数幂的乘法,幂的乘方,积的乘方,根据幂的相关运算法则,逐一进行判断即可.
【详解】解:①,正确;
②,原计算错误;
③,原计算错误;
④,原计算错误.
故选:A.
11.C
【分析】本题考查了同底数幂的乘法运算,由同底数幂的乘法运算得,即可求解;掌握是解题的关键.
【详解】解:,,
;
故选:C.
12.C
【分析】本题考查了同底数幂的除法运算,掌握其运算法则是解题的关键.
根据同底数幂的除法运算法则“底数不变,指数相减”计算即可求解.
【详解】解:A、,原选项计算错误,不符合题意;
B、,原选项计算错误,不符合题意;
C、,正确,符合题意;
D、,原选项计算错误,不符合题意.
故选:C .
13. 4
【分析】本题考查同底数幂的除法运算、积的乘方运算及乘方运算等知识,熟记相关运算法则是解决问题的关键.
(1)先由同底数幂的除法运算化简,再由乘方运算求解即可得到答案;
(2)由同底数幂的除法运算求解即可得到答案;
(3)先由同底数幂的除法运算化简,再由乘方运算求解即可得到答案;
(4)先由同底数幂的除法运算化简,再由乘方运算求解即可得到答案;
(5)先由同底数幂的除法运算化简,再由积的乘方运算求解即可得到答案;
(6)先由同底数幂的除法运算化简,再由乘方运算求解即可得到答案.
【详解】解:(1);
(2);
(3);
(4);
(5);
(6);
故答案为:(1);(2);(3);(4);(5);(6)4.
14.
【分析】本题主要考查了科学记数法表示绝对值小于(大于)1的数,先确定a,n,再写成的形式,其中,n为负(正)整数.
【详解】解:根据题意,得,,,.
故答案为:,,.
15.
【分析】本题考查了同底数幂的乘法,熟练掌握同底数幂的乘法法则是解决本题的关键.
根据乘方的定义,得.再根据同底数幂的乘法法则(m,n是正整数),可得答案.
【详解】解:∵,,,
∴.
故答案为:.
16.12
【分析】本题考查了同底数幂的乘法运算,根据题意,把变形为,即可得出答案.
【详解】解:解:∵,
∴=6×2 =12.
故答案为:12.
17. / /
【分析】本题主要考查定义新运算,观察新运算规律,将运算的式子转化为常规运算是解题的关键.根据新运算的规定,知,,再根据有理数的乘方运算法则和积的乘方运算法则计算即可.
【详解】解:∵,
∴.
.
故答案为:,.
18.见解析
【分析】本题考查了积的乘方、幂的乘方,和同底数幂的乘法,熟练掌握运算法则是解题的关键
根据幂的乘方、积的乘方、同底数幂的乘法及乘法分配律的运算法则,把已知式子化为,从而得出结论.
【详解】解:原式
,
所以(m为正整数)能被17整除.
19.
【分析】本题考查同底数幂的除法,逆用幂的乘方,根据,得到,再根据同底数幂的除法,逆用幂的乘方法则计算,即可.
【详解】解:因为,
所以,
所以,
所以.
20.(1)15
(2)400
【分析】本题主要考查了同底数幂的乘法的逆用以及幂的乘方的逆用与积的乘方的逆用,熟记幂的运算法则是解答本题的关键.
(1)根据幂的乘方运算法则可得,,再根据同底数幂的乘法法则计算即可;
(2)根据积的乘方和幂的乘方运算法则计算即可.
【详解】(1)解:由题意,得,,
原式.
(2)解:原式.
21.2048
【分析】本题主要考查同底数幂乘法的逆用,熟练掌握运算法则是解题的关键.根据题意得到,即可得到答案.
【详解】解:,
.
22.(1)
(2)
(3)
(4)
(5)
【分析】本题考查了同底数幂的乘法,熟练掌握同底数幂的乘法法则:底数不变,指数相加是解此题的关键.
(1)根据同底数幂的乘法法则计算即可得解;
(2)根据同底数幂的乘法法则计算即可得解;
(3)根据同底数幂的乘法法则计算即可得解;
(4)根据同底数幂的乘法法则计算即可得解;
(5)根据同底数幂的乘法法则计算即可得解.
【详解】(1)解:原式;
(2)解:原式;
(3)解:原式;
(4)解:原式;
(5)解:原式.
23.(1)
(2)
【分析】本题考查同底数幂的除法运算、幂的乘方运算等知识,熟记相关运算法则是解决问题的关键.
(1)先计算幂的乘方运算,再由由同底数幂的除法运算法则求解即可得到答案;
(2)先由偶次方的性质恒等变形,再由同底数幂的除法运算求解即可得到答案.
【详解】(1)解:
;
(2)解:
.
24.25
【分析】本题考查了同底数幂乘法的逆用,根据计算即可.
【详解】解:因为,
所以.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
