第二十二章四边形同步练习（含解析）

中小学教育资源及组卷应用平台
第二十二章四边形
学校:___________姓名：___________班级：___________考号：___________
一、单选题
1．一个正六边形的内角和的度数为（　　）
A．1080° B．720° C．540° D．360°
2．如图，在菱形中，，则的度数为（ ）
A． B． C． D．
3．中，点D、E、F分别为边的中点，作．若的面积是12，则的面积是（ ）
A．2 B．3 C．4 D．6
4．用边长相等的下列两种正多边形，不能进行平面镶嵌的是（ ）
A．等边三角形和正六边形 B．正方形和正八边形
C．正五边形和正十边形 D．正六边形和正十二边形
5．下列命题是真命题的是（ ）
A．对角线相等的四边形是平行四边形 B．对角线互相平分且相等的四边形是平行四边形
C．对角线互相平分的四边形是平行四边形 D．对角线互相垂直的四边形是平行四边形
6．如图，在矩形中，两条对角线交于点O，，则长为（　　）
A． B．3 C． D．6
7．如图，正方形的顶点、的坐标分别为，，则点的坐标为（ ）
A． B． C． D．
8．在中，，平分交于点E，平分交于点F，且，则的长为（ ）
A．4 B．6 C．6或8 D．4或6
9．已知：如图，、分别是的中线和角平分线，，，的长为（ ）
A．10 B． C． D．
10．矩形、菱形、正方形都具有的性质是（ ）
A．对角线相等 B．对角线互相平分 C．对角线互相垂直 D．对角线互相平分且相等
11．如图，已知，添加下列条件，不能判定四边形是平行四边形的是（ ）
A． B． C． D．
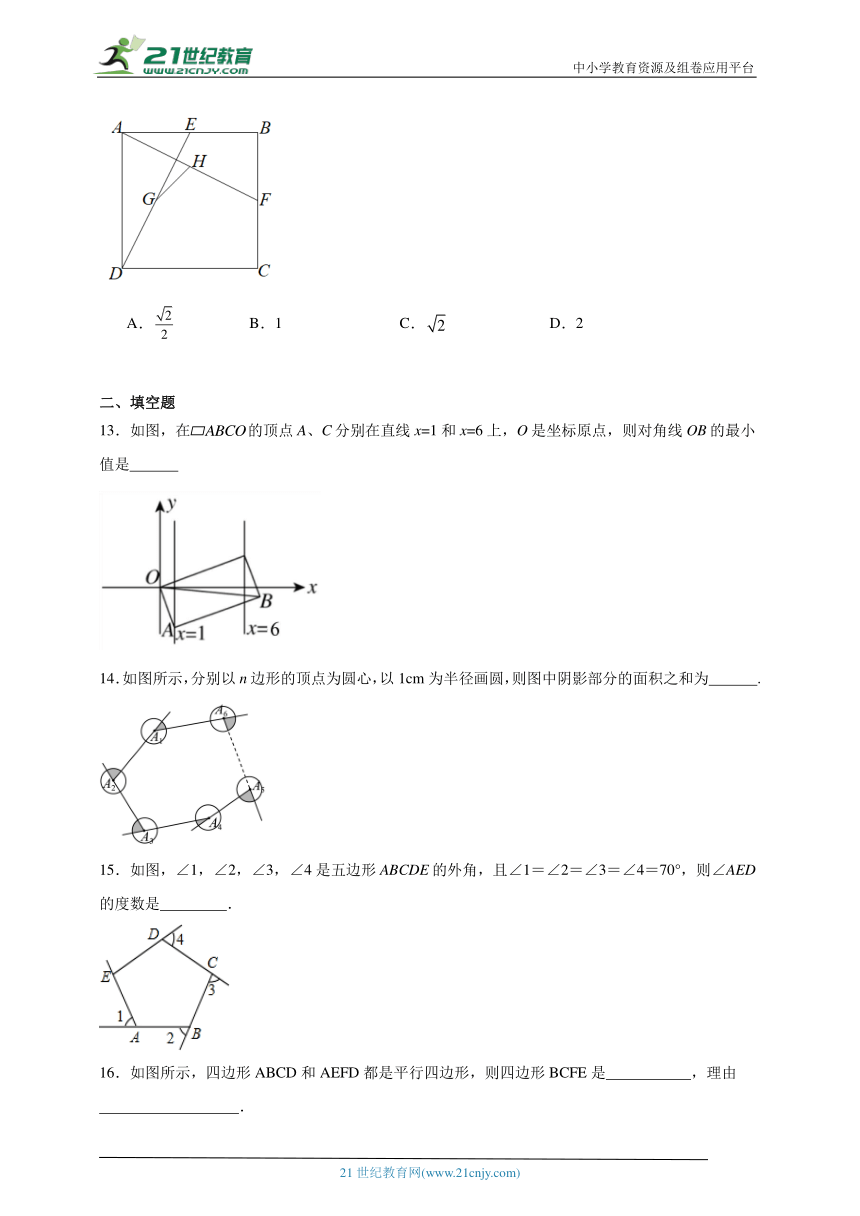
12．如图，在正方形中，，E，F分别为边的中点，连接，点G，H分别为的中点，连接，则的长为（ ）
A． B．1 C． D．2
二、填空题
13．如图，在 的顶点A、C分别在直线x=1和x=6上，O是坐标原点，则对角线OB的最小值是
14．如图所示，分别以n边形的顶点为圆心，以1cm为半径画圆，则图中阴影部分的面积之和为 .
15．如图，∠1，∠2，∠3，∠4是五边形ABCDE的外角，且∠1＝∠2＝∠3＝∠4＝70°，则∠AED的度数是 ．
16．如图所示，四边形ABCD和AEFD都是平行四边形，则四边形BCFE是 ，理由
．
17．如图，在中，D、E、F分别是的中点．若的面积为3，则的面积为 ．
三、解答题
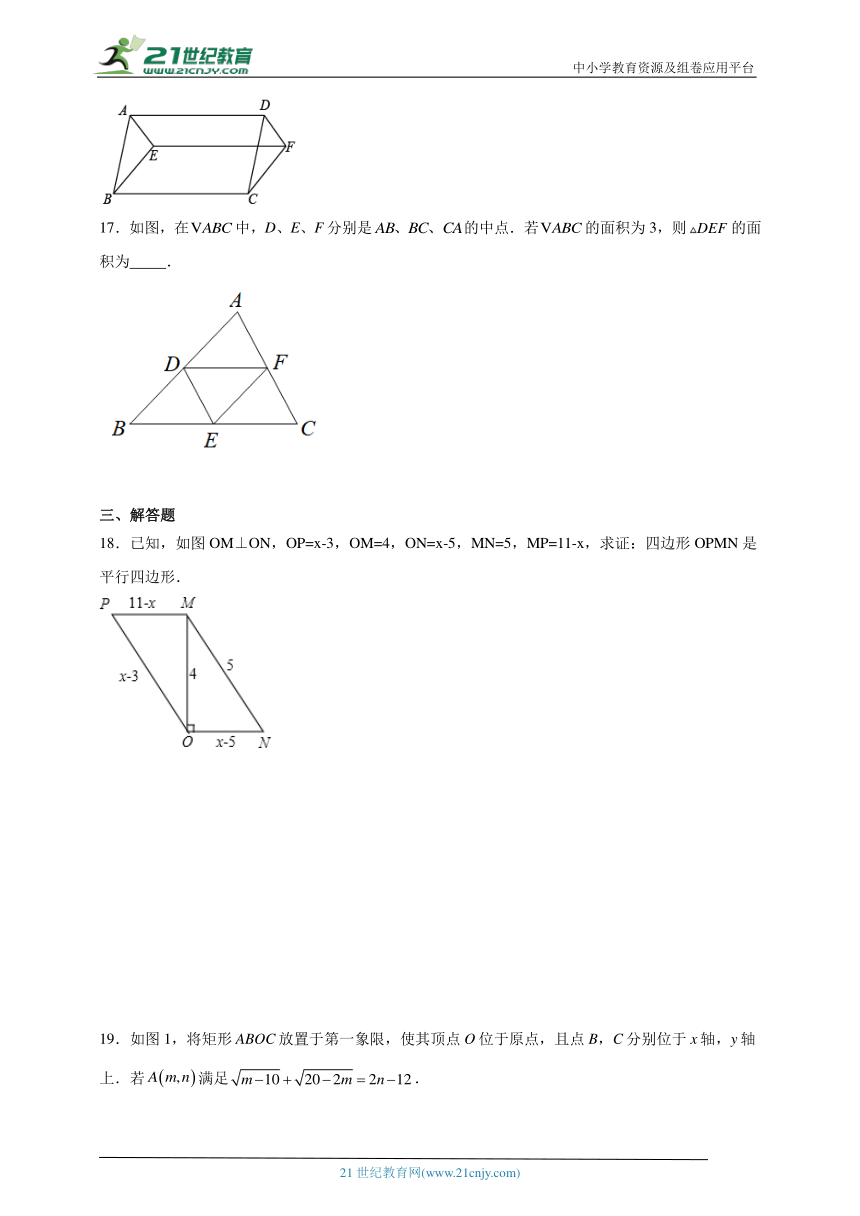
18．已知，如图OM⊥ON，OP=x-3，OM=4，ON=x-5，MN=5，MP=11-x，求证：四边形OPMN是平行四边形．
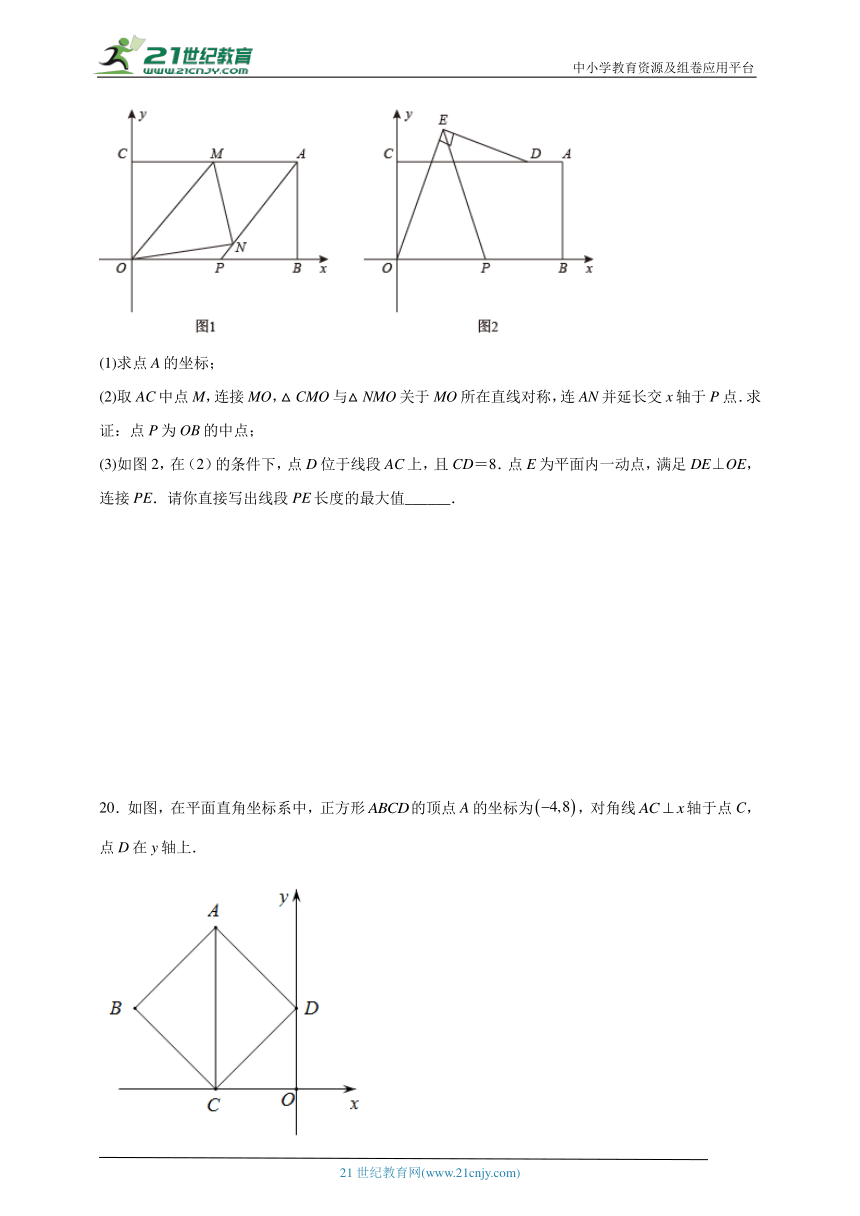
19．如图1，将矩形ABOC放置于第一象限，使其顶点O位于原点，且点B，C分别位于x轴，y轴上．若满足．
(1)求点A的坐标；
(2)取AC中点M，连接MO，△CMO与△NMO关于MO所在直线对称，连AN并延长交x轴于P点．求证：点P为OB的中点；
(3)如图2，在（2）的条件下，点D位于线段AC上，且CD＝8．点E为平面内一动点，满足DE⊥OE，连接PE．请你直接写出线段PE长度的最大值______．
20．如图，在平面直角坐标系中，正方形的顶点A的坐标为，对角线轴于点C，点D在y轴上．
（1）求点B的坐标；
（2）求直线的解析式．
21．如果一个多边形的每一个外角都等于20度，那么这个多边形的内角和是多少度？
22．在中，，，D为上一点，满足．

(1)如图1，若，直接写出的长为 ；
(2)如图2，E在的延长线上，连接，点D关于的对称点为F，连接，，若恰有成立．
①求证：；
②点G为线段上一点（不与A，C重合），连接，写出一个k的值，使得命题“如果，那么”，成立，并证明．
23．思思同学在平时的数学学习中喜欢钻研和思考问题，他想要证明命题“被一条对角线平分一个内角的平行四边形是菱形”是真命题，于是她先作了如图所示的四边形，并写出了不完整的已知和求证．
已知：如图，在平行四边形中，连接，　　　平分．求证：四边形是　　　．
(1)填空，补全已知和求证；
(2)按思思同学的想法完成证明过程．
24．如图，在中，点是边上的一点，点是的中点，过点作的平行线交的延长线于点，且，连接．
（1）判断并证明四边形的形状；
（2）当满足什么条件时，四边形是矩形？请说明理由．
《第二十二章四边形》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B C B D C C B D B B
题号 11 12
答案 C C
1．B
【分析】利用多边形的内角和定理解答即可．
【详解】解：一个正六边形的内角和的度数为：（6﹣2）×180°＝720°，
故选：B．
【点睛】本题主要考查了多边形的内角和，利用多边形的内角和定理解答是解题的关键．
2．C
【分析】本题考查了菱形的性质，先根据菱形的对边平行和直线平行的性质得到，然后根据菱形的每一条对角线平分一组对角求解．
【详解】解：四边形为菱形，
，
，
四边形为菱形，
平分，
故选：C．
3．B
【分析】过A作AH⊥BC于H，取BH中点为G，连结DG，EM⊥DF于M，根据三角形的中位线性质可得，，DF∥BC，由D、G为AB、BH中点，可得DG∥AH，且DG=，根据平行线间的距离处处相等可得DG=ME=，利用三角形面积公式S△ABC=，再求即可．
【详解】解：过A作AH⊥BC于H，取BH中点为G，连结DG，EM⊥DF于M，
∵、分别是的、边的中点，
∴，DF∥BC，
∵D、G为AB、BH中点，
∴DG∥AH，且DG=，
∵AH⊥BC
∴DG⊥BC，
∵DF∥BC，EM⊥DF
∴DG⊥DF，
∴DG=ME=
∵S△ABC=
∴．
故选择B．
【点睛】本题考查了三角形的面积，主要利用了三角形的中位线性质，平行线间的距离性质，熟练掌握三角形的中位线性质，三角形的面积，平行线间的距离性质是解题关键．
4．D
【分析】分别求出各个正多边形每个内角的度数，再结合镶嵌的条件即可作出判断．
【详解】A、正三角形的每个内角是60°，正六边形的每个内角是120°，∵2×60°+2×120°=360°，能密铺；
B、正八边形的每个内角是135°，正方形的每个内角是90°，∵2×135°+90°=360°，能密铺，；
C、正五形的每个内角是108°，正十边形的每个内角是144°，∵2×108°+144°=360°，能密铺，；
D、正六边形的每个内角是120°和正十二边形的每个内角是150°，120m+150n=360°，m=3﹣n，显然n取任何正整数时，m不能得正整数，故不能铺满．
故选D．
【点睛】本题考查平面镶嵌（密铺），关键是掌握平面镶嵌（密铺）的条件.
5．C
【分析】根据对角线互相平分的四边形是平行四边形；对角线互相平分且相等的四边形是矩形；对角线互相平分的四边形是平行四边形;对角线互相垂直平分的四边形是菱形,即可做出解答．
【详解】解：A、对角线相等的四边形是平行四边形，说法错误，应是对角线互相平分的四边形是平行四边形；B、对角线互相平分且相等的四边形是平行四边形，说法错误，应是矩形；C、对角线互相平分的四边形是平行四边形，说法正确；D、对角线互相垂直平分的四边形不一定是平行四边形，错误；故选C.
【点睛】本题主要考查了平行四边形，以及特殊的平行四边形的判定，关键是熟练掌握各种四边形的判定方法.
6．C
【分析】本题考查矩形的性质、等边三角形的判定与性质，根据矩形的性质和等边三角形的判定和性质，可以得到的长，再根据勾股定理，即可得到的长，本题得以解决．
【详解】解：∵，
∴，
∵四边形是矩形，
∴，
∴是等边三角形，
∴，
∵，
∴，
∴，
故选：C．
7．B
【分析】本题考查了全等三角形的判定和性质、正方形的性质等知识，解题的关键是学会添加垂线的辅助线，构造全等三角形解决问题．作轴交于点，用全等三角形判定定理推出，得出和的长，即可得出点的坐标．
【详解】解：如图，作轴交于点，
点、的坐标分别为，，
，，
正方形，
，，
，
，
，
，
，
轴，
，
，
，
，，
，
点的坐标为．
故选：B．
8．D
【分析】本题考查平行四边形的性质及等腰三角形的判定，根据平行加角平分线，得到，均为等腰三角形，分点F在点E的左侧和右侧，两种情况进行讨论求解即可．
【详解】解：∵四边形是平行四边形，
∴，
∴，
∵平分，平分，
∴，
∴，
如图①，当点F在点E的左侧时：，
∴；
如图②，当点F在点E的右侧时，，
∴
综上：或；
故选：D．
9．B
【分析】取的中点F，连接，，则，为中点，在中求出的长度，根据已知条件易知为中点，因此为中点，则．
【详解】解：取的中点F，连接，
是的中线，
∴，，
∵，
，
，
∴，
是的角平分线，，
，，
，
，
为中点，
为中点，
．
故选：B．
【点睛】本题考查了三角形中线和角平分线的性质以及勾股定理的应用，作出辅助线构建直角三角形是解题的关键．
10．B
【分析】矩形、菱形、正方形都是特殊的平行四边形，因而平行四边形的性质就是四个图形都具有的性质．
【详解】解：平行四边形的对角线互相平分，而对角线相等、平分一组对角、互相垂直不一定成立．
故平行四边形、矩形、菱形、正方形都具有的性质是：对角线互相平分．
故选B．
【点睛】本题主要考查了正方形、矩形、菱形、平行四边形的性质，理解四个图形之间的关系是解题关键．
11．C
【分析】本题考查平行四边形的判定，根据平行四边形的判定方法，逐一进行判断即可．掌握平行四边形的判定方法，是解题的关键．
【详解】解：A、，
，
，
，
，
四边形是平行四边形，故选项A不符合题意；
B、，
，
，
，
，
四边形是平行四边形，故选项B不符合题意；
C、，
，不能判定四边形是平行四边形，故选项C符合题意；
D、，
，
又∵，
四边形是平行四边形，故选项D不符合题意；
故选：C．
12．C
【分析】连接AG，延长AG交CD于M，连接FM，由正方形ABCD推出AB＝CD＝BC＝AD＝4，ABCD，∠C＝90°，证明△AEG≌△MDG，得到AG＝MG，AE＝DM＝AB＝CD，根据三角形中位线定理得到GH＝FM，由勾股定理求出FM即可得到GH．
【详解】解：连接AG，延长AG交CD于M，连接FM，
∵四边形ABCD是正方形，
∴AB＝CD＝BC＝AD＝4，ABCD，∠C＝90°，
∴∠AEG＝∠GDM，∠EAG＝∠DMG，
∵G为DE的中点，
∴GE＝GD，
∴△AEG≌△MDG（AAS），
∴AG＝MG，AE＝DM＝AB＝CD，
∴CM＝CD＝2，
∵点H为AF的中点，
∴GH＝FM，
∵F为BC的中点，
∴CF＝BC＝2，
∴FM＝，
∴GH＝FM＝，
故选：C．
【点睛】本题主要考查了正方形的性质，全等三角形的判定和性质，勾股定理，三角形的中位线定理等知识，正确作出辅助线，证出AG＝MG是解决问题的关键．
13．7
【分析】过点B作BD⊥直线x=6，交直线x=6于点D，过点B作BE⊥x轴，交x轴于点E．则由于四边形OABC是平行四边形，所以OA=BC，又由平行四边形的性质可推得∠OAF=∠BCD，则可证明△OAF≌△BCD，所以OE的长固定不变，当BE最小时，OB取得最小值，即可得出答案．
【详解】解：过点B作BD⊥直线x=6，交直线x=6于点D，过点B作BE⊥x轴，交x轴于点E，直线x=1与OC交于点M，与x轴交于点F，
直线x=6与AB交于点N，如图：
∵四边形OABC是平行四边形，
∴∠OAB=∠BCO，OCAB，OA=BC，
∵直线x=1与直线x=6均垂直于x轴，
∴AMCN，
∴四边形ANCM是平行四边形，
∴∠MAN=∠NCM，
∴∠OAF=∠BCD，
∵∠OFA=∠BDC=90°，
∴∠FOA=∠DBC，
在△OAF和△BCD中，
，
∴△OAF≌△BCD（ASA）．
∴BD=OF=1，
∴OE=6+1=7，
∴
∵OE的长不变，
∴当BE最小时（即B点在x轴上），OB取得最小值，最小值为OB=OE=7．
故答案为7．
【点睛】本题考查了平行四边形的性质、坐标与图形性质、全等三角形的判定与性质，勾股定理；熟练掌握平行四边形的性质，勾股定理，证明三角形全等是解决问题的关键．
14．
【分析】单独一个个求扇形的面积是不可能的，由于所有扇形的圆心角的和正好是多边形的外角和，而多边形的外角和为360°，因此所有扇形正好组成一个半径1的圆．
【详解】观察图形，可知所有扇形的圆心角的和正好是多边形的外角和，即360°.
∵所有扇形正好组成一个半径1的圆.
∴图中阴影部分的面积==.
故答案为:π
【点睛】本题考查多边形的外角和和圆的面积.发现阴影部分的规律是解题的关键.
15．100
【详解】如图，
根据多边形外角和定理得到：∠1+∠2+∠3+∠4+∠5=360°，
∴∠5=360-4×70=80°，
∴∠AED=180-∠5=180-80=100°．
16． 平行四边形 一组对边平行且相等的四边形是平行四边形
【详解】试题解析：四边形BCFE是平行四边形．
理由：∵四边形AEFD是平行四边形，∴AD∥EF，AD=EF．
∵四边形ABCD是平行四边形，∴AD∥BC，AD=BC．
∴EF∥BC，EF=BC，∴四边形BCFE是平行四边形．
故答案为(1). 平行四边形 (2). 一组对边平行且相等的四边形是平行四边形.
17．/0.75
【分析】本题考查了三角形的中位线定理，平行四边形的判定与性质，掌握三角形的中位线定理是解题的关键．
由三角形的中位线定理得到，继而四边形均为平行四边形，则，即可求解．
【详解】解：∵D、E、F分别是的中点，
∴，
∴四边形均为平行四边形，
∴，
∴，
故答案为：．
18．见解析.
【分析】在Rt△MON中，用勾股定理列方程求出x的长，则可得到PM，ON，MN，OP的长，从而证明四边形OPMN是平行四边形.
【详解】解：∵OM⊥ON，∴在直角三角形MON中，OM2+ON2=MN2，
∵OM=4，ON=x-5，MN=5，∴42+（x-5）2=52，解得：x=8，
∴MP=11-x=11-8=3，ON=x-5=8-5=3，OP=x-3=8-3=5，
∴MP=ON，PO=NM，
∴四边形OPMN是平行四边形．
19．(1)点A的坐标为
(2)见解析
(3)
【分析】（1）根据二次根式的性质：被开方数一定大于等于0，去列出不等式组并求解，即可求出点A的坐标；
（2）利用对称的性质、等腰三角形等边对等角的性质和三角形内角和定理，就可得出NC和AP垂直，再得出两组对边分别平行证出平行四边形，由平行四边形性质即可得出求证；
（3）利用勾股定理和直角三角形斜边中线的性质求出和的长，再利用三角形三边关系得出当P、Q、E三点共线时PE的长度最大，进而求出答案．
【详解】（1）解：由二次根式的性质，
可得：m－10≥0且20－2m≥1，
解得m＝10，
当m＝10时，
，
解得n＝6，
故点A的坐标为，
（2）如图，连接NC，
∵△CMO与△NMO关于MO所在直线对称，
∴MO⊥NC，
∴CM＝MN，
∴∠MCN＝∠MNC，
又M为AC中点，
∴AM＝CM，
∴AM＝MN，
∴∠MAN＝∠MNA，
又在△ACN中，
∠ACN＋∠CAN＋∠ANC＝∠ACN＋∠CAN＋∠ANM＋∠MNC＝180°，
即2∠MNC＋2∠ANM＝180°，
∴∠ANC＝∠MNC＋∠ANM＝90°，
即NC⊥AP，
∴MO∥AP
又AM∥OP，
∴四边形MOPA为平行四边形，
∴，
∴点P为OB的中点；
（3）如图，连接OD，取OD的中点Q，
连接EQ、PQ．
由（2）知，点P坐标为
∵CD＝8，OC＝6，
∴，
∴点Q的坐标为，
则，
又∵∠OED＝90°，
∴，
三角形两边之和大于第三边，
即，
∴当P、Q、E三点共线时，
，
此时PE的长度最大，
则PE的最大值．
【点睛】本题主要考查了二次根式的性质、对称图形的性质、平行四边形的判定与性质、勾股定理和三角形三边关系等知识点，牢固掌握以上知识点并能综合应用是做出本题的关键．
20．（1）点B的坐标为；（2）直线的解析式为.
【分析】（1）由正方形的性质可以得到对角线之间的关系，进而得到坐标；
（2）已知两点坐标，用待定系数法求直线解析式.
【详解】解：（1）如图，连接，过点B作轴，点E为垂足，
∵四边形是正方形，
∴，，
故点B的坐标为；
（2）设直线的解析式为，
则，解得．
故直线的解析式为．
【点睛】本题考查了正方形的性质、坐标的表示、待定系数法求一次函数解析式，难度不大.
21．2880°
【分析】首先根据外角和与外角的度数可得多边形的边数，再根据多边形内角和公式计算出答案.
【详解】解：∵多边形的每一个外角都等于20°，
∴它的边数为：360°÷20°=18，
∴它的内角和：180°（18-2）=2880°
故这个多边形的内角和是：2880°.
【点睛】本题主要考查了多边形的内角与外角，关键是正确计算出多边形的边数.
22．(1)；
(2)① 证明见解析；②，证明见解析
【分析】（1）过作于，可求出以及的长，根据，可求出的长度，由即可求出的长；
（2）①有，根据对称有，，可以代换为：，即：，可得，，，可证得：；
②过点E作，当时，可证明，从而可得，由此可得．
【详解】（1）解：如图：过作于，

∵，，
∴
∴，，
∵，
∴，
∴，
∴，
故答案为：．
（2）解：①由对称性质可知：，
∵，
∴，即：，
∴，，
∵，
∴，
∴；
②过点E作，

由①得，
又∵，
∴是等边三角形，
∴，
由①得，
∴四边形是平行四边形，
∴，，
当时，即，
∴，
∴
∴
∴，
∵，
∴，
∴如果，那么，
∴k的值可以是．
【点睛】本题考查了轴对称的性质、直角三角形的性质，等边三角形判定和性质、全等三角形的判定和性质等知识．解题关键是构造全等三角形得，通过转化线段关系得出结论．
23．(1)，菱形
(2)见解析
【分析】本题考查菱形的判定，掌握菱形的判定方法，是解题的关键：
（1）根据题意，补全已知和求证即可；
（2）根据平行四边形的性质结合角平分线的性质，推出，即可得证．
【详解】（1）解：补全已知和求证如下：
已知：如图，在平行四边形中，连接，平分．求证：四边形是菱形；
故答案为：，菱形；
（2）∵平行四边形，
∴，
∴，
∵平分，
∴，
∴，
∴，
∴平行四边形是菱形．
24．（1）四边形为平行四边形．证明见解析；（2）当满足时，四边形是矩形．理由见解析.
【分析】(1)根据一组对边平行且相等的四边形为平行四边形解答即可;(2) 当AB=AC时，四边形AFBD是矩形．先证明，再证明∠ADB=90°即可．
【详解】解：（1）四边形为平行四边形．
证明：∵，，
∴四边形为平行四边形．
（2）当满足时，四边形是矩形．理由如下：
∵，
∴，．
∵为的中点，∴，
∴，
∴．
∵，
∴．
又∵，
∴，即．
∴四边形是矩形．
【点睛】本题考查了全等三角形的判定与性质，以及矩形的判定，熟练掌握全等三角形的判定与性质是解本题的关键．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)