19.3坐标与图形的位置同步练习(含解析)
文档属性
| 名称 | 19.3坐标与图形的位置同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 21:22:21 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
19.3坐标与图形的位置
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.“猫在老鼠南偏西方向50米处”与这句话对应的是( )
A. B.
C. D.
2.某同学的座位号为,那么该同学所坐的位置是( )
A.第2排第4列 B.第4排第2列 C.第6排第2列 D.无法确定
3.数经历了从自然数到有理数,到实数,再到复数的发展过程,数学中把形如a+bi(a,b为实数)的数叫做复数,用z=a+bi表示,任何一个复数z=a+bi在平面直角坐标系中都可以用有序数对Z(a,b)表示,如:z=1+2i表示为Z(1,2),则z=2﹣i可表示为( )
A.Z(2,0) B.Z(2,﹣1) C.Z(2,1) D.Z(﹣1,2)
4.如图,这是小明学校周边环境的示意图,以学校为参照点,儿童公园、图书市场分别距离学校500m,700m,农贸市场距儿童乐园800m,若以(南偏西,500)来表示儿童公园的位置,下列位置表示正确的是( )
A.农贸市场(南偏西,800) B.图书市场(700,南偏东)
C.农贸市场(西偏南,1300) D.图书市场(北偏东,700)
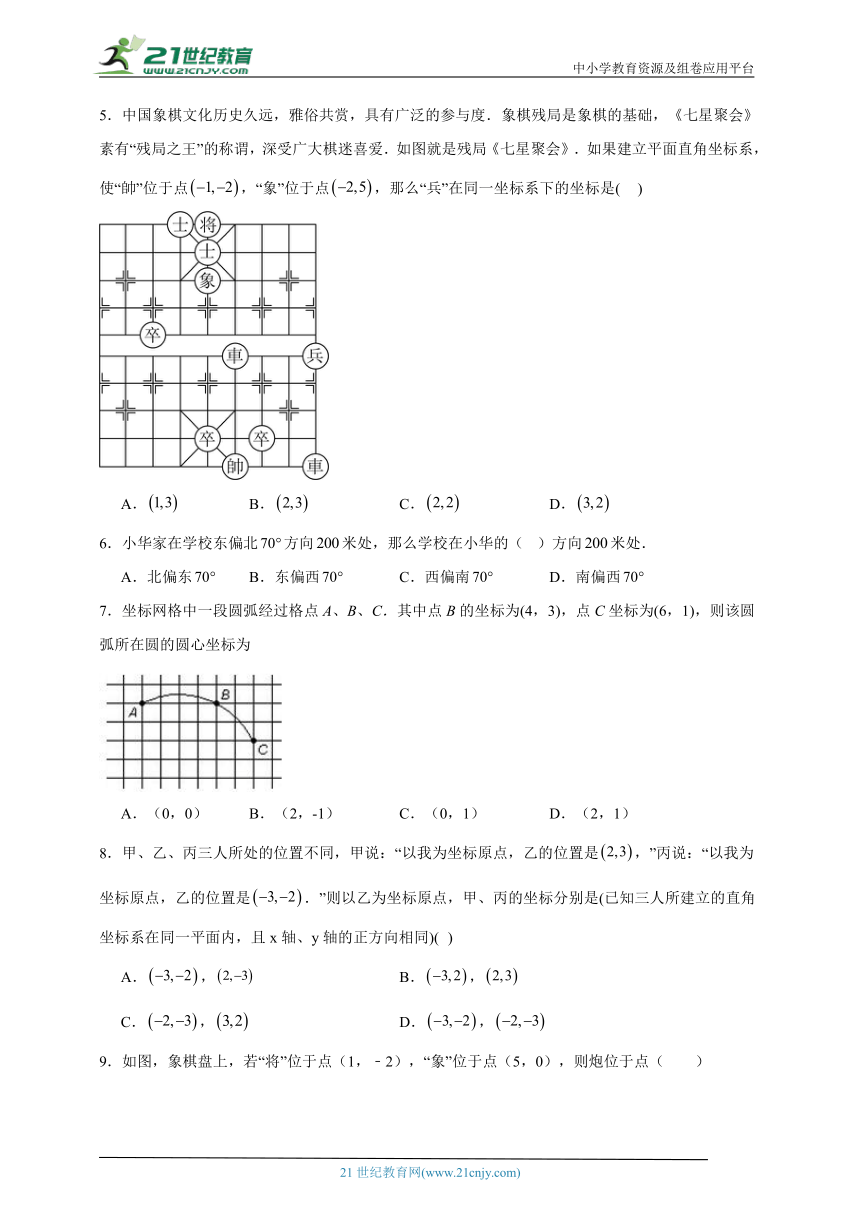
5.中国象棋文化历史久远,雅俗共赏,具有广泛的参与度.象棋残局是象棋的基础,《七星聚会》素有“残局之王”的称谓,深受广大棋迷喜爱.如图就是残局《七星聚会》.如果建立平面直角坐标系,使“帥”位于点,“象”位于点,那么“兵”在同一坐标系下的坐标是( )
A. B. C. D.
6.小华家在学校东偏北方向米处,那么学校在小华的( )方向米处.
A.北偏东 B.东偏西 C.西偏南 D.南偏西
7.坐标网格中一段圆弧经过格点A、B、C.其中点B的坐标为(4,3),点C坐标为(6,1),则该圆弧所在圆的圆心坐标为
A.(0,0) B.(2,-1) C.(0,1) D.(2,1)
8.甲、乙、丙三人所处的位置不同,甲说:“以我为坐标原点,乙的位置是,”丙说:“以我为坐标原点,乙的位置是.”则以乙为坐标原点,甲、丙的坐标分别是(已知三人所建立的直角坐标系在同一平面内,且x轴、y轴的正方向相同)( )
A., B.,
C., D.,
9.如图,象棋盘上,若“将”位于点(1,﹣2),“象”位于点(5,0),则炮位于点( )
A.(﹣1,1) B.(﹣1,2) C.(﹣2,1) D.(﹣2,2)
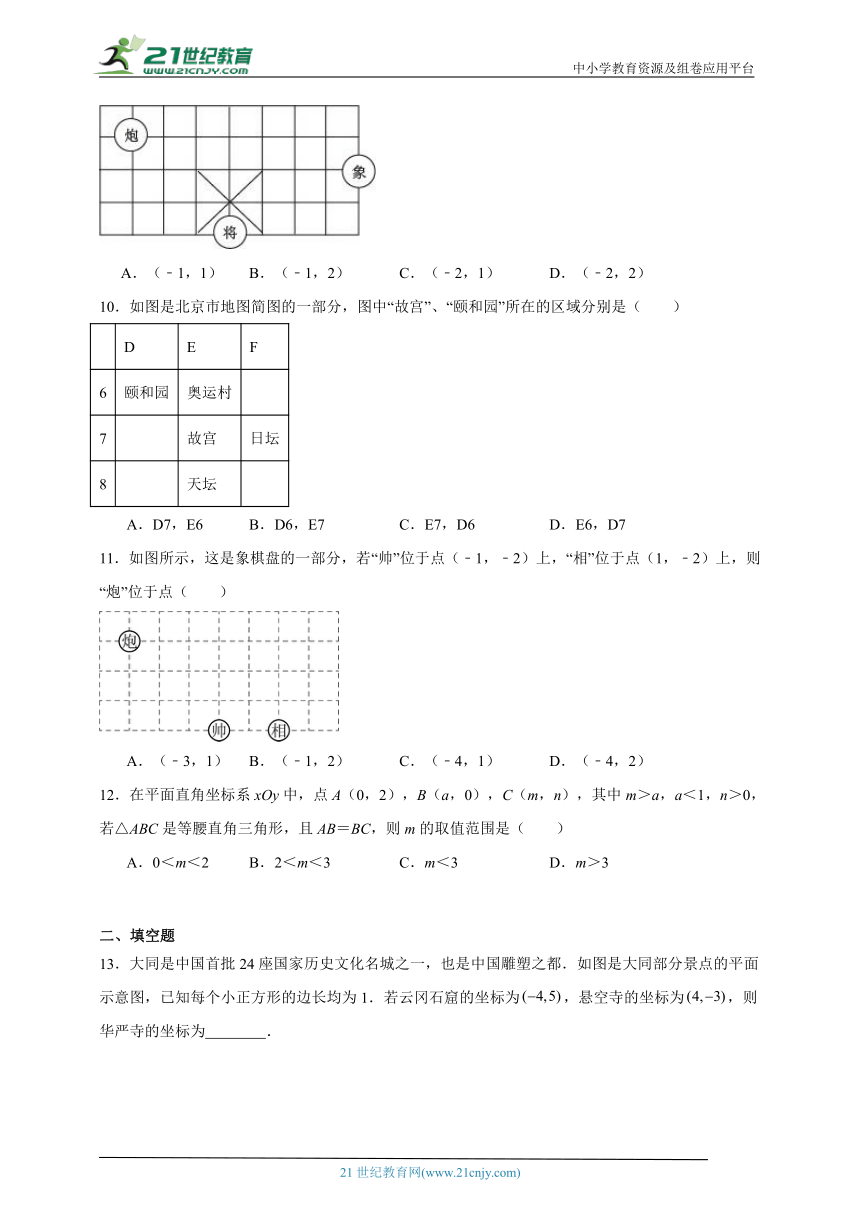
10.如图是北京市地图简图的一部分,图中“故宫”、“颐和园”所在的区域分别是( )
D E F
6 颐和园 奥运村
7 故宫 日坛
8 天坛
A.D7,E6 B.D6,E7 C.E7,D6 D.E6,D7
11.如图所示,这是象棋盘的一部分,若“帅”位于点(﹣1,﹣2)上,“相”位于点(1,﹣2)上,则“炮”位于点( )
A.(﹣3,1) B.(﹣1,2) C.(﹣4,1) D.(﹣4,2)
12.在平面直角坐标系xOy中,点A(0,2),B(a,0),C(m,n),其中m>a,a<1,n>0,若△ABC是等腰直角三角形,且AB=BC,则m的取值范围是( )
A.0<m<2 B.2<m<3 C.m<3 D.m>3
二、填空题
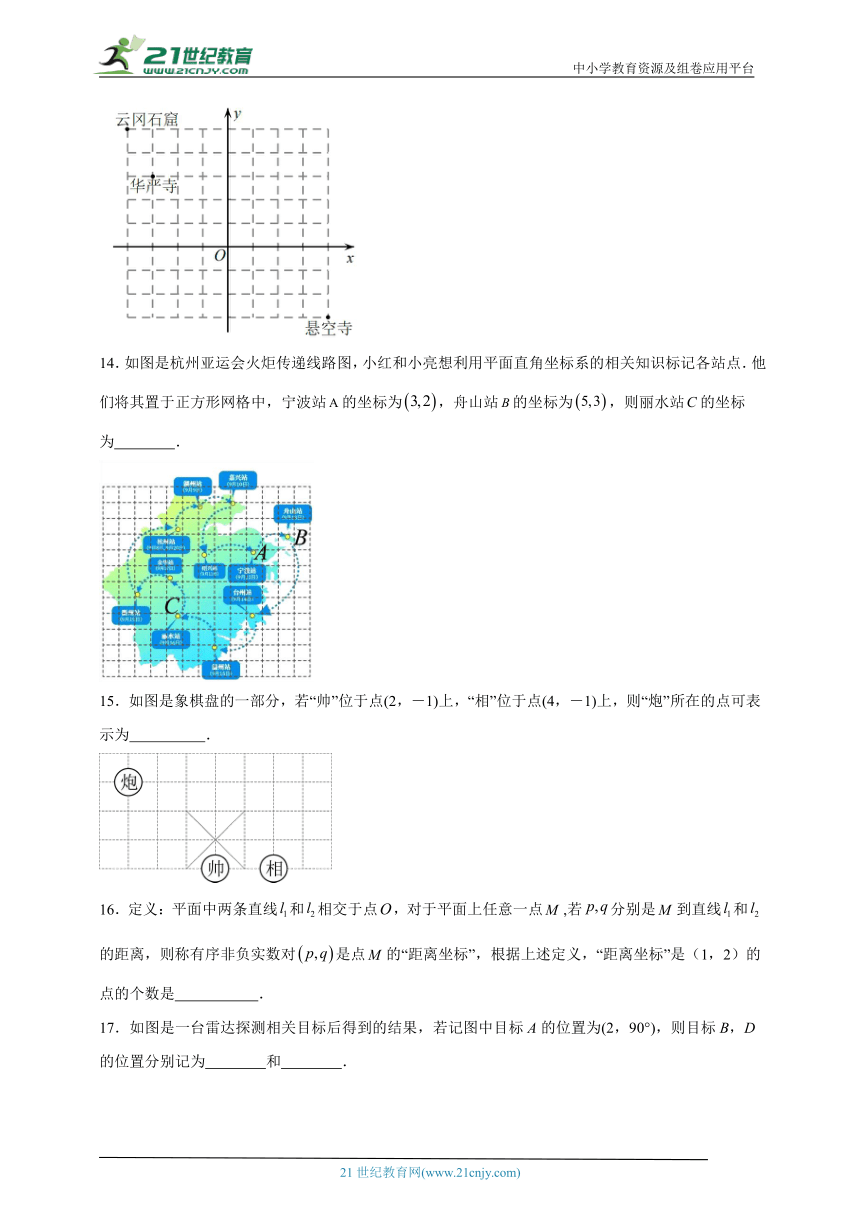
13.大同是中国首批24座国家历史文化名城之一,也是中国雕塑之都.如图是大同部分景点的平面示意图,已知每个小正方形的边长均为1.若云冈石窟的坐标为,悬空寺的坐标为,则华严寺的坐标为 .
14.如图是杭州亚运会火炬传递线路图,小红和小亮想利用平面直角坐标系的相关知识标记各站点.他们将其置于正方形网格中,宁波站的坐标为,舟山站的坐标为,则丽水站的坐标为 .
15.如图是象棋盘的一部分,若“帅”位于点(2,-1)上,“相”位于点(4,-1)上,则“炮”所在的点可表示为 .
16.定义:平面中两条直线和相交于点,对于平面上任意一点,若分别是到直线和的距离,则称有序非负实数对是点的“距离坐标”,根据上述定义,“距离坐标”是(1,2)的点的个数是 .
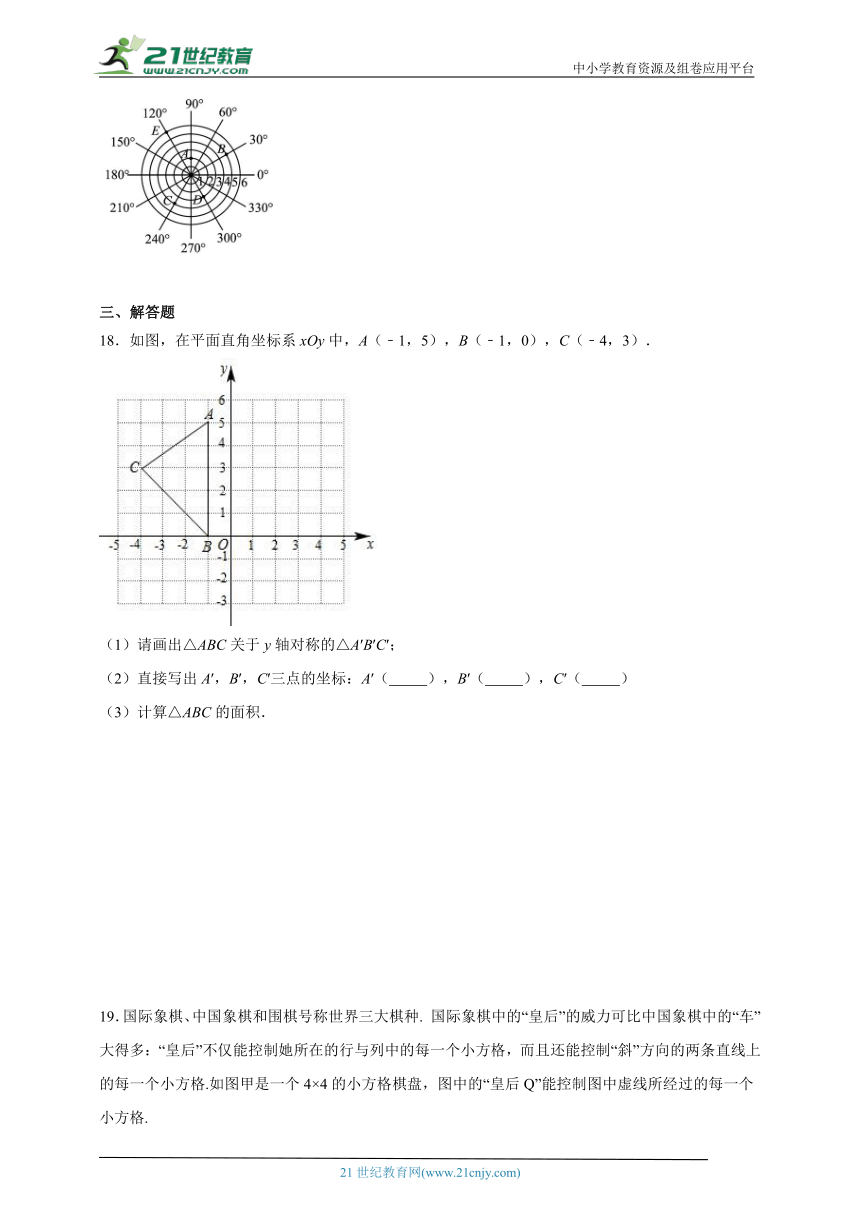
17.如图是一台雷达探测相关目标后得到的结果,若记图中目标A的位置为(2,90°),则目标B,D的位置分别记为 和 .
三、解答题
18.如图,在平面直角坐标系xOy中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)请画出△ABC关于y轴对称的△A′B′C′;
(2)直接写出A′,B′,C′三点的坐标:A′( ),B′( ),C′( )
(3)计算△ABC的面积.
19.国际象棋、中国象棋和围棋号称世界三大棋种. 国际象棋中的“皇后”的威力可比中国象棋中的“车”大得多:“皇后”不仅能控制她所在的行与列中的每一个小方格,而且还能控制“斜”方向的两条直线上的每一个小方格.如图甲是一个4×4的小方格棋盘,图中的“皇后Q”能控制图中虚线所经过的每一个小方格.
(1)在如图乙的小方格棋盘中有一“皇后Q”,她所在的位置可用“(2,3)”来表示,请说明“皇后Q”所在的位置“(2,3)”的意义,并用这种表示法分别写出棋盘中不能被该“皇后Q”所控制的四个位置.
(2)如图丙也是一个4×4的小方格棋盘,请在这个棋盘中放入四个“皇后Q”,使这四个“皇后Q”之间互不受对方控制(在图丙中的某四个小方格中标出字母Q即可).
20.如图,小正方形的边长为1,已知鹰嘴崖坐标为,先建立平面直角坐标系,再表示各景点的坐标.
21.小强放学后,先向东走了300米,再向北走路200米,到书店A买了一本书,然后向西走了500米,再向南走了100米,到快餐店B买了零食,又向南走了400米,再向东走了800米,回到他家C,如图,以学校为原点建立坐标系,图中的每个单位长度表示100米.
(1)请在图中的坐标系中标出A,B,C的位置,并写出A,B,C三点的坐标;
(2)如果超市D的坐标为(-1,-3),邮局E的坐标为(4,2),请在图中标出超市和邮局的位置;
(3)请求出小强家到超市的实际距离.
22.如图所示为某市几个旅游景点分布示意图(图中每个小正方形的边长均为1个单位),如果用(0,0)表示公园,用(2,2)表示西湖.
(1)图中风云堂、碧水池的位置如何表示?
(2)用距离和方向角表示风云堂相对于西湖的位置.
23.如图,这是某学校的平面示意图,图中小方格都是边长为1个单位长度的正方形,若艺术楼的坐标为,实验楼的坐标为.
(1)a= ,b= .
(2)请在图中画出平面直角坐标系xOy,并写出教学楼与体育馆的坐标.
24.如图中标明了小英家附近的一些地方,以小英家为坐标原点建立如图所示的坐标系.
(1)写出汽车站和消防站的坐标;
(2)某星期日早晨,小英同学从家里出发,沿,,,,,的路线转了一下,又回到家里,写出路上她经过的地方.
《19.3坐标与图形的位置》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A D B D C C B C C C
题号 11 12
答案 C B
1.A
【分析】本题考查的是利用方向角与距离表示物体的位置,理解方向角的含义是解本题的关键.根据上北下南,左西右东,确定方向,再根据方向角与距离确定位置即可.
【详解】解:“猫在老鼠南偏西方向50米处”对应的图形是:
故选:A.
2.D
【分析】实际生活中的有序数对是有实际意义的,没有交待清楚,所以不好确定.
【详解】解:已知座位号为,但从题中无法获知“2”和“4”分别表示什么,故无法确定该同学的位置.
故选:D.
【点睛】本题考查确定物体的位置,理解有序数对的两个数的实际意义是解题的关键.
3.B
【分析】根据题中的新定义解答即可.
【详解】解:由题意,得z=2 i可表示为Z(2, 1).
故选:B.
【点睛】本题考查了点的坐标,弄清题中的新定义是解本题的关键.
4.D
【分析】根据方向角的概念,仿照表示儿童公园的位置的方法,即可解答.
【详解】解:由图可知:农贸市场(南偏西,1300);图书市场(北偏东,700);
故选D
【点睛】本题考查了方向角,根据题目的已知条件并结合图形分析是解题的关键.
5.C
【分析】根据“帥”和“象”的坐标建立正确的坐标系即可得到答案.
【详解】解:由题意可建立如下平面直角坐标系,
∴“兵”的坐标是,
故选:C.
【点睛】本题主要考查了坐标的实际应用,正确建立坐标系是解题的关键.
6.C
【分析】本题考查了位置与方向,解题的关键是掌握相对位置的概念.东西相对,南北相对,交换两个位置作观测点,把方向与相对方向交换,角度不变,距离不变,即可求解.
【详解】解:小华家在学校东偏北方向米处,那么学校在小华的西偏南方向米处,
故选:C.
7.B
【分析】根据已知点的坐标画出平面直角坐标系,根据三点确定一个圆的方法画出圆心位置.
【详解】如图,根据已知点的坐标画出平面直角坐标系,连接BC,线段AB的垂直平分线EF交BC的垂直平分线于Q,则Q为圆弧的圆心,
∴圆心的坐标是
故选B.
【点睛】本题考查三点确定一个圆的作法(用两条弦的垂直平分线确定圆心位置),结合平面直角坐标系写出圆心的位置,解题的关键是画出平面直角坐标系,找出圆心位置.
8.C
【分析】由于已知三人建立坐标时,x轴y轴正方向相同,以甲为坐标原点,乙的位置是(2,3),则以乙为坐标原点,甲的位置是(-2,-3);同样,以乙为坐标原点,丙的位置是(3,2).
【详解】∵以甲为坐标原点,乙的位置是,
∴以乙为坐标原点,甲的位置是;
∵以丙为坐标原点,乙的位置是,
∴以乙为坐标原点,丙的位置是.
故选C.
【点睛】本题考查了坐标确定位置:直角坐标平面内点的位置由有序实数对确定,有序实数对与点一一对应.
9.C
【分析】根据“将”的位置向左平移一个单位所得直线是y轴,向上平移2个单位所得直线是x轴,根据“炮”的位置,可得答案.
【详解】解:根据题意可建立如图所示坐标系,
由坐标系知炮位于点(﹣2,1),
故选C.
【点睛】本题考查了坐标确定位置,利用“将”的位置向左平移一个单位所得直线是y轴,向上平移2个单位所得直线是x轴是解题关键.
10.C
【分析】直接利用已知网格得出“故宫”、“颐和园”所在位置.
【详解】如图所示:图中“故宫”、“颐和园”所在的区域分别是:E7,D6.
故选:C.
【点睛】此题主要考查了坐标确定位置,正确理解位置的意义是解题关键.
11.C
【分析】以帅向左一个单位,向上两个单位为坐标原点建立平面直角坐标系,然后写出炮的坐标即可.
【详解】解:建立平面直角坐标系如图所示,
炮位于点(﹣4,1).
故选:C.
【点睛】本题考查了坐标确定位置,准确确定出坐标原点的位置是解题的关键.
12.B
【分析】过点C作CD⊥x轴于D,由“AAS”可证△AOB≌△BDC,可得AO=BD=2,BO=CD=n=a,即可求解.
【详解】解:如图,过点C作CD⊥x轴于D,
∵点A(0,2),
∴AO=2,
∵△ABC是等腰直角三角形,且AB=BC,
∴∠ABC=90°=∠AOB=∠BDC,
∴∠ABO+∠CBD=90°
∠ABO+∠BAO=90°,
∴∠BAO=∠CBD,
在△AOB和△BDC中,
,
∴△AOB≌△BDC(AAS),
∴AO=BD=2,BO=CD=n=a,
∴0<a<1,
∵OD=OB+BD=2+a=m,
∴2<m<3,
故选:B.
【点睛】本题考查了等腰直角三角形的性质、全等三角形的性质与判定、不等式和坐标等知识,解题关键是树立数形结合思想,把坐标与线段长联系起来,确定取值范围.
13.
【分析】根据题意建立坐标系,由坐标系可得答案.
【详解】解:建立坐标系如图:
由题意可得华严寺的坐标为,
故答案为:.
【点睛】本题考查直角坐标系,根据题意建立坐标系是解题的关键.
14.
【分析】本题考查了坐标与图形,属于常见题型,先由A、B两点的坐标建立平面直角坐标系是,进而可解题.
【详解】解:由,可建立如图所示的平面直角坐标系:
∴点C的坐标是.
故答案为:.
15.(-1,2)
【详解】解:根据“帅”位于点(2,-1)上,“相”位于点(4,-1)上,可知棋盘中一个格代表一个单位,“炮”所在的点在帅左面3个单位,上面3个单位,故坐标是(-1,2).
故答案为(-1,2).
16.4
【分析】若p,q分别是M到直线l1和l2的距离,则称有序非负实数对(p,q)是点M的“距离坐标”,根据定义,“距离坐标”是(1,2)的点,说明M到直线l1和l2的距离分别是1和2,这样的点在平面被直线l1和l2的四个区域,各有一个点,即可求出答案.
【详解】解:因为平面中两条直线l1和l2相交于点O,对于平面上任意一点M,
若p,q分别是M到直线l1和l2的距离,
则称有序非负实数对(p,q)是点M的“距离坐标”,
根据上述定义,“距离坐标”是(1,2)的点可以在两条直线相交所成的四个区域内各找到1个,
所以满足条件的点的个数是4个.
故答案为:4.
【点睛】此题考查了坐标确定位置;解题的关键是要注意两条直线相交时有四个区域,本题是一个好题目,有创新性,但是难度较小,理解题意不难解答,考查学生的逻辑思维能力.
17. (5,30°) (3,300°)
【分析】根据坐标的第一个数表示到中心的距离,第二个数表示角度,分别写出各目标的坐标即可.
【详解】解:B(5,30°) ,D(3,300°).
故答案为(5,30°),(3,300°).
【点睛】本题考查坐标确定位置,坐标与图形的性质,理解题目中表示位置的两个数的实际意义是解题的关键.
18.(1)见解析;(2)A′(1,5),B′(1,0),C′(4,3);(3)7.5
【分析】(1)根据网格结构找出点A、B、C的对应点A′、B′、C′的位置,然后顺次连接即可;
(2)根据平面直角坐标系写出点的坐标即可;
(3)利用三角形的面积公式列式进行计算即可求解.
【详解】解:(1)如图所示
(2)A′( 1,5 ),B′( 1,0 ),C′( 4,3 )
(3)∵A(﹣1,5),B(﹣1,0),C(﹣4,3),
∴AB=5,AB边上的高为3,∴S△ABC=.
【点睛】本题考查了利用轴对称变换作图,熟悉网格结构并找出对应点的位置是解题的关键.
19.见解析.
【详解】试题分析:仔细阅读题意,正确理解“皇后”的控制范围即可得到结果.
(1)“皇后Q”所在的位置(2,3)表示“皇后Q”位于第2列第3行,棋盘中不能被该“皇后Q”所控制的四个位置是(1,1)、(3,1)、(4,2)、(4,4);
(2)(1.3)、(2,1)、(3,4)、(4,2)或(1,2)、(2,4)、(3,1)、(4,3).
考点:坐标与图形性质
点评:解答本题的关键是读懂题意,正确理解“皇后”的控制范围,再应用于解题.
20.图见解析,驼峰,马山,一线天,象脚山,掉魂桥
【分析】此题主要考查了坐标确定位置,先根据鹰嘴崖坐标为画出平面直角坐标系,再依次写出各景点的坐标即可.关键是正确确定坐标系原点位置.
【详解】解:建立平面直角坐标系如图所示:
驼峰,马山,一线天,象脚山,掉魂桥.
21.(1)A(3,2),B(-2,1),C(6,-3)(2)见解析(3)700
【分析】(1)利用小强所走路线可在坐标系中可标出A,B,C的位置,然后根据各象限点的坐标特征写出A,B,C三点的坐标;
(2)利用D和E点坐标标出超市和邮局的位置;
(3)求出CD的长即可得到小强家到超市的实际距离.
【详解】(1)如图,A(3,2),B(﹣2,1),C(6,﹣3);
(2)如图;
(3)CD=700,所以小强家到超市的实际距离为700m.
【点睛】本题考查了坐标确定位置:平面内的点与有序实数对一一对应;记住直角坐标系中特殊位置点的坐标特征.
22.(1)风云堂表示为(5,5),碧水池表示为(6,1).(2)风云堂位于西湖的北偏东45°方向且距西湖3个单位处.
【分析】先画出直角坐标系,然后利用方格图写出各景点的坐标和距离和方向角表示出风云堂相对于西湖的位置.
【详解】解:如图,
(1)风云堂表示为(5,5),碧水池表示为(6,1).(2)风云堂位于西湖的北偏东45°方向且距西湖3个单位处.
【点睛】本题考查坐标确定位置:直角坐标平面内点的位置由有序实数对确定,有序实数对与点一一对应.
23.(1)1,
(2)图见解析;教学楼坐标为,体育馆的坐标为
【分析】(1)根据已知点坐标得到原点位置,进而作出平面直角坐标系,即可得出答案;
(2)根据(1)中平面直角坐标系可得答案.
【详解】(1)解:根据题意,画出直角直角坐标系如图:
由图知,艺术楼的坐标为,实验楼的坐标为,
∴,.
故答案为:1,;
(2)解:平面直角坐标系如上图所示;
由图可知,教学楼坐标为,体育馆的坐标为.
【点睛】本题考查坐标确定位置,正确得到原点位置并画出平面直角坐标系是解答的关键.
24.(1)汽车站(1,1),消防站(2,﹣2);(2)(2)小英经过的地方:游乐场,公园,姥姥家,宠物店,邮局.
【分析】(1)根据平面直角坐标系直接写出坐标即可;(2)根据平面直角坐标系找出各点对应的位置,然后写出经过的地方.
【详解】(1)汽车站(1,1),消防站(2,﹣2);
(2)小英经过的地方:游乐场,公园,姥姥家,宠物店,邮局.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
19.3坐标与图形的位置
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.“猫在老鼠南偏西方向50米处”与这句话对应的是( )
A. B.
C. D.
2.某同学的座位号为,那么该同学所坐的位置是( )
A.第2排第4列 B.第4排第2列 C.第6排第2列 D.无法确定
3.数经历了从自然数到有理数,到实数,再到复数的发展过程,数学中把形如a+bi(a,b为实数)的数叫做复数,用z=a+bi表示,任何一个复数z=a+bi在平面直角坐标系中都可以用有序数对Z(a,b)表示,如:z=1+2i表示为Z(1,2),则z=2﹣i可表示为( )
A.Z(2,0) B.Z(2,﹣1) C.Z(2,1) D.Z(﹣1,2)
4.如图,这是小明学校周边环境的示意图,以学校为参照点,儿童公园、图书市场分别距离学校500m,700m,农贸市场距儿童乐园800m,若以(南偏西,500)来表示儿童公园的位置,下列位置表示正确的是( )
A.农贸市场(南偏西,800) B.图书市场(700,南偏东)
C.农贸市场(西偏南,1300) D.图书市场(北偏东,700)
5.中国象棋文化历史久远,雅俗共赏,具有广泛的参与度.象棋残局是象棋的基础,《七星聚会》素有“残局之王”的称谓,深受广大棋迷喜爱.如图就是残局《七星聚会》.如果建立平面直角坐标系,使“帥”位于点,“象”位于点,那么“兵”在同一坐标系下的坐标是( )
A. B. C. D.
6.小华家在学校东偏北方向米处,那么学校在小华的( )方向米处.
A.北偏东 B.东偏西 C.西偏南 D.南偏西
7.坐标网格中一段圆弧经过格点A、B、C.其中点B的坐标为(4,3),点C坐标为(6,1),则该圆弧所在圆的圆心坐标为
A.(0,0) B.(2,-1) C.(0,1) D.(2,1)
8.甲、乙、丙三人所处的位置不同,甲说:“以我为坐标原点,乙的位置是,”丙说:“以我为坐标原点,乙的位置是.”则以乙为坐标原点,甲、丙的坐标分别是(已知三人所建立的直角坐标系在同一平面内,且x轴、y轴的正方向相同)( )
A., B.,
C., D.,
9.如图,象棋盘上,若“将”位于点(1,﹣2),“象”位于点(5,0),则炮位于点( )
A.(﹣1,1) B.(﹣1,2) C.(﹣2,1) D.(﹣2,2)
10.如图是北京市地图简图的一部分,图中“故宫”、“颐和园”所在的区域分别是( )
D E F
6 颐和园 奥运村
7 故宫 日坛
8 天坛
A.D7,E6 B.D6,E7 C.E7,D6 D.E6,D7
11.如图所示,这是象棋盘的一部分,若“帅”位于点(﹣1,﹣2)上,“相”位于点(1,﹣2)上,则“炮”位于点( )
A.(﹣3,1) B.(﹣1,2) C.(﹣4,1) D.(﹣4,2)
12.在平面直角坐标系xOy中,点A(0,2),B(a,0),C(m,n),其中m>a,a<1,n>0,若△ABC是等腰直角三角形,且AB=BC,则m的取值范围是( )
A.0<m<2 B.2<m<3 C.m<3 D.m>3
二、填空题
13.大同是中国首批24座国家历史文化名城之一,也是中国雕塑之都.如图是大同部分景点的平面示意图,已知每个小正方形的边长均为1.若云冈石窟的坐标为,悬空寺的坐标为,则华严寺的坐标为 .
14.如图是杭州亚运会火炬传递线路图,小红和小亮想利用平面直角坐标系的相关知识标记各站点.他们将其置于正方形网格中,宁波站的坐标为,舟山站的坐标为,则丽水站的坐标为 .
15.如图是象棋盘的一部分,若“帅”位于点(2,-1)上,“相”位于点(4,-1)上,则“炮”所在的点可表示为 .
16.定义:平面中两条直线和相交于点,对于平面上任意一点,若分别是到直线和的距离,则称有序非负实数对是点的“距离坐标”,根据上述定义,“距离坐标”是(1,2)的点的个数是 .
17.如图是一台雷达探测相关目标后得到的结果,若记图中目标A的位置为(2,90°),则目标B,D的位置分别记为 和 .
三、解答题
18.如图,在平面直角坐标系xOy中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)请画出△ABC关于y轴对称的△A′B′C′;
(2)直接写出A′,B′,C′三点的坐标:A′( ),B′( ),C′( )
(3)计算△ABC的面积.
19.国际象棋、中国象棋和围棋号称世界三大棋种. 国际象棋中的“皇后”的威力可比中国象棋中的“车”大得多:“皇后”不仅能控制她所在的行与列中的每一个小方格,而且还能控制“斜”方向的两条直线上的每一个小方格.如图甲是一个4×4的小方格棋盘,图中的“皇后Q”能控制图中虚线所经过的每一个小方格.
(1)在如图乙的小方格棋盘中有一“皇后Q”,她所在的位置可用“(2,3)”来表示,请说明“皇后Q”所在的位置“(2,3)”的意义,并用这种表示法分别写出棋盘中不能被该“皇后Q”所控制的四个位置.
(2)如图丙也是一个4×4的小方格棋盘,请在这个棋盘中放入四个“皇后Q”,使这四个“皇后Q”之间互不受对方控制(在图丙中的某四个小方格中标出字母Q即可).
20.如图,小正方形的边长为1,已知鹰嘴崖坐标为,先建立平面直角坐标系,再表示各景点的坐标.
21.小强放学后,先向东走了300米,再向北走路200米,到书店A买了一本书,然后向西走了500米,再向南走了100米,到快餐店B买了零食,又向南走了400米,再向东走了800米,回到他家C,如图,以学校为原点建立坐标系,图中的每个单位长度表示100米.
(1)请在图中的坐标系中标出A,B,C的位置,并写出A,B,C三点的坐标;
(2)如果超市D的坐标为(-1,-3),邮局E的坐标为(4,2),请在图中标出超市和邮局的位置;
(3)请求出小强家到超市的实际距离.
22.如图所示为某市几个旅游景点分布示意图(图中每个小正方形的边长均为1个单位),如果用(0,0)表示公园,用(2,2)表示西湖.
(1)图中风云堂、碧水池的位置如何表示?
(2)用距离和方向角表示风云堂相对于西湖的位置.
23.如图,这是某学校的平面示意图,图中小方格都是边长为1个单位长度的正方形,若艺术楼的坐标为,实验楼的坐标为.
(1)a= ,b= .
(2)请在图中画出平面直角坐标系xOy,并写出教学楼与体育馆的坐标.
24.如图中标明了小英家附近的一些地方,以小英家为坐标原点建立如图所示的坐标系.
(1)写出汽车站和消防站的坐标;
(2)某星期日早晨,小英同学从家里出发,沿,,,,,的路线转了一下,又回到家里,写出路上她经过的地方.
《19.3坐标与图形的位置》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A D B D C C B C C C
题号 11 12
答案 C B
1.A
【分析】本题考查的是利用方向角与距离表示物体的位置,理解方向角的含义是解本题的关键.根据上北下南,左西右东,确定方向,再根据方向角与距离确定位置即可.
【详解】解:“猫在老鼠南偏西方向50米处”对应的图形是:
故选:A.
2.D
【分析】实际生活中的有序数对是有实际意义的,没有交待清楚,所以不好确定.
【详解】解:已知座位号为,但从题中无法获知“2”和“4”分别表示什么,故无法确定该同学的位置.
故选:D.
【点睛】本题考查确定物体的位置,理解有序数对的两个数的实际意义是解题的关键.
3.B
【分析】根据题中的新定义解答即可.
【详解】解:由题意,得z=2 i可表示为Z(2, 1).
故选:B.
【点睛】本题考查了点的坐标,弄清题中的新定义是解本题的关键.
4.D
【分析】根据方向角的概念,仿照表示儿童公园的位置的方法,即可解答.
【详解】解:由图可知:农贸市场(南偏西,1300);图书市场(北偏东,700);
故选D
【点睛】本题考查了方向角,根据题目的已知条件并结合图形分析是解题的关键.
5.C
【分析】根据“帥”和“象”的坐标建立正确的坐标系即可得到答案.
【详解】解:由题意可建立如下平面直角坐标系,
∴“兵”的坐标是,
故选:C.
【点睛】本题主要考查了坐标的实际应用,正确建立坐标系是解题的关键.
6.C
【分析】本题考查了位置与方向,解题的关键是掌握相对位置的概念.东西相对,南北相对,交换两个位置作观测点,把方向与相对方向交换,角度不变,距离不变,即可求解.
【详解】解:小华家在学校东偏北方向米处,那么学校在小华的西偏南方向米处,
故选:C.
7.B
【分析】根据已知点的坐标画出平面直角坐标系,根据三点确定一个圆的方法画出圆心位置.
【详解】如图,根据已知点的坐标画出平面直角坐标系,连接BC,线段AB的垂直平分线EF交BC的垂直平分线于Q,则Q为圆弧的圆心,
∴圆心的坐标是
故选B.
【点睛】本题考查三点确定一个圆的作法(用两条弦的垂直平分线确定圆心位置),结合平面直角坐标系写出圆心的位置,解题的关键是画出平面直角坐标系,找出圆心位置.
8.C
【分析】由于已知三人建立坐标时,x轴y轴正方向相同,以甲为坐标原点,乙的位置是(2,3),则以乙为坐标原点,甲的位置是(-2,-3);同样,以乙为坐标原点,丙的位置是(3,2).
【详解】∵以甲为坐标原点,乙的位置是,
∴以乙为坐标原点,甲的位置是;
∵以丙为坐标原点,乙的位置是,
∴以乙为坐标原点,丙的位置是.
故选C.
【点睛】本题考查了坐标确定位置:直角坐标平面内点的位置由有序实数对确定,有序实数对与点一一对应.
9.C
【分析】根据“将”的位置向左平移一个单位所得直线是y轴,向上平移2个单位所得直线是x轴,根据“炮”的位置,可得答案.
【详解】解:根据题意可建立如图所示坐标系,
由坐标系知炮位于点(﹣2,1),
故选C.
【点睛】本题考查了坐标确定位置,利用“将”的位置向左平移一个单位所得直线是y轴,向上平移2个单位所得直线是x轴是解题关键.
10.C
【分析】直接利用已知网格得出“故宫”、“颐和园”所在位置.
【详解】如图所示:图中“故宫”、“颐和园”所在的区域分别是:E7,D6.
故选:C.
【点睛】此题主要考查了坐标确定位置,正确理解位置的意义是解题关键.
11.C
【分析】以帅向左一个单位,向上两个单位为坐标原点建立平面直角坐标系,然后写出炮的坐标即可.
【详解】解:建立平面直角坐标系如图所示,
炮位于点(﹣4,1).
故选:C.
【点睛】本题考查了坐标确定位置,准确确定出坐标原点的位置是解题的关键.
12.B
【分析】过点C作CD⊥x轴于D,由“AAS”可证△AOB≌△BDC,可得AO=BD=2,BO=CD=n=a,即可求解.
【详解】解:如图,过点C作CD⊥x轴于D,
∵点A(0,2),
∴AO=2,
∵△ABC是等腰直角三角形,且AB=BC,
∴∠ABC=90°=∠AOB=∠BDC,
∴∠ABO+∠CBD=90°
∠ABO+∠BAO=90°,
∴∠BAO=∠CBD,
在△AOB和△BDC中,
,
∴△AOB≌△BDC(AAS),
∴AO=BD=2,BO=CD=n=a,
∴0<a<1,
∵OD=OB+BD=2+a=m,
∴2<m<3,
故选:B.
【点睛】本题考查了等腰直角三角形的性质、全等三角形的性质与判定、不等式和坐标等知识,解题关键是树立数形结合思想,把坐标与线段长联系起来,确定取值范围.
13.
【分析】根据题意建立坐标系,由坐标系可得答案.
【详解】解:建立坐标系如图:
由题意可得华严寺的坐标为,
故答案为:.
【点睛】本题考查直角坐标系,根据题意建立坐标系是解题的关键.
14.
【分析】本题考查了坐标与图形,属于常见题型,先由A、B两点的坐标建立平面直角坐标系是,进而可解题.
【详解】解:由,可建立如图所示的平面直角坐标系:
∴点C的坐标是.
故答案为:.
15.(-1,2)
【详解】解:根据“帅”位于点(2,-1)上,“相”位于点(4,-1)上,可知棋盘中一个格代表一个单位,“炮”所在的点在帅左面3个单位,上面3个单位,故坐标是(-1,2).
故答案为(-1,2).
16.4
【分析】若p,q分别是M到直线l1和l2的距离,则称有序非负实数对(p,q)是点M的“距离坐标”,根据定义,“距离坐标”是(1,2)的点,说明M到直线l1和l2的距离分别是1和2,这样的点在平面被直线l1和l2的四个区域,各有一个点,即可求出答案.
【详解】解:因为平面中两条直线l1和l2相交于点O,对于平面上任意一点M,
若p,q分别是M到直线l1和l2的距离,
则称有序非负实数对(p,q)是点M的“距离坐标”,
根据上述定义,“距离坐标”是(1,2)的点可以在两条直线相交所成的四个区域内各找到1个,
所以满足条件的点的个数是4个.
故答案为:4.
【点睛】此题考查了坐标确定位置;解题的关键是要注意两条直线相交时有四个区域,本题是一个好题目,有创新性,但是难度较小,理解题意不难解答,考查学生的逻辑思维能力.
17. (5,30°) (3,300°)
【分析】根据坐标的第一个数表示到中心的距离,第二个数表示角度,分别写出各目标的坐标即可.
【详解】解:B(5,30°) ,D(3,300°).
故答案为(5,30°),(3,300°).
【点睛】本题考查坐标确定位置,坐标与图形的性质,理解题目中表示位置的两个数的实际意义是解题的关键.
18.(1)见解析;(2)A′(1,5),B′(1,0),C′(4,3);(3)7.5
【分析】(1)根据网格结构找出点A、B、C的对应点A′、B′、C′的位置,然后顺次连接即可;
(2)根据平面直角坐标系写出点的坐标即可;
(3)利用三角形的面积公式列式进行计算即可求解.
【详解】解:(1)如图所示
(2)A′( 1,5 ),B′( 1,0 ),C′( 4,3 )
(3)∵A(﹣1,5),B(﹣1,0),C(﹣4,3),
∴AB=5,AB边上的高为3,∴S△ABC=.
【点睛】本题考查了利用轴对称变换作图,熟悉网格结构并找出对应点的位置是解题的关键.
19.见解析.
【详解】试题分析:仔细阅读题意,正确理解“皇后”的控制范围即可得到结果.
(1)“皇后Q”所在的位置(2,3)表示“皇后Q”位于第2列第3行,棋盘中不能被该“皇后Q”所控制的四个位置是(1,1)、(3,1)、(4,2)、(4,4);
(2)(1.3)、(2,1)、(3,4)、(4,2)或(1,2)、(2,4)、(3,1)、(4,3).
考点:坐标与图形性质
点评:解答本题的关键是读懂题意,正确理解“皇后”的控制范围,再应用于解题.
20.图见解析,驼峰,马山,一线天,象脚山,掉魂桥
【分析】此题主要考查了坐标确定位置,先根据鹰嘴崖坐标为画出平面直角坐标系,再依次写出各景点的坐标即可.关键是正确确定坐标系原点位置.
【详解】解:建立平面直角坐标系如图所示:
驼峰,马山,一线天,象脚山,掉魂桥.
21.(1)A(3,2),B(-2,1),C(6,-3)(2)见解析(3)700
【分析】(1)利用小强所走路线可在坐标系中可标出A,B,C的位置,然后根据各象限点的坐标特征写出A,B,C三点的坐标;
(2)利用D和E点坐标标出超市和邮局的位置;
(3)求出CD的长即可得到小强家到超市的实际距离.
【详解】(1)如图,A(3,2),B(﹣2,1),C(6,﹣3);
(2)如图;
(3)CD=700,所以小强家到超市的实际距离为700m.
【点睛】本题考查了坐标确定位置:平面内的点与有序实数对一一对应;记住直角坐标系中特殊位置点的坐标特征.
22.(1)风云堂表示为(5,5),碧水池表示为(6,1).(2)风云堂位于西湖的北偏东45°方向且距西湖3个单位处.
【分析】先画出直角坐标系,然后利用方格图写出各景点的坐标和距离和方向角表示出风云堂相对于西湖的位置.
【详解】解:如图,
(1)风云堂表示为(5,5),碧水池表示为(6,1).(2)风云堂位于西湖的北偏东45°方向且距西湖3个单位处.
【点睛】本题考查坐标确定位置:直角坐标平面内点的位置由有序实数对确定,有序实数对与点一一对应.
23.(1)1,
(2)图见解析;教学楼坐标为,体育馆的坐标为
【分析】(1)根据已知点坐标得到原点位置,进而作出平面直角坐标系,即可得出答案;
(2)根据(1)中平面直角坐标系可得答案.
【详解】(1)解:根据题意,画出直角直角坐标系如图:
由图知,艺术楼的坐标为,实验楼的坐标为,
∴,.
故答案为:1,;
(2)解:平面直角坐标系如上图所示;
由图可知,教学楼坐标为,体育馆的坐标为.
【点睛】本题考查坐标确定位置,正确得到原点位置并画出平面直角坐标系是解答的关键.
24.(1)汽车站(1,1),消防站(2,﹣2);(2)(2)小英经过的地方:游乐场,公园,姥姥家,宠物店,邮局.
【分析】(1)根据平面直角坐标系直接写出坐标即可;(2)根据平面直角坐标系找出各点对应的位置,然后写出经过的地方.
【详解】(1)汽车站(1,1),消防站(2,﹣2);
(2)小英经过的地方:游乐场,公园,姥姥家,宠物店,邮局.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
