20.2 函数 同步练习（含解析）

中小学教育资源及组卷应用平台
20.2函数
学校:___________姓名：___________班级：___________考号：___________
一、单选题
1．下列各图象中，是的函数的是（ ）
A． B．
C． D．
2．下列关系中，y不是x的函数的是（ ）
A． B． C． D．
3．已知球的表面积与它的半径之间的关系式是，其中随的变化而变化，则在这个公式中变量是（ ）
A．， B．， C． D．，，
4．下列曲线中，不能表示是的函数的是（ ）
A． B．
C． D．
5．下列变量之间的关系中，是函数关系的是 ( )
A．人的体重与年龄 B．正方形的周长与边长
C．长方形的面积与长 D．y=±中，y与x
6．下表反映的是某地区电的使用量x（千瓦时）与应交电费y（元）之间的关系，下列说法不正确的是（ ）
用电量x（千瓦时） 1 2 3 4 …
应交电费y（元） 0.55 1.1 1.65 2.2 …
A．x与y都是变量，且x是自变量，y是x的函数
B．用电量每增加1千瓦时，电费增加0.55元
C．若用电量为8千瓦时，则应交电费4.4元
D．y不是x的函数
7．已知集合，且
使中元素和中的元素对应，则的值分别为（）
A． B． C． D．
8．为预防新冠肺炎，某校定期对教室进行消毒水消毒，测出药物喷洒后每立方米空气中的含药量y（mg）和时间x（min）的数据如表：
时间x（min） 2 4 6 8
含药量y（mg） 16 14 12 10
则下列叙述错误的是（ ）
A．时间为14min时，室内每立方米空气中的含药量为4mg
B．在一定范围内，时间越长，室内每立方米空气中的含药量越小
C．挥发时间每增加2min，室内每立方米空气中的含药量减少2mg
D．室内每立方米空气中的含药量是自变量
9．下列图像不能表示是的函数的是（ ）
A． B． C． D．
10．下列关系式中，y不是x的函数的是（ ）
A． B． C． D．
11．给出下列式子：①；②；③；④；⑤．其中y是x的函数的有（ ）
A．2个 B．3个 C．4个 D．5个
12．设函数，以下结论正确的是（ ）.
A． B．若，则
C． D．
二、填空题
13．表示函数之间的关系常用 、 、 三种方法.
14．我们解答过一些求代数式的值的题目，请把下面的问题补充完整：
当x的值分别取-5、0、1…时，3x2-2x+4的值分别为89、4、5…根据函数的定义，可以把x看做自变量，把 看做因变量，那么因变量 （填“是”或“不是”）自变量x的函数，理由是 .
15．在面积为120m 的长方形中，它的长（m）与宽（m）的函数解析式是 .
16．果字成熟后从树上落到地面，它落下的高度与经过的时间有如下的关系：
时间（秒） 0.5 0.6 0.7 0.8 0.9 1
落下的高度（米）
如果果子经过2秒落到地上，那么此果子开始落下时离地面的高度大约是 米．
17．下列与的关系中，不是的函数关系的是 ．（填序号）
①；②；③；④； ⑤；⑥．
三、解答题
18．根据经验，跳远的距离（v是助跑的速度，米/秒），其中变量s随着哪一个量的变化而变化？
19．心理学家研究发现，学生对一个新概念的接受能力y与提出这个新概念所用的时间x（单位：）之间有如下表所示的关系（其中）：
提出一个新概念所用的时间 2 5 7 10 12 13 14 17 20
对这个新概念的接受能力y 47.8 53.5 56.3 59 59.8 59.9 59.8 58.3 55
(1)上表反映了哪两个变量之间的关系？哪个是自变量？哪个是因变量？
(2)根据表格中的数据，当提出一个新概念所用的时间是 时，学生对这个新概念的接受能力最强；
(3)学生对一个新概念的接受能力在什么时间段内逐渐增强？在什么时间段内逐渐减弱？
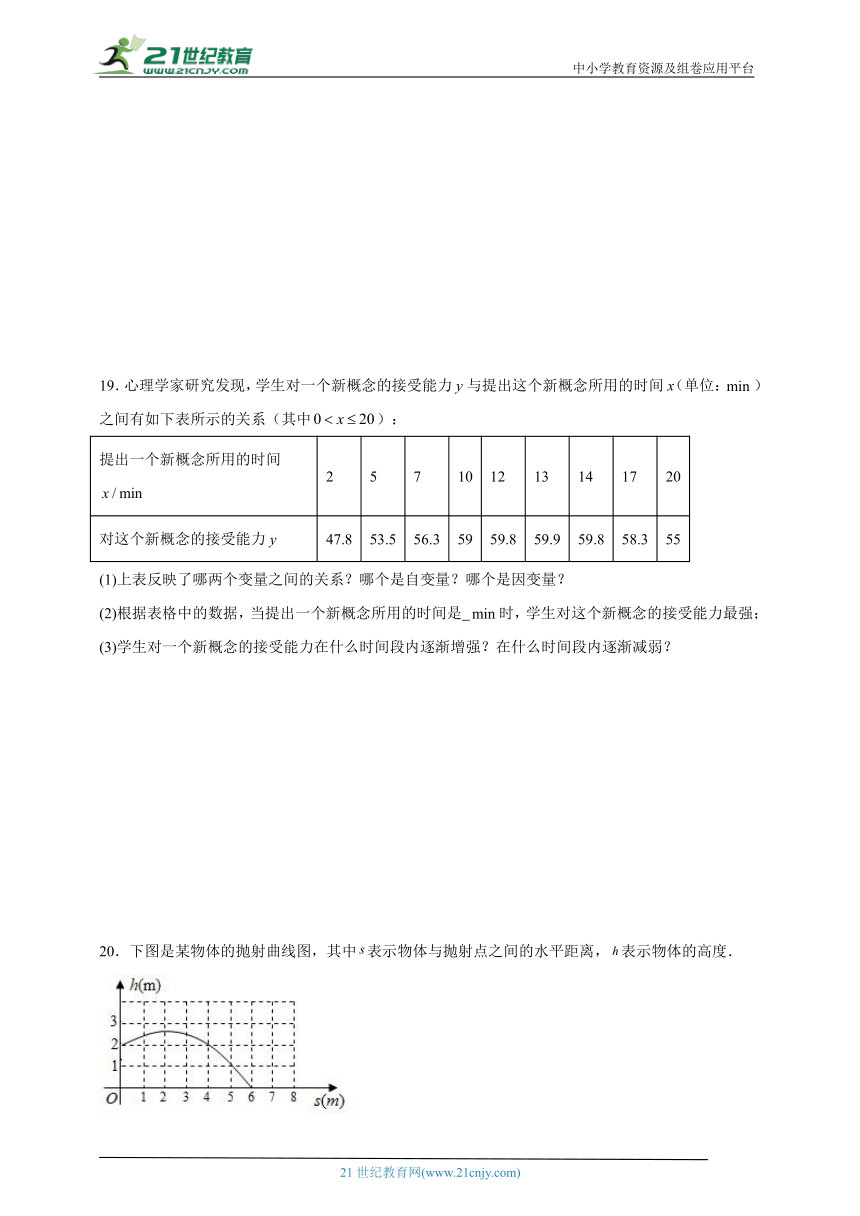
20．下图是某物体的抛射曲线图，其中表示物体与抛射点之间的水平距离，表示物体的高度．
（1）这个图象反映了哪两个变量之间的关系？
（2）根据图象填表：
0 1 2 3 4 5 6
（3）当距离取之间的一个确定的值时，相应的高度确定吗？
（4）高度可以看成距离的函数吗？
21．已知x为实数．y、z与x的关系如表格所示：根据上述表格中的数字变化规律，解答下列问题：
（1）当x为何值时，y=430？
（2）当x为何值时，y=z？
x y z
… … …
3 30×3+70 2×1×8
4 30×4+70 2×2×9
5 30×5+70 2×3×10
6 30×6+70 2×4×11
… … …
22．下表是某城市2012年统计的中小学男学生各年龄组的平均身高：
年龄组（岁） 7 8 9 10 11 12 13 14 15 16 17 18
平均身高 117 121 125 130 135 142 148 155 162 167 170 172
观察此表，回答下列问题：
（1）该市14岁男学生的平均身高是多少？
（2）该市男学生的平均身高从哪一岁开始增加特别迅速？
（3）这里反映了哪些变量之间的关系？其中哪个是自变量？哪个是因变量？
23．指出下面各关系式中的常量与变量．运动员在400m一圈的跑道上训练，他跑一圈所用的时间t（s）与跑步速度v（m/s）之间的函数关系式为t=．
24．心理学家发现,学生对概念的接受能力y与提出概念所用的时间x(单位:min)之间有如下关系(其中0≤x≤20):
提出概念所用时间x/min 2 5 7 10 12 13 14 17 20
对概念的接受能力y 47.8 53.5 56.3 59 59.8 59.9 59.8 58.3 55
　(注:接受能力值越大,说明学生的接受能力越强)
(1)上表中反映了哪两个变量之间的关系 哪个是自变量 哪个是因变量
(2)当提出概念所用时间是10 min时,学生的接受能力是多少
(3)根据表格中的数据,你认为提出概念所用时间为多少时,学生的接受能力最强
(4)从表格中可知,当提出概念所用时间x在什么范围内时,学生的接受能力逐步增强 当提出概念所用时间x在什么范围内时,学生的接受能力逐步降低
《20.2函数》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A D B A B D D D B C
题号 11 12
答案 B D
1．A
【分析】本题考查了函数的概念，深刻理解函数的概念是解题的关键：函数的定义：一般地，在一个变化过程中，如果有两个变量与，并且对于的每一个确定的值，都有唯一确定的值与其对应，那么我们就说是自变量，是的函数．对函数概念的理解，主要抓住以下三点：（1）有两个变量；（2）一个变量的数值随着另一个变量的数值的变化而变化；（3）对于自变量每一个确定的值，函数有且只有一个值与之对应．注意事项：判断两个变量是否有函数关系，不仅看它们之间是否有关系式存在，更重要的是看对于的每一个确定的值，是否有唯一确定的值与其对应；函数不是数，它是指某一变化过程中两个变量之间的关系．函数的意义反映在图象上一个简单的判断方法是：作垂直轴的直线在左右平移的过程中与函数图象只会有一个交点．
根据函数的概念逐项分析判断即可．
【详解】解：A、根据图象可知，给一个值，有且只有个值与其对应，满足函数的定义，故选项符合题意；
B、根据图象可知，给一个值，有不止个值与其对应，不满足函数的定义，故选项不符合题意；
C、根据图象可知，给一个值，有不止个值与其对应，不满足函数的定义，故选项不符合题意；
D、根据图象可知，给一个值，有不止个值与其对应，不满足函数的定义，故选项不符合题意；
故选：．
2．D
【分析】根据函数的定义即可求解．
【详解】解：A、中，y是x的函数，故此选项不合题意；
B、中，y是x的函数，故此选项不合题意；
C、中，y是x的函数，故此选项不合题意；
D、中，y不是x的函数，故此选项符合题意；
故选：D．
【点睛】此题主要考查函数的识别判断，解题的关键是熟知函数定义的理解．
3．B
【分析】此题主要考查了常量和变量，关键是掌握定义．根据变量和常量的定义：在一个变化的过程中，数值发生变化的量称为变量；数值始终不变的量称为常量，可直接得到答案．
【详解】解：中，常量是4，，变量是、，
故选：B．
4．A
【分析】本题考查函数的概念，关键是掌握函数的定义．
设在一个变化过程中有两个变量与，对于的每一个确定的值，都有唯一的值与其对应，那么就说是的函数，由此即可判断．
【详解】解：A、不符合函数的定义，不是的函数，故此选项符合题意；
B、符合函数的定义，是的函数，故此选项不符合题意；
C、符合函数的定义，是的函数，故此选项不符合题意；
D、符合函数的定义，是的函数，故此选项不符合题意；
故选：A．
5．B
【详解】A. 人的体重与年龄不成函数关系，故不正确；
B. ∵正方形的周长=边长×4，∴正方形的周长与边长成函数关系，故正确；
C. 长方形的面积=长×宽，有两个变量，故不正确；
D. y=±中，y与x不成函数关系，故不正确；
故选B.
6．D
【分析】结合表格中数据变化规律进而得出y是x的函数且用电量每增加1千瓦时，电费增加0.55元．
【详解】解：A、x与y都是变量，且x是自变量，y是x的函数，正确，不合题意；
B、用电量每增加1千瓦时，电费增加0.55元，正确，不合题意；
C、若用电量为8千瓦时，则应交电费元，正确，不合题意；
D、y是x的函数，原说法错误，符合题意．
故选：D．
【点睛】此题考查了函数的概念以及常量与变量，正确获取信息是解题关键．
7．D
【详解】按照对应法则，
而，∴
故选D.
8．D
【分析】根据表中数据表示出函数的解析式以及表格，两个变量之间的变化关系即可正确解答本题．
【详解】解：根据表格数据可以得出两个变量的关系式为y＝ x＋18，
A、当x＝14min时，y＝ 14＋18＝4mg，故选项不符合题意；
B、在一定范围内，燃烧时间越长，室内每立方米空气中的含药量越小，故选项不符合题意；
C、挥发时间每增加2min，室内每立方米空气中的含药量减少2mg，故选项不符合题意；
D、因为室内每立方米空气中的含药量随时间的变化而变化，所以时间是自变量，每立方米空气中的含药量是时间的函数，故选项符合题意．
故选：D．
【点睛】本题考查了函数的定义和性质，解题关键是能读懂表格中数据的特征，理解函数的定义．
9．B
【分析】根据函数的图象可知对于x的每一个值y都有唯一的值与之相对应进行判定即可．
【详解】根据函数的概念：如果在一个变化过程中，有两个变量x、y，对于x的每一个值，y都有唯一确定的值与之对应，这时称y是x的函数．
选项B，对于一个x有两个y与之对应，故不是函数图象，
故选：B．
【点睛】本题主要考查了函数的图象，以及函数的表示方法，解题的关键是函数的定义，属于基础题．
10．C
【分析】根据函数的概念可知，满足对于x的每一个取值，y都有唯一确定的值与之对应关系，据此分析每一选项即可得出答案．
【详解】A． 符合函数定义，是函数，故选项错误，不符合题意；
B． 符合函数定义，是函数，故选项错误，不符合题意；
C． 对于x的每一个取值（），y都有两个值，不是函数，故选项正确，符合题意；
D． 符合函数定义，是函数，故选项错误，不符合题意．
故选：C
【点睛】本题考查了函数的定义，一般地，在一个变化过程中有两个变量x与y，对于x的每一个确定的值，y都有唯一的值与其对应，那么就说y是x的函数，x是自变量．
11．B
【分析】根据以下特征进行判断即可：①有两个变量；②一个变量的数值随着另一个变量的数值的变化而发生变化；③对于自变量的每一个确定的值，函数值有且只有一个值与之对应．
【详解】①，y是x的函数；
②，y是x的函数；
③中有x，y，z三个变量，因此不能说y是x的函数；
④中当x取任一正数值时，有两个y值与之对应，故y不是x的函数．
⑤，y是x的函数.
故选B．
【点睛】本题主要考查的是函数的概念，掌握函数的定义是解题的关键．
12．D
【分析】中x即自变量，把自变量的值代入解析式计算，然后进行判断即可．
【详解】f(a)+f( a)=a(a 1) a( a 1)=2a2，A不正确；
f(a)=a,即a(a 1)=a，即a(a 2)=0，则a=0或2，B不正确；
f(a)f(-a)=a(a 1)×[ a( a 1)]= a4- a2，C不正确；
f(a)= a(a 1),f(1 a)=(1-a)(1-a-1)=(1-a)(-a)= a(a 1)，D正确，
故选D.
【点睛】本题考查求函数值，在本题中代入自变量时需注意当自变量为-a或1-a时需将-a或1-a看成一个整体，去替换关系式中的x.还需注意化简时的符号问题.
13． 列表法 图像法 解析式法
【分析】根据表示函数之间的关系方法直接回答即可.
【详解】表示函数之间的关系常用列表法、图像法、解析式法三种方法.
【点睛】本题主要考查函数的概念，熟练掌握函数的基础知识是解决本题的关键.
14． 代数式的值 是 对于自变量每取一个值，因变量都有唯一确定的值与它对应
【详解】当x的值分别取－5、0、1…时，3x2－2x+4的值分别为89、4、5…根据函数的定义，可以把x看做自变量，把代数式的值看做因变量，那么因变量是自变量x的函数，理由是对于自变量每取一个值，因变量都有唯一确定的值与它对应.
故答案为(1).代数式的值；(2).是；(3).对于自变量每取一个值，因变量都有唯一确定的值与它对应.
15．
【分析】根据长方形的面积公式可得，进而变形即可得y关于x的函数解析式.
【详解】∵长方形的面积=长×宽，
∴，
∴.
【点睛】本题考查用关系式法表示变量之间的关系. 能利用矩形的面积公式中的等量关系列出关系式是解决此题的关键.
16．20
【分析】分析表格中数据，得到物体自由下落的高度随着时间的增大而增大，与的关系为：，把代入，再进行计算即可．
【详解】解：由表格得，用时间表示高度的关系式为：，
当时，．
所以果子开始落下时离地面的高度大约是20米．
故答案为：20．
【点睛】本题考查了根据图表找规律，并应用规律解决问题，要求有较强的分析数据和描述数据的能力．能够正确找到和的关系是解题的关键．
17．②③
【分析】本题考查函数定义，解题的关键是理解掌握自变量x在一定的范围内取一个值，因变量y有唯一确定的值与之对应，则y叫x的函数．根据函数的定义，自变量x在一定的范围内取一个值，因变量y有唯一确定的值与之对应，则y叫x的函数，即可得出答案．
【详解】解：根据题意得①、④、⑤和⑥满足取一个x的值，有唯一确定的y值和它对应，y是x的函数，而②和③对一个x的值，与之对应的可能有两个y的值，故②和③y不是x的函数，
故答案为：②③．
18．变量s随着v的变化而变化．
【分析】根据变量和常量的定义：在一个变化的过程中，数值发生变化的量称为变量；数值始终不变的量称为常量可直接得到答案．
【详解】解：中，常量是，变量是s、v，
其中变量s随着v的变化而变化．
【点睛】此题主要考查了常量和变量，关键是掌握定义．
19．(1)反映了提出一个新概念所用的时间x与学生对这个新概念的接受能力y之间的关系，其中提出一个新概念所用的时间x是自变量，学生对这个新概念的接受能力y是因变量
(2)13
(3)学生对一个新概念的接受能力在时间段内逐渐增强，在时间段内逐渐减弱
【分析】本题考查用表格表示变量之间的关系，理解自变量、因变量的意义以及变化关系是解决问题的关键．
（1）根据表格中提供的数量的变化关系，得出答案；
（2）根据表格中两个变量变化的数据可得出答案；
（3）根据表格提供变化情况得出结论．
【详解】（1）解：题表反映了提出一个新概念所用的时间x与学生对这个新概念的接受能力y之间的关系，其中提出一个新概念所用的时间x是自变量，学生对这个新概念的接受能力y是因变量．
（2）解：由题意可得：当提出一个新概念所用的时间是时，学生对这个新概念的接受能力最强；
（3）解：由表格中的数据可知，学生对一个新概念的接受能力在时间段内逐渐增强，在时间段内逐渐减弱．
20．（1）反映了拋射距离与高度之间的关系；（2）2.0，2.5，2.65，2.5，2.0，1.2，0；（3）确定；（4）可以
【分析】（1）根据变量的定义，即可求解；
（2）根据图象填表即可；
（3）根据这一范围内对于任一个距离，对应的函数值高度是唯一的，即可得到相应的高度是确定的；
（4）根据函数的定义，即可求解．
【详解】解：（1）根据题意得：这个图象反映了高度与拋射水平距离之间的关系；
（2）根据图象填表如下：
0 1 2 3 4 5 6
2.0 2.5 2.65 2.5 2.0 1.2 0
（3）当距离取之间的一个确定的值时，相应的高度是确定的，
理由如下：因为这一范围内对于任一个距离，对应的函数值高度是唯一的，所以相应的高度是确定的；
（4）∵高度随距离的变化而变化，并且对于任一个距离，对应的函数值高度是唯一的，
∴高度可以看成距离的函数．
【点睛】本题主要考查了函数与变量，熟练掌握设在一个变化过程中有两个变量x与y，对于x的每一个确定的值，y都有唯一的值与其对应，那么就说y是x的函数，x是自变量是解题的关键．
21．(1)x=12;(2)x=-3或15
【分析】由图片中的信息可得出:当x为n(n3)时,y应该表示为30×n+70,z就应该表示为2×（n-2）(5+n);那么由此可得出（1）（2）中所求的值.
【详解】解：∵y=30×x+70，z=2×（x﹣2）（5+x）
（1）当x=12时，y=30×12+70=430；
（2）∵y=z，
即30×x+70=2×（x﹣2）（5+x），
解得：x=﹣3或15．
【点睛】本题考查了用表格表示变量之间的关系,中等难度,从例子中找到规律是解题关键.
22．（1）；（2）11 岁；（3）年龄和身高，年龄，身高
【分析】(1)根据表格中的数据，可直接回答；
(2)求出每年的增加数，进行比较即可；
(3)根据变量的关系确定自变量和因变量即可．
【详解】解:（1）由表中数据可得：该市14岁男学生的平均身高是；
（2）该市男学生的平均身高每年增加依次为：4、4、5、5、7、6、7、7、5、3、2；
故该市男学生的平均身高从 11 岁开始增加特别迅速．
（3）这里反映了年龄和身高两个变量之间的关系，其中身高随着年龄的变化而变化，故年龄是自变量，身高是因变量．
【点睛】本题考查函数的表示方法，解答本题的关键是明确题意，找出所求问题需要的条件解答．
23．常量是400m，变量是v、t
【分析】根据常量是变化过程中保持不变的量,变化过程中变化的量是变量,可得答案.
【详解】解：运动员在400m一圈的跑道上训练，他跑一圈所用的时间t（s）与跑步速度v（m/s）之间的函数关系式为t=，
常量是400m，变量是v、t．
【点睛】本题考查了常量与变量,常量是变化过程中保持不变的量,变化过程中变化的量是变量.属于简单题,熟悉概念是解题关键.
24．(1)反映了提出概念所用的时间x和对概念的接受能力y两个变量之间的关系;其中x是自变量,y是因变量.
(2) 59.
(3)所用时间为13 min时,学生的接受能力最强.
(4)当x在2至13的范围内,学生的接受能力逐步增强;当x在13至20的范围内,学生的接受能力逐步降低.
【详解】分析：(1)由条件可知两个变量是提出概念所用的时间和对概念的接受能力，对概念的接受能力随着时间的变化而变化；
(2)直接从表中读出提出概念时间是10时对应的接受能力；
(3)从表中读出接受能力最大时对应的时间；
(4)根据接受能力的增大和减小过程得到对应的x的范围.
本题解析： (1)提出概念所用的时间x和对概念接受能力y两个变量，其中x是自变量，y是因变量；
(2)提出概念10分钟时，学生的接受能力是59；
(3)学生接受能力最强是59.9，对应的时间是13，
所以提出概念13分钟时学生的接受能力最强；
(4)2分钟至13分钟时学生接受能力逐步增强，13分钟至20分钟时逐步降低.
点睛：用表格可以表示变量之间的关系，根据表格中的数据，可以对数据的变化趋势进行预测.因变量随着自变量的变化而变化.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)