20.4函数的初步应用同步练习(含解析)
文档属性
| 名称 | 20.4函数的初步应用同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 995.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 17:27:29 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
20.4函数的初步应用
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.小颖家、图书馆、体育馆依次在一条直线上.周六小颖从家出发步行来到图书馆,在图书馆学习了一段时间后,又从图书馆乘车去体育馆锻炼,下面能反映小颖离家的路程y与出发时间x的函数关系的大致图象是( )
A. B.
C. D.
2.甲、乙两人沿相同的路线由A地到B地匀速前进,A,B两地间的路程为20km.他们前进的路程为s(km),甲出发后的时间为t(h),甲、乙前进的路程与时间的函数图象如图所示.下列结论:①乙比甲晚出发1小时;②甲比乙晚到B地3小时;③甲的速度是5千米/时;④乙的速度是20千米/小时;根据图象信息,你认为错误的结论个数是( )
A.1个 B.2个 C.3个 D.4个
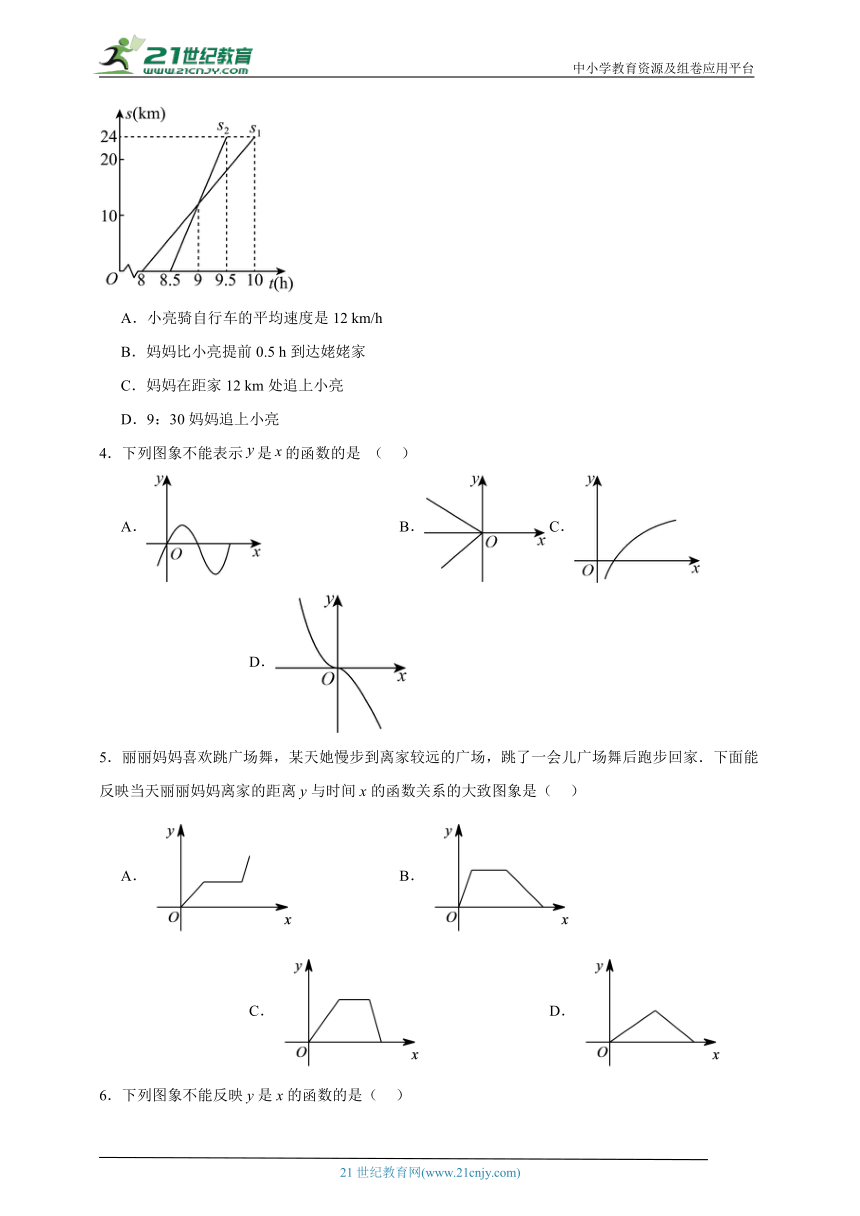
3.小亮家与姥姥家相距24 km,小亮8:00从家出发,骑自行车去姥姥家.妈妈8:30从家出发,乘车沿相同路线去姥姥家.在同一直角坐标系中,小亮和妈妈的行进路程s(km)与时间t(h)的函数图象如图所示.根据图象得出下列结论,其中错误的是( )
A.小亮骑自行车的平均速度是12 km/h
B.妈妈比小亮提前0.5 h到达姥姥家
C.妈妈在距家12 km处追上小亮
D.9:30妈妈追上小亮
4.下列图象不能表示是的函数的是 ( )
A. B. C. D.
5.丽丽妈妈喜欢跳广场舞,某天她慢步到离家较远的广场,跳了一会儿广场舞后跑步回家.下面能反映当天丽丽妈妈离家的距离y与时间x的函数关系的大致图象是( )
A. B. C. D.
6.下列图象不能反映y是x的函数的是( )
A. B.
C. D.
7.甲地和乙地之间有一条长为千米的直路,,两辆小汽车都在该条直路上,目的地都是乙地,速度分别为和.行驶前,车在甲地,车在车前面处,若两车同时行驶,则从开始行驶到其中一辆车先到达乙地的过程中,两车之间的距离与时间之间的函数图象是( )
A. B.
C. D.
8.【卷号】1574244236926976
【题号】1574244242350080
8.
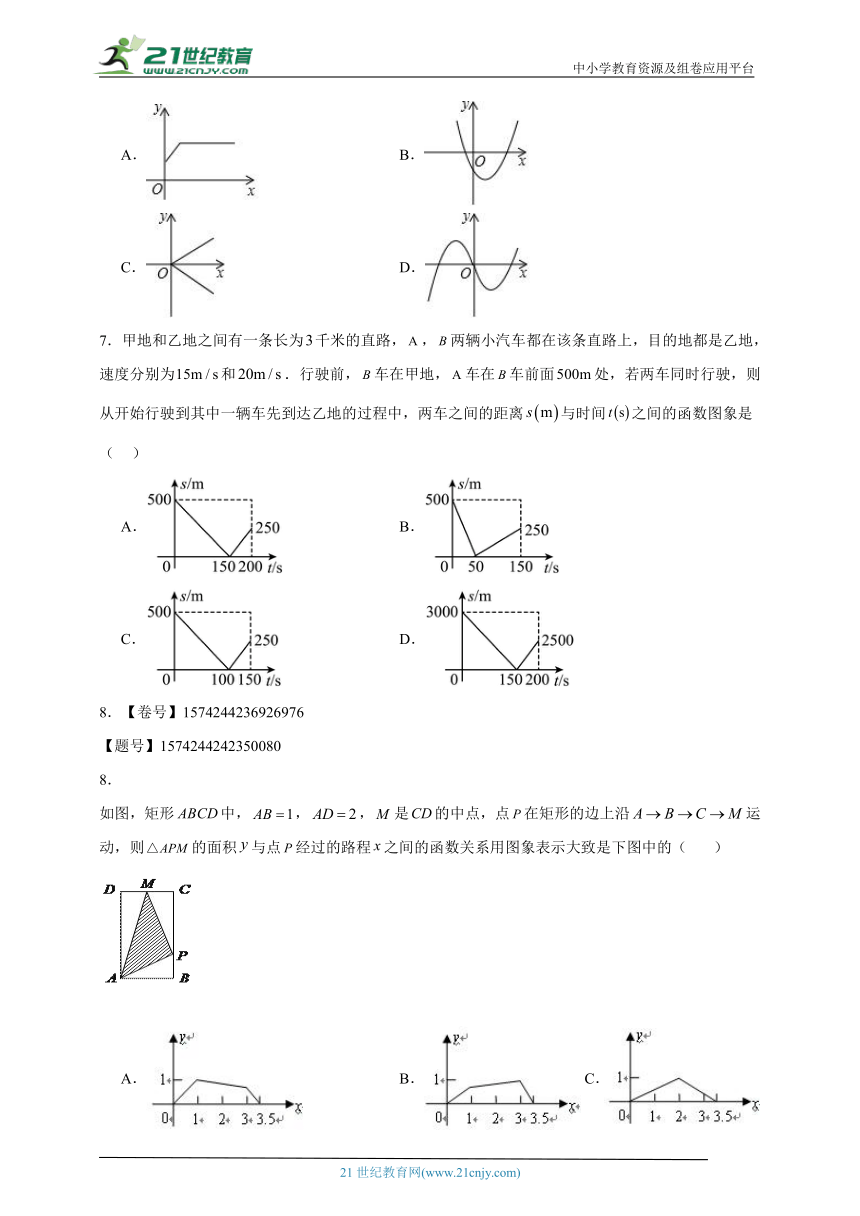
如图,矩形中,,,是的中点,点在矩形的边上沿运动,则的面积与点经过的路程之间的函数关系用图象表示大致是下图中的( )
A. B. C. D.
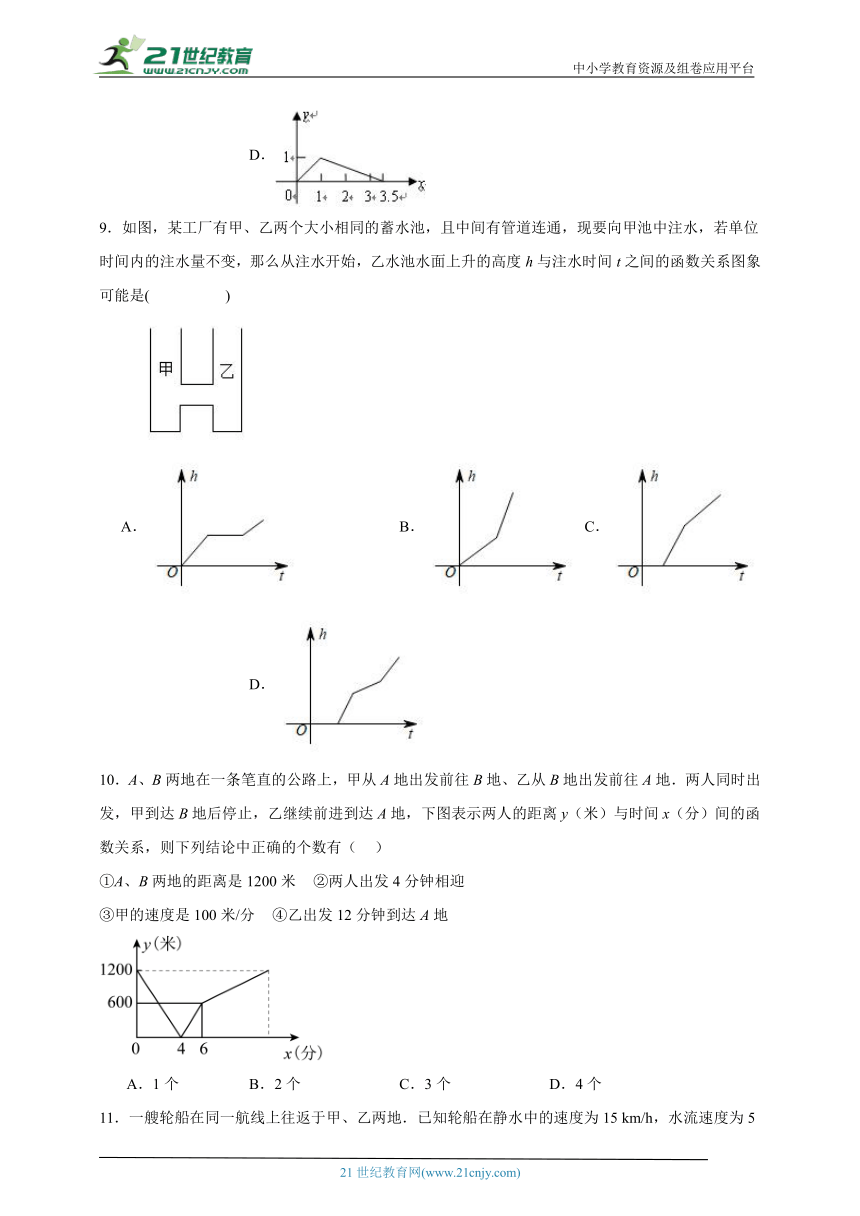
9.如图,某工厂有甲、乙两个大小相同的蓄水池,且中间有管道连通,现要向甲池中注水,若单位时间内的注水量不变,那么从注水开始,乙水池水面上升的高度h与注水时间t之间的函数关系图象可能是( )
A. B. C. D.
10.A、B两地在一条笔直的公路上,甲从A地出发前往B地、乙从B地出发前往A地.两人同时出发,甲到达B地后停止,乙继续前进到达A地,下图表示两人的距离y(米)与时间x(分)间的函数关系,则下列结论中正确的个数有( )
①A、B两地的距离是1200米 ②两人出发4分钟相迎
③甲的速度是100米/分 ④乙出发12分钟到达A地
A.1个 B.2个 C.3个 D.4个
11.一艘轮船在同一航线上往返于甲、乙两地.已知轮船在静水中的速度为15 km/h,水流速度为5 km/h.轮船先从甲地顺水航行到乙地,在乙地停留一段时间后,又从乙地逆水航行返回到甲地.设轮船从甲地出发后所用时间为t(h),航行的路程为s(km),则s与t的函数图象大致是( )
A. B. C. D.
12.如图,已知在Rt△ABC中,∠C=90°,AC=6,BC=8,点E是边AC上一动点,过点E作EF∥BC,交AB边于点F,且,点D为BC上任一点,连接DE,DF.设EC的长为x,则△DEF的面积y关于x的函数关系大致为( )
A.A B.B C.C D.D
二、填空题
13.跳台滑雪是冬奥会比赛项目之一,一名参赛运动员起跳后,飞行路线如图所示.若h(单位:m)表示飞行高度,s(单位:m)表示运动员与滑出点的水平距离,则这名运动员起跳后的最大飞行高度是 m.
14.如图反映的过程是:小刚从家去菜地浇水,又去青稞地锄草,然后回家.已知菜地与青稞地的距离为a千米,小刚在青稞地锄草比在菜地浇水多用了b分钟,则a,b的值分别为 .
15.某农场租用收割机收割小麦,甲收割机单独收割2天后,又调来乙收割机参与收割,直至完成800亩的收割任务,收割亩数与天数之间的关系如图所示,那么乙参与收割 天.
16.一个装有进水管和出水管的容器,开始时,先打开进水管注水,3分钟时,再打开出水管排水,8分钟时,关闭进水管,直至容器中的水全部排完.在整个过程中,容器中的水量y(升)与时间x(分钟)之间的函数关系如图所示,则图中a的值为 .
17.如图,为一个沙漏在计时过程中所剩沙子质量y(克)与时间x(小时)之间关系的图象,则从开始计时到沙子漏光所需的时间为 小时.
三、解答题
18.某高速公路上有A,B,C三地,A,B两地相距420千米.甲、乙两车分别从A,B两地同时出发,沿公路匀速相向而行,分别开往B,A两地.甲、乙两车到C地的路程y(千米)与行驶时间x(小时)的关系如图所示.
(1)请在直线AB上中标出C地的大致位置,并直接写出AC:BC的值;
(2)求甲车的速度,并求出图中b的值.
(3)求乙车的速度.
19.某车间的甲、乙两名工人分别同时生产同一种零件,他们一天生产零件的个数与生产时间的关系如图所示.
(1)根据图象填空:
甲、乙两人中, 先完成一天的生产任务在生产过程中, 因机器故障停止生产 小时
当 时,甲、乙生产的零件个数相等
(2)谁在哪一段时间内的生产速度最快,求该段时间内,他每小时生产零件的个数.
20.某车间有甲、乙两条生产线.在甲生产线已生产了200吨成品后,乙生产线开始投入生产,甲、乙两条生产线每天分别生产20吨和30吨成品.
(1)分别求出甲、乙两条生产线各自总产量(吨)与从乙开始投产以来所用时间(天)之间的函数关系式.
(2)作出上述两个函数在如图所示的直角坐标系中的图象,观察图象,分别指出第10天和第30天结束时,哪条生产线的总产量高?
21.一慢车和一快车沿相同路线从A地到B地,两车所行的路程s(千米)与慢车行驶的时间x(时)关系如图所示.根据图像解决下列问题:
(1)快车比慢车晚 小时出发,快车比慢车早到 小时.快车追上慢车时,快车行驶了 千米.
(2)求A、B两地相距多少千米?
22.下面是一位病人的体温记录图,看图回答下列问题:
(1)护士每隔几小时给病人量一次体温?
(2)这位病人的最高体温是多少摄氏度?最低体温是多少摄氏度?
(3)他在4月8日12时的体温是多少摄氏度?
(4)图中的横线表示什么?
(5)从图中看,这位病人的病情是恶化还是好转?
23.如图是甲、乙两人同一地点出发后,路程随时间变化的图象.
(1)此变化过程中, 是自变量, 是因变量;
(2)甲的速度 乙的速度(大于、等于、小于);
(3)6时表示 ;
(4)路程为150km,甲行驶了 小时,乙行驶了 小时;
(5)9时甲在乙的 (前面、后面、相同位置);
(6)乙比甲先走了3小时,对吗? .
24.小雪和小松分别从家和图书馆出发,沿同一条笔直的马路相向而行小雪开始跑步,中途在某地改为步行,且步行的速度为跑步速度的一半,小雪先出发5分钟后,小松才骑自行车匀速回家.小雪到达图书馆恰好用了35分钟.两人之间的距离与小雪离开出发地的时间之间的函数图象如图所示,请根据图象解答下列问题:
(1)小雪跑步的速度为多少米/分?
(2)小松骑自行车的速度为米/分?
(3)当小松到家时,小雪离图书馆的距离为多少米?
《20.4函数的初步应用》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A A D B C C C A D C
题号 11 12
答案 C D
1.A
【分析】根据题意,理清从家出发不行至图书馆,学习一段时间后去体育馆,对这三段分析得到相应图像,然后即可解题.
【详解】解:从家到图书馆应该是过原点的倾斜向上的线段;然后学习过程为水平的线段;然后又从图书馆乘车去体育馆过程为倾斜向上的线段;符合上述过程的图象为A选项.
故选:A.
【点睛】本题考查根据题意识别函数图象,注意画图象时的分段情况是解题的关键.
2.A
【分析】根据图象可知,甲比乙早出发1小时,但晚到2小时,从A地到B地,甲实际用4小时,乙实际用1小时,从而可求得甲、乙两人的速度.
【详解】解:由图象知,甲出发1小时后乙才出发,甲比乙晚到B地2小时.故①结论正确,②结论错误;
甲的速度是:20÷4=5(km/h),故③结论正确;
乙的速度是:20÷1=20(km/h),故④结论正确;
所以错误的结论个数是1个.
故选:A.
【点睛】本题考查了函数图象,观察图象,得到A、B两地的距离以及甲乙两人从A地到达B地的时间,从而求出两人的速度是解题的关键.
3.D
【分析】根据函数图象可知根据函数图象小亮去姥姥家所用时间为10﹣8=2小时,进而得到小亮骑自行车的平均速度,对应函数图象,得到妈妈到姥姥家所用的时间,根据交点坐标确定妈妈追上小亮所用时间,即可解答.
【详解】解:A、根据函数图象小亮去姥姥家所用时间为10﹣8=2小时,
∴小亮骑自行车的平均速度为:24÷2=12(km/h),故正确;
B、由图象可得,妈妈到姥姥家对应的时间t=9.5,小亮到姥姥家对应的时间t=10,10﹣9.5=0.5(小时),
∴妈妈比小亮提前0.5小时到达姥姥家,故正确;
C、由图象可知,当t=9时,妈妈追上小亮,此时小亮离家的时间为9﹣8=1小时,
∴小亮走的路程为:1×12=12km,
∴妈妈在距家12km出追上小亮,故正确;
D、由图象可知,当t=9时,妈妈追上小亮,故错误;
故选:D
【点睛】本题考查函数图像的应用,从图像中读取关键信息是解题的关键.
4.B
【分析】本题考查了函数图象的判断,根据函数的定义:对于的每一个取值,都有唯一确定的值与之对应进行即可,正确理解函数的定义是解题的关键.
【详解】、对每一个的值,都有唯一确定的值与之对应,是得函数;
、对给定的的值,有两个值与之对应,不是得函数;
、对每一个的值,都有唯一确定的值与之对应,是得函数;
、对每一个的值,都有唯一确定的值与之对应,是得函数;
故选:.
5.C
【分析】在每段中,根据离家的距离随时间的变化情况即可进行判断.
【详解】出门时丽丽妈妈是慢步,所以函数图象上升得平缓;跳了一会广场舞离家的距离不变;跑步回家离家越来越近,并且比出门时速度要快,所以下降得更快,符合题意的是C;
故选:C.
【点睛】本题考查函数图象,解题的关键是理解路程y的含义和直线的倾斜程度与速度的关系.
6.C
【详解】解:A.当x取一值时,y有唯一与它对应的值,y是x的函数,不符合题意;
B.当x取一值时,y有唯一与它对应的值,y是x的函数,;不符合题意
C.当x取一值时,y没有唯一与它对应的值,y不是x的函数,符合题意;
D.当x取一值时,y有唯一与它对应的值,y是x的函数,不符合题意.
故选C.
7.C
【分析】求得,两辆小汽车分别到达乙地所花费的时间,以及相遇的时间,即可求解.
【详解】解:时,,两辆小汽车相距,
小汽车到达乙地的时间为
小汽车到达乙地的时间为:
∵
∴小汽车在时到达乙地,
,两辆小汽车相遇的时间为,
即在时,两辆小汽车相遇,
结合选项,C符合;
故选:C
【点睛】此题考查了函数图像的应用,解题的关键是理解题意,找到题中的关键节点,读懂函数图象.
8.A
【详解】试题分析:当点P在AB上运动时(),△APM的面积从0增加到1;当点P在BC上运动时(),△APM的面积从1减小到0.5;当点P在CM上运动时(),△APM的面积从0.5减小到0,故本题选A.
点睛:本题主要考查的是动点问题与一次函数的图像结合题,难度中等.在解决有关动点问题的时候,我们一定要注意进行分类讨论,即点在哪一条线段上,根据点在哪一条线段上时,求出每条线段与未知数之间的关系,然后利用面积的求法得出函数解析式,必须要注意自变量的取值范围.
9.D
【分析】根据特殊点的实际意义即可求出答案.
【详解】解:该蓄水池就是一个连通器.开始时注入甲池,乙池无水,当甲池中水位到达与乙池的连接处时,乙池才开始注水,所以A、B不正确,此时甲池水位不变,所有水注入乙池,所以水位上升快.当乙池水位到达连接处时,所注入的水使甲乙两个水池同时升高,所以升高速度变慢.在乙池水位超过连通部分,甲和乙部分同时升高,但蓄水池底变小,此时比连通部分快.
故选:D.
【点睛】主要考查了函数图象的读图能力.要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件,结合实际意义得到正确的结论.
10.C
【分析】
整个过程分三段:两人4分钟相遇;再过2分钟后甲到达B地;乙继续前进直到终点A地;根据图象则可判断①②;由图象知,甲6分钟到达终点,此时乙才行了全程的一半,则可以求出甲行驶的速度,从而可求得乙到达A地的时间,因而可对③④作出判断.
【详解】由图象知,两人出发时相距1200米,即A、B两地的距离是1200米,故①正确;
由图象知,两人出发后4分钟相遇,故②正确;
由图象知,甲6分钟到达B地,则甲的速度为1200÷6=200(米/分钟),故③错误;
由图象知,乙6分钟时距离出发地600米,时间是6分钟,则乙还有600米的路程,还需6分钟,共需6×2=12(分),故④正确;
综上所述,正确的有:①②④,共3个;
故选:C.
【点睛】本题考查函数的图象,从函数图象中获取有关信息、弄清运动过程是解题的关键.
11.C
【详解】解:第一个阶段,逆水航行,用时较多;第二个阶段,在乙地停留一段时间,随着时间的增长,路程不再变化,函数图象将与x轴平行;第三个阶段,顺水航行,所走的路程继续增加,相对于第一个阶段,用时较少,
故选C.
12.D
【详解】∵EF∥BC,
∴△AEF∽△ABC,
∴ ,即,
∴EF=,
∴S=×x=
只有选项D符合.故选D.
点睛:本题考查了动点问题函数图象,主要利用了相似三角形的性质,求出S与x的函数关系式是解题的关键,也是本题的难点.
13.42
【分析】本题考查从函数图形获取信息,根据图形可知纵坐标h表示飞行高度,图中曲线最高点对应的h值为 42,即可得出答案.
【详解】从所给的飞行路线图中可以看到,纵坐标h表示飞行高度,图中曲线最高点对应的h值为 42,所以这名运动员起跳后的最大飞行高度是 ,
故答案为:42.
14.,
【分析】首先根据图象,分析函数的几个阶段,然后再根据题意,求出和的值即可.
【详解】解:此函数大致可分以下几个阶段:
①至分钟,小刚从家走到菜地;
②至分钟,小刚在菜地浇水;
③至分钟,小刚从菜地走到青稞地;
④至分钟,小刚在青稞地除草;
⑤至分钟,小刚从青稞地回到家;
综合上面的分析得:由③的过程知,(千米);
由②、④的过程知(分钟).
故答案为:,.
【点睛】本题考查了利用函数的图象获取信息、有理数的加减法,正确理解函数图象横纵坐标表示的意义是解题关键.
15.4
【详解】解:由图可知,甲、乙收割机每天共收割350-200=150亩,共同收割600亩,
所以,乙参与收割的天数是600÷150=4天.
故答案为4.
【点睛】此题主要考查学生的读图获取信息的能力,要注意分析其中的“关键点”.
16.
【分析】根据函数图像,结合题意分析分别求得进水速度和出水速度,即可求解.
【详解】解:依题意,3分钟进水30升,则进水速度为升/分钟,
3分钟时,再打开出水管排水,8分钟时,关闭进水管,直至容器中的水全部排完直至容器中的水全部排完,
则排水速度为升/分钟,
,
解得.
故答案为:.
【点睛】本题考查了函数图象问题,从函数图象获取信息是解题的关键.
17.
【分析】根据图象可得沙漏漏沙的速度,从而得出从开始计时到沙子漏光所需的时间.
【详解】解:沙漏漏沙的速度为:(克/小时),
∴从开始计时到沙子漏光所需的时间为:(小时).
故答案为:.
【点睛】】
【点评】本题考查了函数图象的应用,学会看函数图象,理解函数图象所反映的实际意义,从函数图象中获取信息,并且解决有关问题.
18.(1)如图所示见解析,4:3;(2)b的值为4;(3)乙车的速度为80km/h.
【分析】(1)利用图象与x轴的交点坐标得出AC,BC的长,进而得出答案;
(2)利用甲车行驶的距离与时间求出平均速度即可,进而得出b的值;
(3)利用甲的速度得出3小时乙行驶的距离进而得出他的速度.
【详解】(1)如图所示,
由题意结合图象的纵坐标得出:甲地到C地距离为:240km,乙地到C地距离为:180km,
∴AC=240,BC=180,
∴AC:BC的值为:4:3;
(2)∵由图象可得出:甲车420km一共行驶7小时,
∴420÷7=60(km/h),
240÷60=4,
故b的值为4;
(3)∵甲的速度为60km/h,
∴3小时甲行驶了180km,此时距C地60km,
∴此时乙已经行驶了:180+60=240(km),
∴乙的速度为:240÷3=80(km/h).
故答案为(1)如图所示见解析,4:3;(2)b的值为4;(3)乙车的速度为80km/h.
【点睛】本题考查函数的图象,自变量和函数值,解题的关键是从函数的图像获取路程时间等重要信息.
19.(1)甲;甲;;或
(2)
【分析】(1)根据图象直接填写即可;根据图象中两函数图象交点即为甲、乙生产的零件个数相等时的信息.
(2)根据图象即可得到生产速度最快的时间段,再根据题意即可求出最快的速度.
【详解】(1)由图象可知,甲先完成一天的生产任务在生产过程中,甲因机器故障停止生产小时
由图象可知,
当或时,两函数图象相交,即为甲、乙生产的零件个数相等
故为3或5.5时,甲、乙生产的零件个数相等.
(2)由图象可知甲在时内倾斜角度最大,生产速度快;
此时甲每小时生产零件的个数为(个).
【点睛】本题考查了从图象中获取信息,解题的关键是根据题意得到相关的信息.
20.(1)甲生产线生产时对应的函数关系式是;乙生产线生产时对应的函数关系式为
(2)第10天结束时,甲生产线的总产量高;第30天结束时,乙生产线的总产量高
【分析】(1)根据甲生产线已生产了200吨成品后,乙生产线开始投入生产,甲、乙两条生产线每天分别生产20吨和30吨成品列出对应的函数关系式即可;
(2)根据(1)所求,先求出两条生产线产量相同是在第几天,然后画出函数图象,观察函数图象即可得到答案.
【详解】(1)解:由题意可得:甲生产线生产时对应的函数关系式是;
乙生产线生产时对应的函数关系式为.
(2)令,解得,可知在第20天结束时,两条生产线的产量相同,
故甲生产线所对应的生产函数图象一定经过点(0,200)和(20,600);
乙生产线所对应的生产函数图象一定经过点(0,0)和(20,600).
作出图象如图所示.
由图象可知:第10天结束时,甲生产线的总产量高;第30天结束时,乙生产线的总产量高.
【点睛】本题主要考查了列函数关系式,从函数图象获取信息,正确理解题意列出函数关系式是解题的关键.
21.(1)2,4,276
(2)828千米
【分析】(1)根据函数图像中的数据,可以写出快车比慢车晚几小时出发,快车比慢车早到几小时,快车追上慢车时,快车行驶了多少千米;
(2)根据图像中的数据,可以计算出慢车的速度,然后根据路程=速度×时间,即可计算出A、B两地相距多少千米.
【详解】(1)解:由图像可得,
慢车比快车晚2小时出发,快车比慢车早到18﹣14=4(小时),快车追上慢车时,快行驶了276千米,
故答案为:2,4,276;
(2)解:由图像可得,
慢车的速度为:276÷6=46(千米/时),
46×18=828(千米),
答:A、B两地相距828千米.
【点睛】本题考查一次函数的应用,利用数形结合的思想解答是解答本题的关键.
22.见解析
【详解】试题分析:
(1)(3)观察、分析图象中的数据信息,结合题意即可得到相应答案;
(4)图中的横线表示人的正常体温:37℃;
(5)由图象可知,这位病人的体温逐渐趋近于正常体温,由此可知病人的病情在好转.
试题解析:
(1)观察图象可得:护士每隔6小时给病人测量一次体温;
(2)观察图象可得:这位病人的最高体温是39.5℃,最低体温是36.8℃;
(3)这位病人4月8日12时的体温是37.5℃;
(4)图中的横线表示人的正常体温是37℃;
(5)从图象的变化趋势看可以看出,这位病人的体温逐渐趋近于正常体温,
∴这位病人的病情在好转.
23.(1)t;s;(2)小于;(3)乙追赶上了甲;(4)9;4.5;(5)后面;(6)不对.
【分析】(1)根据自变量与因变量的含义得到时间是自变量,路程是因变量;
(2)甲走6小时行驶100千米,乙走3小时走100千米,则可得到他们的速度的大小;
(3)6时两图象相交,说明他们相遇;
(4)观察图象直接得到答案;
(5)观察图象观察得到;
(6)观察图象得到甲先出发3小时后,乙才开始出发.
【详解】解:(1)函数图象反映路程随时间变化的图象,则t是自变量,s是因变量;
故答案为:t,s;
(2)甲的速度是100÷6=千米/小时,乙的速度是100÷3=千米/小时,所以甲的速度小于乙的速度;
故答案为:小于;
(3)6时表示他们相遇,即乙追赶上了甲;
故答案为:乙追赶上了甲;
(4)路程为150千米,甲行驶9小时,乙行驶了7.5-3=4.5小时;
故答案为:9,4.5;
(5)t=9时,乙的图象在甲的上方,即乙行驶的路程远些,所以9时甲在乙的后面;
故答案为:后面;
(6)不对,是乙比甲晚走了3小时.
故答案为:不对.
24.(1)
(2)
(3)
【分析】(1)由函数图象可知小雪跑步5分钟的路程为米,即可根据路程速度时间求出答案;
(2)先求出小雪步行的速度,然后设小雪在第t分钟改为步行,根据小雪第分钟到达图书馆建立方程求出t的值,再由函数图象可知小雪改为步行时两人相距求出小松骑车的速度即可;
(3)先求出小松到家的时间,再根据路程速度时间求出答案即可.
【详解】(1)解:由函数图象可知小雪跑步5分钟的路程为,
∴小雪跑步的速度为;
(2)解:由(1)得小雪步行的速度为,
设小雪在第t分钟改为步行,
∴,
解得,
∴由函数图象可知,当第10分钟时,小雪改为步行,此时两人相距,
∴小松骑车的速度为;
(3)解:由(2)得小松到家的时间为,
∴小雪离图书馆的距离为.
【点睛】本题主要考查了从函数图象获取信息,一元一次方程的实际应用,正确读懂函数图象是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
20.4函数的初步应用
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.小颖家、图书馆、体育馆依次在一条直线上.周六小颖从家出发步行来到图书馆,在图书馆学习了一段时间后,又从图书馆乘车去体育馆锻炼,下面能反映小颖离家的路程y与出发时间x的函数关系的大致图象是( )
A. B.
C. D.
2.甲、乙两人沿相同的路线由A地到B地匀速前进,A,B两地间的路程为20km.他们前进的路程为s(km),甲出发后的时间为t(h),甲、乙前进的路程与时间的函数图象如图所示.下列结论:①乙比甲晚出发1小时;②甲比乙晚到B地3小时;③甲的速度是5千米/时;④乙的速度是20千米/小时;根据图象信息,你认为错误的结论个数是( )
A.1个 B.2个 C.3个 D.4个
3.小亮家与姥姥家相距24 km,小亮8:00从家出发,骑自行车去姥姥家.妈妈8:30从家出发,乘车沿相同路线去姥姥家.在同一直角坐标系中,小亮和妈妈的行进路程s(km)与时间t(h)的函数图象如图所示.根据图象得出下列结论,其中错误的是( )
A.小亮骑自行车的平均速度是12 km/h
B.妈妈比小亮提前0.5 h到达姥姥家
C.妈妈在距家12 km处追上小亮
D.9:30妈妈追上小亮
4.下列图象不能表示是的函数的是 ( )
A. B. C. D.
5.丽丽妈妈喜欢跳广场舞,某天她慢步到离家较远的广场,跳了一会儿广场舞后跑步回家.下面能反映当天丽丽妈妈离家的距离y与时间x的函数关系的大致图象是( )
A. B. C. D.
6.下列图象不能反映y是x的函数的是( )
A. B.
C. D.
7.甲地和乙地之间有一条长为千米的直路,,两辆小汽车都在该条直路上,目的地都是乙地,速度分别为和.行驶前,车在甲地,车在车前面处,若两车同时行驶,则从开始行驶到其中一辆车先到达乙地的过程中,两车之间的距离与时间之间的函数图象是( )
A. B.
C. D.
8.【卷号】1574244236926976
【题号】1574244242350080
8.
如图,矩形中,,,是的中点,点在矩形的边上沿运动,则的面积与点经过的路程之间的函数关系用图象表示大致是下图中的( )
A. B. C. D.
9.如图,某工厂有甲、乙两个大小相同的蓄水池,且中间有管道连通,现要向甲池中注水,若单位时间内的注水量不变,那么从注水开始,乙水池水面上升的高度h与注水时间t之间的函数关系图象可能是( )
A. B. C. D.
10.A、B两地在一条笔直的公路上,甲从A地出发前往B地、乙从B地出发前往A地.两人同时出发,甲到达B地后停止,乙继续前进到达A地,下图表示两人的距离y(米)与时间x(分)间的函数关系,则下列结论中正确的个数有( )
①A、B两地的距离是1200米 ②两人出发4分钟相迎
③甲的速度是100米/分 ④乙出发12分钟到达A地
A.1个 B.2个 C.3个 D.4个
11.一艘轮船在同一航线上往返于甲、乙两地.已知轮船在静水中的速度为15 km/h,水流速度为5 km/h.轮船先从甲地顺水航行到乙地,在乙地停留一段时间后,又从乙地逆水航行返回到甲地.设轮船从甲地出发后所用时间为t(h),航行的路程为s(km),则s与t的函数图象大致是( )
A. B. C. D.
12.如图,已知在Rt△ABC中,∠C=90°,AC=6,BC=8,点E是边AC上一动点,过点E作EF∥BC,交AB边于点F,且,点D为BC上任一点,连接DE,DF.设EC的长为x,则△DEF的面积y关于x的函数关系大致为( )
A.A B.B C.C D.D
二、填空题
13.跳台滑雪是冬奥会比赛项目之一,一名参赛运动员起跳后,飞行路线如图所示.若h(单位:m)表示飞行高度,s(单位:m)表示运动员与滑出点的水平距离,则这名运动员起跳后的最大飞行高度是 m.
14.如图反映的过程是:小刚从家去菜地浇水,又去青稞地锄草,然后回家.已知菜地与青稞地的距离为a千米,小刚在青稞地锄草比在菜地浇水多用了b分钟,则a,b的值分别为 .
15.某农场租用收割机收割小麦,甲收割机单独收割2天后,又调来乙收割机参与收割,直至完成800亩的收割任务,收割亩数与天数之间的关系如图所示,那么乙参与收割 天.
16.一个装有进水管和出水管的容器,开始时,先打开进水管注水,3分钟时,再打开出水管排水,8分钟时,关闭进水管,直至容器中的水全部排完.在整个过程中,容器中的水量y(升)与时间x(分钟)之间的函数关系如图所示,则图中a的值为 .
17.如图,为一个沙漏在计时过程中所剩沙子质量y(克)与时间x(小时)之间关系的图象,则从开始计时到沙子漏光所需的时间为 小时.
三、解答题
18.某高速公路上有A,B,C三地,A,B两地相距420千米.甲、乙两车分别从A,B两地同时出发,沿公路匀速相向而行,分别开往B,A两地.甲、乙两车到C地的路程y(千米)与行驶时间x(小时)的关系如图所示.
(1)请在直线AB上中标出C地的大致位置,并直接写出AC:BC的值;
(2)求甲车的速度,并求出图中b的值.
(3)求乙车的速度.
19.某车间的甲、乙两名工人分别同时生产同一种零件,他们一天生产零件的个数与生产时间的关系如图所示.
(1)根据图象填空:
甲、乙两人中, 先完成一天的生产任务在生产过程中, 因机器故障停止生产 小时
当 时,甲、乙生产的零件个数相等
(2)谁在哪一段时间内的生产速度最快,求该段时间内,他每小时生产零件的个数.
20.某车间有甲、乙两条生产线.在甲生产线已生产了200吨成品后,乙生产线开始投入生产,甲、乙两条生产线每天分别生产20吨和30吨成品.
(1)分别求出甲、乙两条生产线各自总产量(吨)与从乙开始投产以来所用时间(天)之间的函数关系式.
(2)作出上述两个函数在如图所示的直角坐标系中的图象,观察图象,分别指出第10天和第30天结束时,哪条生产线的总产量高?
21.一慢车和一快车沿相同路线从A地到B地,两车所行的路程s(千米)与慢车行驶的时间x(时)关系如图所示.根据图像解决下列问题:
(1)快车比慢车晚 小时出发,快车比慢车早到 小时.快车追上慢车时,快车行驶了 千米.
(2)求A、B两地相距多少千米?
22.下面是一位病人的体温记录图,看图回答下列问题:
(1)护士每隔几小时给病人量一次体温?
(2)这位病人的最高体温是多少摄氏度?最低体温是多少摄氏度?
(3)他在4月8日12时的体温是多少摄氏度?
(4)图中的横线表示什么?
(5)从图中看,这位病人的病情是恶化还是好转?
23.如图是甲、乙两人同一地点出发后,路程随时间变化的图象.
(1)此变化过程中, 是自变量, 是因变量;
(2)甲的速度 乙的速度(大于、等于、小于);
(3)6时表示 ;
(4)路程为150km,甲行驶了 小时,乙行驶了 小时;
(5)9时甲在乙的 (前面、后面、相同位置);
(6)乙比甲先走了3小时,对吗? .
24.小雪和小松分别从家和图书馆出发,沿同一条笔直的马路相向而行小雪开始跑步,中途在某地改为步行,且步行的速度为跑步速度的一半,小雪先出发5分钟后,小松才骑自行车匀速回家.小雪到达图书馆恰好用了35分钟.两人之间的距离与小雪离开出发地的时间之间的函数图象如图所示,请根据图象解答下列问题:
(1)小雪跑步的速度为多少米/分?
(2)小松骑自行车的速度为米/分?
(3)当小松到家时,小雪离图书馆的距离为多少米?
《20.4函数的初步应用》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A A D B C C C A D C
题号 11 12
答案 C D
1.A
【分析】根据题意,理清从家出发不行至图书馆,学习一段时间后去体育馆,对这三段分析得到相应图像,然后即可解题.
【详解】解:从家到图书馆应该是过原点的倾斜向上的线段;然后学习过程为水平的线段;然后又从图书馆乘车去体育馆过程为倾斜向上的线段;符合上述过程的图象为A选项.
故选:A.
【点睛】本题考查根据题意识别函数图象,注意画图象时的分段情况是解题的关键.
2.A
【分析】根据图象可知,甲比乙早出发1小时,但晚到2小时,从A地到B地,甲实际用4小时,乙实际用1小时,从而可求得甲、乙两人的速度.
【详解】解:由图象知,甲出发1小时后乙才出发,甲比乙晚到B地2小时.故①结论正确,②结论错误;
甲的速度是:20÷4=5(km/h),故③结论正确;
乙的速度是:20÷1=20(km/h),故④结论正确;
所以错误的结论个数是1个.
故选:A.
【点睛】本题考查了函数图象,观察图象,得到A、B两地的距离以及甲乙两人从A地到达B地的时间,从而求出两人的速度是解题的关键.
3.D
【分析】根据函数图象可知根据函数图象小亮去姥姥家所用时间为10﹣8=2小时,进而得到小亮骑自行车的平均速度,对应函数图象,得到妈妈到姥姥家所用的时间,根据交点坐标确定妈妈追上小亮所用时间,即可解答.
【详解】解:A、根据函数图象小亮去姥姥家所用时间为10﹣8=2小时,
∴小亮骑自行车的平均速度为:24÷2=12(km/h),故正确;
B、由图象可得,妈妈到姥姥家对应的时间t=9.5,小亮到姥姥家对应的时间t=10,10﹣9.5=0.5(小时),
∴妈妈比小亮提前0.5小时到达姥姥家,故正确;
C、由图象可知,当t=9时,妈妈追上小亮,此时小亮离家的时间为9﹣8=1小时,
∴小亮走的路程为:1×12=12km,
∴妈妈在距家12km出追上小亮,故正确;
D、由图象可知,当t=9时,妈妈追上小亮,故错误;
故选:D
【点睛】本题考查函数图像的应用,从图像中读取关键信息是解题的关键.
4.B
【分析】本题考查了函数图象的判断,根据函数的定义:对于的每一个取值,都有唯一确定的值与之对应进行即可,正确理解函数的定义是解题的关键.
【详解】、对每一个的值,都有唯一确定的值与之对应,是得函数;
、对给定的的值,有两个值与之对应,不是得函数;
、对每一个的值,都有唯一确定的值与之对应,是得函数;
、对每一个的值,都有唯一确定的值与之对应,是得函数;
故选:.
5.C
【分析】在每段中,根据离家的距离随时间的变化情况即可进行判断.
【详解】出门时丽丽妈妈是慢步,所以函数图象上升得平缓;跳了一会广场舞离家的距离不变;跑步回家离家越来越近,并且比出门时速度要快,所以下降得更快,符合题意的是C;
故选:C.
【点睛】本题考查函数图象,解题的关键是理解路程y的含义和直线的倾斜程度与速度的关系.
6.C
【详解】解:A.当x取一值时,y有唯一与它对应的值,y是x的函数,不符合题意;
B.当x取一值时,y有唯一与它对应的值,y是x的函数,;不符合题意
C.当x取一值时,y没有唯一与它对应的值,y不是x的函数,符合题意;
D.当x取一值时,y有唯一与它对应的值,y是x的函数,不符合题意.
故选C.
7.C
【分析】求得,两辆小汽车分别到达乙地所花费的时间,以及相遇的时间,即可求解.
【详解】解:时,,两辆小汽车相距,
小汽车到达乙地的时间为
小汽车到达乙地的时间为:
∵
∴小汽车在时到达乙地,
,两辆小汽车相遇的时间为,
即在时,两辆小汽车相遇,
结合选项,C符合;
故选:C
【点睛】此题考查了函数图像的应用,解题的关键是理解题意,找到题中的关键节点,读懂函数图象.
8.A
【详解】试题分析:当点P在AB上运动时(),△APM的面积从0增加到1;当点P在BC上运动时(),△APM的面积从1减小到0.5;当点P在CM上运动时(),△APM的面积从0.5减小到0,故本题选A.
点睛:本题主要考查的是动点问题与一次函数的图像结合题,难度中等.在解决有关动点问题的时候,我们一定要注意进行分类讨论,即点在哪一条线段上,根据点在哪一条线段上时,求出每条线段与未知数之间的关系,然后利用面积的求法得出函数解析式,必须要注意自变量的取值范围.
9.D
【分析】根据特殊点的实际意义即可求出答案.
【详解】解:该蓄水池就是一个连通器.开始时注入甲池,乙池无水,当甲池中水位到达与乙池的连接处时,乙池才开始注水,所以A、B不正确,此时甲池水位不变,所有水注入乙池,所以水位上升快.当乙池水位到达连接处时,所注入的水使甲乙两个水池同时升高,所以升高速度变慢.在乙池水位超过连通部分,甲和乙部分同时升高,但蓄水池底变小,此时比连通部分快.
故选:D.
【点睛】主要考查了函数图象的读图能力.要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件,结合实际意义得到正确的结论.
10.C
【分析】
整个过程分三段:两人4分钟相遇;再过2分钟后甲到达B地;乙继续前进直到终点A地;根据图象则可判断①②;由图象知,甲6分钟到达终点,此时乙才行了全程的一半,则可以求出甲行驶的速度,从而可求得乙到达A地的时间,因而可对③④作出判断.
【详解】由图象知,两人出发时相距1200米,即A、B两地的距离是1200米,故①正确;
由图象知,两人出发后4分钟相遇,故②正确;
由图象知,甲6分钟到达B地,则甲的速度为1200÷6=200(米/分钟),故③错误;
由图象知,乙6分钟时距离出发地600米,时间是6分钟,则乙还有600米的路程,还需6分钟,共需6×2=12(分),故④正确;
综上所述,正确的有:①②④,共3个;
故选:C.
【点睛】本题考查函数的图象,从函数图象中获取有关信息、弄清运动过程是解题的关键.
11.C
【详解】解:第一个阶段,逆水航行,用时较多;第二个阶段,在乙地停留一段时间,随着时间的增长,路程不再变化,函数图象将与x轴平行;第三个阶段,顺水航行,所走的路程继续增加,相对于第一个阶段,用时较少,
故选C.
12.D
【详解】∵EF∥BC,
∴△AEF∽△ABC,
∴ ,即,
∴EF=,
∴S=×x=
只有选项D符合.故选D.
点睛:本题考查了动点问题函数图象,主要利用了相似三角形的性质,求出S与x的函数关系式是解题的关键,也是本题的难点.
13.42
【分析】本题考查从函数图形获取信息,根据图形可知纵坐标h表示飞行高度,图中曲线最高点对应的h值为 42,即可得出答案.
【详解】从所给的飞行路线图中可以看到,纵坐标h表示飞行高度,图中曲线最高点对应的h值为 42,所以这名运动员起跳后的最大飞行高度是 ,
故答案为:42.
14.,
【分析】首先根据图象,分析函数的几个阶段,然后再根据题意,求出和的值即可.
【详解】解:此函数大致可分以下几个阶段:
①至分钟,小刚从家走到菜地;
②至分钟,小刚在菜地浇水;
③至分钟,小刚从菜地走到青稞地;
④至分钟,小刚在青稞地除草;
⑤至分钟,小刚从青稞地回到家;
综合上面的分析得:由③的过程知,(千米);
由②、④的过程知(分钟).
故答案为:,.
【点睛】本题考查了利用函数的图象获取信息、有理数的加减法,正确理解函数图象横纵坐标表示的意义是解题关键.
15.4
【详解】解:由图可知,甲、乙收割机每天共收割350-200=150亩,共同收割600亩,
所以,乙参与收割的天数是600÷150=4天.
故答案为4.
【点睛】此题主要考查学生的读图获取信息的能力,要注意分析其中的“关键点”.
16.
【分析】根据函数图像,结合题意分析分别求得进水速度和出水速度,即可求解.
【详解】解:依题意,3分钟进水30升,则进水速度为升/分钟,
3分钟时,再打开出水管排水,8分钟时,关闭进水管,直至容器中的水全部排完直至容器中的水全部排完,
则排水速度为升/分钟,
,
解得.
故答案为:.
【点睛】本题考查了函数图象问题,从函数图象获取信息是解题的关键.
17.
【分析】根据图象可得沙漏漏沙的速度,从而得出从开始计时到沙子漏光所需的时间.
【详解】解:沙漏漏沙的速度为:(克/小时),
∴从开始计时到沙子漏光所需的时间为:(小时).
故答案为:.
【点睛】】
【点评】本题考查了函数图象的应用,学会看函数图象,理解函数图象所反映的实际意义,从函数图象中获取信息,并且解决有关问题.
18.(1)如图所示见解析,4:3;(2)b的值为4;(3)乙车的速度为80km/h.
【分析】(1)利用图象与x轴的交点坐标得出AC,BC的长,进而得出答案;
(2)利用甲车行驶的距离与时间求出平均速度即可,进而得出b的值;
(3)利用甲的速度得出3小时乙行驶的距离进而得出他的速度.
【详解】(1)如图所示,
由题意结合图象的纵坐标得出:甲地到C地距离为:240km,乙地到C地距离为:180km,
∴AC=240,BC=180,
∴AC:BC的值为:4:3;
(2)∵由图象可得出:甲车420km一共行驶7小时,
∴420÷7=60(km/h),
240÷60=4,
故b的值为4;
(3)∵甲的速度为60km/h,
∴3小时甲行驶了180km,此时距C地60km,
∴此时乙已经行驶了:180+60=240(km),
∴乙的速度为:240÷3=80(km/h).
故答案为(1)如图所示见解析,4:3;(2)b的值为4;(3)乙车的速度为80km/h.
【点睛】本题考查函数的图象,自变量和函数值,解题的关键是从函数的图像获取路程时间等重要信息.
19.(1)甲;甲;;或
(2)
【分析】(1)根据图象直接填写即可;根据图象中两函数图象交点即为甲、乙生产的零件个数相等时的信息.
(2)根据图象即可得到生产速度最快的时间段,再根据题意即可求出最快的速度.
【详解】(1)由图象可知,甲先完成一天的生产任务在生产过程中,甲因机器故障停止生产小时
由图象可知,
当或时,两函数图象相交,即为甲、乙生产的零件个数相等
故为3或5.5时,甲、乙生产的零件个数相等.
(2)由图象可知甲在时内倾斜角度最大,生产速度快;
此时甲每小时生产零件的个数为(个).
【点睛】本题考查了从图象中获取信息,解题的关键是根据题意得到相关的信息.
20.(1)甲生产线生产时对应的函数关系式是;乙生产线生产时对应的函数关系式为
(2)第10天结束时,甲生产线的总产量高;第30天结束时,乙生产线的总产量高
【分析】(1)根据甲生产线已生产了200吨成品后,乙生产线开始投入生产,甲、乙两条生产线每天分别生产20吨和30吨成品列出对应的函数关系式即可;
(2)根据(1)所求,先求出两条生产线产量相同是在第几天,然后画出函数图象,观察函数图象即可得到答案.
【详解】(1)解:由题意可得:甲生产线生产时对应的函数关系式是;
乙生产线生产时对应的函数关系式为.
(2)令,解得,可知在第20天结束时,两条生产线的产量相同,
故甲生产线所对应的生产函数图象一定经过点(0,200)和(20,600);
乙生产线所对应的生产函数图象一定经过点(0,0)和(20,600).
作出图象如图所示.
由图象可知:第10天结束时,甲生产线的总产量高;第30天结束时,乙生产线的总产量高.
【点睛】本题主要考查了列函数关系式,从函数图象获取信息,正确理解题意列出函数关系式是解题的关键.
21.(1)2,4,276
(2)828千米
【分析】(1)根据函数图像中的数据,可以写出快车比慢车晚几小时出发,快车比慢车早到几小时,快车追上慢车时,快车行驶了多少千米;
(2)根据图像中的数据,可以计算出慢车的速度,然后根据路程=速度×时间,即可计算出A、B两地相距多少千米.
【详解】(1)解:由图像可得,
慢车比快车晚2小时出发,快车比慢车早到18﹣14=4(小时),快车追上慢车时,快行驶了276千米,
故答案为:2,4,276;
(2)解:由图像可得,
慢车的速度为:276÷6=46(千米/时),
46×18=828(千米),
答:A、B两地相距828千米.
【点睛】本题考查一次函数的应用,利用数形结合的思想解答是解答本题的关键.
22.见解析
【详解】试题分析:
(1)(3)观察、分析图象中的数据信息,结合题意即可得到相应答案;
(4)图中的横线表示人的正常体温:37℃;
(5)由图象可知,这位病人的体温逐渐趋近于正常体温,由此可知病人的病情在好转.
试题解析:
(1)观察图象可得:护士每隔6小时给病人测量一次体温;
(2)观察图象可得:这位病人的最高体温是39.5℃,最低体温是36.8℃;
(3)这位病人4月8日12时的体温是37.5℃;
(4)图中的横线表示人的正常体温是37℃;
(5)从图象的变化趋势看可以看出,这位病人的体温逐渐趋近于正常体温,
∴这位病人的病情在好转.
23.(1)t;s;(2)小于;(3)乙追赶上了甲;(4)9;4.5;(5)后面;(6)不对.
【分析】(1)根据自变量与因变量的含义得到时间是自变量,路程是因变量;
(2)甲走6小时行驶100千米,乙走3小时走100千米,则可得到他们的速度的大小;
(3)6时两图象相交,说明他们相遇;
(4)观察图象直接得到答案;
(5)观察图象观察得到;
(6)观察图象得到甲先出发3小时后,乙才开始出发.
【详解】解:(1)函数图象反映路程随时间变化的图象,则t是自变量,s是因变量;
故答案为:t,s;
(2)甲的速度是100÷6=千米/小时,乙的速度是100÷3=千米/小时,所以甲的速度小于乙的速度;
故答案为:小于;
(3)6时表示他们相遇,即乙追赶上了甲;
故答案为:乙追赶上了甲;
(4)路程为150千米,甲行驶9小时,乙行驶了7.5-3=4.5小时;
故答案为:9,4.5;
(5)t=9时,乙的图象在甲的上方,即乙行驶的路程远些,所以9时甲在乙的后面;
故答案为:后面;
(6)不对,是乙比甲晚走了3小时.
故答案为:不对.
24.(1)
(2)
(3)
【分析】(1)由函数图象可知小雪跑步5分钟的路程为米,即可根据路程速度时间求出答案;
(2)先求出小雪步行的速度,然后设小雪在第t分钟改为步行,根据小雪第分钟到达图书馆建立方程求出t的值,再由函数图象可知小雪改为步行时两人相距求出小松骑车的速度即可;
(3)先求出小松到家的时间,再根据路程速度时间求出答案即可.
【详解】(1)解:由函数图象可知小雪跑步5分钟的路程为,
∴小雪跑步的速度为;
(2)解:由(1)得小雪步行的速度为,
设小雪在第t分钟改为步行,
∴,
解得,
∴由函数图象可知,当第10分钟时,小雪改为步行,此时两人相距,
∴小松骑车的速度为;
(3)解:由(2)得小松到家的时间为,
∴小雪离图书馆的距离为.
【点睛】本题主要考查了从函数图象获取信息,一元一次方程的实际应用,正确读懂函数图象是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
