24.3基本几何体的平面展开图同步练习(含解析)
文档属性
| 名称 | 24.3基本几何体的平面展开图同步练习(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 703.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 21:25:15 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
24.3基本几何体的平面展开图
学校:___________姓名:___________班级:___________考号:___________
一、单选题
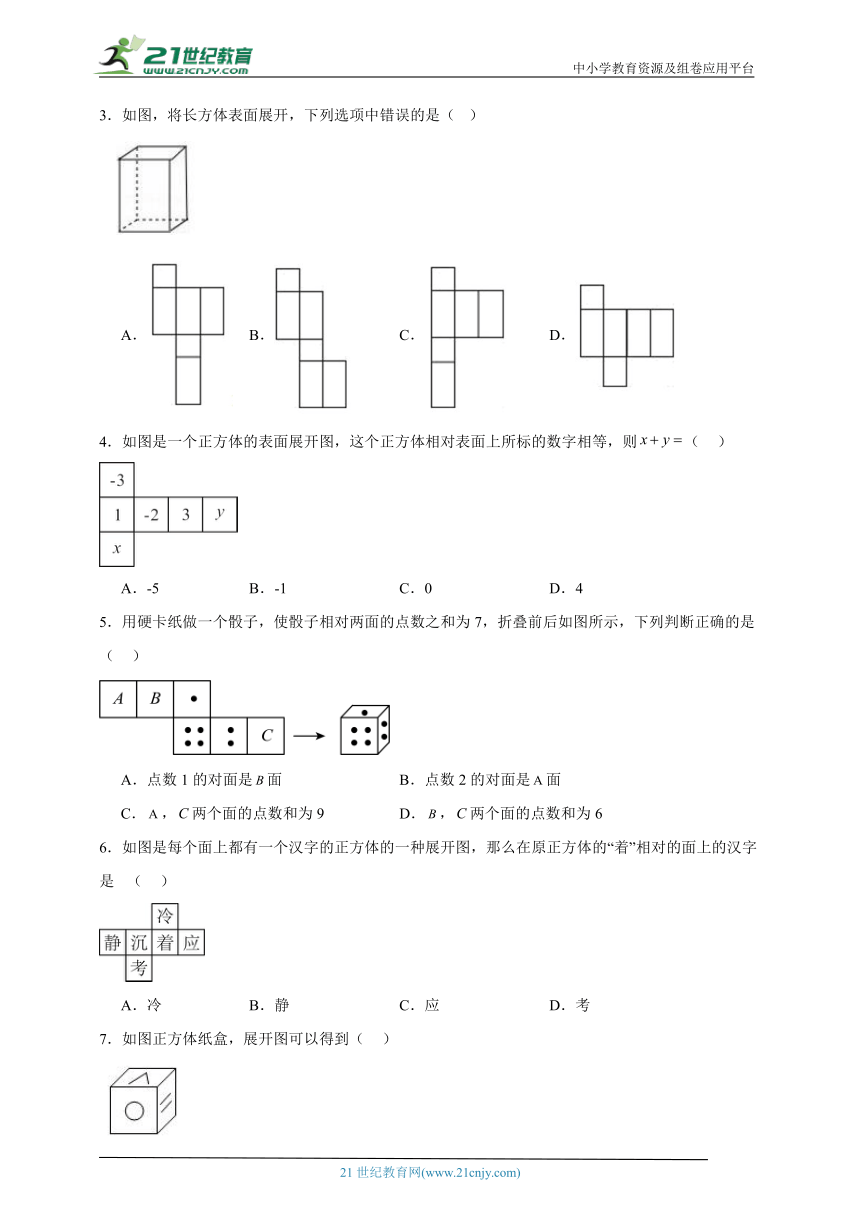
1.如图所示的平面图形,哪个不是立方体的展开图( )
A. B.
C. D.
2.如图,每个图片都是6个相同的正方形组成的,不能折成正方体的是( ).
A. B. C. D.
3.如图,将长方体表面展开,下列选项中错误的是( )
A. B. C. D.
4.如图是一个正方体的表面展开图,这个正方体相对表面上所标的数字相等,则( )
A.-5 B.-1 C.0 D.4
5.用硬卡纸做一个骰子,使骰子相对两面的点数之和为7,折叠前后如图所示,下列判断正确的是( )
A.点数1的对面是面 B.点数2的对面是面
C.,两个面的点数和为9 D.,两个面的点数和为6
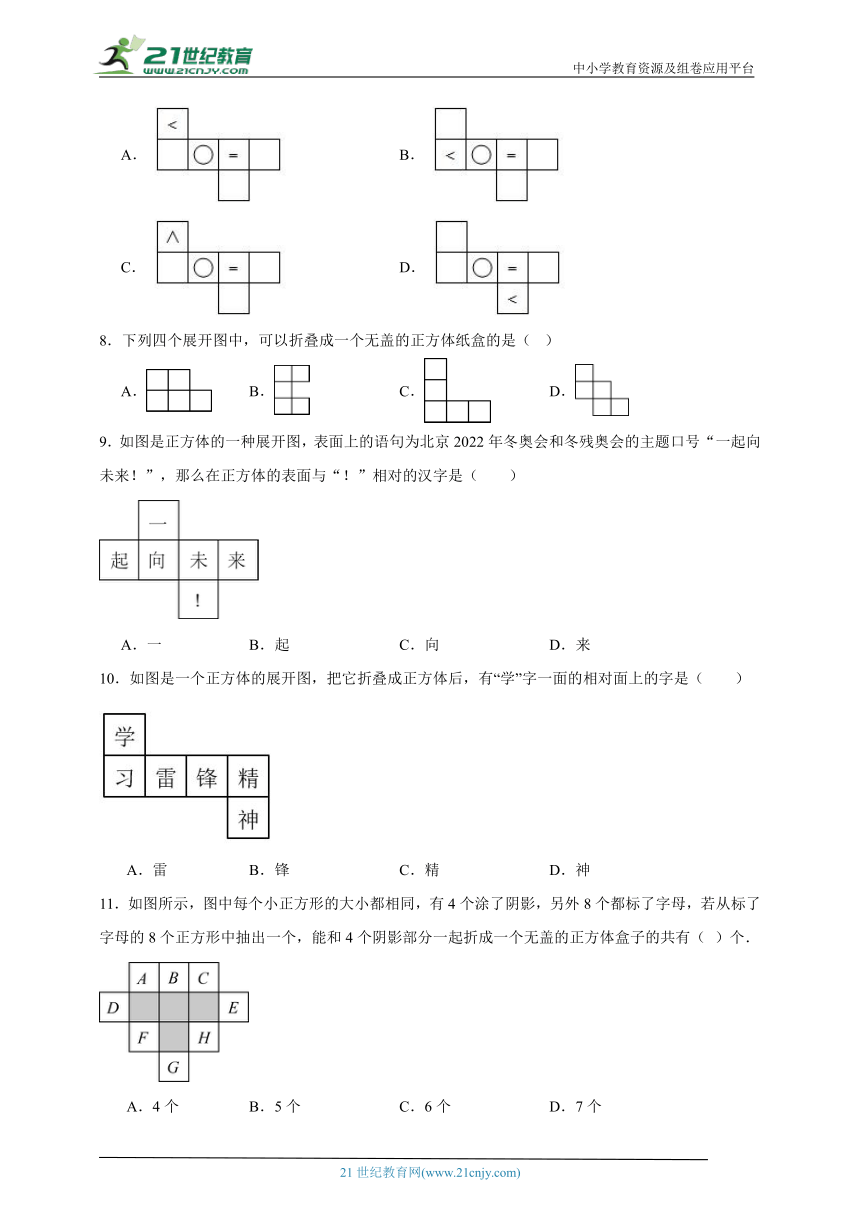
6.如图是每个面上都有一个汉字的正方体的一种展开图,那么在原正方体的“着”相对的面上的汉字是 ( )
A.冷 B.静 C.应 D.考
7.如图正方体纸盒,展开图可以得到( )
A. B.
C. D.
8.下列四个展开图中,可以折叠成一个无盖的正方体纸盒的是( )
A. B. C. D.
9.如图是正方体的一种展开图,表面上的语句为北京2022年冬奥会和冬残奥会的主题口号“一起向未来!”,那么在正方体的表面与“!”相对的汉字是( )
A.一 B.起 C.向 D.来
10.如图是一个正方体的展开图,把它折叠成正方体后,有“学”字一面的相对面上的字是( )
A.雷 B.锋 C.精 D.神
11.如图所示,图中每个小正方形的大小都相同,有4个涂了阴影,另外8个都标了字母,若从标了字母的8个正方形中抽出一个,能和4个阴影部分一起折成一个无盖的正方体盒子的共有( )个.
A.4个 B.5个 C.6个 D.7个
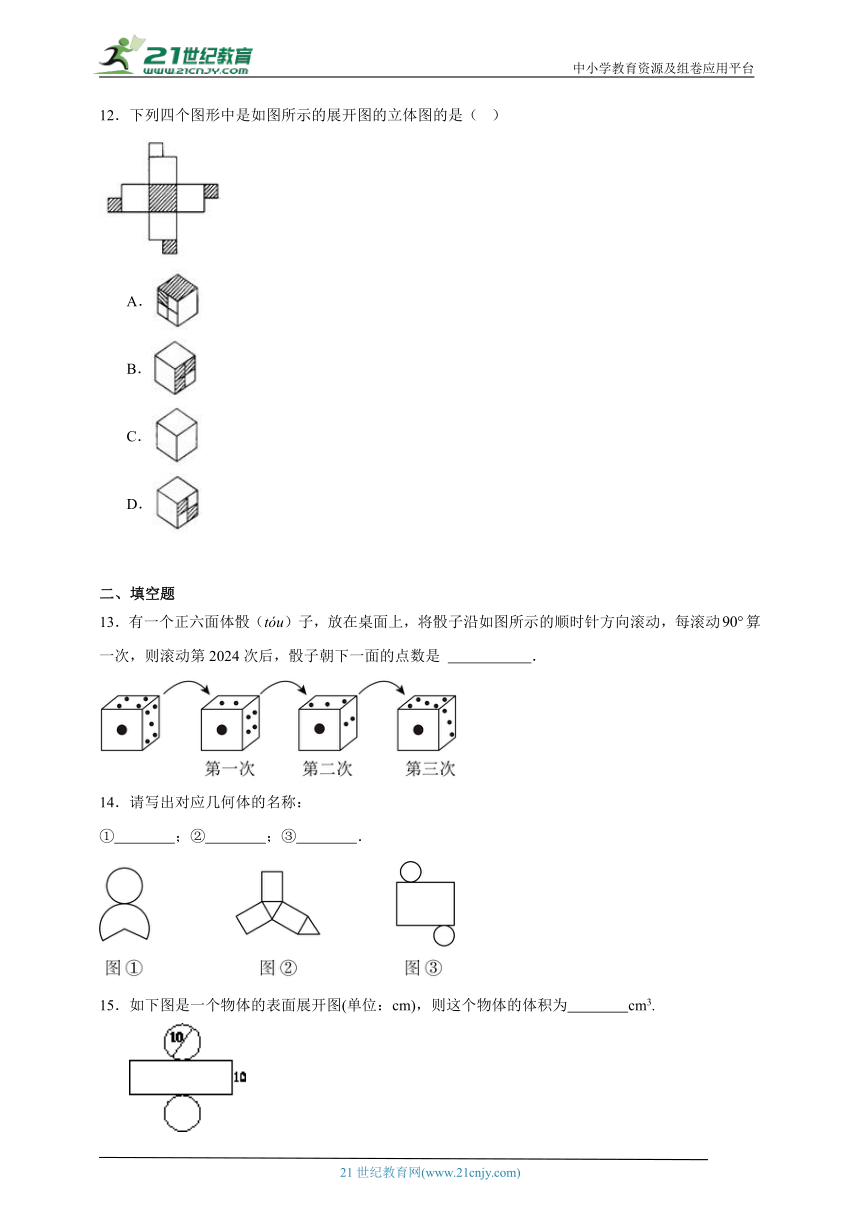
12.下列四个图形中是如图所示的展开图的立体图的是( )
A.
B.
C.
D.
二、填空题
13.有一个正六面体骰(tóu)子,放在桌面上,将骰子沿如图所示的顺时针方向滚动,每滚动算一次,则滚动第2024次后,骰子朝下一面的点数是 .
14.请写出对应几何体的名称:
① ;② ;③ .
15.如下图是一个物体的表面展开图(单位:cm),则这个物体的体积为 cm3.
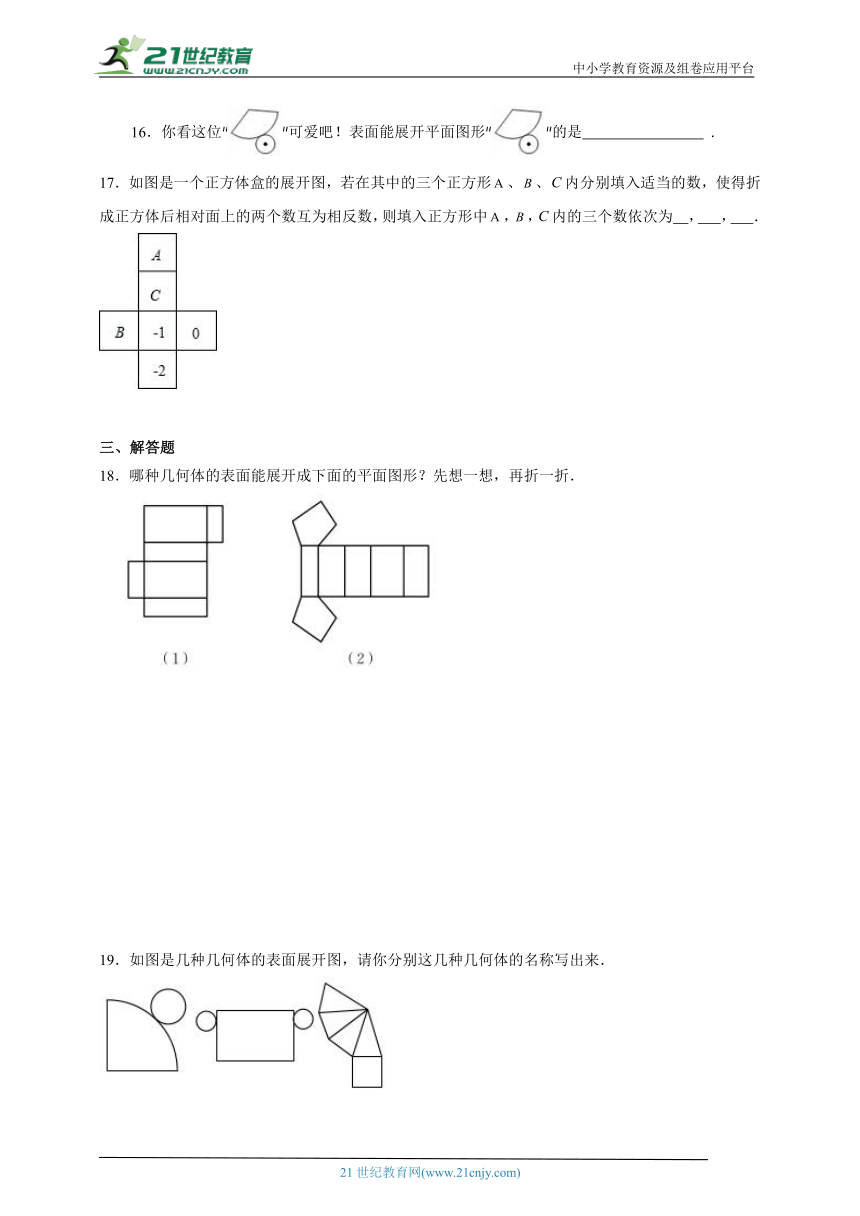
16.你看这位""可爱吧!表面能展开平面图形""的是 .
17.如图是一个正方体盒的展开图,若在其中的三个正方形、、内分别填入适当的数,使得折成正方体后相对面上的两个数互为相反数,则填入正方形中,,内的三个数依次为 , , .
三、解答题
18.哪种几何体的表面能展开成下面的平面图形?先想一想,再折一折.
19.如图是几种几何体的表面展开图,请你分别这几种几何体的名称写出来.
20.已知一个直棱柱有8个面,它的底面边长都是5cm,侧棱长都是4cm.
(1)它是几棱柱?它有多少个顶点?多少条棱?
(2)这个棱柱的所有侧面的面积之和是多少?
21.小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
(1)小明总共剪开了______条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.
(3)小明说:已知这个长方体纸盒高为, 底面是一个正方形,并且这个长方体纸盒所有棱长的和是, 求这个长方体纸盒的体积及表面积.
22.一个正方体的展开图已有一部分(如图),还有一个正方形未画,现有10个位置可供选择,请问:放在哪些位置能围成正方体,放在哪些位置不能围成正方体?
23.【问题情境】
数学综合与实践活动课上,老师提出如下问题:一个三级台阶,它每一级的长、宽、高分别为20、3、2,和是一个台阶两个相对的端点.
【探究实践】
老师让同学们探究:如图①,若点处有一只蚂蚁要到点去吃可口的食物,那么蚂蚁沿着台阶爬到点的最短路程是多少?
(1)同学们经过思考得到如下解题方法:如图②,将三级台阶展开成平面图形,可得到长为20.宽为15的长方形,连接,经过计算得到长度为___________,就是最短路程.
【变式探究】
(2)如图③,是一只圆柱形玻璃杯,该玻璃杯的底面周长是,高是,若蚂蚁从点出发沿着玻璃杯的侧面到点,则蚂蚁爬行的最短距离为___________.-
【拓展应用】
(3)如图④,圆柱形玻璃杯的高,底面周长为,在杯内壁离杯底的点处有一滴蜂蜜,此时,一只蚂蚁正好在外壁上,离杯上沿,且与蜂蜜相对的点处,则蚂蚁从外壁处到内壁处所爬行的最短路程是多少?(杯壁厚度不计)(画出示意图并进行计算)
24.如图,方格纸中每个小正方形的边长均为1.
(1)观察图①②中所画的“”形图形,然后各补画一个小正方形,使图①中所得到的图形是轴对称图形,图②中所得到的图形是中心对称图形;
(2)补画后,图①②中所得到的图形是不是正方体的展开图?
《24.3基本几何体的平面展开图》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D A C A C B A D A D
题号 11 12
答案 C B
1.D
【解析】略
2.A
【分析】根据正方体展开图的类型有1-4-1型,2-3-1型,2-2-2型,3-3型,即可判断.
【详解】解:A、不属于其中任何的类型,不能折成正方体,故本选项符合题意;
B、属于正方体展开图的类型2-3-1型,能折成正方体,故本选项不符合题意;
C、属于正方体展开图的类型1-4-1型,能折成正方体,故本选项不符合题意;
D、属于正方体展开图的类型2-2-2型,能折成正方体,故本选项不符合题意;
故选:A.
【点睛】此题考查正方体的展开图,解决此题的关键是熟练掌握正方体展开图的类型1-4-1型,2-3-1型,2-2-2型,3-3型.
3.C
【分析】根据长方体的展开图即可判断.
【详解】A、是长方体平面展开图,不符合题意;
B、是长方体平面展开图,不符合题意;
C、有两个面重合,不是长方体平面展开图,不符合题意;
D、是长方体平面展开图,不符合题意.
故选C.
4.A
【分析】利用正方体及其表面展开图的特点解题.
【详解】解:这是一个正方体的平面展开图,共有六个面,其中面“x”与面“-3”相对,面“y”与面“-2”相对,“3”与面“1”相对.
正方体的相对表面上所标的数字相等,
x=-3, y=-2
x+y=-3+(-2) =-5.
故选:A.
【点睛】本题考查了正方体相对两个面上的文字,掌握找正方体相对两个面上的文字的方法,注意正方体的空间图形,从相对面入手,分析解答问题是解题的关键.
5.C
【分析】本题考查正方体展开图的相对面,根据同行隔一个,确定出相对面,再进行判断即可.
【详解】解:由图可知:点数1的对面是面,故的点数为;
点数的对面是面,故的点数为;
点数的对面是面,故的点数为,
∴,两个面的点数和为9,,两个面的点数和为8;
故选C.
6.B
【分析】利用正方体及其表面展开图的特点解题.
【详解】这是一个正方体的平面展开图,共有六个面,其中面“静”与面“着”相对,面“沉”与面“应”相对,“冷”与面“考”相对.
故选:B.
7.A
【分析】根据折叠后圆、等于符号及小于符号所在的面的位置进行判断即可.
【详解】解:A.圆、等于符号及小于符号所在的面折叠后互为邻面,且小于符号的开口与等于符号开口一致,符合题意;
B.小于符号与等于符号的面折叠后是对面,不符合题意;
C.折叠后,小于符号的开口方向与等于符号开口方向不同,不符合题意;
D.折叠后,小于符号开口没有指向圆,不符合题意.
故答案选A.
【点睛】本题考查了正方体的展开图,熟练掌握正方体的展开图,明白对面相隔不相邻这一原则以及正确区分折叠后图形的相对位置是解题的关键.
8.D
【分析】根据正方体11种展开图,添上1个小正方形,是正方体11种展开图的可以折叠成一个无盖的正方体盒子,据此分析, 关键是具有一定的空间想象能力,掌握正方体11种展开图.
【详解】解:A、无法折叠成正方体,故不符合题意;
B、有一个面会重叠,故不符合题意;
C、有一个面会重叠,不符合题意;
D、可以折叠成一个无盖的正方体盒子,符合题意,
故选:D.
9.A
【分析】由平面图形的折叠及立体图形的表面展开图的特点解题.
【详解】解:对于正方体的平面展开图中相对的面一定相隔一个小正方形,由图形可知,与“!”字相对的字是“一”.
故选:A.
【点睛】本题考查生活中的立体图形与平面图形,注意正方体的空间图形,从相对面入手,分析及解答问题.
10.D
【分析】根据正方体的表面展开图的特征,判断相对的面即可.
【详解】解:由正方体的表面展开图的特征可知:
“学”的对面是“神”,
故选:D.
【点睛】本题考查了正方体相对两个面上的文字,掌握正方体表面展开图的特征是正确判断的关键.
11.C
【分析】由平面图形的折叠及正方体的展开图解题即可.
【详解】解:从标了字母的8个正方形中抽出一个,能和4个阴影部分一起折成一个无盖的正方体盒子的字母有:A、B、C、D、E、G,共有6个,
故选:C.
【点睛】本题考查了展开图折叠成几何体的知识,解题时勿忘记四棱柱的特征及正方体展开图的各种情形.
12.B
【详解】由展开图可知含小黑正方形的面不能与含大黑正方形的面相邻,所以A,C不是展开图所对应的立体图;折叠后三个小黑正方形在同一面,这样D不符合;在A图中,正好是大黑正方形在上面,那么含小黑正方形就在底面,B符合;
故选B.
13.3
【分析】本题考查了正方体相对两个面上的文字及图形的变化类问题,解题的关键是发现规律.观察图形知道点数三和点数四相对,点数二和点数五相对且四次一循环,从而确定答案.
【详解】解:观察图形知道点数三和点数四相对,点数二和点数五相对且四次一循环,
∵,
∴滚动第2024次后与开始滚动时相同,
∴朝下的数字是4的对面3,
故答案为:3.
14. 圆锥 三棱柱 圆柱
【分析】根据常见几何体的展开图注意判断即可.
【详解】
中依次是圆锥,三棱柱,圆柱,
故答案为:圆锥,三棱柱,圆柱.
【点睛】本题考查了常见几何体的展开图,熟练掌握几何体的展开图是解题的关键.
15.250π.
【详解】【分析】根据:体积=底面积×高可得.
【详解】底面面积是: =25cm2,
所以物体体积是: 25×10=250πcm3.
故答案为250π.:
【点睛】本题考核知识点:求几何体的体积.解题关键点:记住体积公式.
16.圆锥
【详解】根据圆锥的侧面展开图是扇形,底面是圆形,可得圆锥的展开图是“”,
故答案为圆锥.
17. 1 0 2
【分析】利用正方体及其表面展开图的特点解题.
【详解】解:由于只有符号不同的两个数互为相反数,由正方体的展开图解题得填入正方形中,,内的三个数依次为1,0,2.
故答案为1,0,2
【点睛】本题主要考查互为相反数的概念,只有符号不同的两个数互为相反数.解题时勿忘记正方体展开图的各种情形.
18.(1)长方体;(2)五棱柱
【分析】分别利用已知平面展开图进而分析得出答案.
【详解】解:如图(1)可以折成长方体,
如图(2)可以折成五棱柱.
【点睛】本题主要考查展开图折叠成几何体的知识点,熟记常见立体图形的平面展开图是解决此类问题的关键.
19.圆锥;圆柱;四棱锥
【解析】略
20.(1)它是六棱柱,它有12个顶点,18条棱;
(2)这个棱柱的所有侧面的面积之和是120
【分析】(1)根据棱柱面、顶点、棱之间的关系得出答案;
(2)计算侧面面积即可.
【详解】(1)解:因为一个直棱柱有8个面,所以它是六棱柱,
所以有12个顶点,18条棱,
答:它是六棱柱,它有12个顶点,18条棱;
(2)因为六棱柱的底面边长都是5cm,侧棱长都是4cm,
所以侧面展开后是长为5×6=30cm,宽为4cm的长方形,
因此侧面积为30×4=120(cm2),
答:这个棱柱的所有侧面的面积之和是120.
【点睛】此题考查了棱柱的面、顶点、棱之间的关系,计算侧面展开图的面积,正确掌握直棱柱的特点是解题的关键.
21.(1)8
(2)见解析
(3)这个长方体纸盒的体积为立方厘米,表面积为 平方厘米.
【分析】(1)根据长方体总共有12条棱,有4条棱未剪开,即可得出剪开的棱的条数;
(2)根据长方体的展开图的情况可知有4种情况;
(3)设底面边长为,根据棱长的和是,列出方程可求出底面边长,进而得到长方体纸盒的体积和表面积.
【详解】(1)解:由图可得,小明共剪了8条棱,
故答案为:8.
(2)如图,粘贴的位置有四种情况如下:
(3)∵长方体纸盒的底面是一个正方形,
∴可设底面边长,
∵长方体纸盒所有棱长的和是,长方体纸盒高为,
∴,
解得,
∴这个长方体纸盒的体积为:立方厘米.
这个长方体纸盒的表面积为:平方厘米.
【点睛】本题主要考查了几何展开图,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念,是解决此类问题的关键.
22.放在①⑦⑧⑨可围成正方体;放在②③④⑤⑥⑩不可以围成正方体.
【详解】【分析】先把已知的展开图折回,漏的空就是①⑦⑧⑨四边围成的正方形,所以只能放在这四个位置.
【详解】解:
放在①⑦⑧⑨可围成正方体;
放在②③④⑤⑥⑩不可以围成正方体.
【点睛】本题考核知识点:展开图与立体图形. 解题关键点:动手把展开图折回立体图形进行分析.
23.(1)(2)(3)
【分析】本题考查了平面展开图—最短路径问题,解答本题的关键是熟练运用数形结合的思想解决问题.
(1)直接利用勾股定理进行求解即可;
(2)将圆柱体展开,利用勾股定理求解即可;
(3)从玻璃杯侧面展开,作关于的对称点,根据两点之间线段最短可知的长度即为所求,利用勾股定理求解即可.
【详解】解:(1)由题意得,
故答案为:;
(2)将圆柱体展开,由题意得
,
故答案为:;
(3)如图,
从玻璃杯侧面展开,作关于的对称点,作交延长线于点,连接交于点,
,,
,
,
,
蚂蚁从外壁处到内壁处所爬行的最短路程是.
24.(1)作图见解析
(2)图①左不是正方体的展开图,图①右是正方体的展开图,图②是正方体的展开图.
【分析】(1)根据轴对称及中心对称图形的定义作图即可得到答案;
(2)由正方体的平面展开图验证即可判断.
【详解】(1)解:如图所示(所画轴对称图形不唯一):
图①是轴对称图形,图②是中心对称图形;
(2)解:由(1)中图形可知,图①左不是正方体的展开图,图①右是正方体的展开图,图②是正方体的展开图.
【点睛】本题考查中心对称图形与轴对称图形的定义、正方体的平面展开图等知识,熟练掌握中心对称图形与轴对称图形的定义是解决问题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
24.3基本几何体的平面展开图
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图所示的平面图形,哪个不是立方体的展开图( )
A. B.
C. D.
2.如图,每个图片都是6个相同的正方形组成的,不能折成正方体的是( ).
A. B. C. D.
3.如图,将长方体表面展开,下列选项中错误的是( )
A. B. C. D.
4.如图是一个正方体的表面展开图,这个正方体相对表面上所标的数字相等,则( )
A.-5 B.-1 C.0 D.4
5.用硬卡纸做一个骰子,使骰子相对两面的点数之和为7,折叠前后如图所示,下列判断正确的是( )
A.点数1的对面是面 B.点数2的对面是面
C.,两个面的点数和为9 D.,两个面的点数和为6
6.如图是每个面上都有一个汉字的正方体的一种展开图,那么在原正方体的“着”相对的面上的汉字是 ( )
A.冷 B.静 C.应 D.考
7.如图正方体纸盒,展开图可以得到( )
A. B.
C. D.
8.下列四个展开图中,可以折叠成一个无盖的正方体纸盒的是( )
A. B. C. D.
9.如图是正方体的一种展开图,表面上的语句为北京2022年冬奥会和冬残奥会的主题口号“一起向未来!”,那么在正方体的表面与“!”相对的汉字是( )
A.一 B.起 C.向 D.来
10.如图是一个正方体的展开图,把它折叠成正方体后,有“学”字一面的相对面上的字是( )
A.雷 B.锋 C.精 D.神
11.如图所示,图中每个小正方形的大小都相同,有4个涂了阴影,另外8个都标了字母,若从标了字母的8个正方形中抽出一个,能和4个阴影部分一起折成一个无盖的正方体盒子的共有( )个.
A.4个 B.5个 C.6个 D.7个
12.下列四个图形中是如图所示的展开图的立体图的是( )
A.
B.
C.
D.
二、填空题
13.有一个正六面体骰(tóu)子,放在桌面上,将骰子沿如图所示的顺时针方向滚动,每滚动算一次,则滚动第2024次后,骰子朝下一面的点数是 .
14.请写出对应几何体的名称:
① ;② ;③ .
15.如下图是一个物体的表面展开图(单位:cm),则这个物体的体积为 cm3.
16.你看这位""可爱吧!表面能展开平面图形""的是 .
17.如图是一个正方体盒的展开图,若在其中的三个正方形、、内分别填入适当的数,使得折成正方体后相对面上的两个数互为相反数,则填入正方形中,,内的三个数依次为 , , .
三、解答题
18.哪种几何体的表面能展开成下面的平面图形?先想一想,再折一折.
19.如图是几种几何体的表面展开图,请你分别这几种几何体的名称写出来.
20.已知一个直棱柱有8个面,它的底面边长都是5cm,侧棱长都是4cm.
(1)它是几棱柱?它有多少个顶点?多少条棱?
(2)这个棱柱的所有侧面的面积之和是多少?
21.小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
(1)小明总共剪开了______条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.
(3)小明说:已知这个长方体纸盒高为, 底面是一个正方形,并且这个长方体纸盒所有棱长的和是, 求这个长方体纸盒的体积及表面积.
22.一个正方体的展开图已有一部分(如图),还有一个正方形未画,现有10个位置可供选择,请问:放在哪些位置能围成正方体,放在哪些位置不能围成正方体?
23.【问题情境】
数学综合与实践活动课上,老师提出如下问题:一个三级台阶,它每一级的长、宽、高分别为20、3、2,和是一个台阶两个相对的端点.
【探究实践】
老师让同学们探究:如图①,若点处有一只蚂蚁要到点去吃可口的食物,那么蚂蚁沿着台阶爬到点的最短路程是多少?
(1)同学们经过思考得到如下解题方法:如图②,将三级台阶展开成平面图形,可得到长为20.宽为15的长方形,连接,经过计算得到长度为___________,就是最短路程.
【变式探究】
(2)如图③,是一只圆柱形玻璃杯,该玻璃杯的底面周长是,高是,若蚂蚁从点出发沿着玻璃杯的侧面到点,则蚂蚁爬行的最短距离为___________.-
【拓展应用】
(3)如图④,圆柱形玻璃杯的高,底面周长为,在杯内壁离杯底的点处有一滴蜂蜜,此时,一只蚂蚁正好在外壁上,离杯上沿,且与蜂蜜相对的点处,则蚂蚁从外壁处到内壁处所爬行的最短路程是多少?(杯壁厚度不计)(画出示意图并进行计算)
24.如图,方格纸中每个小正方形的边长均为1.
(1)观察图①②中所画的“”形图形,然后各补画一个小正方形,使图①中所得到的图形是轴对称图形,图②中所得到的图形是中心对称图形;
(2)补画后,图①②中所得到的图形是不是正方体的展开图?
《24.3基本几何体的平面展开图》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D A C A C B A D A D
题号 11 12
答案 C B
1.D
【解析】略
2.A
【分析】根据正方体展开图的类型有1-4-1型,2-3-1型,2-2-2型,3-3型,即可判断.
【详解】解:A、不属于其中任何的类型,不能折成正方体,故本选项符合题意;
B、属于正方体展开图的类型2-3-1型,能折成正方体,故本选项不符合题意;
C、属于正方体展开图的类型1-4-1型,能折成正方体,故本选项不符合题意;
D、属于正方体展开图的类型2-2-2型,能折成正方体,故本选项不符合题意;
故选:A.
【点睛】此题考查正方体的展开图,解决此题的关键是熟练掌握正方体展开图的类型1-4-1型,2-3-1型,2-2-2型,3-3型.
3.C
【分析】根据长方体的展开图即可判断.
【详解】A、是长方体平面展开图,不符合题意;
B、是长方体平面展开图,不符合题意;
C、有两个面重合,不是长方体平面展开图,不符合题意;
D、是长方体平面展开图,不符合题意.
故选C.
4.A
【分析】利用正方体及其表面展开图的特点解题.
【详解】解:这是一个正方体的平面展开图,共有六个面,其中面“x”与面“-3”相对,面“y”与面“-2”相对,“3”与面“1”相对.
正方体的相对表面上所标的数字相等,
x=-3, y=-2
x+y=-3+(-2) =-5.
故选:A.
【点睛】本题考查了正方体相对两个面上的文字,掌握找正方体相对两个面上的文字的方法,注意正方体的空间图形,从相对面入手,分析解答问题是解题的关键.
5.C
【分析】本题考查正方体展开图的相对面,根据同行隔一个,确定出相对面,再进行判断即可.
【详解】解:由图可知:点数1的对面是面,故的点数为;
点数的对面是面,故的点数为;
点数的对面是面,故的点数为,
∴,两个面的点数和为9,,两个面的点数和为8;
故选C.
6.B
【分析】利用正方体及其表面展开图的特点解题.
【详解】这是一个正方体的平面展开图,共有六个面,其中面“静”与面“着”相对,面“沉”与面“应”相对,“冷”与面“考”相对.
故选:B.
7.A
【分析】根据折叠后圆、等于符号及小于符号所在的面的位置进行判断即可.
【详解】解:A.圆、等于符号及小于符号所在的面折叠后互为邻面,且小于符号的开口与等于符号开口一致,符合题意;
B.小于符号与等于符号的面折叠后是对面,不符合题意;
C.折叠后,小于符号的开口方向与等于符号开口方向不同,不符合题意;
D.折叠后,小于符号开口没有指向圆,不符合题意.
故答案选A.
【点睛】本题考查了正方体的展开图,熟练掌握正方体的展开图,明白对面相隔不相邻这一原则以及正确区分折叠后图形的相对位置是解题的关键.
8.D
【分析】根据正方体11种展开图,添上1个小正方形,是正方体11种展开图的可以折叠成一个无盖的正方体盒子,据此分析, 关键是具有一定的空间想象能力,掌握正方体11种展开图.
【详解】解:A、无法折叠成正方体,故不符合题意;
B、有一个面会重叠,故不符合题意;
C、有一个面会重叠,不符合题意;
D、可以折叠成一个无盖的正方体盒子,符合题意,
故选:D.
9.A
【分析】由平面图形的折叠及立体图形的表面展开图的特点解题.
【详解】解:对于正方体的平面展开图中相对的面一定相隔一个小正方形,由图形可知,与“!”字相对的字是“一”.
故选:A.
【点睛】本题考查生活中的立体图形与平面图形,注意正方体的空间图形,从相对面入手,分析及解答问题.
10.D
【分析】根据正方体的表面展开图的特征,判断相对的面即可.
【详解】解:由正方体的表面展开图的特征可知:
“学”的对面是“神”,
故选:D.
【点睛】本题考查了正方体相对两个面上的文字,掌握正方体表面展开图的特征是正确判断的关键.
11.C
【分析】由平面图形的折叠及正方体的展开图解题即可.
【详解】解:从标了字母的8个正方形中抽出一个,能和4个阴影部分一起折成一个无盖的正方体盒子的字母有:A、B、C、D、E、G,共有6个,
故选:C.
【点睛】本题考查了展开图折叠成几何体的知识,解题时勿忘记四棱柱的特征及正方体展开图的各种情形.
12.B
【详解】由展开图可知含小黑正方形的面不能与含大黑正方形的面相邻,所以A,C不是展开图所对应的立体图;折叠后三个小黑正方形在同一面,这样D不符合;在A图中,正好是大黑正方形在上面,那么含小黑正方形就在底面,B符合;
故选B.
13.3
【分析】本题考查了正方体相对两个面上的文字及图形的变化类问题,解题的关键是发现规律.观察图形知道点数三和点数四相对,点数二和点数五相对且四次一循环,从而确定答案.
【详解】解:观察图形知道点数三和点数四相对,点数二和点数五相对且四次一循环,
∵,
∴滚动第2024次后与开始滚动时相同,
∴朝下的数字是4的对面3,
故答案为:3.
14. 圆锥 三棱柱 圆柱
【分析】根据常见几何体的展开图注意判断即可.
【详解】
中依次是圆锥,三棱柱,圆柱,
故答案为:圆锥,三棱柱,圆柱.
【点睛】本题考查了常见几何体的展开图,熟练掌握几何体的展开图是解题的关键.
15.250π.
【详解】【分析】根据:体积=底面积×高可得.
【详解】底面面积是: =25cm2,
所以物体体积是: 25×10=250πcm3.
故答案为250π.:
【点睛】本题考核知识点:求几何体的体积.解题关键点:记住体积公式.
16.圆锥
【详解】根据圆锥的侧面展开图是扇形,底面是圆形,可得圆锥的展开图是“”,
故答案为圆锥.
17. 1 0 2
【分析】利用正方体及其表面展开图的特点解题.
【详解】解:由于只有符号不同的两个数互为相反数,由正方体的展开图解题得填入正方形中,,内的三个数依次为1,0,2.
故答案为1,0,2
【点睛】本题主要考查互为相反数的概念,只有符号不同的两个数互为相反数.解题时勿忘记正方体展开图的各种情形.
18.(1)长方体;(2)五棱柱
【分析】分别利用已知平面展开图进而分析得出答案.
【详解】解:如图(1)可以折成长方体,
如图(2)可以折成五棱柱.
【点睛】本题主要考查展开图折叠成几何体的知识点,熟记常见立体图形的平面展开图是解决此类问题的关键.
19.圆锥;圆柱;四棱锥
【解析】略
20.(1)它是六棱柱,它有12个顶点,18条棱;
(2)这个棱柱的所有侧面的面积之和是120
【分析】(1)根据棱柱面、顶点、棱之间的关系得出答案;
(2)计算侧面面积即可.
【详解】(1)解:因为一个直棱柱有8个面,所以它是六棱柱,
所以有12个顶点,18条棱,
答:它是六棱柱,它有12个顶点,18条棱;
(2)因为六棱柱的底面边长都是5cm,侧棱长都是4cm,
所以侧面展开后是长为5×6=30cm,宽为4cm的长方形,
因此侧面积为30×4=120(cm2),
答:这个棱柱的所有侧面的面积之和是120.
【点睛】此题考查了棱柱的面、顶点、棱之间的关系,计算侧面展开图的面积,正确掌握直棱柱的特点是解题的关键.
21.(1)8
(2)见解析
(3)这个长方体纸盒的体积为立方厘米,表面积为 平方厘米.
【分析】(1)根据长方体总共有12条棱,有4条棱未剪开,即可得出剪开的棱的条数;
(2)根据长方体的展开图的情况可知有4种情况;
(3)设底面边长为,根据棱长的和是,列出方程可求出底面边长,进而得到长方体纸盒的体积和表面积.
【详解】(1)解:由图可得,小明共剪了8条棱,
故答案为:8.
(2)如图,粘贴的位置有四种情况如下:
(3)∵长方体纸盒的底面是一个正方形,
∴可设底面边长,
∵长方体纸盒所有棱长的和是,长方体纸盒高为,
∴,
解得,
∴这个长方体纸盒的体积为:立方厘米.
这个长方体纸盒的表面积为:平方厘米.
【点睛】本题主要考查了几何展开图,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念,是解决此类问题的关键.
22.放在①⑦⑧⑨可围成正方体;放在②③④⑤⑥⑩不可以围成正方体.
【详解】【分析】先把已知的展开图折回,漏的空就是①⑦⑧⑨四边围成的正方形,所以只能放在这四个位置.
【详解】解:
放在①⑦⑧⑨可围成正方体;
放在②③④⑤⑥⑩不可以围成正方体.
【点睛】本题考核知识点:展开图与立体图形. 解题关键点:动手把展开图折回立体图形进行分析.
23.(1)(2)(3)
【分析】本题考查了平面展开图—最短路径问题,解答本题的关键是熟练运用数形结合的思想解决问题.
(1)直接利用勾股定理进行求解即可;
(2)将圆柱体展开,利用勾股定理求解即可;
(3)从玻璃杯侧面展开,作关于的对称点,根据两点之间线段最短可知的长度即为所求,利用勾股定理求解即可.
【详解】解:(1)由题意得,
故答案为:;
(2)将圆柱体展开,由题意得
,
故答案为:;
(3)如图,
从玻璃杯侧面展开,作关于的对称点,作交延长线于点,连接交于点,
,,
,
,
,
蚂蚁从外壁处到内壁处所爬行的最短路程是.
24.(1)作图见解析
(2)图①左不是正方体的展开图,图①右是正方体的展开图,图②是正方体的展开图.
【分析】(1)根据轴对称及中心对称图形的定义作图即可得到答案;
(2)由正方体的平面展开图验证即可判断.
【详解】(1)解:如图所示(所画轴对称图形不唯一):
图①是轴对称图形,图②是中心对称图形;
(2)解:由(1)中图形可知,图①左不是正方体的展开图,图①右是正方体的展开图,图②是正方体的展开图.
【点睛】本题考查中心对称图形与轴对称图形的定义、正方体的平面展开图等知识,熟练掌握中心对称图形与轴对称图形的定义是解决问题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
