2025年中考数学几何解题方法复习-- 第 13 节 圆的综合探究(含解析)
文档属性
| 名称 | 2025年中考数学几何解题方法复习-- 第 13 节 圆的综合探究(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 530.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 21:41:44 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第 13 节 圆的综合探究
一、知识梳理
定边对30°,45°,60°,120°定角类问题
①如图13-1所示,若∠P=30°,以AB 为边,同侧构造等边三角形AOB,点O即为△ABP的外接圆的圆心.
②如图13-2所示,若∠P=45°,以AB为斜边,同侧构造等腰直角三角形AOB,点O 即为△ABP 的外接圆的圆心.
③如图13-3所示,若∠P=60°,以AB为底,同侧构造顶角为 的等腰三角形AOB,点 O 即为△ABP的外接圆的圆心.
④如图13-4所示,若∠P=120°,以AB为底,异侧为边构造顶角为 的等腰三角形AOB,点O 即为△ABP的外接圆的圆心.
根据圆内接四边形对角互补可知,定边所对的与30°角同侧的轨迹是优弧,则其所对的与150°角同侧的轨迹是劣弧;定边所对的与45°角同侧的轨迹是优弧,则其所对的与135°角同侧的轨迹是劣弧;定边所对的与60°角同侧的轨迹是优弧,则其所对的与120°角同侧的轨迹是劣弧.
【例】如图13-5所示,在四边形ABCD中,∠ABC=60°,连接AC,BD 相交于点E,EC=2AE=4. 若BE=2ED,则BD的最大值为 .
解:如图 13-6所示,作△ABC 的外接圆⊙O,连接OB,OA,OC,OE,过点O作OH⊥AC于点H.
∵∠AOC=2∠ABC,∠ABC=60°,
∴∠AOC=120°.
∵EC=2AE=4,
∴AE=2.
∴AC=AE+EC=6.
∵OA=OC,OH⊥AC,
∴∠OAC=∠OCA=30°,AH=HC=3,EH=AH-AE=1.
∵BE≤OB+OE,
即BE的最大值为
∵BE=2DE,
∴ DE 的最大值为
∴ BD 的最大值为
二、分层练习
万丈高楼平地起
1.如图13-7所示,在半径为6cm的⊙O中,点A 是劣弧BC的中点,点D 是优弧BC上的一点,AO,BC相交于点 E,且∠D=30°,下列四个结论中正确的是 (填写序号).
①OA⊥BC;
④四边形ABOC 是菱形.
2. 如图13-8所示,AB 是⊙O 的直径,AM,BN是⊙O 的两条切线,点 C,D分别在AM,BN上,DC与⊙O相切于点 E,连接OD,OC,BE,AE,BE与OC 相交于点P,AE与OD 相交于点Q,AD=4,BC=9. 下列结论中正确的是 (填写序号).
①⊙O的半径为
②OD∥BE;
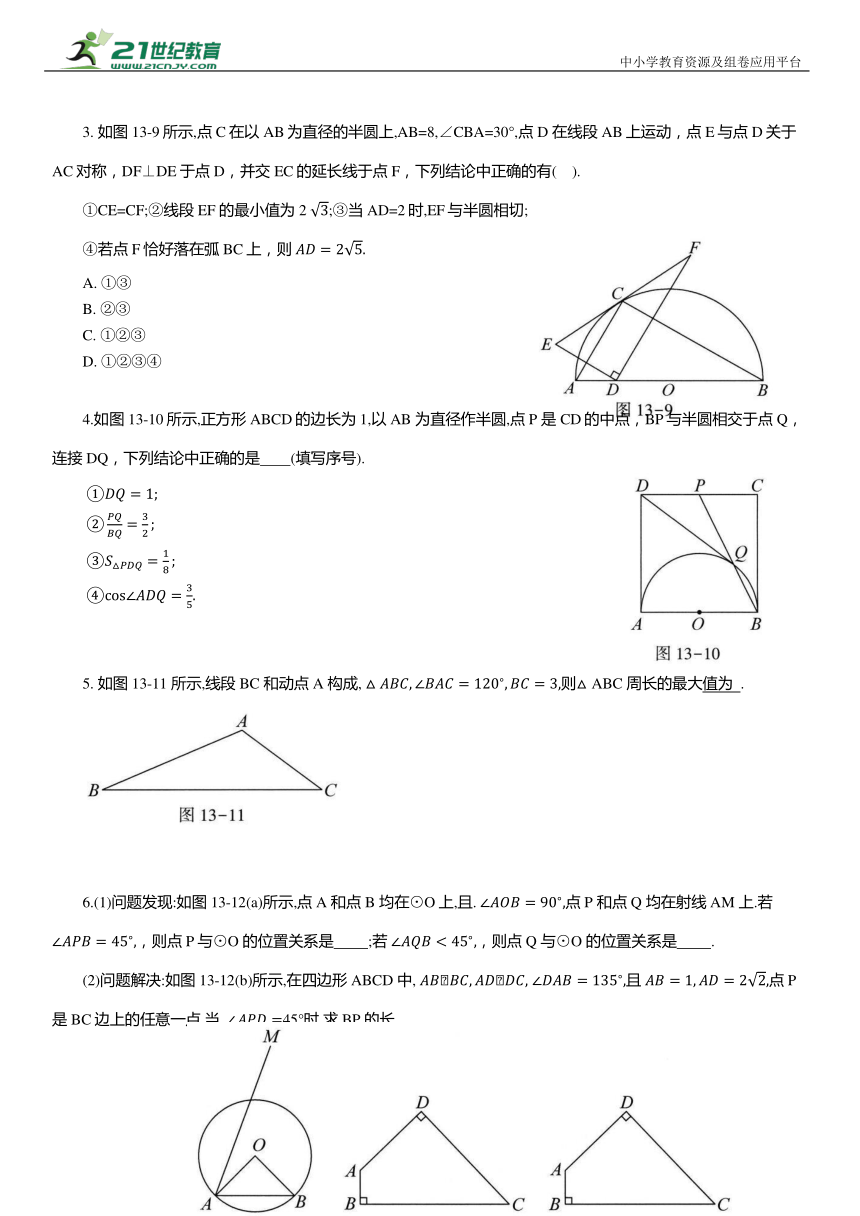
3. 如图13-9所示,点C在以AB为直径的半圆上,AB=8,∠CBA=30°,点D 在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点 D,并交EC的延长线于点 F,下列结论中正确的有( ).
①CE=CF;②线段EF 的最小值为2 ;③当AD=2时,EF与半圆相切;
④若点 F恰好落在弧 BC上,则
A. ①③
B. ②③
C. ①②③
D. ①②③④
4.如图13-10所示,正方形ABCD的边长为1,以AB 为直径作半圆,点 P 是CD的中点,BP与半圆相交于点 Q,连接DQ,下列结论中正确的是 (填写序号).
5. 如图13-11 所示,线段 BC 和动点 A 构成, 则△ABC 周长的最大值为 .
6.(1)问题发现:如图13-12(a)所示,点A 和点B 均在⊙O上,且. 点 P 和点 Q 均在射线AM 上.若 ,则点P与⊙O 的位置关系是 ;若 ,则点 Q 与⊙O 的位置关系是 .
(2)问题解决:如图13-12(b)所示,在四边形ABCD 中, 且 点 P 是 BC边上的任意一点.当. 45°时,求 BP 的长.
7. 如图13-13所示,在每一个四边形ABCD中,均有AD∥BC,CD⊥BC,∠ABC=60°,AD=8,BC=12.
(1)如图 13-13(a)所示,点 M 是 AD 上的任意一点,则. 的面积为 ;
(2)如图13-13(b)所示,点N是AD 上的任意一点,则 周长的最小值为 ;
(3)如图13-13(c)所示,在AD上是否存在一点 P,使得( 的值最小 若存在,求出此时cos∠BPC的值;若不存在,请说明理由.
8.一山庄的平面图为如图13-14所示的五边形ABCDE,山庄保卫人员想在线段CD上选一点 M 安装监控装置,监视边AB.现只要使 为 ,就可以让监控装置的效果达到最佳.已知∠ , ,问在线段 CD上是否存在点M,使 若存在,请求出符合条件的DM的长;若不存在,请说明理由.
第13节 圆的综合探究
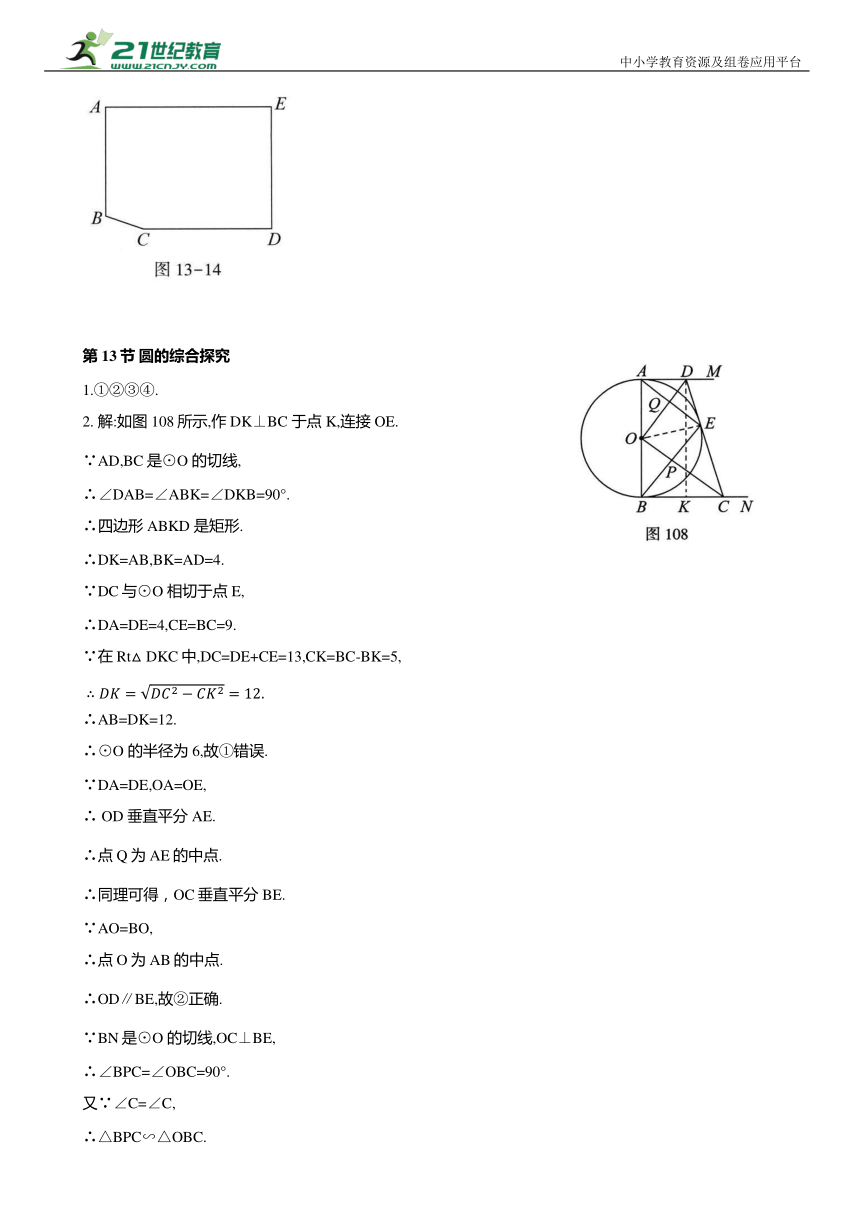
1.①②③④.
2. 解:如图108所示,作 DK⊥BC 于点 K,连接OE.
∵AD,BC是⊙O 的切线,
∴∠DAB=∠ABK=∠DKB=90°.
∴四边形ABKD 是矩形.
∴DK=AB,BK=AD=4.
∵DC与⊙O 相切于点 E,
∴DA=DE=4,CE=BC=9.
∵在Rt△DKC中,DC=DE+CE=13,CK=BC-BK=5,
∴AB=DK=12.
∴⊙O 的半径为6,故①错误.
∵DA=DE,OA=OE,
∴ OD 垂直平分AE.
∴点 Q为AE的中点.
∴同理可得,OC垂直平分BE.
∵AO=BO,
∴点O为AB的中点.
∴OD∥BE,故②正确.
∵BN是⊙O 的切线,OC⊥BE,
∴∠BPC=∠OBC=90°.
又∵∠C=∠C,
∴△BPC∽△OBC.
∵在△OBC中,
故③正确.
∵CE=CB,
∴ ∠CEB=∠CBE.
故④错误.
故答案为②③正确.
3. 解:如图109所示,连接DC,CO.
∵点E与点D关于AC对称,
∴∠E=∠CDE.
∴∠EDF=90°.
∴ ∠E+∠F=90°.
∵∠CDE+∠CDF=90°,
∴∠F=∠CDF.
∴CD=CF.
∴CE=CD=CF,故①正确.
∵CE=CD=CF,
∴EF=2CD.
∴当CD最小时,EF最小.
∴当CD⊥AB时,CD最小.
∵AB是半⊙O的直径,
∴∠ACB=90°.
∵AB=8,∠CBA=30°,
∵在 Rt△ADC中,
∴线段EF的最小值为 故②不正确.
∵OA=OC,∠A=60°,
∴△AOC 是等边三角形.
∴AD=OD.
∵点E与点 D 关于AC 对称,
∴∠ECA=∠ACD=30°.
∴∠OCE=∠ECA+∠ACO=90°.
∵OC是半⊙O的半径,
∴ EF 与半⊙O 相切,故③正确.
如图110所示,当点 F 恰好落在弧 BC上时,连接AF,BF,且AC,ED 相交于点 G.
∵点E与点 D 关于AC对称,
∴FH=DH.
∵∠EDF=90°,BC∥DE,
∴∠BHD=∠EDF=90°.
∴ BC是DF的垂直平分线.
∴BF=BD.
∴∠FBA=2∠CBA=60°.
∵AB 是半⊙O的直径,
∴∠AFB=90°.
∴BD=BF=4.
∴AD=AB-BD=8-4=4,故④不正确.
故选A.
4. 连接OQ,OD,如图111 所示.
∵四边形ABCD为正方形,
∴DC∥AB.
∵点P是CD的中点,AB为半圆的直径,点O 为半圆的圆心,
∴DP=OB.
∴四边形DPBO 为平行四边形.
∴DO∥BP.
∴∠AOD=∠OBQ,∠QOD=∠OQB.
∵OQ=OB,
∴ ∠AOD=∠QOD.
又∵AO=QO,DO=DO,
∴ △AOD≌△QOD(SAS).
∴DQ=DA=1,故①正确.
连接AQ,如图112所示.
∵正方形ABCD 的边长为1,点 P 是 CD的中点,
∵∠ABQ+∠QAB=90°,∠PBC+∠ABP=90°,
∴∠PBC=∠QAB.
∴Rt△AQB∽Rt△BCP.
艮 解得
故②正确.
③过点 Q 作 QH⊥DC 于点H,如图113所示.
∵ QH⊥DC,∠C=90°,
∴△PHQ∽△PCB.
I 解得
故③错误.
④过点 Q 作 QN⊥AD 于点 N,如图114 所示.
∵四边形ABCD为正方形,QN⊥AD,
∴DP∥NQ∥AB.
∵AD=1,
解得
∵DQ=1,
故④正确.
综上所述,正确的结论是①②④.
☆欲穷千里目,更上一层楼
5. 解:如图115所示,延长BA 到点 D,使AD=AC,连接CD,作△BCD的外接圆⊙O,设⊙O的半径为r,连接OB,OC,过点O作OE⊥BC于点 E.
∵AD=AC,
∴ △ABC的周长=AB+BC+AC=AB+BC+AD=BD+BC.
∵BC=3,
∴当 BD的长度最大时,△ABC周长最大.
∴当点A 与点O 重合,BD为⊙O 的直径时,BD最大.
∵∠BAC=120°,
∵BC=3,OE⊥BC,
艮 解得
∴ BD 的最大值为
∴△ABC周长的最大值为
6. 解:
∴点P在⊙O上.
∵∠AQB<45°,
∴点Q 在⊙O外.
(2)如图116所示,构造等腰直角三角形△AOD,以点O 为圆心,OA为半径作⊙O 交BC于点 P,P',延长DO交BC于点H,连接DP,DP',OP',OP,AP,AP'.
∵∠DAB=135°,∠DAO=45°,
∴∠OAB=∠B=90°.
∴OA∥BC.
∴∠OHB=∠DOA=90°.
∴四边形 ABHO 是矩形.
∴OH=AB=1,OA=BH.
∴OA=OD=OP=OP'=2.
∴在 Rt△OPH和 Rt△OP'H中,
∵BH=OA=2,
7. 解:(1)如图117所示,过点A作AE⊥BC于点 E.
∵AD∥BC,CD⊥BC,AE⊥BC,
∴四边形AECD是矩形.
∴EC=AD=8,BE=BC-EC=12-8=4.
∵在Rt△ABE中,∠ABE=60°,BE=4,
(2)如图118所示,过点A作AE⊥BC,作点C关于直线AD的对称点( 连接C'B交AD 于点 N',连接CN',C'N,C'D,则,
△BNC周长的最小值=△BN'C 的周长:
∵AD∥BC,AE⊥BC,∠ABC=60°,
∴CE=AD=8.
∵BC=12,
∴△BNC 周长的最小值为
(3)如图119所示,存在点 P,使得( 的值最小,作BC的中垂线 PQ 交 BC 于点 Q,交 AD 于点 P,连接BP,CP,作 的外接圆⊙O,⊙O 与直线 PQ 相交于点N,则 圆心O在PN上,在AD上任取一点. 连接P'B,P'C,P'B交⊙O于点 M,连接MC.
∵AD∥BC,⊙O是△BPC的外接圆,
∴⊙O 与AD 相切于点 P.
∴∠QPD=90°.
∴∠ADC=∠BCD=90°.
∴ 四边形 PQCD 是矩形.
∴ PQ>BQ.
∴ ∠BPC<90°,圆心O在弦BC 的上方.
∴∠BPC=∠BMC≥∠BP'C.
∴∠BPC 最大,cos∠BPC 的值最小.
连接OB,则∠BON=2∠BPN=∠BPC.
在 Rt△BOQ 中,根据勾股定理得 解得
会当凌绝顶,一览众山小
8. 解:在线段CD上存在点 M,使∠AMB=60°.
以AB为边,在AB的右侧作等边三角形ABG,作( 于点 P,作AK⊥BG于点K,设GP与AK相交于点O,以点O为圆心,OA为半径作⊙O,过点O 作OH⊥CD于点H,则⊙O 是△ABG的外接圆,如图120所示.
∵△ABG是等边三角形,GP⊥AB,AB=270m,
∵ED=285m,
∴OH=285-135=150(m).
∵△ABG是等边三角形,AK⊥BG,
∴∠BAK=∠GAK=30°.
∴OH∴⊙O与CD相交,设交点为点M,连接MA,MB,见图120.
∵OH⊥CD,OH=150m,
若点M在点H的左侧,
则.
即DM>CD,
∴点M 不在线段CD上,应舍去.
若点M在点H的右侧,则
即
∴点 M 在线段CD上.
综上所述,在线段CD 上存在唯一的点 M,使 ,此时 DM 的长为
第 13 节 圆的综合探究
一、知识梳理
定边对30°,45°,60°,120°定角类问题
①如图13-1所示,若∠P=30°,以AB 为边,同侧构造等边三角形AOB,点O即为△ABP的外接圆的圆心.
②如图13-2所示,若∠P=45°,以AB为斜边,同侧构造等腰直角三角形AOB,点O 即为△ABP 的外接圆的圆心.
③如图13-3所示,若∠P=60°,以AB为底,同侧构造顶角为 的等腰三角形AOB,点 O 即为△ABP的外接圆的圆心.
④如图13-4所示,若∠P=120°,以AB为底,异侧为边构造顶角为 的等腰三角形AOB,点O 即为△ABP的外接圆的圆心.
根据圆内接四边形对角互补可知,定边所对的与30°角同侧的轨迹是优弧,则其所对的与150°角同侧的轨迹是劣弧;定边所对的与45°角同侧的轨迹是优弧,则其所对的与135°角同侧的轨迹是劣弧;定边所对的与60°角同侧的轨迹是优弧,则其所对的与120°角同侧的轨迹是劣弧.
【例】如图13-5所示,在四边形ABCD中,∠ABC=60°,连接AC,BD 相交于点E,EC=2AE=4. 若BE=2ED,则BD的最大值为 .
解:如图 13-6所示,作△ABC 的外接圆⊙O,连接OB,OA,OC,OE,过点O作OH⊥AC于点H.
∵∠AOC=2∠ABC,∠ABC=60°,
∴∠AOC=120°.
∵EC=2AE=4,
∴AE=2.
∴AC=AE+EC=6.
∵OA=OC,OH⊥AC,
∴∠OAC=∠OCA=30°,AH=HC=3,EH=AH-AE=1.
∵BE≤OB+OE,
即BE的最大值为
∵BE=2DE,
∴ DE 的最大值为
∴ BD 的最大值为
二、分层练习
万丈高楼平地起
1.如图13-7所示,在半径为6cm的⊙O中,点A 是劣弧BC的中点,点D 是优弧BC上的一点,AO,BC相交于点 E,且∠D=30°,下列四个结论中正确的是 (填写序号).
①OA⊥BC;
④四边形ABOC 是菱形.
2. 如图13-8所示,AB 是⊙O 的直径,AM,BN是⊙O 的两条切线,点 C,D分别在AM,BN上,DC与⊙O相切于点 E,连接OD,OC,BE,AE,BE与OC 相交于点P,AE与OD 相交于点Q,AD=4,BC=9. 下列结论中正确的是 (填写序号).
①⊙O的半径为
②OD∥BE;
3. 如图13-9所示,点C在以AB为直径的半圆上,AB=8,∠CBA=30°,点D 在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点 D,并交EC的延长线于点 F,下列结论中正确的有( ).
①CE=CF;②线段EF 的最小值为2 ;③当AD=2时,EF与半圆相切;
④若点 F恰好落在弧 BC上,则
A. ①③
B. ②③
C. ①②③
D. ①②③④
4.如图13-10所示,正方形ABCD的边长为1,以AB 为直径作半圆,点 P 是CD的中点,BP与半圆相交于点 Q,连接DQ,下列结论中正确的是 (填写序号).
5. 如图13-11 所示,线段 BC 和动点 A 构成, 则△ABC 周长的最大值为 .
6.(1)问题发现:如图13-12(a)所示,点A 和点B 均在⊙O上,且. 点 P 和点 Q 均在射线AM 上.若 ,则点P与⊙O 的位置关系是 ;若 ,则点 Q 与⊙O 的位置关系是 .
(2)问题解决:如图13-12(b)所示,在四边形ABCD 中, 且 点 P 是 BC边上的任意一点.当. 45°时,求 BP 的长.
7. 如图13-13所示,在每一个四边形ABCD中,均有AD∥BC,CD⊥BC,∠ABC=60°,AD=8,BC=12.
(1)如图 13-13(a)所示,点 M 是 AD 上的任意一点,则. 的面积为 ;
(2)如图13-13(b)所示,点N是AD 上的任意一点,则 周长的最小值为 ;
(3)如图13-13(c)所示,在AD上是否存在一点 P,使得( 的值最小 若存在,求出此时cos∠BPC的值;若不存在,请说明理由.
8.一山庄的平面图为如图13-14所示的五边形ABCDE,山庄保卫人员想在线段CD上选一点 M 安装监控装置,监视边AB.现只要使 为 ,就可以让监控装置的效果达到最佳.已知∠ , ,问在线段 CD上是否存在点M,使 若存在,请求出符合条件的DM的长;若不存在,请说明理由.
第13节 圆的综合探究
1.①②③④.
2. 解:如图108所示,作 DK⊥BC 于点 K,连接OE.
∵AD,BC是⊙O 的切线,
∴∠DAB=∠ABK=∠DKB=90°.
∴四边形ABKD 是矩形.
∴DK=AB,BK=AD=4.
∵DC与⊙O 相切于点 E,
∴DA=DE=4,CE=BC=9.
∵在Rt△DKC中,DC=DE+CE=13,CK=BC-BK=5,
∴AB=DK=12.
∴⊙O 的半径为6,故①错误.
∵DA=DE,OA=OE,
∴ OD 垂直平分AE.
∴点 Q为AE的中点.
∴同理可得,OC垂直平分BE.
∵AO=BO,
∴点O为AB的中点.
∴OD∥BE,故②正确.
∵BN是⊙O 的切线,OC⊥BE,
∴∠BPC=∠OBC=90°.
又∵∠C=∠C,
∴△BPC∽△OBC.
∵在△OBC中,
故③正确.
∵CE=CB,
∴ ∠CEB=∠CBE.
故④错误.
故答案为②③正确.
3. 解:如图109所示,连接DC,CO.
∵点E与点D关于AC对称,
∴∠E=∠CDE.
∴∠EDF=90°.
∴ ∠E+∠F=90°.
∵∠CDE+∠CDF=90°,
∴∠F=∠CDF.
∴CD=CF.
∴CE=CD=CF,故①正确.
∵CE=CD=CF,
∴EF=2CD.
∴当CD最小时,EF最小.
∴当CD⊥AB时,CD最小.
∵AB是半⊙O的直径,
∴∠ACB=90°.
∵AB=8,∠CBA=30°,
∵在 Rt△ADC中,
∴线段EF的最小值为 故②不正确.
∵OA=OC,∠A=60°,
∴△AOC 是等边三角形.
∴AD=OD.
∵点E与点 D 关于AC 对称,
∴∠ECA=∠ACD=30°.
∴∠OCE=∠ECA+∠ACO=90°.
∵OC是半⊙O的半径,
∴ EF 与半⊙O 相切,故③正确.
如图110所示,当点 F 恰好落在弧 BC上时,连接AF,BF,且AC,ED 相交于点 G.
∵点E与点 D 关于AC对称,
∴FH=DH.
∵∠EDF=90°,BC∥DE,
∴∠BHD=∠EDF=90°.
∴ BC是DF的垂直平分线.
∴BF=BD.
∴∠FBA=2∠CBA=60°.
∵AB 是半⊙O的直径,
∴∠AFB=90°.
∴BD=BF=4.
∴AD=AB-BD=8-4=4,故④不正确.
故选A.
4. 连接OQ,OD,如图111 所示.
∵四边形ABCD为正方形,
∴DC∥AB.
∵点P是CD的中点,AB为半圆的直径,点O 为半圆的圆心,
∴DP=OB.
∴四边形DPBO 为平行四边形.
∴DO∥BP.
∴∠AOD=∠OBQ,∠QOD=∠OQB.
∵OQ=OB,
∴ ∠AOD=∠QOD.
又∵AO=QO,DO=DO,
∴ △AOD≌△QOD(SAS).
∴DQ=DA=1,故①正确.
连接AQ,如图112所示.
∵正方形ABCD 的边长为1,点 P 是 CD的中点,
∵∠ABQ+∠QAB=90°,∠PBC+∠ABP=90°,
∴∠PBC=∠QAB.
∴Rt△AQB∽Rt△BCP.
艮 解得
故②正确.
③过点 Q 作 QH⊥DC 于点H,如图113所示.
∵ QH⊥DC,∠C=90°,
∴△PHQ∽△PCB.
I 解得
故③错误.
④过点 Q 作 QN⊥AD 于点 N,如图114 所示.
∵四边形ABCD为正方形,QN⊥AD,
∴DP∥NQ∥AB.
∵AD=1,
解得
∵DQ=1,
故④正确.
综上所述,正确的结论是①②④.
☆欲穷千里目,更上一层楼
5. 解:如图115所示,延长BA 到点 D,使AD=AC,连接CD,作△BCD的外接圆⊙O,设⊙O的半径为r,连接OB,OC,过点O作OE⊥BC于点 E.
∵AD=AC,
∴ △ABC的周长=AB+BC+AC=AB+BC+AD=BD+BC.
∵BC=3,
∴当 BD的长度最大时,△ABC周长最大.
∴当点A 与点O 重合,BD为⊙O 的直径时,BD最大.
∵∠BAC=120°,
∵BC=3,OE⊥BC,
艮 解得
∴ BD 的最大值为
∴△ABC周长的最大值为
6. 解:
∴点P在⊙O上.
∵∠AQB<45°,
∴点Q 在⊙O外.
(2)如图116所示,构造等腰直角三角形△AOD,以点O 为圆心,OA为半径作⊙O 交BC于点 P,P',延长DO交BC于点H,连接DP,DP',OP',OP,AP,AP'.
∵∠DAB=135°,∠DAO=45°,
∴∠OAB=∠B=90°.
∴OA∥BC.
∴∠OHB=∠DOA=90°.
∴四边形 ABHO 是矩形.
∴OH=AB=1,OA=BH.
∴OA=OD=OP=OP'=2.
∴在 Rt△OPH和 Rt△OP'H中,
∵BH=OA=2,
7. 解:(1)如图117所示,过点A作AE⊥BC于点 E.
∵AD∥BC,CD⊥BC,AE⊥BC,
∴四边形AECD是矩形.
∴EC=AD=8,BE=BC-EC=12-8=4.
∵在Rt△ABE中,∠ABE=60°,BE=4,
(2)如图118所示,过点A作AE⊥BC,作点C关于直线AD的对称点( 连接C'B交AD 于点 N',连接CN',C'N,C'D,则,
△BNC周长的最小值=△BN'C 的周长:
∵AD∥BC,AE⊥BC,∠ABC=60°,
∴CE=AD=8.
∵BC=12,
∴△BNC 周长的最小值为
(3)如图119所示,存在点 P,使得( 的值最小,作BC的中垂线 PQ 交 BC 于点 Q,交 AD 于点 P,连接BP,CP,作 的外接圆⊙O,⊙O 与直线 PQ 相交于点N,则 圆心O在PN上,在AD上任取一点. 连接P'B,P'C,P'B交⊙O于点 M,连接MC.
∵AD∥BC,⊙O是△BPC的外接圆,
∴⊙O 与AD 相切于点 P.
∴∠QPD=90°.
∴∠ADC=∠BCD=90°.
∴ 四边形 PQCD 是矩形.
∴ PQ>BQ.
∴ ∠BPC<90°,圆心O在弦BC 的上方.
∴∠BPC=∠BMC≥∠BP'C.
∴∠BPC 最大,cos∠BPC 的值最小.
连接OB,则∠BON=2∠BPN=∠BPC.
在 Rt△BOQ 中,根据勾股定理得 解得
会当凌绝顶,一览众山小
8. 解:在线段CD上存在点 M,使∠AMB=60°.
以AB为边,在AB的右侧作等边三角形ABG,作( 于点 P,作AK⊥BG于点K,设GP与AK相交于点O,以点O为圆心,OA为半径作⊙O,过点O 作OH⊥CD于点H,则⊙O 是△ABG的外接圆,如图120所示.
∵△ABG是等边三角形,GP⊥AB,AB=270m,
∵ED=285m,
∴OH=285-135=150(m).
∵△ABG是等边三角形,AK⊥BG,
∴∠BAK=∠GAK=30°.
∴OH
∵OH⊥CD,OH=150m,
若点M在点H的左侧,
则.
即DM>CD,
∴点M 不在线段CD上,应舍去.
若点M在点H的右侧,则
即
∴点 M 在线段CD上.
综上所述,在线段CD 上存在唯一的点 M,使 ,此时 DM 的长为
同课章节目录
