2025年中考数学几何解题方法复习--第1节 圆的认识(含解析)
文档属性
| 名称 | 2025年中考数学几何解题方法复习--第1节 圆的认识(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 312.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 21:49:01 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第1节 圆的认识
一、知识梳理
1.圆的基本概念
弦:连接圆上任意两点的线段叫作弦.
直径:经过圆心的弦叫作直径.
圆弧:圆上任意两点间的部分叫作圆弧.弧包括优弧和劣弧,大于半圆的弧叫作优弧,小于半圆的弧叫作劣弧.
半圆:圆的任意一条直径的两个端点将圆分成两条弧,每一条弧都叫作半圆.
等圆:能够重合的两个圆叫作等圆.
等弧:在同圆或等圆中,能够互相重合的弧叫作等弧.
2.圆的对称性
圆是轴对称图形,其对称轴是任意一条过圆心的直线.
圆是中心对称图形,对称中心为圆心.
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.
在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
3.点与圆的位置关系
设⊙O的半径为r,点P 到圆心O 的距离为d,则有:
①点在圆外 d>r;
②点在圆上 d=r;
③点在圆内 d【例】如图1-1 所示,AB是⊙O 的直径,四边形ABCD 内接于⊙O. 若BC=CD=DA=4cm,则⊙O的周长为( ).
A. 5πcm B. 6πcm C. 9πcm D. 8πcm
解:如图1-2所示,连接OD,OC.
∵AB 是⊙O的直径,四边形ABCD 内接于⊙O,
∴∠AOD=∠DOC=∠COB=60°.
又∵OA=OD,
∴△AOD是等边三角形.
∴OA=AD=4cm.
∴⊙O 的周长=2π×4=8π(cm).
故选 D.
二、分层练习
1.下列命题正确的个数是( )个.
①直径是圆中最大的弦;
②长度相等的两条弧一定是等弧;
③半径相等的两个圆是等圆;
④面积相等的两个圆是等圆;
⑤ 同一条弦所对的两条弧一定是等弧;
A. 2 B. 3 C. 4 D. 5
2.小明不慎把家里的圆形玻璃打碎了,其中四块碎片如图1-3所示.为了在商店配到与原来大小一样的圆形玻璃,小明要选择携带的应该是( ).
A. 第①块
B. 第②块
C. 第③块
D. 第④块
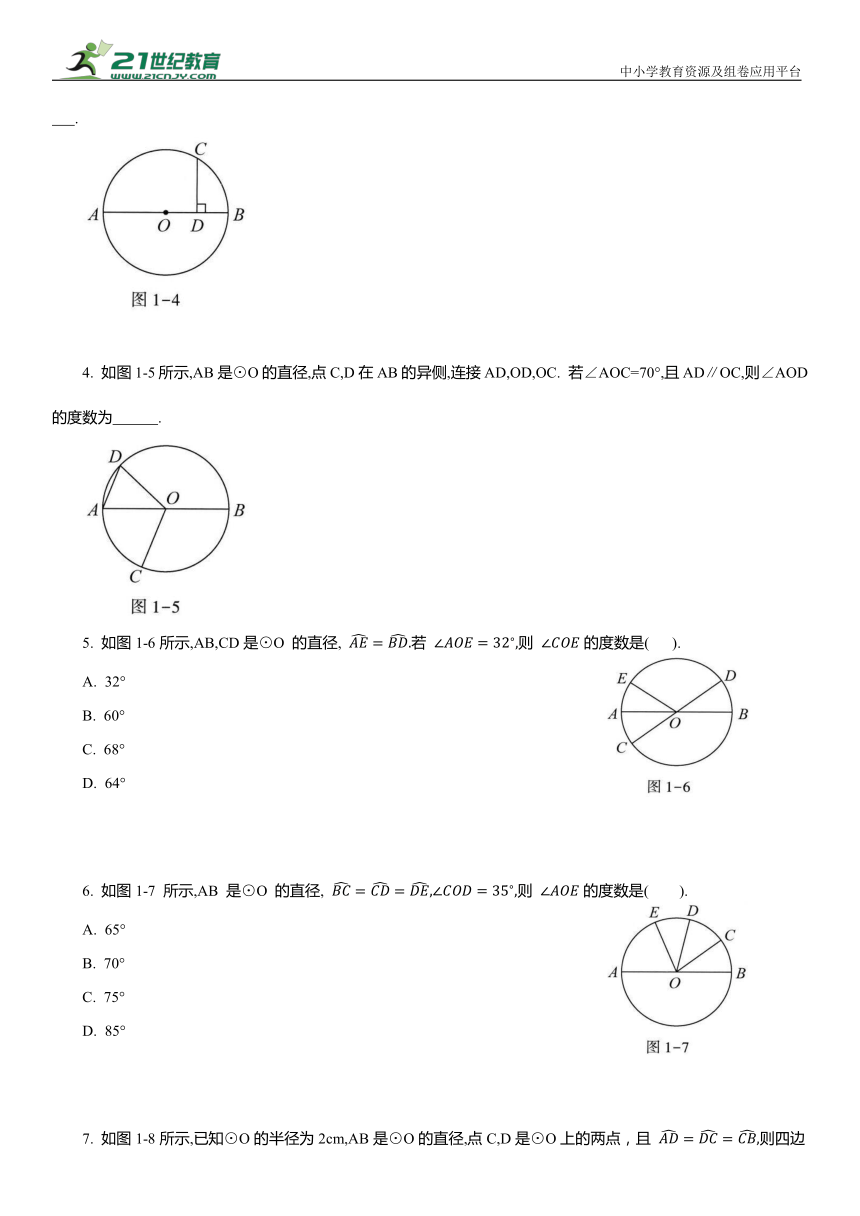
3. 如图1-4所示,AB是⊙O 的直径,点C在⊙O上,( 垂足为点 D.已知CD=4,OD=3,则AB的长为 .
4. 如图1-5所示,AB是⊙O的直径,点C,D在AB的异侧,连接AD,OD,OC. 若∠AOC=70°,且AD∥OC,则∠AOD的度数为 .
5. 如图1-6所示,AB,CD是⊙O 的直径, 若 则 的度数是( ).
A. 32°
B. 60°
C. 68°
D. 64°
6. 如图1-7 所示,AB 是⊙O 的直径, 则 的度数是( ).
A. 65°
B. 70°
C. 75°
D. 85°
7. 如图1-8所示,已知⊙O的半径为2cm,AB是⊙O的直径,点C,D是⊙O上的两点,且 则四边形ABCD 的周长为().
A. 8cm
B. 10cm
C. 12cm
D. 16cm
8. 如图1-9所示,在⊙O中,如果 那么( ).
A. AB=AC
B. AB=2AC
C. AB<2AC
D. AB>2AC
9. 如图1-10 所示,在矩形ABCD 中, 点 P 在边AB上,且. 3AP.如果圆 P 是以点 P 为圆心,PD 为半径的圆,那么下列判断正确的是( ).
A. 点 B,C均在圆 P外
B.点 B 在圆 P外,点 C在圆 P内
C.点B在圆 P内,点 C 在圆 P外
D. 点 B,C均在圆P内
10.如图1-11所示,城市A的正北方向50km的B处,有一无线电信号发射塔,该发射塔发射的无线电信号的有效半径为100km,AC是一条直达C城的公路,从 A 城开往C城的班车速度为60km/h.
(1)当班车从A 城出发开往C城时,有人立即打开无线电收音机,班车行驶了0.5h时接收信号最强,则此时班车到发射塔的距离是多少 (离发射塔越近,信号越强)
(2)班车从A城到C城共行驶2h,请你判断,班车到C城后还能接收到信号吗 请说明理由.
11.如图1-12 所示,已知点A 是半圆上的三等分点,点B 是 的中点,点P 是直径MN上一动点,⊙O 的半径为1.请问:点P 在 MN 上什么位置时, 的值最小 并给出AP+BP 的最小值.
第1节 圆的认识
1.解:①直径是圆中最大的弦,正确;
②长度相等的两条弧一定是等弧,错误;
③半径相等的两个圆是等圆,正确;
④面积相等的两个圆是等圆,正确;
⑤ 同一条弦所对的两条弧一定是等弧,错误.
故选 B.
2.解:第①块出现一段完整的弧,可在这段弧上任意作两条弦,再作出这两条弦的垂直平分线,其交点为圆心,进而可得到半径的长.
故选 A.
3. 解:连接OC,如图1所示.
∵CD=4,OD=3,CD⊥AB,
∴AB=2OC=10.
4. 解:∵AD∥OC,
∴∠DAO=∠AOC=70°.
又∵OD=OA,
∴∠ADO=∠DAO=70°.
☆欲穷千里目,更上一层楼
5. 解:
∴∠BOD=∠AOE=32°.
∵∠BOD=∠AOC,
∴∠AOC=32°.
故选 D.
6. 解:
∴∠BOC=∠DOE=∠COD=35°.
∴ ∠AOE=180°-∠DOE-∠COD-∠BOC=75°.
故选 C.
7. 解:如图2所示,连接OD,OC.
∴∠AOD=∠DOC=∠COB.
∵AB 是⊙O的直径,
∴∠AOD+∠DOC+∠COB=180°.
∴∠AOD=∠DOC=∠COB=60°.
∵OA=OD,
∴△AOD 是等边三角形.
∴AD=DO=OA.
∵同理可得,OC=OD=CD,OC=OB=BC,
∴AD=CD=BC=OA=2cm.
∴四边形ABCD的周长=AD+CD+BC+AB=5OA=5×2=10(cm).故选 B.
8. 解:如图3所示,取弧AB的中点D,连接AD,DB.
∴AD=BD=AC.
∵在△ADB中,由三角形的三边关系可知
∴2AC>AB,即AB<2AC.
故选 C.
9. 解:∵四边形ABCD 为矩形,
∵AB=8,BP=3AP,
∴AP=2,BP=6.
∵在 Rt△ADP中,AP=2,AD=3
∵在Rt△PBC中,PB=6,BC=3
∴PC>PD>PB,即点 B在圆 P内,点 C在圆 P外.
故选C.
10. 解:(1)如图4所示,过点 B 作 BM⊥AC于点 M.
点M 是公路AC上距离点 B 最近的位置,班车行驶了
0.5h时接受信号最强,则班车行驶0.5h时到达点 M.
∵BM⊥AC,AM=30km,AB=50km.
∴ BM=40km.
答:班车到发射塔的距离是40km.
(2)如图5所示,连接BC.
∵AC=60×2=120km,AM=30km,
∴CM=AC-AM=90km.
答:班车到 C 城能接收到信号.
会当凌绝顶,一览众山小
11.解:如图6所示,作点A 关于MN的对称点A',根据圆的对称性,点A'必在圆上;连接BA'交MN于点 P,连接PA,则PA+PB最小,此时 A'B;连接OA,OA',OB.
∴∠AON=∠A'ON=60°.
∵点B是 的中点,
∴∠A'OB=90°.
∵⊙O 的半径为1,
即AP+BP的最小值为
第1节 圆的认识
一、知识梳理
1.圆的基本概念
弦:连接圆上任意两点的线段叫作弦.
直径:经过圆心的弦叫作直径.
圆弧:圆上任意两点间的部分叫作圆弧.弧包括优弧和劣弧,大于半圆的弧叫作优弧,小于半圆的弧叫作劣弧.
半圆:圆的任意一条直径的两个端点将圆分成两条弧,每一条弧都叫作半圆.
等圆:能够重合的两个圆叫作等圆.
等弧:在同圆或等圆中,能够互相重合的弧叫作等弧.
2.圆的对称性
圆是轴对称图形,其对称轴是任意一条过圆心的直线.
圆是中心对称图形,对称中心为圆心.
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.
在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
3.点与圆的位置关系
设⊙O的半径为r,点P 到圆心O 的距离为d,则有:
①点在圆外 d>r;
②点在圆上 d=r;
③点在圆内 d
A. 5πcm B. 6πcm C. 9πcm D. 8πcm
解:如图1-2所示,连接OD,OC.
∵AB 是⊙O的直径,四边形ABCD 内接于⊙O,
∴∠AOD=∠DOC=∠COB=60°.
又∵OA=OD,
∴△AOD是等边三角形.
∴OA=AD=4cm.
∴⊙O 的周长=2π×4=8π(cm).
故选 D.
二、分层练习
1.下列命题正确的个数是( )个.
①直径是圆中最大的弦;
②长度相等的两条弧一定是等弧;
③半径相等的两个圆是等圆;
④面积相等的两个圆是等圆;
⑤ 同一条弦所对的两条弧一定是等弧;
A. 2 B. 3 C. 4 D. 5
2.小明不慎把家里的圆形玻璃打碎了,其中四块碎片如图1-3所示.为了在商店配到与原来大小一样的圆形玻璃,小明要选择携带的应该是( ).
A. 第①块
B. 第②块
C. 第③块
D. 第④块
3. 如图1-4所示,AB是⊙O 的直径,点C在⊙O上,( 垂足为点 D.已知CD=4,OD=3,则AB的长为 .
4. 如图1-5所示,AB是⊙O的直径,点C,D在AB的异侧,连接AD,OD,OC. 若∠AOC=70°,且AD∥OC,则∠AOD的度数为 .
5. 如图1-6所示,AB,CD是⊙O 的直径, 若 则 的度数是( ).
A. 32°
B. 60°
C. 68°
D. 64°
6. 如图1-7 所示,AB 是⊙O 的直径, 则 的度数是( ).
A. 65°
B. 70°
C. 75°
D. 85°
7. 如图1-8所示,已知⊙O的半径为2cm,AB是⊙O的直径,点C,D是⊙O上的两点,且 则四边形ABCD 的周长为().
A. 8cm
B. 10cm
C. 12cm
D. 16cm
8. 如图1-9所示,在⊙O中,如果 那么( ).
A. AB=AC
B. AB=2AC
C. AB<2AC
D. AB>2AC
9. 如图1-10 所示,在矩形ABCD 中, 点 P 在边AB上,且. 3AP.如果圆 P 是以点 P 为圆心,PD 为半径的圆,那么下列判断正确的是( ).
A. 点 B,C均在圆 P外
B.点 B 在圆 P外,点 C在圆 P内
C.点B在圆 P内,点 C 在圆 P外
D. 点 B,C均在圆P内
10.如图1-11所示,城市A的正北方向50km的B处,有一无线电信号发射塔,该发射塔发射的无线电信号的有效半径为100km,AC是一条直达C城的公路,从 A 城开往C城的班车速度为60km/h.
(1)当班车从A 城出发开往C城时,有人立即打开无线电收音机,班车行驶了0.5h时接收信号最强,则此时班车到发射塔的距离是多少 (离发射塔越近,信号越强)
(2)班车从A城到C城共行驶2h,请你判断,班车到C城后还能接收到信号吗 请说明理由.
11.如图1-12 所示,已知点A 是半圆上的三等分点,点B 是 的中点,点P 是直径MN上一动点,⊙O 的半径为1.请问:点P 在 MN 上什么位置时, 的值最小 并给出AP+BP 的最小值.
第1节 圆的认识
1.解:①直径是圆中最大的弦,正确;
②长度相等的两条弧一定是等弧,错误;
③半径相等的两个圆是等圆,正确;
④面积相等的两个圆是等圆,正确;
⑤ 同一条弦所对的两条弧一定是等弧,错误.
故选 B.
2.解:第①块出现一段完整的弧,可在这段弧上任意作两条弦,再作出这两条弦的垂直平分线,其交点为圆心,进而可得到半径的长.
故选 A.
3. 解:连接OC,如图1所示.
∵CD=4,OD=3,CD⊥AB,
∴AB=2OC=10.
4. 解:∵AD∥OC,
∴∠DAO=∠AOC=70°.
又∵OD=OA,
∴∠ADO=∠DAO=70°.
☆欲穷千里目,更上一层楼
5. 解:
∴∠BOD=∠AOE=32°.
∵∠BOD=∠AOC,
∴∠AOC=32°.
故选 D.
6. 解:
∴∠BOC=∠DOE=∠COD=35°.
∴ ∠AOE=180°-∠DOE-∠COD-∠BOC=75°.
故选 C.
7. 解:如图2所示,连接OD,OC.
∴∠AOD=∠DOC=∠COB.
∵AB 是⊙O的直径,
∴∠AOD+∠DOC+∠COB=180°.
∴∠AOD=∠DOC=∠COB=60°.
∵OA=OD,
∴△AOD 是等边三角形.
∴AD=DO=OA.
∵同理可得,OC=OD=CD,OC=OB=BC,
∴AD=CD=BC=OA=2cm.
∴四边形ABCD的周长=AD+CD+BC+AB=5OA=5×2=10(cm).故选 B.
8. 解:如图3所示,取弧AB的中点D,连接AD,DB.
∴AD=BD=AC.
∵在△ADB中,由三角形的三边关系可知
∴2AC>AB,即AB<2AC.
故选 C.
9. 解:∵四边形ABCD 为矩形,
∵AB=8,BP=3AP,
∴AP=2,BP=6.
∵在 Rt△ADP中,AP=2,AD=3
∵在Rt△PBC中,PB=6,BC=3
∴PC>PD>PB,即点 B在圆 P内,点 C在圆 P外.
故选C.
10. 解:(1)如图4所示,过点 B 作 BM⊥AC于点 M.
点M 是公路AC上距离点 B 最近的位置,班车行驶了
0.5h时接受信号最强,则班车行驶0.5h时到达点 M.
∵BM⊥AC,AM=30km,AB=50km.
∴ BM=40km.
答:班车到发射塔的距离是40km.
(2)如图5所示,连接BC.
∵AC=60×2=120km,AM=30km,
∴CM=AC-AM=90km.
答:班车到 C 城能接收到信号.
会当凌绝顶,一览众山小
11.解:如图6所示,作点A 关于MN的对称点A',根据圆的对称性,点A'必在圆上;连接BA'交MN于点 P,连接PA,则PA+PB最小,此时 A'B;连接OA,OA',OB.
∴∠AON=∠A'ON=60°.
∵点B是 的中点,
∴∠A'OB=90°.
∵⊙O 的半径为1,
即AP+BP的最小值为
同课章节目录
