2025年中考数学几何解题方法复习--第2节 垂径定理(含解析)
文档属性
| 名称 | 2025年中考数学几何解题方法复习--第2节 垂径定理(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 399.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 21:51:31 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第2节 垂径定理
一、知识梳理
(一)垂径定理
垂直于弦的直径平分这条弦,并且平分弦所对的弧.
如图2-1所示,垂径定理的条件与结论理解如下:
∵AB 是直径,AB⊥CD于点 E,
(二)垂径定理推论
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.
【例】如图2-2所示,AB是⊙O 的弦,点 C,D 是直线AB上的两点,且AC=BD,求证:OC=OD.
证明:如图2-3所示,过点O 作OE⊥AB 于点E.
∵OE⊥AB,
∴AE=BE.
又∵AC=BD,
∴CE=DE.
∴OE是CD的中垂线.
∴OC=OD.
二、分层练习
1.下列判断中正确的是( ).
A.长度相等的弧是等弧
B.平分弦的直线也必平分弦所对的两条弧
C.弦的垂直平分线必平分弦所对的两条弧
D.平分一条弧的直线必平分这条弧所对的弦
2.某蔬菜基地的圆弧形蔬菜大棚的剖面如图2-4所示,已知AB=16m,半径OA为10m,则中间柱 CD的高度为( )m.
A. 6
B. 4
C. 8
D. 5
3. 如图2-5所示,点A,B是⊙O上的两点,AB=10,点 P 是⊙O上的动点(点P与点A,B不重合). 连接AP,PB,过点O分别作OE⊥AP 于点 E,OF⊥PB 于点 F,连接EF,则EF长为( ).
A. 4
B. 5
C. 5.5
D. 6
4.点P为⊙O内一点,且OP=4.若⊙O 的半径为6,则过点 P的弦长不可能为( ).
A. 12 C. 8 D. 10.5
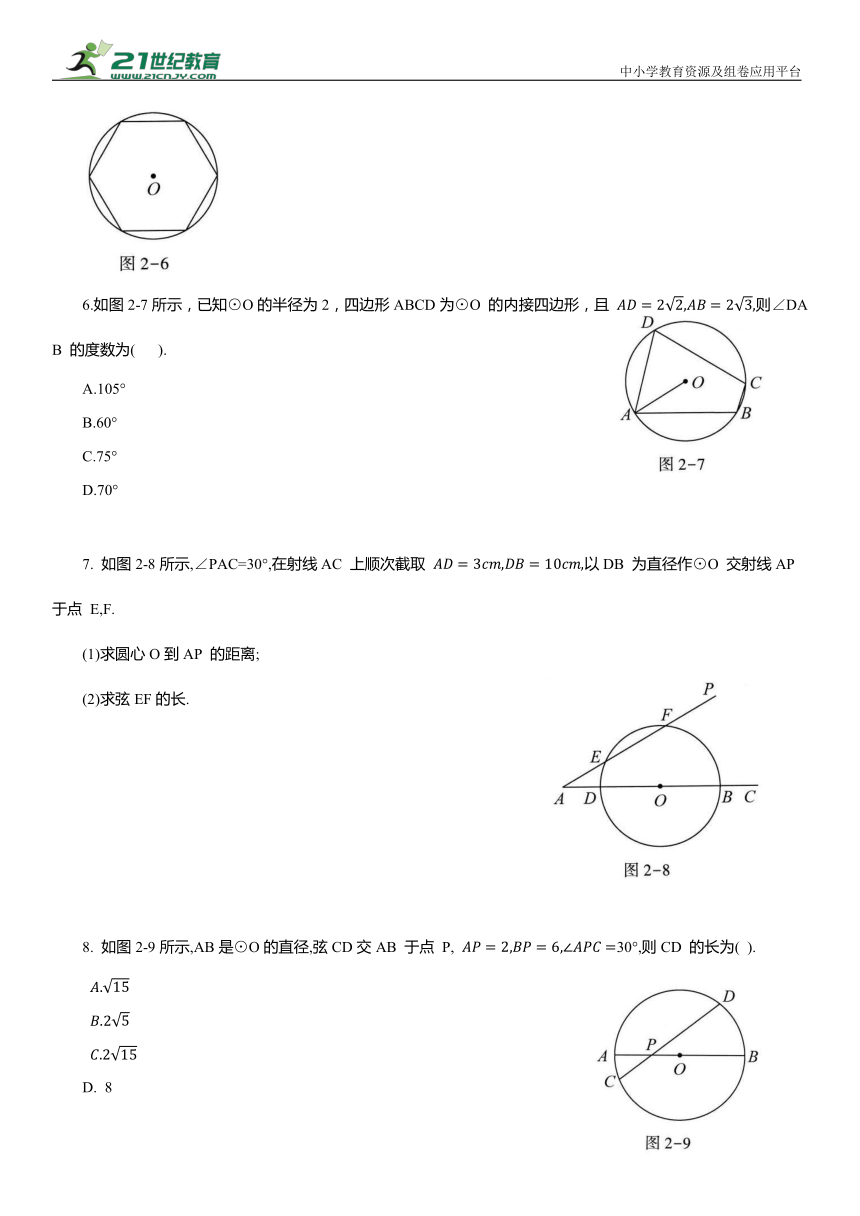
5.刘徽是中国古代卓越的数学家之一,他在《九章算术》中提出了“割圆术”,即用内接或外切正多边形逐步逼近圆来近似计算圆的面积.如图2-6所示,设⊙O的半径为2,若用⊙O的内接正六边形的面积来估计⊙O的面积,则⊙O的面积约为 (结果保留根号).
6.如图2-7所示,已知⊙O的半径为2,四边形ABCD为⊙O 的内接四边形,且 则∠DAB 的度数为( ).
A.105°
B.60°
C.75°
D.70°
7. 如图2-8所示,∠PAC=30°,在射线AC 上顺次截取 以DB 为直径作⊙O 交射线AP 于点 E,F.
(1)求圆心O到AP 的距离;
(2)求弦EF的长.
8. 如图2-9所示,AB是⊙O的直径,弦CD交AB 于点 P, 30°,则CD 的长为( ).
D. 8
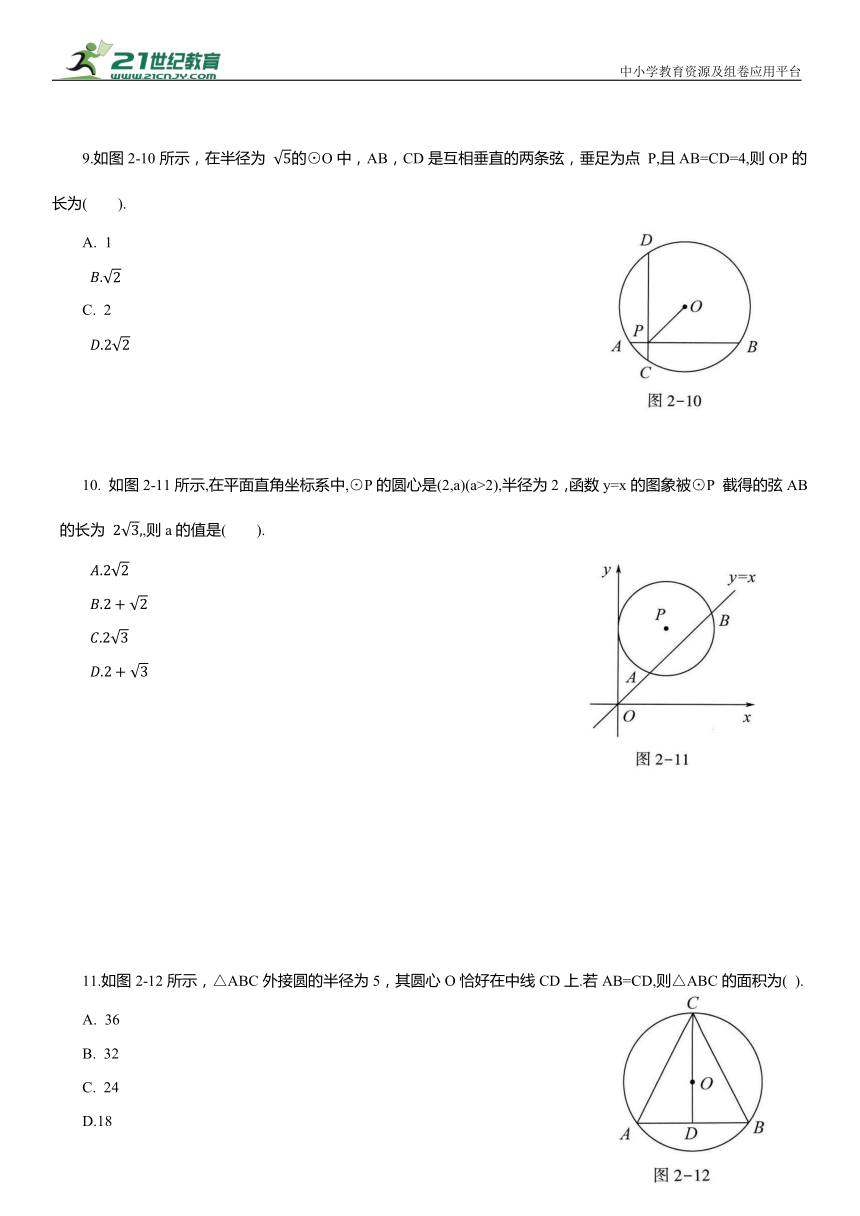
9.如图2-10所示,在半径为 的⊙O中,AB,CD是互相垂直的两条弦,垂足为点 P,且AB=CD=4,则OP的长为( ).
A. 1
C. 2
10. 如图2-11所示,在平面直角坐标系中,⊙P的圆心是(2,a)(a>2),半径为2,函数y=x的图象被⊙P 截得的弦AB 的长为 ,则a的值是( ).
11.如图2-12所示,△ABC外接圆的半径为5,其圆心O恰好在中线CD上.若AB=CD,则△ABC的面积为( ).
A. 36
B. 32
C. 24
D.18
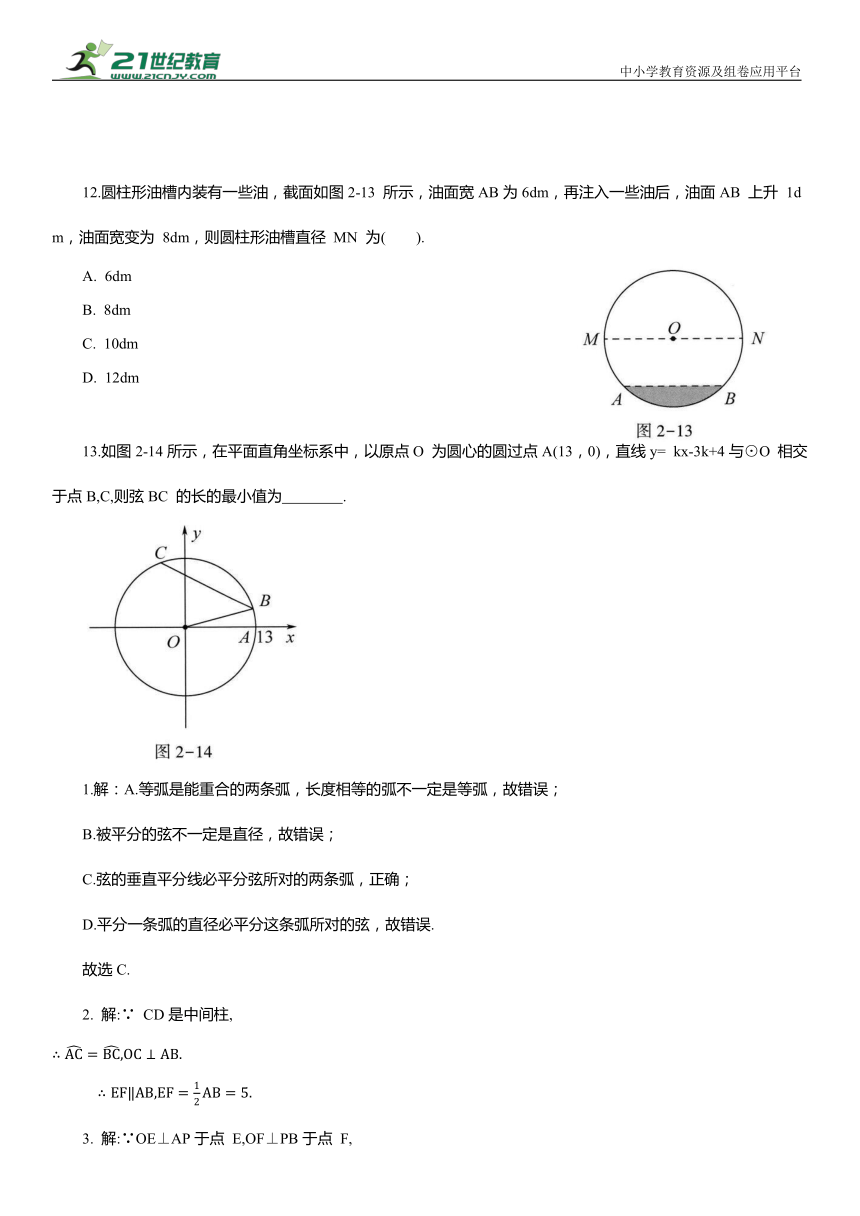
12.圆柱形油槽内装有一些油,截面如图2-13 所示,油面宽AB为6dm,再注入一些油后,油面AB 上升 1dm,油面宽变为 8dm,则圆柱形油槽直径 MN 为( ).
A. 6dm
B. 8dm
C. 10dm
D. 12dm
13.如图2-14所示,在平面直角坐标系中,以原点O 为圆心的圆过点A(13,0),直线y= kx-3k+4与⊙O 相交于点B,C,则弦BC 的长的最小值为 .
1.解:A.等弧是能重合的两条弧,长度相等的弧不一定是等弧,故错误;
B.被平分的弦不一定是直径,故错误;
C.弦的垂直平分线必平分弦所对的两条弧,正确;
D.平分一条弧的直径必平分这条弧所对的弦,故错误.
故选C.
2. 解:∵ CD是中间柱,
3. 解:∵OE⊥AP于点 E,OF⊥PB于点 F,
∴AE=PE,PF=BF.
∵半径OA为10m,
故选B.
CD=OC-OD=10-6=4(m).
故选 B.
4.解:如图7所示,过点 P作OP⊥AB,则AB是过点 P 最短的弦.
∵OP⊥AB,
∴AP=BP.
∵OP=4,⊙O的半径为6,
∴在 Rt△AOP中,
由于 所以过点P的弦长不可能为8.
故选C.
5. 解:如图8所示,连接OA,OB,过点O作OM⊥AB 于点 M.由题意可得,
∵OA=OB=2,
∴△OAB为等边三角形,AB=2.
∴AM=BM=1.
∴在Rt△AOM中,
∴⊙O的面积约为
6. 解:如图9所示,作OE⊥AB 于点 E,OF⊥AD 于点 F.
∵OE⊥AB,OF⊥AD,
∵在 Rt△AOE中,
∴∠OAE=30°.
∵在 Rt△AOF中,
∴∠OAF=45°.
∴ ∠DAB=∠OAE+∠OAF=30°+45°=75°.
故选C.
7. 解:(1)如图10所示,过点O 作 OH⊥EF 于点 H.
∵OB为⊙O的直径,且DB=10cm,
∴OD=5cm.
∴OA=OD+AD=3+5=8cm.
∵在 Rt△OAH中,∠OAH=30°,
即圆心O到AP 的距离为4cm.
(2)如图10所示,连接OF.
∵OH⊥EF,
∴EH=HF.
∵在Rt△OHF中,
∴EF=2HF=6(cm).
8. 解:如图11所示,作OH⊥CD于点H,连接OC.
∵OH⊥CD,
∴HC=HD.
∵AP=2,BP=6,
∴AB=8.
∴OA=4.
∴OP=OA-AP=2.
∵在 Rt△OPH中,∠OPH=∠APC=30°,
∵在 Rt△OHC中,OC=4,OH=1,
故选 C.
9. 解:如图12所示,作OE⊥AB 于点E,OF⊥CD 于点 F,连接OD,OB.
∵OE⊥AB,OF⊥CD,
∵在 Rt△OBE中,(
同理可得,OF=1.
∵AB⊥CD,OE=OF=1,
∴四边形OEPF为正方形.
故选 B.
10. 解:如图13所示,过点P作PE⊥AB于点E,PC⊥x轴于点 C,交AB于点 D,连接PA.
∵PE⊥AB,AB=2 ,(⊙P 的半径为2,
∴根据勾股定理得,
∵点A在直线y=x上,
∴ ∠AOC=45°.
∵∠DCO=90°,
∴∠ODC=45°.
∴△OCD 是等腰直角三角形,OC=DC=2.
∴ ∠PDE=∠ODC=45°.
∴∠DPE=∠PDE=45°.
∴DE=PE=1.
∵⊙P的圆心是(2,a),
故选 B.
11. 解:如图14所示,连接OA,OB,则OA=OB=OC=5.
∵圆心O 恰好在中线CD上,AB=2AD,
∴ CD⊥AB.
设AD=x,则CD=AB=2x,OD=CD-CO=2x-5.
∵在 Rt△OAD中, 即 解得 (舍去),
∴CD=AB=2x=8.
故选 B.
12.解:如图15所示,过点O作AB的垂线,垂足为点E,交CD 于点 F,连接OA,OC.
∵AB=6dm,CD=8dm,
∴由垂径定理得, 设OE= xdm,则OF=(x-1) dm.
∵在 Rt△OAE中,
在Rt△OCF中,
且OA=OC,
解得x=4.
∴直径MN=2OA=10(dm).
故选 C.
13. 解:∵直线y= kx-3k+4=k(x-3)+4,
∴直线必过点 D(3,4).
∴最短的弦BC是过点D且与该圆直径垂直的弦,如图16所示.
∵点D的坐标是(3,4),
∴OD=5.
∵以原点O 为圆心的圆过点A(13,0),
∴⊙O的半径为13.
∴OB=13.
∴ BC的长的最小值为24.
第2节 垂径定理
一、知识梳理
(一)垂径定理
垂直于弦的直径平分这条弦,并且平分弦所对的弧.
如图2-1所示,垂径定理的条件与结论理解如下:
∵AB 是直径,AB⊥CD于点 E,
(二)垂径定理推论
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.
【例】如图2-2所示,AB是⊙O 的弦,点 C,D 是直线AB上的两点,且AC=BD,求证:OC=OD.
证明:如图2-3所示,过点O 作OE⊥AB 于点E.
∵OE⊥AB,
∴AE=BE.
又∵AC=BD,
∴CE=DE.
∴OE是CD的中垂线.
∴OC=OD.
二、分层练习
1.下列判断中正确的是( ).
A.长度相等的弧是等弧
B.平分弦的直线也必平分弦所对的两条弧
C.弦的垂直平分线必平分弦所对的两条弧
D.平分一条弧的直线必平分这条弧所对的弦
2.某蔬菜基地的圆弧形蔬菜大棚的剖面如图2-4所示,已知AB=16m,半径OA为10m,则中间柱 CD的高度为( )m.
A. 6
B. 4
C. 8
D. 5
3. 如图2-5所示,点A,B是⊙O上的两点,AB=10,点 P 是⊙O上的动点(点P与点A,B不重合). 连接AP,PB,过点O分别作OE⊥AP 于点 E,OF⊥PB 于点 F,连接EF,则EF长为( ).
A. 4
B. 5
C. 5.5
D. 6
4.点P为⊙O内一点,且OP=4.若⊙O 的半径为6,则过点 P的弦长不可能为( ).
A. 12 C. 8 D. 10.5
5.刘徽是中国古代卓越的数学家之一,他在《九章算术》中提出了“割圆术”,即用内接或外切正多边形逐步逼近圆来近似计算圆的面积.如图2-6所示,设⊙O的半径为2,若用⊙O的内接正六边形的面积来估计⊙O的面积,则⊙O的面积约为 (结果保留根号).
6.如图2-7所示,已知⊙O的半径为2,四边形ABCD为⊙O 的内接四边形,且 则∠DAB 的度数为( ).
A.105°
B.60°
C.75°
D.70°
7. 如图2-8所示,∠PAC=30°,在射线AC 上顺次截取 以DB 为直径作⊙O 交射线AP 于点 E,F.
(1)求圆心O到AP 的距离;
(2)求弦EF的长.
8. 如图2-9所示,AB是⊙O的直径,弦CD交AB 于点 P, 30°,则CD 的长为( ).
D. 8
9.如图2-10所示,在半径为 的⊙O中,AB,CD是互相垂直的两条弦,垂足为点 P,且AB=CD=4,则OP的长为( ).
A. 1
C. 2
10. 如图2-11所示,在平面直角坐标系中,⊙P的圆心是(2,a)(a>2),半径为2,函数y=x的图象被⊙P 截得的弦AB 的长为 ,则a的值是( ).
11.如图2-12所示,△ABC外接圆的半径为5,其圆心O恰好在中线CD上.若AB=CD,则△ABC的面积为( ).
A. 36
B. 32
C. 24
D.18
12.圆柱形油槽内装有一些油,截面如图2-13 所示,油面宽AB为6dm,再注入一些油后,油面AB 上升 1dm,油面宽变为 8dm,则圆柱形油槽直径 MN 为( ).
A. 6dm
B. 8dm
C. 10dm
D. 12dm
13.如图2-14所示,在平面直角坐标系中,以原点O 为圆心的圆过点A(13,0),直线y= kx-3k+4与⊙O 相交于点B,C,则弦BC 的长的最小值为 .
1.解:A.等弧是能重合的两条弧,长度相等的弧不一定是等弧,故错误;
B.被平分的弦不一定是直径,故错误;
C.弦的垂直平分线必平分弦所对的两条弧,正确;
D.平分一条弧的直径必平分这条弧所对的弦,故错误.
故选C.
2. 解:∵ CD是中间柱,
3. 解:∵OE⊥AP于点 E,OF⊥PB于点 F,
∴AE=PE,PF=BF.
∵半径OA为10m,
故选B.
CD=OC-OD=10-6=4(m).
故选 B.
4.解:如图7所示,过点 P作OP⊥AB,则AB是过点 P 最短的弦.
∵OP⊥AB,
∴AP=BP.
∵OP=4,⊙O的半径为6,
∴在 Rt△AOP中,
由于 所以过点P的弦长不可能为8.
故选C.
5. 解:如图8所示,连接OA,OB,过点O作OM⊥AB 于点 M.由题意可得,
∵OA=OB=2,
∴△OAB为等边三角形,AB=2.
∴AM=BM=1.
∴在Rt△AOM中,
∴⊙O的面积约为
6. 解:如图9所示,作OE⊥AB 于点 E,OF⊥AD 于点 F.
∵OE⊥AB,OF⊥AD,
∵在 Rt△AOE中,
∴∠OAE=30°.
∵在 Rt△AOF中,
∴∠OAF=45°.
∴ ∠DAB=∠OAE+∠OAF=30°+45°=75°.
故选C.
7. 解:(1)如图10所示,过点O 作 OH⊥EF 于点 H.
∵OB为⊙O的直径,且DB=10cm,
∴OD=5cm.
∴OA=OD+AD=3+5=8cm.
∵在 Rt△OAH中,∠OAH=30°,
即圆心O到AP 的距离为4cm.
(2)如图10所示,连接OF.
∵OH⊥EF,
∴EH=HF.
∵在Rt△OHF中,
∴EF=2HF=6(cm).
8. 解:如图11所示,作OH⊥CD于点H,连接OC.
∵OH⊥CD,
∴HC=HD.
∵AP=2,BP=6,
∴AB=8.
∴OA=4.
∴OP=OA-AP=2.
∵在 Rt△OPH中,∠OPH=∠APC=30°,
∵在 Rt△OHC中,OC=4,OH=1,
故选 C.
9. 解:如图12所示,作OE⊥AB 于点E,OF⊥CD 于点 F,连接OD,OB.
∵OE⊥AB,OF⊥CD,
∵在 Rt△OBE中,(
同理可得,OF=1.
∵AB⊥CD,OE=OF=1,
∴四边形OEPF为正方形.
故选 B.
10. 解:如图13所示,过点P作PE⊥AB于点E,PC⊥x轴于点 C,交AB于点 D,连接PA.
∵PE⊥AB,AB=2 ,(⊙P 的半径为2,
∴根据勾股定理得,
∵点A在直线y=x上,
∴ ∠AOC=45°.
∵∠DCO=90°,
∴∠ODC=45°.
∴△OCD 是等腰直角三角形,OC=DC=2.
∴ ∠PDE=∠ODC=45°.
∴∠DPE=∠PDE=45°.
∴DE=PE=1.
∵⊙P的圆心是(2,a),
故选 B.
11. 解:如图14所示,连接OA,OB,则OA=OB=OC=5.
∵圆心O 恰好在中线CD上,AB=2AD,
∴ CD⊥AB.
设AD=x,则CD=AB=2x,OD=CD-CO=2x-5.
∵在 Rt△OAD中, 即 解得 (舍去),
∴CD=AB=2x=8.
故选 B.
12.解:如图15所示,过点O作AB的垂线,垂足为点E,交CD 于点 F,连接OA,OC.
∵AB=6dm,CD=8dm,
∴由垂径定理得, 设OE= xdm,则OF=(x-1) dm.
∵在 Rt△OAE中,
在Rt△OCF中,
且OA=OC,
解得x=4.
∴直径MN=2OA=10(dm).
故选 C.
13. 解:∵直线y= kx-3k+4=k(x-3)+4,
∴直线必过点 D(3,4).
∴最短的弦BC是过点D且与该圆直径垂直的弦,如图16所示.
∵点D的坐标是(3,4),
∴OD=5.
∵以原点O 为圆心的圆过点A(13,0),
∴⊙O的半径为13.
∴OB=13.
∴ BC的长的最小值为24.
同课章节目录
