2025年中考数学几何解题方法复习-- 第5节直线与圆的位置关系(含解析)
文档属性
| 名称 | 2025年中考数学几何解题方法复习-- 第5节直线与圆的位置关系(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 341.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 21:47:22 | ||
图片预览



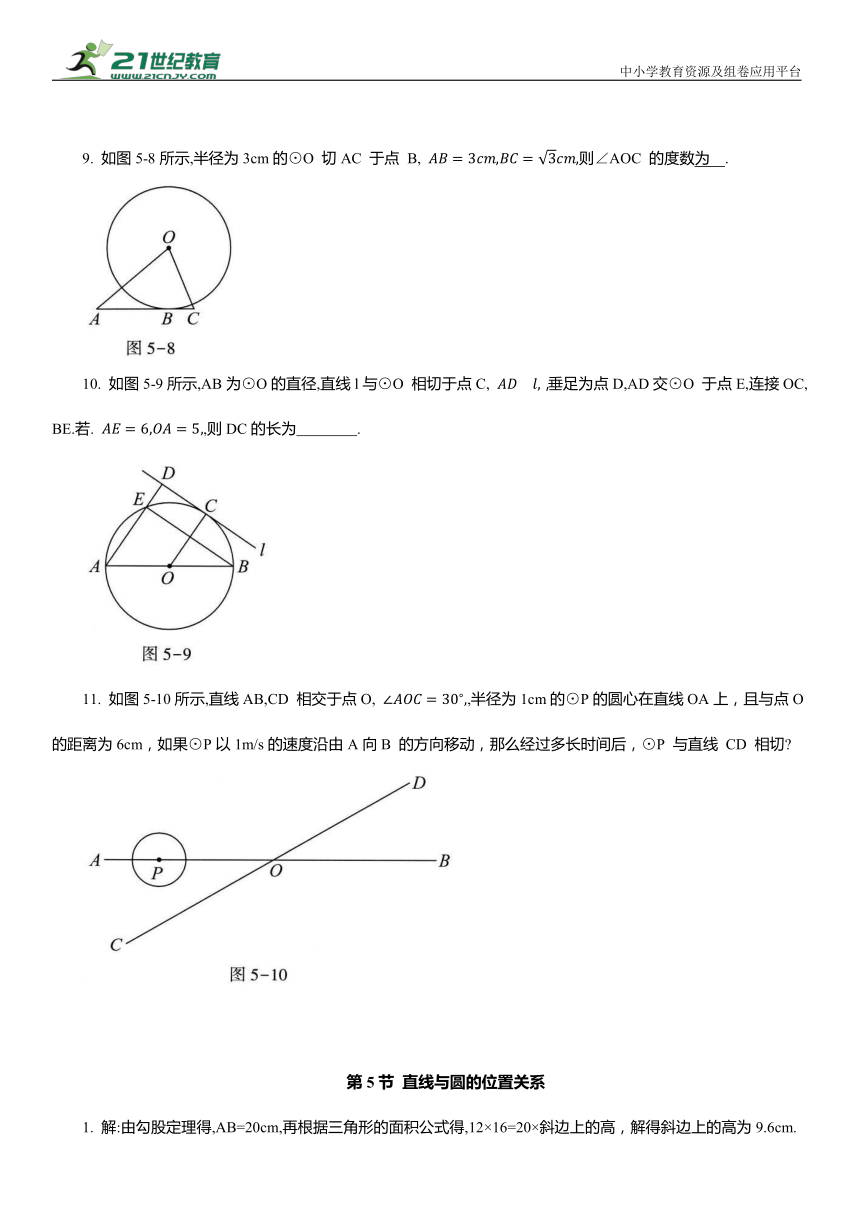
文档简介
中小学教育资源及组卷应用平台
第5节直线与圆的位置关系
一、知识梳理
(一)直线与圆的位置关系
设⊙O 的半径为r,圆心O到直线l的距离为d,则直线和圆的位置关系如表1所示.
表1 直线与圆的位置关系
位置关系 图形 定义 性质及判定
相离 直线与圆没有公共点 d>r 直线l与⊙O 相离
相切 直线与圆有唯一公共点,直线叫作圆的切线,唯一公共点叫作切点 d=r 直线l与⊙O 相切
相交 直线与圆有两个公共点,直线叫作圆的割线 d(二)切线的性质与判定
切线的性质:圆的切线垂直于过切点的半径.
切线的判定:过半径外端且垂直于半径的直线是圆的切线.
【例】如图5-1所示,BC 是半圆的直径,点D 是半圆上的一点,过点 D 作⊙O 的切线AD,BA⊥DA 于点A,交半圆于点 E. 已知 那么直线CE与以点O 为圆心, 为半径的圆的位置关系是( ).
A.相切 B.相交
C.相离 D.无法确定
解:如图5-2所示,连接OD 交CE于点 F,则OD⊥AD.
∵BA⊥DA,OD⊥AD,
∴OD∥AB.
∵OB=OC,
∴ CF=EF.
∴OD⊥CE.
∴四边形AEFD是矩形,CF=EF=AD=4.
在 Rt△OFC 中,根据勾股定理得
即圆心O到CE的距离大于以点O为圆心,
为半径的圆的半径,则直线和圆相离.
故选 C.
二、分层练习
1. 在Rt△ABC中,∠C=90°,AC=12cm,BC=16cm,以点C为圆心,r为半径的圆和AB有怎样的位置关系
(1)r=9cm;
(2)r=10cm;
(3)r=9.6cm.
2.在平面直角坐标系中,以点(3,4)为圆心,4为半径的圆( ).
A.与x轴相交,与y轴相切 B.与x轴相离,与y轴相交
C.与x轴相切,与y轴相交 D.与x轴相切,与y轴相离
3.以坐标原点O为圆心,作半径为2的圆.若直线y=-x+b与⊙O相交,则b的取值范围为( ).
4. 如图5-3所示,AB是⊙O的直径,AC与⊙O 相切于点A,BC交⊙O于点D.若∠C=70°,则∠AOD 的度数为( ).
A. 70°
B. 35°
C. 20°
D. 40°
5. 如图5-4所示,CD是⊙O的直径,CD=8,点A在CD的延长线上,AB与⊙O相切于点 B. 若∠A=30°,则AB= .
6. 如图5-5所示,AB是⊙O的直径,点P是⊙O外一点,PO交⊙O于点 C,连接BC,PA.若∠P=40°,当∠B=( )时,PA与⊙O相切.
A. 20°
B. 25°
C. 30°
D. 40°
7. 如图5-6所示,PA 和PB是⊙O的切线,点A,B是切点,AC是⊙O的直径.已知∠P=40°,则∠ACB的度数为( ).
A. 40°
B. 60°
C. 70°
D. 80°
8. 如图5-7所示,AB是⊙O 的直径,点 D 在AB 的延长线上,DC切⊙O 于点 C.若 则AC的长为( ).
A. 6
B. 4
D. 3
9. 如图5-8所示,半径为3cm的⊙O 切AC 于点 B, 则∠AOC 的度数为 .
10. 如图5-9所示,AB为⊙O的直径,直线l与⊙O 相切于点C, ,垂足为点D,AD交⊙O 于点E,连接OC,BE.若. ,则DC的长为 .
11. 如图5-10所示,直线AB,CD 相交于点O, ,半径为1cm的⊙P的圆心在直线OA上,且与点O的距离为6cm,如果⊙P以1m/s的速度沿由A向B 的方向移动,那么经过多长时间后,⊙P 与直线 CD 相切
第5节 直线与圆的位置关系
1. 解:由勾股定理得,AB=20cm,再根据三角形的面积公式得,12×16=20×斜边上的高,解得斜边上的高为9.6cm.
(1)∵r=9<9.6,∴⊙C与AB相离.
(2)∵r=10>9.6,∴⊙C与AB相交.
(3)∵r=9.6=9.6,∴⊙C与AB相切.
2. 解:∵圆心到x轴的距离是4,到y轴的距离是3,33.解:当直线y=-x+b与圆相切,且函数图象经过第一、第二、第四象限时,如图35所示.
∵在y=-x+b中,令x=0时,y=b,故直线与y轴的交点为B(0,b);
当y=0时,x=b,故点A的坐标为(b,0),
∴OA=OB,即△OAB 是等腰直角三角形.
连接圆心O和切点C,则OC=2.
同理,当直线y=-x+b与圆相切,且函数图象经过
第二、第三、第四象限时,
综上所述,若直线y=-x+b与⊙O相交,则b的取值范围为
故选 D.
4. 解:∵AC是⊙O 的切线,AB是⊙O 的直径,
∴AB⊥AC,∠CAB=90°.
又∵∠C=70°,
∴∠CBA=20°.
∴∠DOA=2∠CBA=40°.
故选 D.
5. 解:如图36所示,连接OB.
∵AB与⊙O 相切于点 B,
∴∠OBA=90°.
∵ CD是⊙O的直径,CD=8,
∴OB=4.
∵∠A=30°,
6. 解:∵ PA是⊙O 的切线,
∴∠PAO=90°.
∴∠AOP=90°-∠P=50°.
故选 B.
7. 解:如图37所示,连接OB.
∵AC是⊙O的直径,
∴∠ABC=90°.
∵ PA,PB是⊙O 的切线,点A,B为切点,
∴∠OAP=∠OBP=90°.
故选 C.
8. 解:如图38所示,连接OC.
∵DC切⊙O 于点 C,
∴OC⊥CD.
∵∠D=30°,
∴∠DOC=60°.
∵OA=OC,
∴∠OCA=∠OAC=30°.
∴∠D=∠OAC.
故选 C.
9. 解:如图39所示,连接OB,则OB⊥AC.
即∠AOB=45°,∠BOC=30°.
∴∠AOC=∠AOB+∠BOC=75°.
10. 解:OC交BE于点 F,如图40所示.
∵AB为⊙O 的直径,
∴∠AEB=90°.
∵AD⊥l,
∴BE∥CD.
∵直线l与⊙O相切于点 C,
∴OC⊥CD.
∴OC⊥BE.
∴四边形 CDEF 为矩形.
∴CD=EF.
∵在 Rt△ABE中,
∴BF=EF=4.
☆会当凌绝顶,一览众山小
11.解:如图41所示,⊙P 与直线 CD 相切,有两种情况.
① 当点P运动到 点时, 与CD相切,切点为点E,连接 则 CD.
∵ ⊙P 以 1cm/s 的速度由A 向B的方向移动,∴⊙P 到达( 需要的时间=4÷1=4(s).
∴经过4s后⊙P 与直线CD 相切.
②当点 P 运动到. 点时, 与CD 相切,则
∴⊙P 到达⊙P 需要的时间=8÷1=8(s).
∴经过8s后⊙P 与直线 CD 相切.
答:经过4s或8s后,⊙P与直线CD相切.
第5节直线与圆的位置关系
一、知识梳理
(一)直线与圆的位置关系
设⊙O 的半径为r,圆心O到直线l的距离为d,则直线和圆的位置关系如表1所示.
表1 直线与圆的位置关系
位置关系 图形 定义 性质及判定
相离 直线与圆没有公共点 d>r 直线l与⊙O 相离
相切 直线与圆有唯一公共点,直线叫作圆的切线,唯一公共点叫作切点 d=r 直线l与⊙O 相切
相交 直线与圆有两个公共点,直线叫作圆的割线 d
切线的性质:圆的切线垂直于过切点的半径.
切线的判定:过半径外端且垂直于半径的直线是圆的切线.
【例】如图5-1所示,BC 是半圆的直径,点D 是半圆上的一点,过点 D 作⊙O 的切线AD,BA⊥DA 于点A,交半圆于点 E. 已知 那么直线CE与以点O 为圆心, 为半径的圆的位置关系是( ).
A.相切 B.相交
C.相离 D.无法确定
解:如图5-2所示,连接OD 交CE于点 F,则OD⊥AD.
∵BA⊥DA,OD⊥AD,
∴OD∥AB.
∵OB=OC,
∴ CF=EF.
∴OD⊥CE.
∴四边形AEFD是矩形,CF=EF=AD=4.
在 Rt△OFC 中,根据勾股定理得
即圆心O到CE的距离大于以点O为圆心,
为半径的圆的半径,则直线和圆相离.
故选 C.
二、分层练习
1. 在Rt△ABC中,∠C=90°,AC=12cm,BC=16cm,以点C为圆心,r为半径的圆和AB有怎样的位置关系
(1)r=9cm;
(2)r=10cm;
(3)r=9.6cm.
2.在平面直角坐标系中,以点(3,4)为圆心,4为半径的圆( ).
A.与x轴相交,与y轴相切 B.与x轴相离,与y轴相交
C.与x轴相切,与y轴相交 D.与x轴相切,与y轴相离
3.以坐标原点O为圆心,作半径为2的圆.若直线y=-x+b与⊙O相交,则b的取值范围为( ).
4. 如图5-3所示,AB是⊙O的直径,AC与⊙O 相切于点A,BC交⊙O于点D.若∠C=70°,则∠AOD 的度数为( ).
A. 70°
B. 35°
C. 20°
D. 40°
5. 如图5-4所示,CD是⊙O的直径,CD=8,点A在CD的延长线上,AB与⊙O相切于点 B. 若∠A=30°,则AB= .
6. 如图5-5所示,AB是⊙O的直径,点P是⊙O外一点,PO交⊙O于点 C,连接BC,PA.若∠P=40°,当∠B=( )时,PA与⊙O相切.
A. 20°
B. 25°
C. 30°
D. 40°
7. 如图5-6所示,PA 和PB是⊙O的切线,点A,B是切点,AC是⊙O的直径.已知∠P=40°,则∠ACB的度数为( ).
A. 40°
B. 60°
C. 70°
D. 80°
8. 如图5-7所示,AB是⊙O 的直径,点 D 在AB 的延长线上,DC切⊙O 于点 C.若 则AC的长为( ).
A. 6
B. 4
D. 3
9. 如图5-8所示,半径为3cm的⊙O 切AC 于点 B, 则∠AOC 的度数为 .
10. 如图5-9所示,AB为⊙O的直径,直线l与⊙O 相切于点C, ,垂足为点D,AD交⊙O 于点E,连接OC,BE.若. ,则DC的长为 .
11. 如图5-10所示,直线AB,CD 相交于点O, ,半径为1cm的⊙P的圆心在直线OA上,且与点O的距离为6cm,如果⊙P以1m/s的速度沿由A向B 的方向移动,那么经过多长时间后,⊙P 与直线 CD 相切
第5节 直线与圆的位置关系
1. 解:由勾股定理得,AB=20cm,再根据三角形的面积公式得,12×16=20×斜边上的高,解得斜边上的高为9.6cm.
(1)∵r=9<9.6,∴⊙C与AB相离.
(2)∵r=10>9.6,∴⊙C与AB相交.
(3)∵r=9.6=9.6,∴⊙C与AB相切.
2. 解:∵圆心到x轴的距离是4,到y轴的距离是3,3
∵在y=-x+b中,令x=0时,y=b,故直线与y轴的交点为B(0,b);
当y=0时,x=b,故点A的坐标为(b,0),
∴OA=OB,即△OAB 是等腰直角三角形.
连接圆心O和切点C,则OC=2.
同理,当直线y=-x+b与圆相切,且函数图象经过
第二、第三、第四象限时,
综上所述,若直线y=-x+b与⊙O相交,则b的取值范围为
故选 D.
4. 解:∵AC是⊙O 的切线,AB是⊙O 的直径,
∴AB⊥AC,∠CAB=90°.
又∵∠C=70°,
∴∠CBA=20°.
∴∠DOA=2∠CBA=40°.
故选 D.
5. 解:如图36所示,连接OB.
∵AB与⊙O 相切于点 B,
∴∠OBA=90°.
∵ CD是⊙O的直径,CD=8,
∴OB=4.
∵∠A=30°,
6. 解:∵ PA是⊙O 的切线,
∴∠PAO=90°.
∴∠AOP=90°-∠P=50°.
故选 B.
7. 解:如图37所示,连接OB.
∵AC是⊙O的直径,
∴∠ABC=90°.
∵ PA,PB是⊙O 的切线,点A,B为切点,
∴∠OAP=∠OBP=90°.
故选 C.
8. 解:如图38所示,连接OC.
∵DC切⊙O 于点 C,
∴OC⊥CD.
∵∠D=30°,
∴∠DOC=60°.
∵OA=OC,
∴∠OCA=∠OAC=30°.
∴∠D=∠OAC.
故选 C.
9. 解:如图39所示,连接OB,则OB⊥AC.
即∠AOB=45°,∠BOC=30°.
∴∠AOC=∠AOB+∠BOC=75°.
10. 解:OC交BE于点 F,如图40所示.
∵AB为⊙O 的直径,
∴∠AEB=90°.
∵AD⊥l,
∴BE∥CD.
∵直线l与⊙O相切于点 C,
∴OC⊥CD.
∴OC⊥BE.
∴四边形 CDEF 为矩形.
∴CD=EF.
∵在 Rt△ABE中,
∴BF=EF=4.
☆会当凌绝顶,一览众山小
11.解:如图41所示,⊙P 与直线 CD 相切,有两种情况.
① 当点P运动到 点时, 与CD相切,切点为点E,连接 则 CD.
∵ ⊙P 以 1cm/s 的速度由A 向B的方向移动,∴⊙P 到达( 需要的时间=4÷1=4(s).
∴经过4s后⊙P 与直线CD 相切.
②当点 P 运动到. 点时, 与CD 相切,则
∴⊙P 到达⊙P 需要的时间=8÷1=8(s).
∴经过8s后⊙P 与直线 CD 相切.
答:经过4s或8s后,⊙P与直线CD相切.
同课章节目录
