2025年中考数学几何解题方法复习-- 第6节 切线的计算与证明(含解析)
文档属性
| 名称 | 2025年中考数学几何解题方法复习-- 第6节 切线的计算与证明(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 426.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 21:45:12 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第6节 切线的计算与证明
一、知识梳理
切线的性质:圆的切线垂直于过切点的半径.
切线的判定:过半径外端且垂直于半径的直线是圆的切线.
【例】如图6-1所示,点 C在以AB为直径的⊙O上,AD与过点 C 的切线垂直,垂足为点 D,AD 交⊙O 于点 E.
(1)求证:AC平分∠DAB;
(2)若AD=4,AC=5,求⊙O的半径;
(3)若AE=5,AB=13,求AC的长.
证明:(1)如图6-2所示,连接OC.
∵AO=CO,
∴ ∠ACO=∠CAO.
∵CD与⊙O 相切于点C,
∴CO⊥CD.
又∵AD⊥CD,
∴AD∥CO.
∴ ∠DAC=∠ACO.
∴ ∠DAC=∠CAO.
∴AC平分∠DAB.
(2)如图6-3所示,过点O 作OF⊥AC 于点 F.
∵AC=5,
∵∠CAO=∠DAC,∠AFO=∠ADC=90°,
∴△AFO∽△ADC.
即
∴AO=3.125,即⊙O 的半径为3.125.
(3)如图6-4所示,连接BE,OC,相交于点G.
∵AB 是⊙O的直径,
∴BE⊥AD.
∵DC是⊙O的切线,
∴DC⊥CO.
∴四边形ECGD 是矩形.
∴DE=CG,DC=EG,OC⊥BE.
∴DC=EG=6.
∴AD=AE+DE=9.
二、分层练习
1. 如图6-5所示,在△ABC中,AB=BC,以AB为直径的⊙O 交AC于点D,过点D作DF⊥BC,交AB 的延长线于点 E,垂足为点 F. 求证:直线DE 是⊙O的切线.
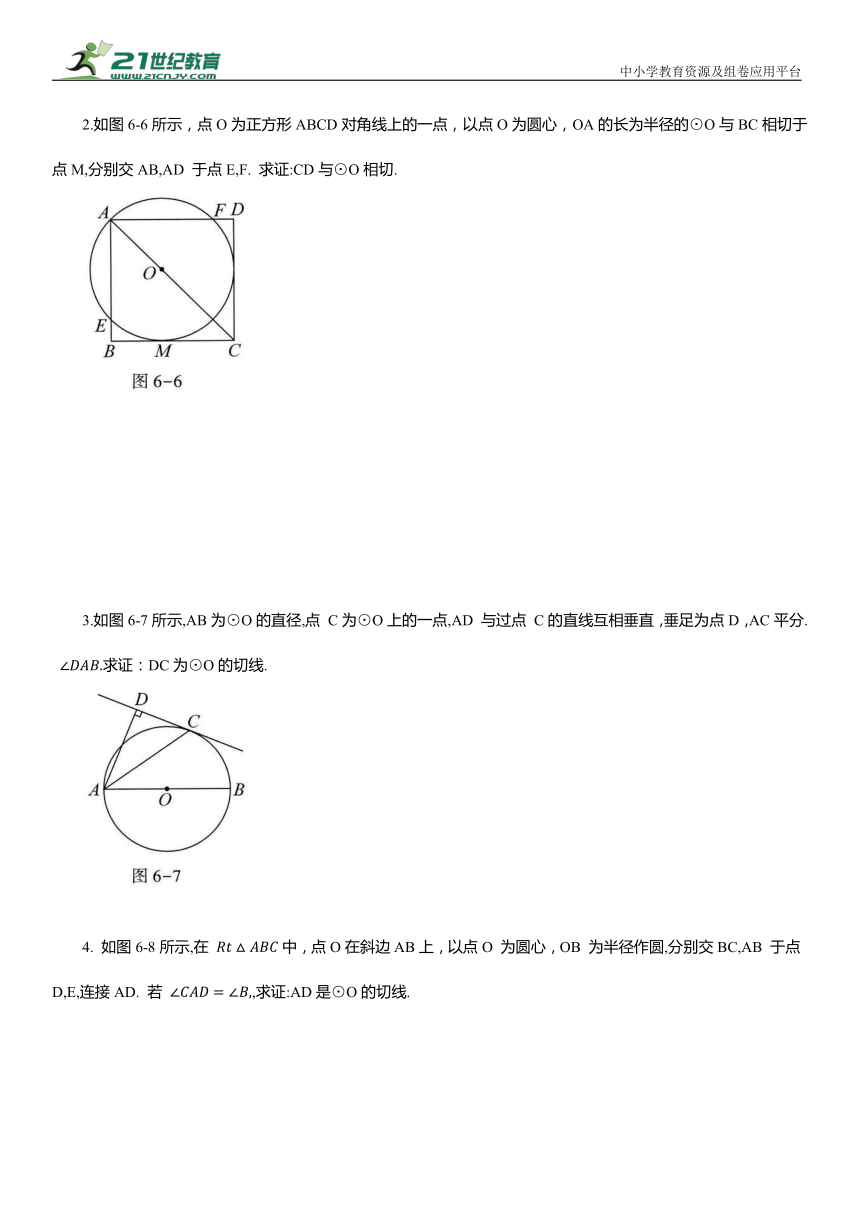
2.如图6-6所示,点O为正方形ABCD对角线上的一点,以点O为圆心,OA的长为半径的⊙O与BC相切于点M,分别交AB,AD 于点E,F. 求证:CD与⊙O相切.
3.如图6-7所示,AB为⊙O的直径,点 C为⊙O上的一点,AD 与过点 C的直线互相垂直,垂足为点D,AC平分. 求证:DC为⊙O的切线.
4. 如图6-8所示,在 中,点O在斜边AB上,以点O 为圆心,OB 为半径作圆,分别交BC,AB 于点 D,E,连接AD. 若 ,求证:AD是⊙O的切线.
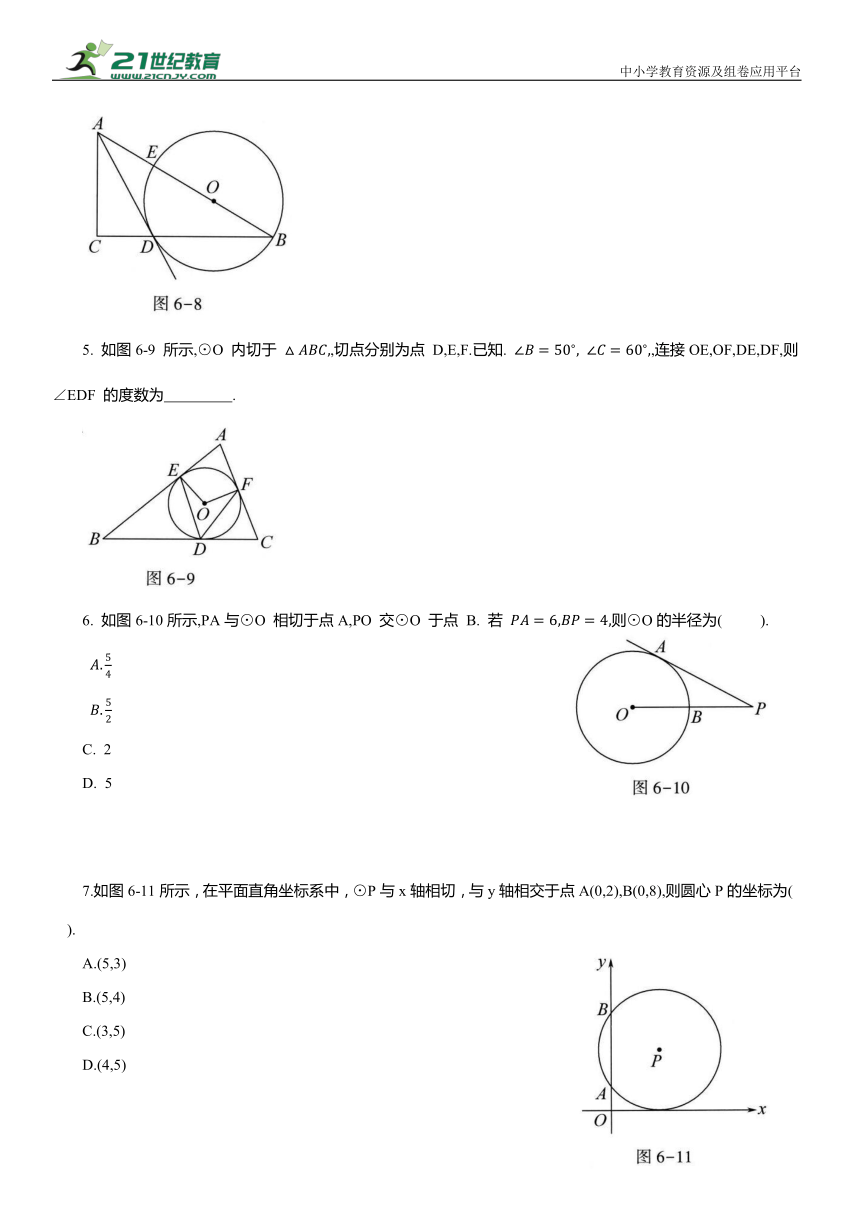
5. 如图6-9 所示,⊙O 内切于 ,切点分别为点 D,E,F.已知. ,连接OE,OF,DE,DF,则∠EDF 的度数为 .
6. 如图6-10所示,PA与⊙O 相切于点A,PO 交⊙O 于点 B. 若 则⊙O的半径为( ).
C. 2
D. 5
7.如图6-11所示,在平面直角坐标系中,⊙P与x轴相切,与y轴相交于点A(0,2),B(0,8),则圆心P的坐标为( ).
A.(5,3)
B.(5,4)
C.(3,5)
D.(4,5)
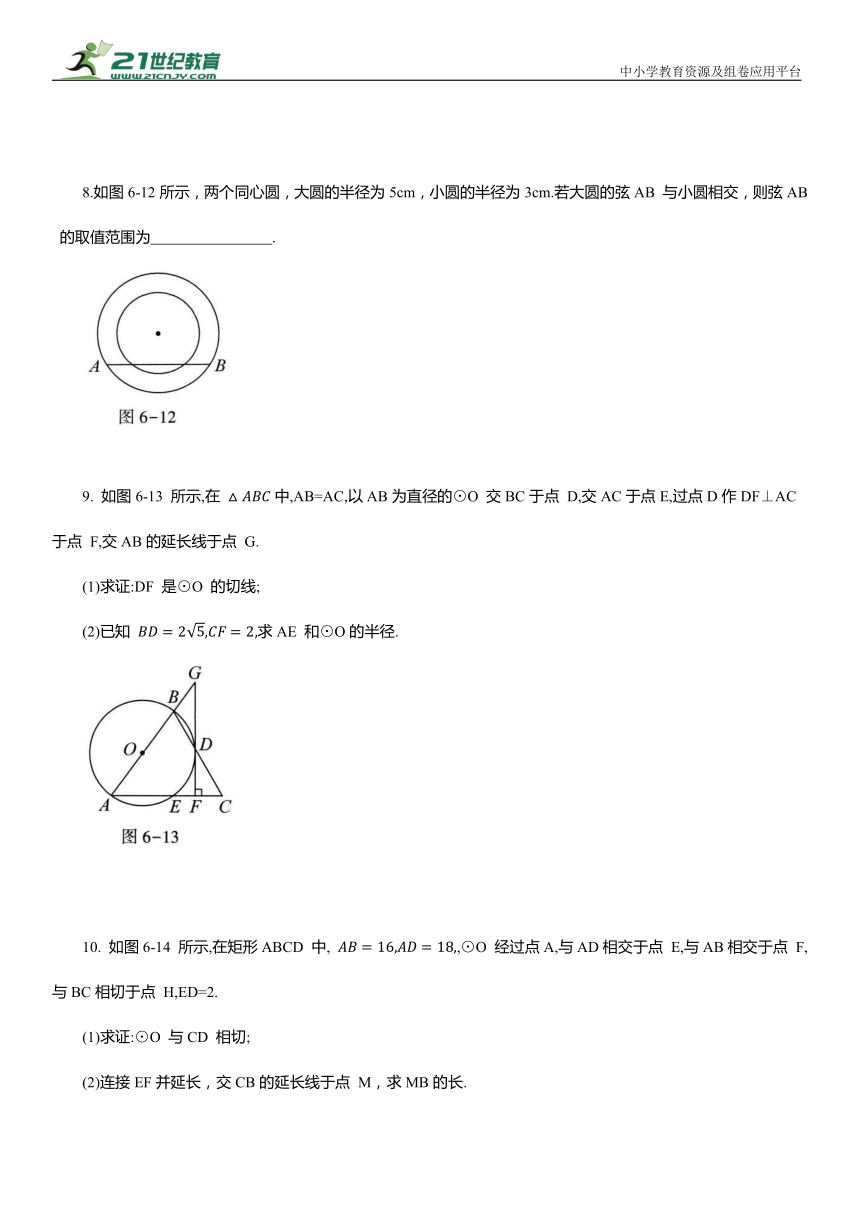
8.如图6-12所示,两个同心圆,大圆的半径为5cm,小圆的半径为3cm.若大圆的弦AB 与小圆相交,则弦AB 的取值范围为 .
9. 如图6-13 所示,在 中,AB=AC,以AB为直径的⊙O 交BC于点 D,交AC于点E,过点D作DF⊥AC于点 F,交AB的延长线于点 G.
(1)求证:DF 是⊙O 的切线;
(2)已知 求AE 和⊙O的半径.
10. 如图6-14 所示,在矩形ABCD 中, ,⊙O 经过点A,与AD相交于点 E,与AB相交于点 F,与BC相切于点 H,ED=2.
(1)求证:⊙O 与CD 相切;
(2)连接EF并延长,交CB的延长线于点 M,求MB的长.
第6节 切线的计算与证明
1. 证明:连接OD,如图42所示.
∵BA=BC,
∴∠A=∠C.
∵OA=OD,
∴∠A=∠ODA.
∴∠ODA=∠C.
∴OD∥BC.
∵DF⊥BC,
∴DE⊥OD.
∴直线DE是⊙O 的切线.
2. 证明:如图43所示,连接OM,过点O 作ON⊥CD,垂足为点 N.
∵⊙O与BC相切于点 M,
∴OM⊥BC.
∵四边形ABCD 是正方形,
∴AC平分∠BCD.
∴OM=ON.
∴ CD与⊙O 相切.
3. 证明:如图45所示,连接OC.
∵AC平分∠DAB,
∴∠DAC=∠BAC.
∵OA=OC,
∴∠BAC=∠ACO.
∴ ∠DAC=∠ACO.
∵AD⊥DC,
∴OC⊥DC.
∴DC为⊙O 的切线.
4. 证明:连接OD,∠1、∠2、∠3如图46所示.
∵OB=OD,
∴∠3=∠B.
∵∠B=∠1,
∴∠1=∠3.
∵在 Rt△ACD中,∠1+∠2=90°,
∴∠2+∠3=90°.
∴OD⊥AD,则AD为⊙O 的切线.
5. 解:∵∠A+∠B+∠C=180°,∠B=50°,∠C=60°,
∴∠A=70°.
∵⊙O 内切于△ABC,切点分别为点 D,E,F,
∴∠OEA=∠OFA=90°.
.
6. 解:如图47所示,连接OA,设OA=x.
∵PA与⊙O 相切于点A,
∴∠OAP=90°.
∴在 Rt△OAP中,
∵ PA=6,BP=4,
解得
故选B.
7. 解:如图48所示,过点P作PC⊥AB于点C,过点P作PD⊥x轴于点D,连接PB.
∵点A(0,2),B(0,8),
∴AB=8-2=6.
∵PC⊥AB,
∴AC=BC=3.
∴OC=8-3=5.
∵⊙P 与x轴相切,
∴PD=PB=OC=5,
在Rt△PBC中,由勾股定理可得
∴圆心P的坐标为(4,5).
故选 D.
8.解:如图49 所示,当AB 与小圆相切时有一个公共点D,连接OA,OD,可得OD⊥AB.
∵OD⊥AB,
∴点D为AB的中点,即AD=BD.
∵在Rt△ADO中,(
∴AD=4cm.
∴AB=2AD=8cm.
当AB经过同心圆的圆心时,即. ,满足弦AB与小圆相交,AB 最大,此时AB=10cm.
故AB 的取值范围为8cm9.(1)证明:如图50所示,连接OD,AD.
∵AB为⊙O 的直径,
,即AD⊥BC.
又∵
∵OD 是⊙O的半径,
∴直线DF与⊙O 相切.
(2)解:如图51所示,连接BE.
∵CF=2,
∵AB 是⊙O的直径,
∴∠AEB=∠CEB=90°.
∴BE⊥AC.
∵DF⊥AC,
∴DF∥BE.
∵ 点 D 为BC的中点,
∴DF是△BEC的中位线.
∴EF=FC=2.
∴BE=2DF=8.
设⊙O的半径长为r,则有AC=AB=2r,AE=2r-4.
∵在 Rt△ABE中,
解得r=5.
∴AE=6,⊙O的半径长为5.
10.(1)证明:如图52所示,过点O作OG⊥CD于点G,连接HO并延长,交AD于点 N.
∵四边形ABCD 是矩形,AB=16,AD=18,
∴CD=AB=16,BC=AD=18,∠A=∠ABC=∠C=∠CDA=90°,AD∥BC.
∵ED=2,
∴AE=AD-ED=16.
∵OG⊥CD,
∴∠OGD=∠OGC=90°.
∵BC与⊙O 相切于点 H,
∴OH⊥BC.
∵AD∥BC,
∴ON⊥AD.
∴四边形ABHN,OGCH,OGDN都是矩形.
∴BH=AN=8,HN=AB=16.
∴OG=HC=BC-BH=18-8=10.
∵在Rt△OEN中,ON=HN-OH=16-OH,OE=OH,根据勾股定理得
解得OH=10.
∴ ⊙O 的半径为10.
∵OG⊥CD,且OG是⊙O 的半径,
∴⊙O 与CD相切.
(2)解:∵⊙O 的半径为10,∠A=90°,
∴EF是⊙O 的直径,EF=20.
∵AE=16,
∴BF=AB-AF=16-12=4.
∵∠AFE=∠MFB,∠A=∠FBM=90°,
∴ △AFE∽△BFM.
即 解得
第6节 切线的计算与证明
一、知识梳理
切线的性质:圆的切线垂直于过切点的半径.
切线的判定:过半径外端且垂直于半径的直线是圆的切线.
【例】如图6-1所示,点 C在以AB为直径的⊙O上,AD与过点 C 的切线垂直,垂足为点 D,AD 交⊙O 于点 E.
(1)求证:AC平分∠DAB;
(2)若AD=4,AC=5,求⊙O的半径;
(3)若AE=5,AB=13,求AC的长.
证明:(1)如图6-2所示,连接OC.
∵AO=CO,
∴ ∠ACO=∠CAO.
∵CD与⊙O 相切于点C,
∴CO⊥CD.
又∵AD⊥CD,
∴AD∥CO.
∴ ∠DAC=∠ACO.
∴ ∠DAC=∠CAO.
∴AC平分∠DAB.
(2)如图6-3所示,过点O 作OF⊥AC 于点 F.
∵AC=5,
∵∠CAO=∠DAC,∠AFO=∠ADC=90°,
∴△AFO∽△ADC.
即
∴AO=3.125,即⊙O 的半径为3.125.
(3)如图6-4所示,连接BE,OC,相交于点G.
∵AB 是⊙O的直径,
∴BE⊥AD.
∵DC是⊙O的切线,
∴DC⊥CO.
∴四边形ECGD 是矩形.
∴DE=CG,DC=EG,OC⊥BE.
∴DC=EG=6.
∴AD=AE+DE=9.
二、分层练习
1. 如图6-5所示,在△ABC中,AB=BC,以AB为直径的⊙O 交AC于点D,过点D作DF⊥BC,交AB 的延长线于点 E,垂足为点 F. 求证:直线DE 是⊙O的切线.
2.如图6-6所示,点O为正方形ABCD对角线上的一点,以点O为圆心,OA的长为半径的⊙O与BC相切于点M,分别交AB,AD 于点E,F. 求证:CD与⊙O相切.
3.如图6-7所示,AB为⊙O的直径,点 C为⊙O上的一点,AD 与过点 C的直线互相垂直,垂足为点D,AC平分. 求证:DC为⊙O的切线.
4. 如图6-8所示,在 中,点O在斜边AB上,以点O 为圆心,OB 为半径作圆,分别交BC,AB 于点 D,E,连接AD. 若 ,求证:AD是⊙O的切线.
5. 如图6-9 所示,⊙O 内切于 ,切点分别为点 D,E,F.已知. ,连接OE,OF,DE,DF,则∠EDF 的度数为 .
6. 如图6-10所示,PA与⊙O 相切于点A,PO 交⊙O 于点 B. 若 则⊙O的半径为( ).
C. 2
D. 5
7.如图6-11所示,在平面直角坐标系中,⊙P与x轴相切,与y轴相交于点A(0,2),B(0,8),则圆心P的坐标为( ).
A.(5,3)
B.(5,4)
C.(3,5)
D.(4,5)
8.如图6-12所示,两个同心圆,大圆的半径为5cm,小圆的半径为3cm.若大圆的弦AB 与小圆相交,则弦AB 的取值范围为 .
9. 如图6-13 所示,在 中,AB=AC,以AB为直径的⊙O 交BC于点 D,交AC于点E,过点D作DF⊥AC于点 F,交AB的延长线于点 G.
(1)求证:DF 是⊙O 的切线;
(2)已知 求AE 和⊙O的半径.
10. 如图6-14 所示,在矩形ABCD 中, ,⊙O 经过点A,与AD相交于点 E,与AB相交于点 F,与BC相切于点 H,ED=2.
(1)求证:⊙O 与CD 相切;
(2)连接EF并延长,交CB的延长线于点 M,求MB的长.
第6节 切线的计算与证明
1. 证明:连接OD,如图42所示.
∵BA=BC,
∴∠A=∠C.
∵OA=OD,
∴∠A=∠ODA.
∴∠ODA=∠C.
∴OD∥BC.
∵DF⊥BC,
∴DE⊥OD.
∴直线DE是⊙O 的切线.
2. 证明:如图43所示,连接OM,过点O 作ON⊥CD,垂足为点 N.
∵⊙O与BC相切于点 M,
∴OM⊥BC.
∵四边形ABCD 是正方形,
∴AC平分∠BCD.
∴OM=ON.
∴ CD与⊙O 相切.
3. 证明:如图45所示,连接OC.
∵AC平分∠DAB,
∴∠DAC=∠BAC.
∵OA=OC,
∴∠BAC=∠ACO.
∴ ∠DAC=∠ACO.
∵AD⊥DC,
∴OC⊥DC.
∴DC为⊙O 的切线.
4. 证明:连接OD,∠1、∠2、∠3如图46所示.
∵OB=OD,
∴∠3=∠B.
∵∠B=∠1,
∴∠1=∠3.
∵在 Rt△ACD中,∠1+∠2=90°,
∴∠2+∠3=90°.
∴OD⊥AD,则AD为⊙O 的切线.
5. 解:∵∠A+∠B+∠C=180°,∠B=50°,∠C=60°,
∴∠A=70°.
∵⊙O 内切于△ABC,切点分别为点 D,E,F,
∴∠OEA=∠OFA=90°.
.
6. 解:如图47所示,连接OA,设OA=x.
∵PA与⊙O 相切于点A,
∴∠OAP=90°.
∴在 Rt△OAP中,
∵ PA=6,BP=4,
解得
故选B.
7. 解:如图48所示,过点P作PC⊥AB于点C,过点P作PD⊥x轴于点D,连接PB.
∵点A(0,2),B(0,8),
∴AB=8-2=6.
∵PC⊥AB,
∴AC=BC=3.
∴OC=8-3=5.
∵⊙P 与x轴相切,
∴PD=PB=OC=5,
在Rt△PBC中,由勾股定理可得
∴圆心P的坐标为(4,5).
故选 D.
8.解:如图49 所示,当AB 与小圆相切时有一个公共点D,连接OA,OD,可得OD⊥AB.
∵OD⊥AB,
∴点D为AB的中点,即AD=BD.
∵在Rt△ADO中,(
∴AD=4cm.
∴AB=2AD=8cm.
当AB经过同心圆的圆心时,即. ,满足弦AB与小圆相交,AB 最大,此时AB=10cm.
故AB 的取值范围为8cm
∵AB为⊙O 的直径,
,即AD⊥BC.
又∵
∵OD 是⊙O的半径,
∴直线DF与⊙O 相切.
(2)解:如图51所示,连接BE.
∵CF=2,
∵AB 是⊙O的直径,
∴∠AEB=∠CEB=90°.
∴BE⊥AC.
∵DF⊥AC,
∴DF∥BE.
∵ 点 D 为BC的中点,
∴DF是△BEC的中位线.
∴EF=FC=2.
∴BE=2DF=8.
设⊙O的半径长为r,则有AC=AB=2r,AE=2r-4.
∵在 Rt△ABE中,
解得r=5.
∴AE=6,⊙O的半径长为5.
10.(1)证明:如图52所示,过点O作OG⊥CD于点G,连接HO并延长,交AD于点 N.
∵四边形ABCD 是矩形,AB=16,AD=18,
∴CD=AB=16,BC=AD=18,∠A=∠ABC=∠C=∠CDA=90°,AD∥BC.
∵ED=2,
∴AE=AD-ED=16.
∵OG⊥CD,
∴∠OGD=∠OGC=90°.
∵BC与⊙O 相切于点 H,
∴OH⊥BC.
∵AD∥BC,
∴ON⊥AD.
∴四边形ABHN,OGCH,OGDN都是矩形.
∴BH=AN=8,HN=AB=16.
∴OG=HC=BC-BH=18-8=10.
∵在Rt△OEN中,ON=HN-OH=16-OH,OE=OH,根据勾股定理得
解得OH=10.
∴ ⊙O 的半径为10.
∵OG⊥CD,且OG是⊙O 的半径,
∴⊙O 与CD相切.
(2)解:∵⊙O 的半径为10,∠A=90°,
∴EF是⊙O 的直径,EF=20.
∵AE=16,
∴BF=AB-AF=16-12=4.
∵∠AFE=∠MFB,∠A=∠FBM=90°,
∴ △AFE∽△BFM.
即 解得
同课章节目录
