2025年中考数学几何解题方法复习-- 第 7 节 切线长定理(含解析)
文档属性
| 名称 | 2025年中考数学几何解题方法复习-- 第 7 节 切线长定理(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 311.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第 7 节 切线长定理
一、知识梳理
切线长定理:从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.
如图7-1所示,过⊙O外一点 P 可引两条切线 PA,PB,则PA=PB,PO平分∠APB.
【例1】如图 7-2所示,若△ABC 的三边长分别为AB=9,BC=5,CA=6,△ABC的内切圆⊙O 与AB,BC,AC 相切于点 D,E,F,则AF 的长为( ).
A. 5 B. 10
C. 7.5 D.4
解:设AF=x.
∵根据切线长定理得,AD=AF=x,
BE=BD=9-x,CE=CF=6-x,
∴则有9-x+6-x=5,解得x=5,即AF的长为5.
故选A.
二、分层练习
万丈高楼平地起
1. 如图7-3所示,PA,PB为⊙O 的切线,切点分别为点A,B,PO交AB 于点 C,PO的延长线交⊙O 于点 D,下列结论不一定成立的是( ).
A. PA=PB
B.∠BPD=∠APD
C. AB⊥PD
D. AB平分PD
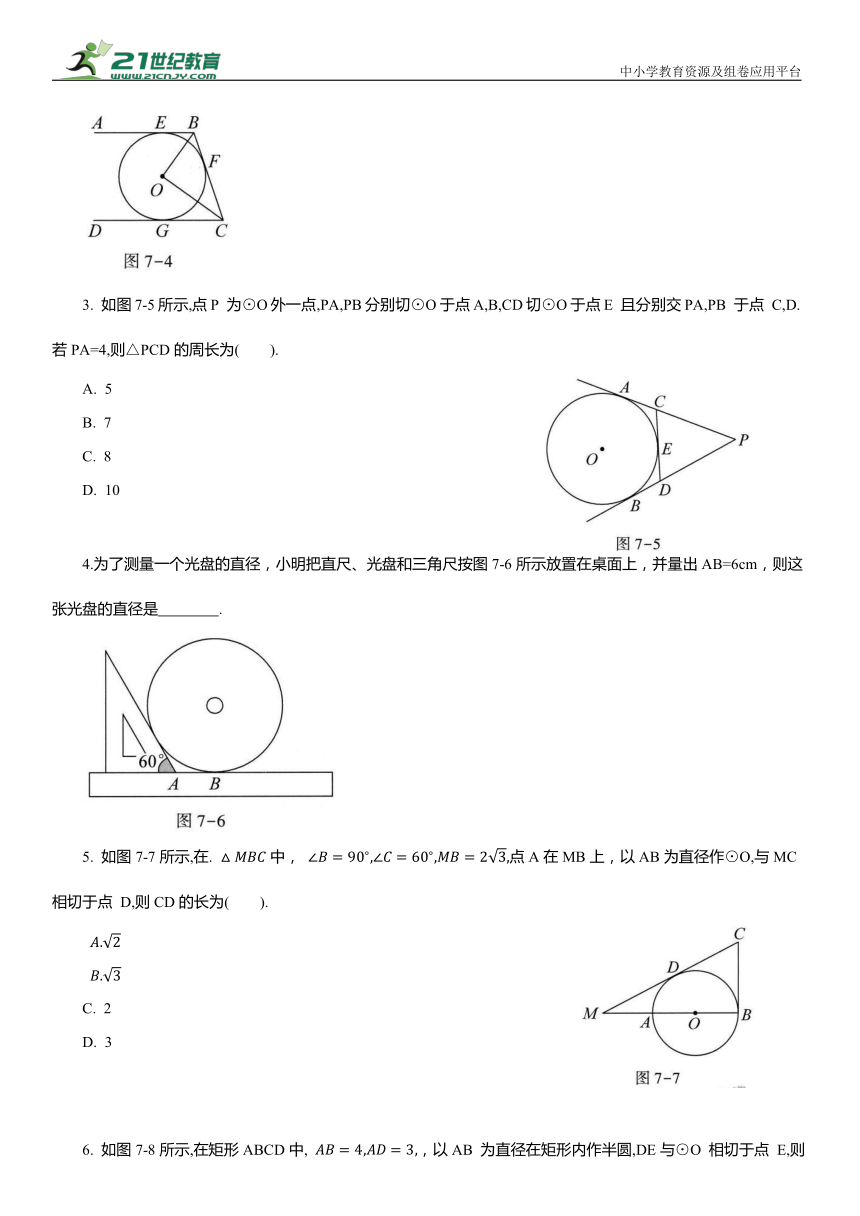
2. 如图7-4所示,直线AB,BC,CD分别与⊙O 相切于点E,F,G,且 若OB=6cm,OC=8cm,则BE+CG的长为 .
3. 如图7-5所示,点P 为⊙O外一点,PA,PB分别切⊙O于点A,B,CD切⊙O于点E 且分别交PA,PB 于点 C,D. 若PA=4,则△PCD的周长为( ).
A. 5
B. 7
C. 8
D. 10
4.为了测量一个光盘的直径,小明把直尺、光盘和三角尺按图7-6所示放置在桌面上,并量出AB=6cm,则这张光盘的直径是 .
5. 如图7-7所示,在. 中, 点A在MB上,以AB为直径作⊙O,与MC相切于点 D,则CD的长为( ).
C. 2
D. 3
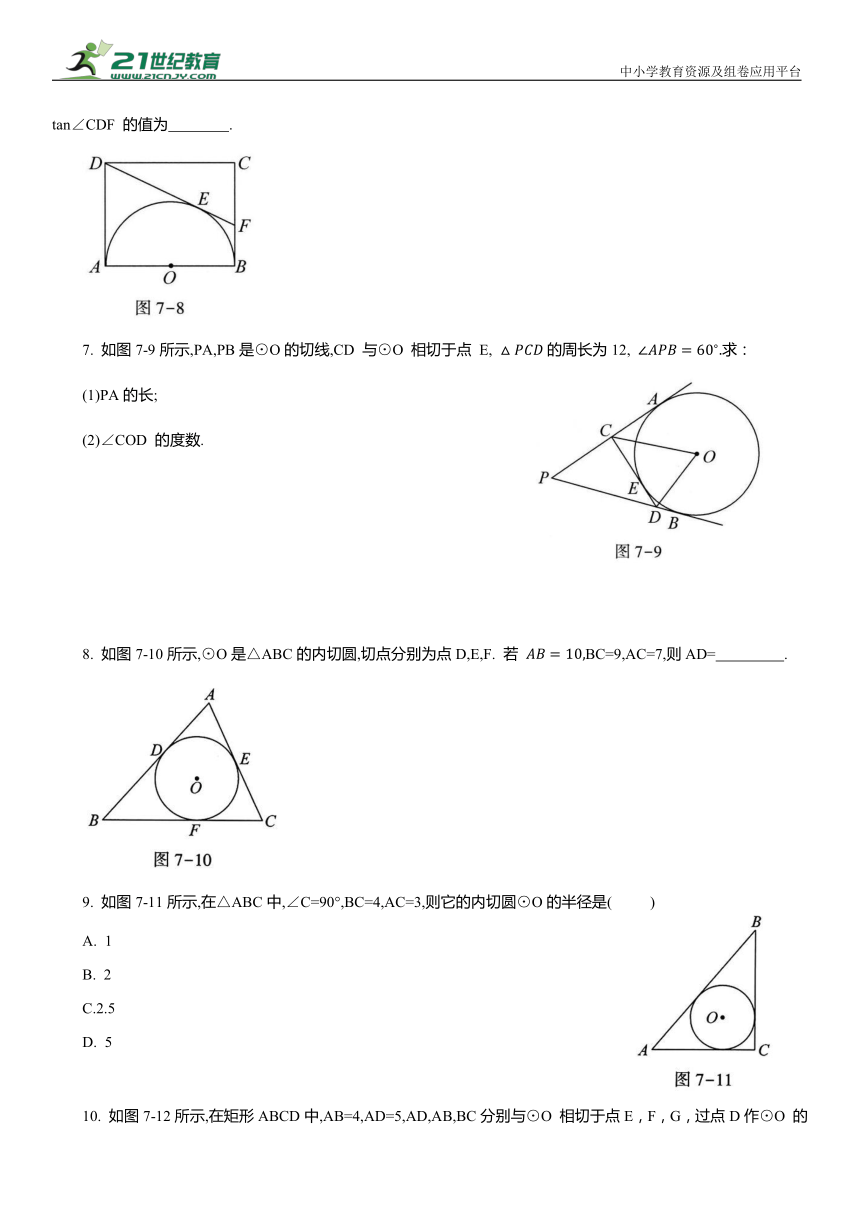
6. 如图7-8所示,在矩形ABCD中, ,以AB 为直径在矩形内作半圆,DE与⊙O 相切于点 E,则tan∠CDF 的值为 .
7. 如图7-9所示,PA,PB是⊙O的切线,CD 与⊙O 相切于点 E, 的周长为12, 求:
(1)PA的长;
(2)∠COD 的度数.
8. 如图7-10所示,⊙O是△ABC的内切圆,切点分别为点D,E,F. 若 BC=9,AC=7,则AD= .
9. 如图7-11所示,在△ABC中,∠C=90°,BC=4,AC=3,则它的内切圆⊙O的半径是( )
A. 1
B. 2
C.2.5
D. 5
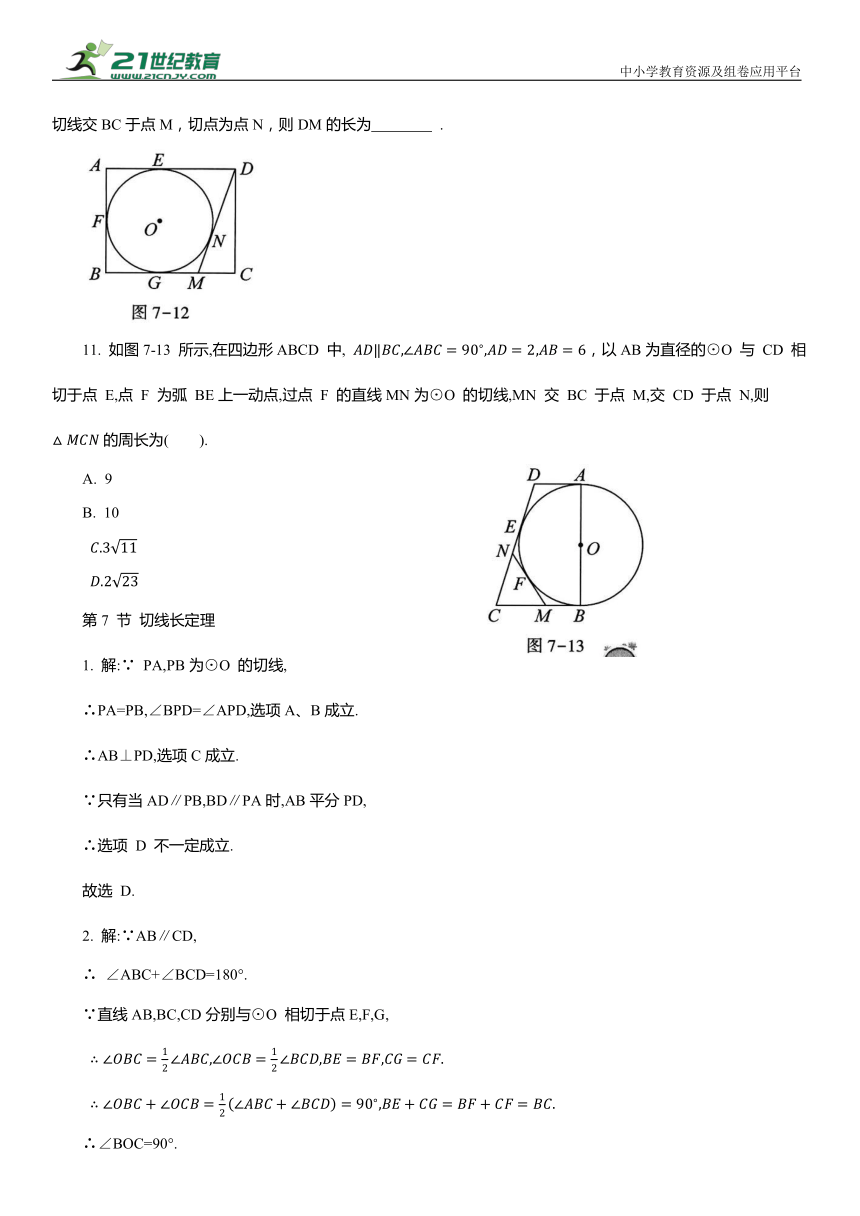
10. 如图7-12所示,在矩形ABCD中,AB=4,AD=5,AD,AB,BC分别与⊙O 相切于点E,F,G,过点D作⊙O 的切线交BC于点M,切点为点N,则DM的长为 .
11. 如图7-13 所示,在四边形ABCD 中, ,以AB为直径的⊙O 与 CD 相切于点 E,点 F 为弧 BE上一动点,过点 F 的直线MN为⊙O 的切线,MN 交 BC 于点 M,交 CD 于点 N,则 的周长为( ).
A. 9
B. 10
第7 节 切线长定理
1. 解:∵ PA,PB为⊙O 的切线,
∴PA=PB,∠BPD=∠APD,选项A、B成立.
∴AB⊥PD,选项C成立.
∵只有当AD∥PB,BD∥PA时,AB平分PD,
∴选项 D 不一定成立.
故选 D.
2. 解:∵AB∥CD,
∴ ∠ABC+∠BCD=180°.
∵直线AB,BC,CD分别与⊙O 相切于点E,F,G,
∴∠BOC=90°.
∵在 Rt△BOC中,
∴ BE+CG=10(cm).
3. 解:∵ PA,PB分别切⊙O于点A,B,
∴PB=PA=4.
∵CD切⊙O 于点 E,且分别交PA,PB 于点 C,D,
∴CA=CE,DB=DE.
∴△PCD的周长=PC+PD+CD=PC+PD+CA+DB=PA+PB=8.
故选 C.
4.解:设光盘的圆心为O,光盘与三角尺的交点为C,三角尺与直尺的交点为A,D,连接OC,OB,OA,如图53所示.
∵AC,AB分别为⊙O 的切线,
∴AO为∠CAB 的角平分线,OC⊥AC,OB⊥AB.
∵∠CAD=60°,
∵在 Rt△AOB中,AB=6cm,
即 解得
∴光盘的直径为
5. 解:∵在 Rt△BCM中,
∵AB为⊙O的直径,且AB⊥BC,
∴BC为⊙O的切线.
∵CD也为⊙O的切线,
∴CD=BC=2.
故选C.
6. 解:∵四边形ABCD 为矩形,
∴∠A=∠B=∠C=90°,CD=AB=4,BC=AD=3.
∵AB为⊙O的直径,
∴AD,BC与半圆相切.
∵DE与⊙O 相切于点 E,
∴DE=DA=3,EF=BF.
设CF=x,则EF=BF=3-x,DF=DE+EF=6-x.
∵在 Rt△DCF中, 即 解得
7. 解:(1)∵PA,PB是⊙O 的切线,CD与⊙O 相切于点 E,
∴CA=CE,DE=DB,PA=PB.
∴△PCD的周长=PD+CD+PC=PD+BD+CA+PC=PB+PA=2PA=12,即PA=6.
(2)∵∠P=60°,
∴∠PCE+∠PDE=120°.
∵ PA,PB是⊙O 的切线,CD与⊙O 相切于点 E,
8. 解:∵⊙O是△ABC的内切圆,切点分别为点 D,E,F,
∴AD=AE,BD=BF,CE=CF.
设AD=AE=x,BD=BF=y,CE=CF=z,
则有 解得x=4.
故AD=4.
9. 解:∵∠C=90°,BC=4,AC=3,
∵⊙O 是△ABC的外接圆,
即 解得r=1.
故选 A.
10. 解:如图54所示,连接OE,OF,ON,OG.
∵ 四边形ABCD是矩形,
∴∠A=∠B=90°,CD=AB=4.
∵AD,AB,BC分别与⊙O 相切于点 E,F,G,
∴ ∠AEO=∠AFO=∠OFB=∠BGO=90°.
∴四边形AFOE,FBGO 是正方形.
∴AF=BF=AE=BG=2.
∴DE=AD-AE=5-2=3.
∵DM是⊙O 的切线,
∴DN=DE=3,MN=MG.
∴ CM=BC-BG-MG=5-2-MN=3-MN.
∵在 Rt△DMC中,
即 解得
11. 解:作DH⊥BC于点 H,如图55所示.
∵在四边形ABCD中,AD∥BC,∠ABC=90°,
∴AB⊥AD,AB⊥BC.
∵AB为⊙O 的直径,
∴AD 和BC为⊙O 的切线.
∵CD 和MN为⊙O的切线,
∴ED=AD=2,CE=CB,NE=NF,MB=MF.
∵DH⊥BC,
∴四边形ABHD为矩形.
∴BH=AD=2,DH=AB=6.
设CB=x,则CH=x-2,CD=x+2.
∵在 Rt△DCH中,( 即 解得
∴△MCN的周长=CN+CM+MN=CN+NE+CM+MB=CE+CB=9.
故选 A.
第 7 节 切线长定理
一、知识梳理
切线长定理:从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.
如图7-1所示,过⊙O外一点 P 可引两条切线 PA,PB,则PA=PB,PO平分∠APB.
【例1】如图 7-2所示,若△ABC 的三边长分别为AB=9,BC=5,CA=6,△ABC的内切圆⊙O 与AB,BC,AC 相切于点 D,E,F,则AF 的长为( ).
A. 5 B. 10
C. 7.5 D.4
解:设AF=x.
∵根据切线长定理得,AD=AF=x,
BE=BD=9-x,CE=CF=6-x,
∴则有9-x+6-x=5,解得x=5,即AF的长为5.
故选A.
二、分层练习
万丈高楼平地起
1. 如图7-3所示,PA,PB为⊙O 的切线,切点分别为点A,B,PO交AB 于点 C,PO的延长线交⊙O 于点 D,下列结论不一定成立的是( ).
A. PA=PB
B.∠BPD=∠APD
C. AB⊥PD
D. AB平分PD
2. 如图7-4所示,直线AB,BC,CD分别与⊙O 相切于点E,F,G,且 若OB=6cm,OC=8cm,则BE+CG的长为 .
3. 如图7-5所示,点P 为⊙O外一点,PA,PB分别切⊙O于点A,B,CD切⊙O于点E 且分别交PA,PB 于点 C,D. 若PA=4,则△PCD的周长为( ).
A. 5
B. 7
C. 8
D. 10
4.为了测量一个光盘的直径,小明把直尺、光盘和三角尺按图7-6所示放置在桌面上,并量出AB=6cm,则这张光盘的直径是 .
5. 如图7-7所示,在. 中, 点A在MB上,以AB为直径作⊙O,与MC相切于点 D,则CD的长为( ).
C. 2
D. 3
6. 如图7-8所示,在矩形ABCD中, ,以AB 为直径在矩形内作半圆,DE与⊙O 相切于点 E,则tan∠CDF 的值为 .
7. 如图7-9所示,PA,PB是⊙O的切线,CD 与⊙O 相切于点 E, 的周长为12, 求:
(1)PA的长;
(2)∠COD 的度数.
8. 如图7-10所示,⊙O是△ABC的内切圆,切点分别为点D,E,F. 若 BC=9,AC=7,则AD= .
9. 如图7-11所示,在△ABC中,∠C=90°,BC=4,AC=3,则它的内切圆⊙O的半径是( )
A. 1
B. 2
C.2.5
D. 5
10. 如图7-12所示,在矩形ABCD中,AB=4,AD=5,AD,AB,BC分别与⊙O 相切于点E,F,G,过点D作⊙O 的切线交BC于点M,切点为点N,则DM的长为 .
11. 如图7-13 所示,在四边形ABCD 中, ,以AB为直径的⊙O 与 CD 相切于点 E,点 F 为弧 BE上一动点,过点 F 的直线MN为⊙O 的切线,MN 交 BC 于点 M,交 CD 于点 N,则 的周长为( ).
A. 9
B. 10
第7 节 切线长定理
1. 解:∵ PA,PB为⊙O 的切线,
∴PA=PB,∠BPD=∠APD,选项A、B成立.
∴AB⊥PD,选项C成立.
∵只有当AD∥PB,BD∥PA时,AB平分PD,
∴选项 D 不一定成立.
故选 D.
2. 解:∵AB∥CD,
∴ ∠ABC+∠BCD=180°.
∵直线AB,BC,CD分别与⊙O 相切于点E,F,G,
∴∠BOC=90°.
∵在 Rt△BOC中,
∴ BE+CG=10(cm).
3. 解:∵ PA,PB分别切⊙O于点A,B,
∴PB=PA=4.
∵CD切⊙O 于点 E,且分别交PA,PB 于点 C,D,
∴CA=CE,DB=DE.
∴△PCD的周长=PC+PD+CD=PC+PD+CA+DB=PA+PB=8.
故选 C.
4.解:设光盘的圆心为O,光盘与三角尺的交点为C,三角尺与直尺的交点为A,D,连接OC,OB,OA,如图53所示.
∵AC,AB分别为⊙O 的切线,
∴AO为∠CAB 的角平分线,OC⊥AC,OB⊥AB.
∵∠CAD=60°,
∵在 Rt△AOB中,AB=6cm,
即 解得
∴光盘的直径为
5. 解:∵在 Rt△BCM中,
∵AB为⊙O的直径,且AB⊥BC,
∴BC为⊙O的切线.
∵CD也为⊙O的切线,
∴CD=BC=2.
故选C.
6. 解:∵四边形ABCD 为矩形,
∴∠A=∠B=∠C=90°,CD=AB=4,BC=AD=3.
∵AB为⊙O的直径,
∴AD,BC与半圆相切.
∵DE与⊙O 相切于点 E,
∴DE=DA=3,EF=BF.
设CF=x,则EF=BF=3-x,DF=DE+EF=6-x.
∵在 Rt△DCF中, 即 解得
7. 解:(1)∵PA,PB是⊙O 的切线,CD与⊙O 相切于点 E,
∴CA=CE,DE=DB,PA=PB.
∴△PCD的周长=PD+CD+PC=PD+BD+CA+PC=PB+PA=2PA=12,即PA=6.
(2)∵∠P=60°,
∴∠PCE+∠PDE=120°.
∵ PA,PB是⊙O 的切线,CD与⊙O 相切于点 E,
8. 解:∵⊙O是△ABC的内切圆,切点分别为点 D,E,F,
∴AD=AE,BD=BF,CE=CF.
设AD=AE=x,BD=BF=y,CE=CF=z,
则有 解得x=4.
故AD=4.
9. 解:∵∠C=90°,BC=4,AC=3,
∵⊙O 是△ABC的外接圆,
即 解得r=1.
故选 A.
10. 解:如图54所示,连接OE,OF,ON,OG.
∵ 四边形ABCD是矩形,
∴∠A=∠B=90°,CD=AB=4.
∵AD,AB,BC分别与⊙O 相切于点 E,F,G,
∴ ∠AEO=∠AFO=∠OFB=∠BGO=90°.
∴四边形AFOE,FBGO 是正方形.
∴AF=BF=AE=BG=2.
∴DE=AD-AE=5-2=3.
∵DM是⊙O 的切线,
∴DN=DE=3,MN=MG.
∴ CM=BC-BG-MG=5-2-MN=3-MN.
∵在 Rt△DMC中,
即 解得
11. 解:作DH⊥BC于点 H,如图55所示.
∵在四边形ABCD中,AD∥BC,∠ABC=90°,
∴AB⊥AD,AB⊥BC.
∵AB为⊙O 的直径,
∴AD 和BC为⊙O 的切线.
∵CD 和MN为⊙O的切线,
∴ED=AD=2,CE=CB,NE=NF,MB=MF.
∵DH⊥BC,
∴四边形ABHD为矩形.
∴BH=AD=2,DH=AB=6.
设CB=x,则CH=x-2,CD=x+2.
∵在 Rt△DCH中,( 即 解得
∴△MCN的周长=CN+CM+MN=CN+NE+CM+MB=CE+CB=9.
故选 A.
同课章节目录
