2025年中考数学几何解题方法复习-- 第8节 圆幂定理(含解析)
文档属性
| 名称 | 2025年中考数学几何解题方法复习-- 第8节 圆幂定理(含解析) | 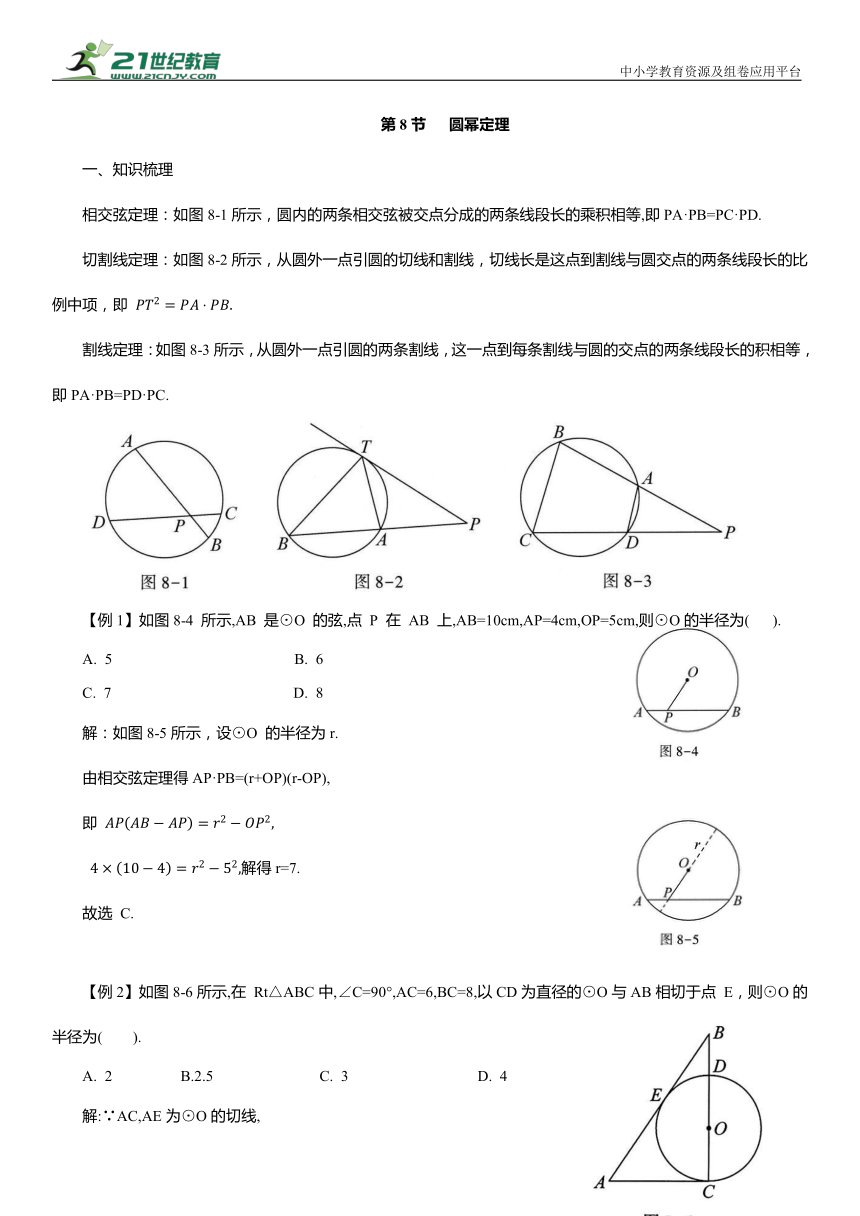 | |
| 格式 | docx | ||
| 文件大小 | 393.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 21:56:01 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第8节 圆幂定理
一、知识梳理
相交弦定理:如图8-1所示,圆内的两条相交弦被交点分成的两条线段长的乘积相等,即PA·PB=PC·PD.
切割线定理:如图8-2所示,从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项,即
割线定理:如图8-3所示,从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等,即PA·PB=PD·PC.
【例1】如图8-4 所示,AB 是⊙O 的弦,点 P 在 AB 上,AB=10cm,AP=4cm,OP=5cm,则⊙O的半径为( ).
A. 5 B. 6
C. 7 D. 8
解:如图8-5所示,设⊙O 的半径为r.
由相交弦定理得AP·PB=(r+OP)(r-OP),
即
解得r=7.
故选 C.
【例2】如图8-6所示,在 Rt△ABC中,∠C=90°,AC=6,BC=8,以CD为直径的⊙O与AB相切于点 E,则⊙O的半径为( ).
A. 2 B.2.5 C. 3 D. 4
解:∵AC,AE为⊙O的切线,
∴AE=AC=6.
∵BC=8,
∴根据勾股定理得AB=10.
∴BE=AB-AE=4.
∵根据切割线定理得
即 解得BD=2,
∴CD=BC-BD=6.
∴ ⊙O 的半径为3.
故选 C.
【例3】如图8-7 所示,⊙O 的割线 PAB 交⊙O 于点A,B,PA=14cm,AB=10cm,PO=20cm,则⊙O的半径为( ).
A.8cm B.10cm C.12cm D.14cm
解:设⊙O的半径为x.
根据割线定理得PA·PB=(PO-r)(PO+r),即 14×(14+10)=(20-x)(20+x),解得x=8.故选 A.
二、分层练习
1. 如图8-8所示,⊙O的弦AB,CD相交于点 P. 若AP=6,BP=8,CP=4,则CD的长为( ).
A. 16
B. 24
C. 12
D.不能确定
2.如图8-9所示,点 P 是直径AB上的一点,且 ,CD 为经过点 P的弦,则 PC 与 PD 的长可能为( ).
A. PC=1,PD=12
B. PC=3,PD=4
C. PC=3,PD=5
D. PC=8,PD=1.5
3. 如图8-10所示,⊙O 的弦AB,CD 相交于点 F, 若 1:4,则CF的长为( ).
A.
B. 2
C. 3
4. 如图8-11 所示,弦BC经过⊙O 的半径 OA的中点 P,且. ,则⊙O的直径为( ).
A. 7
B. 8
C. 9
D. 10
5.如图8-12所示,点P 为弦AB 上的一点,连接OP,过点 P 作. PC交⊙O于点 C,且⊙O的半径为3. 若AP=4,PB=1,则OP的长为( ).
A. 2
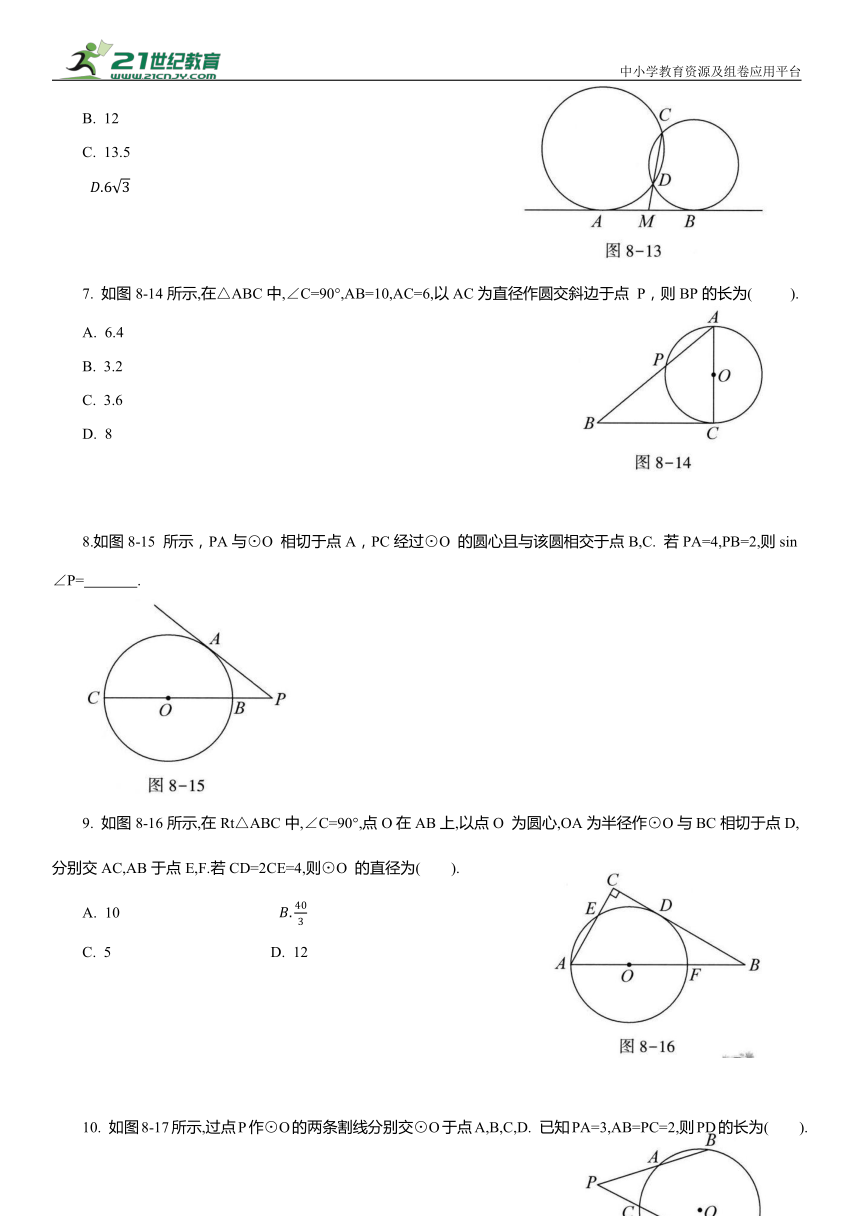
6.如图8-13所示,两圆相交于点 C,D,直线AB与两圆均相切,切点为点A,B,CD的延长线交AB 于点 M. 若CD=9,MD=3,则AB的长为( ).
A. 18
B. 12
C. 13.5
7. 如图8-14所示,在△ABC中,∠C=90°,AB=10,AC=6,以AC为直径作圆交斜边于点 P,则BP的长为( ).
A. 6.4
B. 3.2
C. 3.6
D. 8
8.如图8-15 所示,PA与⊙O 相切于点A,PC经过⊙O 的圆心且与该圆相交于点B,C. 若PA=4,PB=2,则sin∠P= .
9. 如图8-16所示,在Rt△ABC中,∠C=90°,点O在AB上,以点O 为圆心,OA为半径作⊙O与BC相切于点D,分别交AC,AB于点E,F.若CD=2CE=4,则⊙O 的直径为( ).
A. 10
C. 5 D. 12
10. 如图8-17所示,过点P作⊙O的两条割线分别交⊙O于点A,B,C,D. 已知PA=3,AB=PC=2,则PD的长为( ).
A. 3
B. 7.5
C. 5
D. 5.5
11. 如图8-18所示,AB是⊙O 的直径,弦CD⊥AB 于点 E,点 P 是BA 延长线上的一点,连接PC交⊙O 于点 F. 若PF=7,FC=13,PA:AE:EB=2:4:1,则CD的长为 .
12. 如图8-19所示,点P是⊙O 外一点,PAB为⊙O的一条割线,且PA=AB,PO交⊙O 于点 C. 若OC=3,OP=5,则AB的长为( ).
13. 如图8-20 所示,AB 为圆的直径 . 若 AB=AC=5,BD=4,则 的值为( ).
A.
第8节 圆幂定理
1. 解:∵AP·BP=CP·DP,AP=6,BP=8,CP=4,
∴CD=CP+DP=12+4=16.
故选 A.
2. 解:∵PA=2,PB=6,
∴AB=2+6=8,即⊙O 的直径为8.
∵CD是⊙O 的弦,
∴CD≤AB.
A选项中,CD=PC+PD=13,故错误.
B选项中,符合CD≤AB,且PD·PC=PA·PB,故正确.
C选项中,PA·PB≠PC·PD,故错误.
D 选项中,CD=PD+PC=9.5>AB,故错误.
故选 B.
3. 解:∵CF:DF=1:4,
∴DF=4CF.
∵AB=10,AF=2,
∴BF=AB-AF=10-2=8.
∴由相交弦定理得AF·BF=CF·DF,即2×8=CF·4CF,解得CF=2.
故选 B.
4. 解:如图56所示,延长AO交⊙O于点D,设⊙O的半径是x.
根据相交弦定理得 解得x=4,
故⊙O 的直径为8.
故选 B.
5. 解:如图57所示,延长CP交⊙O 于点 D,连接OC.
∵PC⊥OP,
∴ PC=PD.
∵AP=4,PB=1,
解得PC=2.
∵⊙O 的半径为3,
故选C.
A
B
8. 解:如图58所示,连接OA,设⊙O的半径为r,则OP=OB+BP=r+2.
∵ PA与⊙O 相切于点A,
∴OA⊥AP.
∵根据勾股定理得 即 解得r=3,
9. 解:如图59所示,连接OD,过点O 作OG⊥AC于点 G.
∵∠C=90°,OG⊥AC,BC为⊙O 的切线,
∴四边形ODCG是矩形.
∵ CD 是⊙O 切线,CEA是⊙O 的割线,
∵CD=2CE=4,
∴AC=8.
∴AE=6.
∴OD=CG=GE+CE=5.
∴ ⊙O 的直径为10.
故选 A.
10. 解:∵AB=2,PA=3,
∴PB=5.
∵PA·PB=PC·PD,PC=2,
∴PD=7.5.
故选 B.
11. 解:设BE为x,则.PA=2x,PB=7x.
∵根据切割线定理得PA·PB=PF·PC,即2x·7x=7×20,解得
∴CE·DE=AE·BE=4x =40.
∵CD⊥AB 于点 E,
12. 解:如图60所示,延长PO交⊙O 于点 D,设PA=AB=x.
∵PA·PB=PC·PD,OC=3,OP=5,
∴x·2x=16,解得
故选B.
13. 解:连接AD,如图61所示.
∵AB为⊙O的直径,
∴∠E=90°,AD⊥BC.
∵AB=AC=5,BD=4,
∴AD=3,DC=BD=4.
∴BC=2BD=8.
∵∠C=∠C,∠CDA=∠CEB,
∴△CDA∽△CEB.
即 解得
故选 C.
第8节 圆幂定理
一、知识梳理
相交弦定理:如图8-1所示,圆内的两条相交弦被交点分成的两条线段长的乘积相等,即PA·PB=PC·PD.
切割线定理:如图8-2所示,从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项,即
割线定理:如图8-3所示,从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等,即PA·PB=PD·PC.
【例1】如图8-4 所示,AB 是⊙O 的弦,点 P 在 AB 上,AB=10cm,AP=4cm,OP=5cm,则⊙O的半径为( ).
A. 5 B. 6
C. 7 D. 8
解:如图8-5所示,设⊙O 的半径为r.
由相交弦定理得AP·PB=(r+OP)(r-OP),
即
解得r=7.
故选 C.
【例2】如图8-6所示,在 Rt△ABC中,∠C=90°,AC=6,BC=8,以CD为直径的⊙O与AB相切于点 E,则⊙O的半径为( ).
A. 2 B.2.5 C. 3 D. 4
解:∵AC,AE为⊙O的切线,
∴AE=AC=6.
∵BC=8,
∴根据勾股定理得AB=10.
∴BE=AB-AE=4.
∵根据切割线定理得
即 解得BD=2,
∴CD=BC-BD=6.
∴ ⊙O 的半径为3.
故选 C.
【例3】如图8-7 所示,⊙O 的割线 PAB 交⊙O 于点A,B,PA=14cm,AB=10cm,PO=20cm,则⊙O的半径为( ).
A.8cm B.10cm C.12cm D.14cm
解:设⊙O的半径为x.
根据割线定理得PA·PB=(PO-r)(PO+r),即 14×(14+10)=(20-x)(20+x),解得x=8.故选 A.
二、分层练习
1. 如图8-8所示,⊙O的弦AB,CD相交于点 P. 若AP=6,BP=8,CP=4,则CD的长为( ).
A. 16
B. 24
C. 12
D.不能确定
2.如图8-9所示,点 P 是直径AB上的一点,且 ,CD 为经过点 P的弦,则 PC 与 PD 的长可能为( ).
A. PC=1,PD=12
B. PC=3,PD=4
C. PC=3,PD=5
D. PC=8,PD=1.5
3. 如图8-10所示,⊙O 的弦AB,CD 相交于点 F, 若 1:4,则CF的长为( ).
A.
B. 2
C. 3
4. 如图8-11 所示,弦BC经过⊙O 的半径 OA的中点 P,且. ,则⊙O的直径为( ).
A. 7
B. 8
C. 9
D. 10
5.如图8-12所示,点P 为弦AB 上的一点,连接OP,过点 P 作. PC交⊙O于点 C,且⊙O的半径为3. 若AP=4,PB=1,则OP的长为( ).
A. 2
6.如图8-13所示,两圆相交于点 C,D,直线AB与两圆均相切,切点为点A,B,CD的延长线交AB 于点 M. 若CD=9,MD=3,则AB的长为( ).
A. 18
B. 12
C. 13.5
7. 如图8-14所示,在△ABC中,∠C=90°,AB=10,AC=6,以AC为直径作圆交斜边于点 P,则BP的长为( ).
A. 6.4
B. 3.2
C. 3.6
D. 8
8.如图8-15 所示,PA与⊙O 相切于点A,PC经过⊙O 的圆心且与该圆相交于点B,C. 若PA=4,PB=2,则sin∠P= .
9. 如图8-16所示,在Rt△ABC中,∠C=90°,点O在AB上,以点O 为圆心,OA为半径作⊙O与BC相切于点D,分别交AC,AB于点E,F.若CD=2CE=4,则⊙O 的直径为( ).
A. 10
C. 5 D. 12
10. 如图8-17所示,过点P作⊙O的两条割线分别交⊙O于点A,B,C,D. 已知PA=3,AB=PC=2,则PD的长为( ).
A. 3
B. 7.5
C. 5
D. 5.5
11. 如图8-18所示,AB是⊙O 的直径,弦CD⊥AB 于点 E,点 P 是BA 延长线上的一点,连接PC交⊙O 于点 F. 若PF=7,FC=13,PA:AE:EB=2:4:1,则CD的长为 .
12. 如图8-19所示,点P是⊙O 外一点,PAB为⊙O的一条割线,且PA=AB,PO交⊙O 于点 C. 若OC=3,OP=5,则AB的长为( ).
13. 如图8-20 所示,AB 为圆的直径 . 若 AB=AC=5,BD=4,则 的值为( ).
A.
第8节 圆幂定理
1. 解:∵AP·BP=CP·DP,AP=6,BP=8,CP=4,
∴CD=CP+DP=12+4=16.
故选 A.
2. 解:∵PA=2,PB=6,
∴AB=2+6=8,即⊙O 的直径为8.
∵CD是⊙O 的弦,
∴CD≤AB.
A选项中,CD=PC+PD=13,故错误.
B选项中,符合CD≤AB,且PD·PC=PA·PB,故正确.
C选项中,PA·PB≠PC·PD,故错误.
D 选项中,CD=PD+PC=9.5>AB,故错误.
故选 B.
3. 解:∵CF:DF=1:4,
∴DF=4CF.
∵AB=10,AF=2,
∴BF=AB-AF=10-2=8.
∴由相交弦定理得AF·BF=CF·DF,即2×8=CF·4CF,解得CF=2.
故选 B.
4. 解:如图56所示,延长AO交⊙O于点D,设⊙O的半径是x.
根据相交弦定理得 解得x=4,
故⊙O 的直径为8.
故选 B.
5. 解:如图57所示,延长CP交⊙O 于点 D,连接OC.
∵PC⊥OP,
∴ PC=PD.
∵AP=4,PB=1,
解得PC=2.
∵⊙O 的半径为3,
故选C.
A
B
8. 解:如图58所示,连接OA,设⊙O的半径为r,则OP=OB+BP=r+2.
∵ PA与⊙O 相切于点A,
∴OA⊥AP.
∵根据勾股定理得 即 解得r=3,
9. 解:如图59所示,连接OD,过点O 作OG⊥AC于点 G.
∵∠C=90°,OG⊥AC,BC为⊙O 的切线,
∴四边形ODCG是矩形.
∵ CD 是⊙O 切线,CEA是⊙O 的割线,
∵CD=2CE=4,
∴AC=8.
∴AE=6.
∴OD=CG=GE+CE=5.
∴ ⊙O 的直径为10.
故选 A.
10. 解:∵AB=2,PA=3,
∴PB=5.
∵PA·PB=PC·PD,PC=2,
∴PD=7.5.
故选 B.
11. 解:设BE为x,则.PA=2x,PB=7x.
∵根据切割线定理得PA·PB=PF·PC,即2x·7x=7×20,解得
∴CE·DE=AE·BE=4x =40.
∵CD⊥AB 于点 E,
12. 解:如图60所示,延长PO交⊙O 于点 D,设PA=AB=x.
∵PA·PB=PC·PD,OC=3,OP=5,
∴x·2x=16,解得
故选B.
13. 解:连接AD,如图61所示.
∵AB为⊙O的直径,
∴∠E=90°,AD⊥BC.
∵AB=AC=5,BD=4,
∴AD=3,DC=BD=4.
∴BC=2BD=8.
∵∠C=∠C,∠CDA=∠CEB,
∴△CDA∽△CEB.
即 解得
故选 C.
同课章节目录
