2025年中考数学几何解题方法复习-- 第9节 圆中的计算(1)(含解析)
文档属性
| 名称 | 2025年中考数学几何解题方法复习-- 第9节 圆中的计算(1)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 482.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-02 06:16:46 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第9节 圆中的计算(1)
一、知识梳理
【例】如图9-1所示,直线MN交⊙O 于点A,B,AC是直径,AD 平分∠CAM交⊙O 于点 D,过点 D 作 DE⊥MN于点 E.
C
(1)求证:DE是⊙O的切线;
(2)若DE=4cm,AE=3cm,求⊙O的半径.
(1)证明:连接OD,如图9-2所示.
∵OA=OD,
∴∠1=∠2.
∵AD 平分∠CAM,
∴∠2=∠3.
∴∠1=∠3.
∴MN∥OD.
∵DE⊥MN,
∴DE⊥OD.
∴ DE 是⊙O 的切线.
(2)解:连接CD,如图9-3所示.
∵AC是⊙O的直径,
∴∠ADC=90°.
∵DE⊥MN,DE=4cm,AE=3cm,
∴∠AED=90°,
∴∠ADC=∠AED.
又∵∠2=∠3,
∴ △ADC∽△AED.
即 解得
即⊙O的半径为
二、分层练习
万丈高楼平地起
1. 如图9-4所示,AB 是⊙O 的直径,点C在⊙O上,AD 和过点 C的切线CD互相垂直,垂足为点 D.
(1)求证:∠CAD=∠CAB;
(2)若AC=8,OA=5,求CD的长.
2. 如图9-5所示,. 的边AB是⊙O的直径,边AC交⊙O于点 D,边BC与⊙O 相切于点B,点E在⊙O上,连接BD,BE,DE.
(1)求证:
(2)已知 求⊙O的半径.
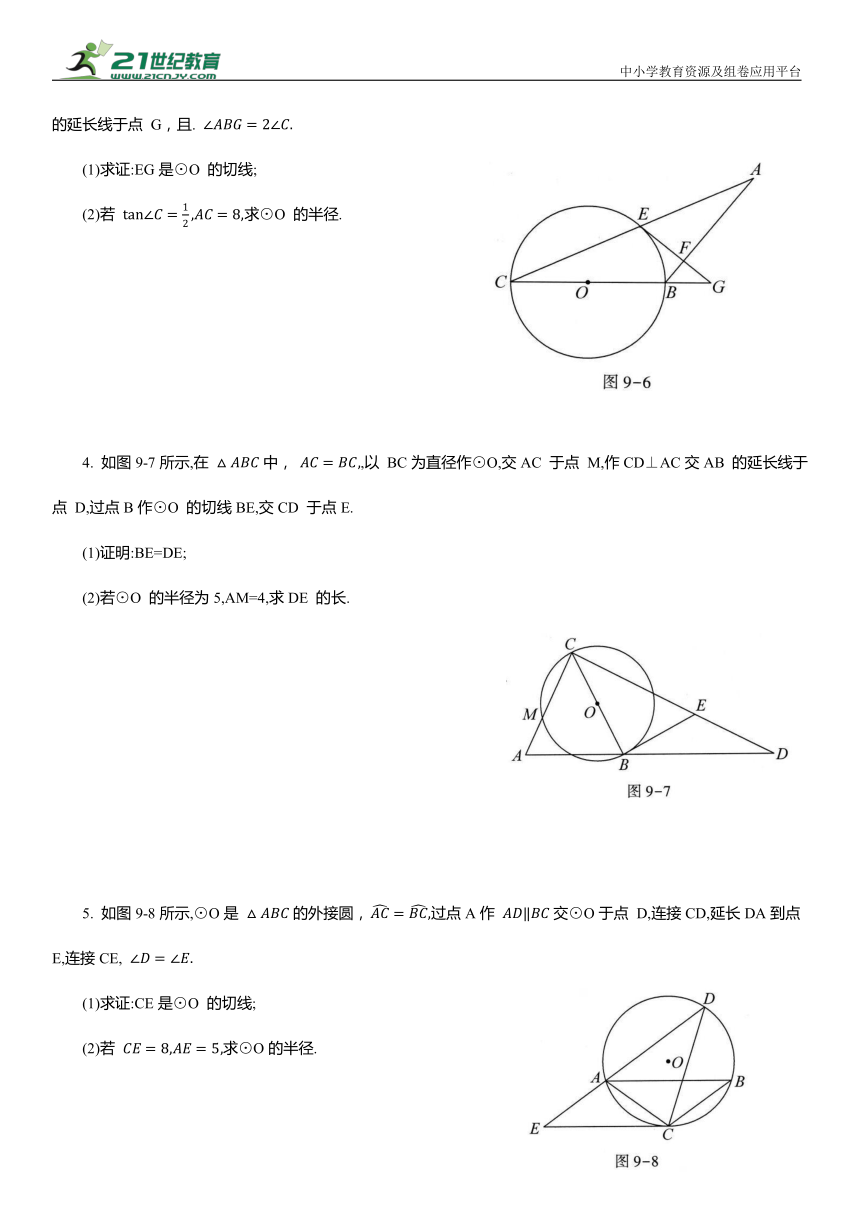
3. 如图9-6所示,在 中,以BC为直径的⊙O交AC于点 E,过点 E 作 AB的垂线交AB 于点 F,交 CB的延长线于点 G,且.
(1)求证:EG是⊙O 的切线;
(2)若 求⊙O 的半径.
4. 如图9-7所示,在 中, ,以 BC为直径作⊙O,交AC 于点 M,作CD⊥AC交AB 的延长线于点 D,过点B作⊙O 的切线BE,交CD 于点E.
(1)证明:BE=DE;
(2)若⊙O 的半径为5,AM=4,求DE 的长.
5. 如图9-8所示,⊙O是 的外接圆, 过点A作 交⊙O于点 D,连接CD,延长DA到点 E,连接CE,
(1)求证:CE是⊙O 的切线;
(2)若 求⊙O的半径.
6. 如图9-9所示,AB是⊙O的直径,点C,D在⊙O上,过点C的切线交DA 的延长线于点 E,且 连接CD,BC.
(1)求证:
(2)若 求 EC 的长.
7. 如图9-10所示,AB为⊙O 的直径,AC为⊙O 的弦,过⊙O外的一点 D 作 于点E,交AC于点F,连接DC并延长交AB的延长线于点P,且 作 于点 H.
(1)判断直线DC与⊙O的位置关系,并说明理由;
(2)若 求AC的长.
8. 如图9-11 所示,AB 是⊙O 的直径,弦 于点G,点 F 是CD上的一点,且满足 连接AF并延长,交⊙O 于点E,连接AD,DE.若(
(1)求证:
(2)求 FG的长;
(3)求 tan∠E 的值.
9. 如图9-12所示,点C 在以AB 为直径的⊙O 上, 的角平分线交⊙O于点 D.过点 D 作AB的平行线,交 CA的延长线于点 E.
(1)求证:DE是⊙O的切线;
(2)若 求DE 的长度.
10. 如图9-13所示,⊙O是 的外接圆, ,过点A作 ,交⊙O于点D,交BC于点E,过点B 作⊙O 的切线,交DA的延长线于点 F.
(1)求证:
(2)若⊙O的半径为2,. ,求DE的长.
第9节 圆中的计算(1)
☆万丈高楼平地起
1.(1)证明:如图62所示,连接OC.
∵ CD 是⊙O 的切线,点 C 为切点,
∴∠DCO=90°.
∵AD⊥CD,
∴∠ADC=90°,AD∥OC.
∴ ∠DAC=∠ACO.
∵OA=OC,
∴∠OAC=∠ACO,则∠CAD=∠CAB.
(2)解:如图63所示,连接OC,BC.
∵AB是⊙O 的直径,
∴∠ACB=90°.
∵AC=8,AB=2AO=10,
∵∠ACB=∠ADC,∠CAD=∠CAB,
∴ △ADC∽△ACB.
即 解得CD=4.8.
2.(1)证明:∵AB是⊙O 的直径,
∴∠ADB=90°.
∴ ∠BAD+∠ABD=90°.
∵BC与⊙O 相切于点 B,
∴AB⊥BC,∠ABC=90°.
∴∠CBD+∠ABD=90°.
∴∠CBD=∠BAD.
∴∠BAD=∠E.
∴ ∠CBD=∠E.
解:
∴∠E=30°.
∴∠CBD=∠BAD=∠E=30°.
∵CD=2,
∴⊙O的半径为:
3.(1)证明:如图64 所示,连接OE,BE.
∴∠C=∠A.
∴BC=BA.
∵ BC是⊙O的直径,
∴∠CEB=90°.
∴CE=AE.
∵CO=OB,
∴OE∥AB.
∵GE⊥AB 于点 F,
∴EG⊥OE.
∵OE是⊙O的半径,
∴ EG是⊙O 的切线.
(2)解:∵AC=8,
∴CE=AE=4.
∴BE=2.
,即⊙O的半径为
4.(1)证明:∵CD⊥AC,
∴ ∠A+∠D=90°.
∵BE与⊙O 相切于点 B,
∴CB⊥BE.
∴∠CBA+∠EBD=90°.
∵AC=BC,
∴∠A=∠CBA.
∴∠EBD=∠D.
∴BE=DE.
(2)解:如图65所示,连接MB.
∵ BC是⊙O 的直径,⊙O的半径为5,
∴BM⊥AC,AC=BC=2×5=10.
∵AM=4,
∴MC=AC-AM=10-4=6.
∵AC⊥CD,
∴MB∥DC.
∴ ∠MBC=∠BCE.
∵∠BMC=∠CBE=90°,
∴△BMC∽△CBE.
即 解得
欲穷千里目,更上一层楼
5.(1)证明:连接OC,如图66所示.
∴∠B=∠DAB.
∵∠B=∠D,
∴∠DAB=∠E.
∴点 C为 的中点.
∵OC为⊙O的半径,
∴OC⊥AB.
∴OC⊥EC.
∵OC是⊙O的半径,
∴ CE是⊙O 的切线.
(2)解:连接OC,OB,OC交AB于点F,如图67所示.
∵AD∥BC,由(1)知AB∥EC,
∴四边形ABCE 为平行四边形.
∴BC=AE=5,AB=EC=8.
∵OC⊥AB,
设⊙O半径的长为r,则OF=OC-FC=r-3.
在Rt△OFB中, 即 解得
6.(1)证明:如图68所示,连接OC.
∵ CE 是⊙O 的切线,
∴OC⊥CE.
∵DE⊥CE,
∴OC∥DE.
∴∠DAB=∠AOC.
∵∠AOC=2∠ABC,
∴ ∠DAB=2∠ABC.
(2)解:如图69所示,连接AC.
∵AB是⊙O的直径,
∴ ∠ACB=∠AEC,∠ABC+∠BAC=90°.
∵OC⊥CE,
∴ ∠OCA+∠ACE=90°.
∵OA=OC,
∴ ∠OAC=∠OCA.
∴∠ACE=∠ABC.
∴ △ACE∽△ABC.
即 解得
7. 解:(1)如图70所示,连接OC.
∵∠COB=2∠A,∠D=2∠A,
∴∠COB=∠D.
∵DE⊥AP,
∴∠DEP=90°.
∴∠P+∠D=90°.
∴ ∠P+∠COB=90°.
∴∠OCP=90°.
∴OC⊥DC.
∵OC为⊙O的半径,
∴DC与⊙O 相切.
(2)∵由(1)可知,∠OCP=90°,∠COP=∠D,
∵CH⊥AB,
∴∠CHO=90°.
设⊙O 的半径为r,则OH=r-2.
∵在 Rt△CHO中, 解得r=5.
∴OH=5-2=3.
∴由勾股定理可得CH=4.
∴AH=AB-HB=10-2=8.
∴在 Rt△AHC 中,由勾股定理可得
8. 解:(1)∵AB是⊙O 的直径,弦CD⊥AB,∴DG=CG.
∴由垂径定理可知
∴ ∠ADF=∠AED.
∵ ∠FAD=∠DAE(公共角).
∴ △ADF∽△AED.
∴ FD=6.
∴CD=DF+CF=8,CG=DG=4.
∴FG=CG-CF=2.
(3)∵AF=3,FG=2,
∴在△AFG中,由勾股定理可得
9. 解:(1)如图71 所示,连接OD.
∵AB是⊙O 的直径,CD平分∠ACB,
∴∠ACD=45°.
∴∠AOD=2∠ACD=90°.
∵DE∥AB,
又∵OD为⊙O的半径,
∴DE 是⊙O 的切线.
(2)如图72所示,过点A作AF⊥DE于点F,则四边形AODF是正方形.
∵AB 是⊙O 的直径,
∴ ∠ACB=90°.
∵AC=6,BC=8,
∴AB=10.
∴AF=OD=FD=AO=5.
∴∠EAF=90°-∠CAB=∠ABC.
∴tan∠EAF=tan∠ABC,即
解得
10.(1)证明:∵ BF为⊙O 的切线,
∴FB⊥BD.
∴∠FBD=90°.
∴∠FBA+∠ABD=90°.
∵AD⊥AB,
∴∠BAD=90°.
∴ ∠D+∠ABD=90°.
∴∠FBA=∠D.
∵∠D=∠C,
∴∠FBA=∠C.
∵AB=AC,
∴∠C=∠ABE.
∴∠ABE=∠FBA.
又∵AB=AB,∠BAE=∠BAF=90°,
∴ △BAF≌△BAE(ASA).
∴AF=AE.
(2)解:∵由(1)可知,
△BAF≌△BAE,
∴BF=BE=3.
∵⊙O 的半径为2,
∴BD=4.
即 解得
第9节 圆中的计算(1)
一、知识梳理
【例】如图9-1所示,直线MN交⊙O 于点A,B,AC是直径,AD 平分∠CAM交⊙O 于点 D,过点 D 作 DE⊥MN于点 E.
C
(1)求证:DE是⊙O的切线;
(2)若DE=4cm,AE=3cm,求⊙O的半径.
(1)证明:连接OD,如图9-2所示.
∵OA=OD,
∴∠1=∠2.
∵AD 平分∠CAM,
∴∠2=∠3.
∴∠1=∠3.
∴MN∥OD.
∵DE⊥MN,
∴DE⊥OD.
∴ DE 是⊙O 的切线.
(2)解:连接CD,如图9-3所示.
∵AC是⊙O的直径,
∴∠ADC=90°.
∵DE⊥MN,DE=4cm,AE=3cm,
∴∠AED=90°,
∴∠ADC=∠AED.
又∵∠2=∠3,
∴ △ADC∽△AED.
即 解得
即⊙O的半径为
二、分层练习
万丈高楼平地起
1. 如图9-4所示,AB 是⊙O 的直径,点C在⊙O上,AD 和过点 C的切线CD互相垂直,垂足为点 D.
(1)求证:∠CAD=∠CAB;
(2)若AC=8,OA=5,求CD的长.
2. 如图9-5所示,. 的边AB是⊙O的直径,边AC交⊙O于点 D,边BC与⊙O 相切于点B,点E在⊙O上,连接BD,BE,DE.
(1)求证:
(2)已知 求⊙O的半径.
3. 如图9-6所示,在 中,以BC为直径的⊙O交AC于点 E,过点 E 作 AB的垂线交AB 于点 F,交 CB的延长线于点 G,且.
(1)求证:EG是⊙O 的切线;
(2)若 求⊙O 的半径.
4. 如图9-7所示,在 中, ,以 BC为直径作⊙O,交AC 于点 M,作CD⊥AC交AB 的延长线于点 D,过点B作⊙O 的切线BE,交CD 于点E.
(1)证明:BE=DE;
(2)若⊙O 的半径为5,AM=4,求DE 的长.
5. 如图9-8所示,⊙O是 的外接圆, 过点A作 交⊙O于点 D,连接CD,延长DA到点 E,连接CE,
(1)求证:CE是⊙O 的切线;
(2)若 求⊙O的半径.
6. 如图9-9所示,AB是⊙O的直径,点C,D在⊙O上,过点C的切线交DA 的延长线于点 E,且 连接CD,BC.
(1)求证:
(2)若 求 EC 的长.
7. 如图9-10所示,AB为⊙O 的直径,AC为⊙O 的弦,过⊙O外的一点 D 作 于点E,交AC于点F,连接DC并延长交AB的延长线于点P,且 作 于点 H.
(1)判断直线DC与⊙O的位置关系,并说明理由;
(2)若 求AC的长.
8. 如图9-11 所示,AB 是⊙O 的直径,弦 于点G,点 F 是CD上的一点,且满足 连接AF并延长,交⊙O 于点E,连接AD,DE.若(
(1)求证:
(2)求 FG的长;
(3)求 tan∠E 的值.
9. 如图9-12所示,点C 在以AB 为直径的⊙O 上, 的角平分线交⊙O于点 D.过点 D 作AB的平行线,交 CA的延长线于点 E.
(1)求证:DE是⊙O的切线;
(2)若 求DE 的长度.
10. 如图9-13所示,⊙O是 的外接圆, ,过点A作 ,交⊙O于点D,交BC于点E,过点B 作⊙O 的切线,交DA的延长线于点 F.
(1)求证:
(2)若⊙O的半径为2,. ,求DE的长.
第9节 圆中的计算(1)
☆万丈高楼平地起
1.(1)证明:如图62所示,连接OC.
∵ CD 是⊙O 的切线,点 C 为切点,
∴∠DCO=90°.
∵AD⊥CD,
∴∠ADC=90°,AD∥OC.
∴ ∠DAC=∠ACO.
∵OA=OC,
∴∠OAC=∠ACO,则∠CAD=∠CAB.
(2)解:如图63所示,连接OC,BC.
∵AB是⊙O 的直径,
∴∠ACB=90°.
∵AC=8,AB=2AO=10,
∵∠ACB=∠ADC,∠CAD=∠CAB,
∴ △ADC∽△ACB.
即 解得CD=4.8.
2.(1)证明:∵AB是⊙O 的直径,
∴∠ADB=90°.
∴ ∠BAD+∠ABD=90°.
∵BC与⊙O 相切于点 B,
∴AB⊥BC,∠ABC=90°.
∴∠CBD+∠ABD=90°.
∴∠CBD=∠BAD.
∴∠BAD=∠E.
∴ ∠CBD=∠E.
解:
∴∠E=30°.
∴∠CBD=∠BAD=∠E=30°.
∵CD=2,
∴⊙O的半径为:
3.(1)证明:如图64 所示,连接OE,BE.
∴∠C=∠A.
∴BC=BA.
∵ BC是⊙O的直径,
∴∠CEB=90°.
∴CE=AE.
∵CO=OB,
∴OE∥AB.
∵GE⊥AB 于点 F,
∴EG⊥OE.
∵OE是⊙O的半径,
∴ EG是⊙O 的切线.
(2)解:∵AC=8,
∴CE=AE=4.
∴BE=2.
,即⊙O的半径为
4.(1)证明:∵CD⊥AC,
∴ ∠A+∠D=90°.
∵BE与⊙O 相切于点 B,
∴CB⊥BE.
∴∠CBA+∠EBD=90°.
∵AC=BC,
∴∠A=∠CBA.
∴∠EBD=∠D.
∴BE=DE.
(2)解:如图65所示,连接MB.
∵ BC是⊙O 的直径,⊙O的半径为5,
∴BM⊥AC,AC=BC=2×5=10.
∵AM=4,
∴MC=AC-AM=10-4=6.
∵AC⊥CD,
∴MB∥DC.
∴ ∠MBC=∠BCE.
∵∠BMC=∠CBE=90°,
∴△BMC∽△CBE.
即 解得
欲穷千里目,更上一层楼
5.(1)证明:连接OC,如图66所示.
∴∠B=∠DAB.
∵∠B=∠D,
∴∠DAB=∠E.
∴点 C为 的中点.
∵OC为⊙O的半径,
∴OC⊥AB.
∴OC⊥EC.
∵OC是⊙O的半径,
∴ CE是⊙O 的切线.
(2)解:连接OC,OB,OC交AB于点F,如图67所示.
∵AD∥BC,由(1)知AB∥EC,
∴四边形ABCE 为平行四边形.
∴BC=AE=5,AB=EC=8.
∵OC⊥AB,
设⊙O半径的长为r,则OF=OC-FC=r-3.
在Rt△OFB中, 即 解得
6.(1)证明:如图68所示,连接OC.
∵ CE 是⊙O 的切线,
∴OC⊥CE.
∵DE⊥CE,
∴OC∥DE.
∴∠DAB=∠AOC.
∵∠AOC=2∠ABC,
∴ ∠DAB=2∠ABC.
(2)解:如图69所示,连接AC.
∵AB是⊙O的直径,
∴ ∠ACB=∠AEC,∠ABC+∠BAC=90°.
∵OC⊥CE,
∴ ∠OCA+∠ACE=90°.
∵OA=OC,
∴ ∠OAC=∠OCA.
∴∠ACE=∠ABC.
∴ △ACE∽△ABC.
即 解得
7. 解:(1)如图70所示,连接OC.
∵∠COB=2∠A,∠D=2∠A,
∴∠COB=∠D.
∵DE⊥AP,
∴∠DEP=90°.
∴∠P+∠D=90°.
∴ ∠P+∠COB=90°.
∴∠OCP=90°.
∴OC⊥DC.
∵OC为⊙O的半径,
∴DC与⊙O 相切.
(2)∵由(1)可知,∠OCP=90°,∠COP=∠D,
∵CH⊥AB,
∴∠CHO=90°.
设⊙O 的半径为r,则OH=r-2.
∵在 Rt△CHO中, 解得r=5.
∴OH=5-2=3.
∴由勾股定理可得CH=4.
∴AH=AB-HB=10-2=8.
∴在 Rt△AHC 中,由勾股定理可得
8. 解:(1)∵AB是⊙O 的直径,弦CD⊥AB,∴DG=CG.
∴由垂径定理可知
∴ ∠ADF=∠AED.
∵ ∠FAD=∠DAE(公共角).
∴ △ADF∽△AED.
∴ FD=6.
∴CD=DF+CF=8,CG=DG=4.
∴FG=CG-CF=2.
(3)∵AF=3,FG=2,
∴在△AFG中,由勾股定理可得
9. 解:(1)如图71 所示,连接OD.
∵AB是⊙O 的直径,CD平分∠ACB,
∴∠ACD=45°.
∴∠AOD=2∠ACD=90°.
∵DE∥AB,
又∵OD为⊙O的半径,
∴DE 是⊙O 的切线.
(2)如图72所示,过点A作AF⊥DE于点F,则四边形AODF是正方形.
∵AB 是⊙O 的直径,
∴ ∠ACB=90°.
∵AC=6,BC=8,
∴AB=10.
∴AF=OD=FD=AO=5.
∴∠EAF=90°-∠CAB=∠ABC.
∴tan∠EAF=tan∠ABC,即
解得
10.(1)证明:∵ BF为⊙O 的切线,
∴FB⊥BD.
∴∠FBD=90°.
∴∠FBA+∠ABD=90°.
∵AD⊥AB,
∴∠BAD=90°.
∴ ∠D+∠ABD=90°.
∴∠FBA=∠D.
∵∠D=∠C,
∴∠FBA=∠C.
∵AB=AC,
∴∠C=∠ABE.
∴∠ABE=∠FBA.
又∵AB=AB,∠BAE=∠BAF=90°,
∴ △BAF≌△BAE(ASA).
∴AF=AE.
(2)解:∵由(1)可知,
△BAF≌△BAE,
∴BF=BE=3.
∵⊙O 的半径为2,
∴BD=4.
即 解得
同课章节目录
