2025年中考数学几何解题方法复习-- 第 10节 圆中的计算(2)(含解析)
文档属性
| 名称 | 2025年中考数学几何解题方法复习-- 第 10节 圆中的计算(2)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 415.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 21:41:23 | ||
图片预览

文档简介
第 10节 圆中的计算(2)
一、知识梳理
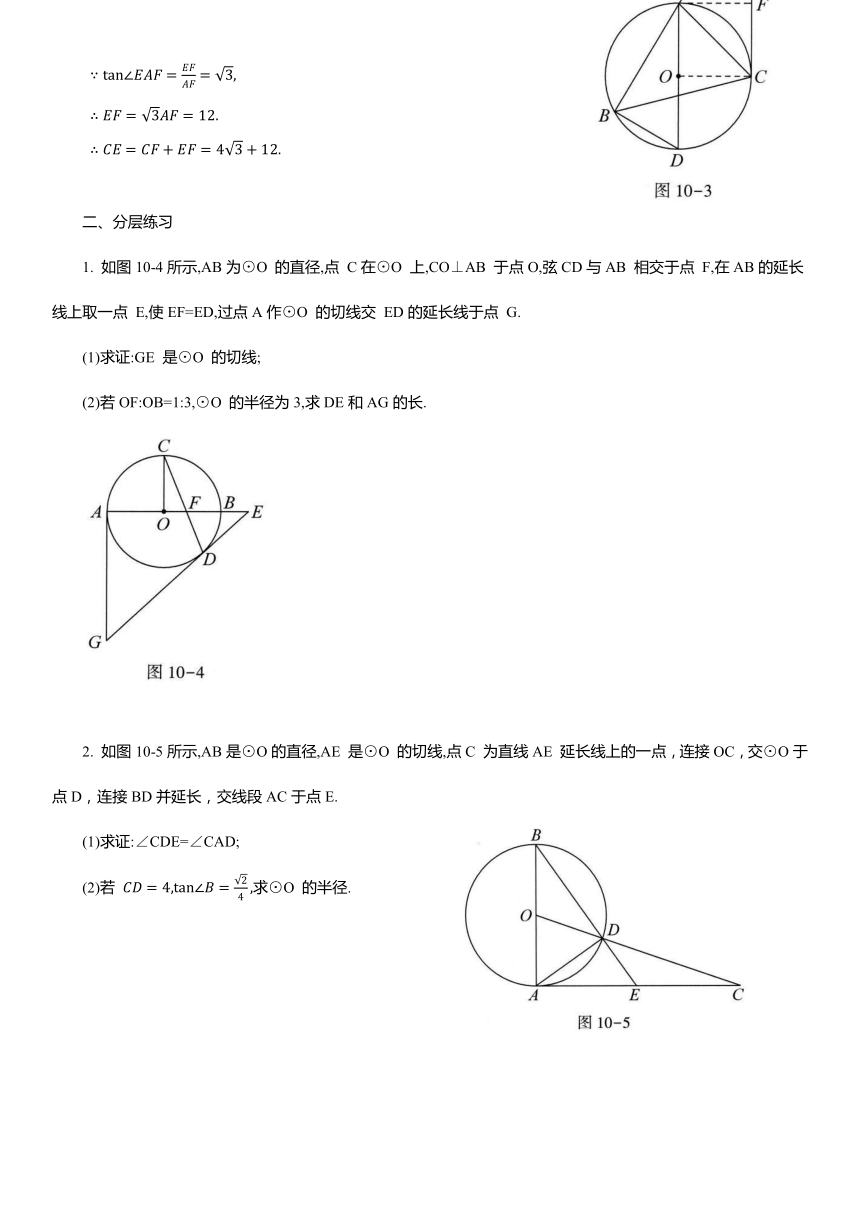
【例】如图10-1所示,△ABC是⊙O 的内接三角形,∠BAC=75°,∠ABC=45°. 连接AO并延长,交⊙O 于点D,连接BD. 过点C作⊙O的切线,交BA的延长线于点 E.
(1)求证:AD∥EC;
(2)若AB=12,求线段EC的长.
证明:(1)如图10-2所示,连接OC.
∵CE与⊙O 相切于点 C,
∴ ∠OCE=90°.
∵∠ABC=45°,
∴∠AOC=90°.
∵∠AOC+∠OCE=180°,
∴AD∥EC.
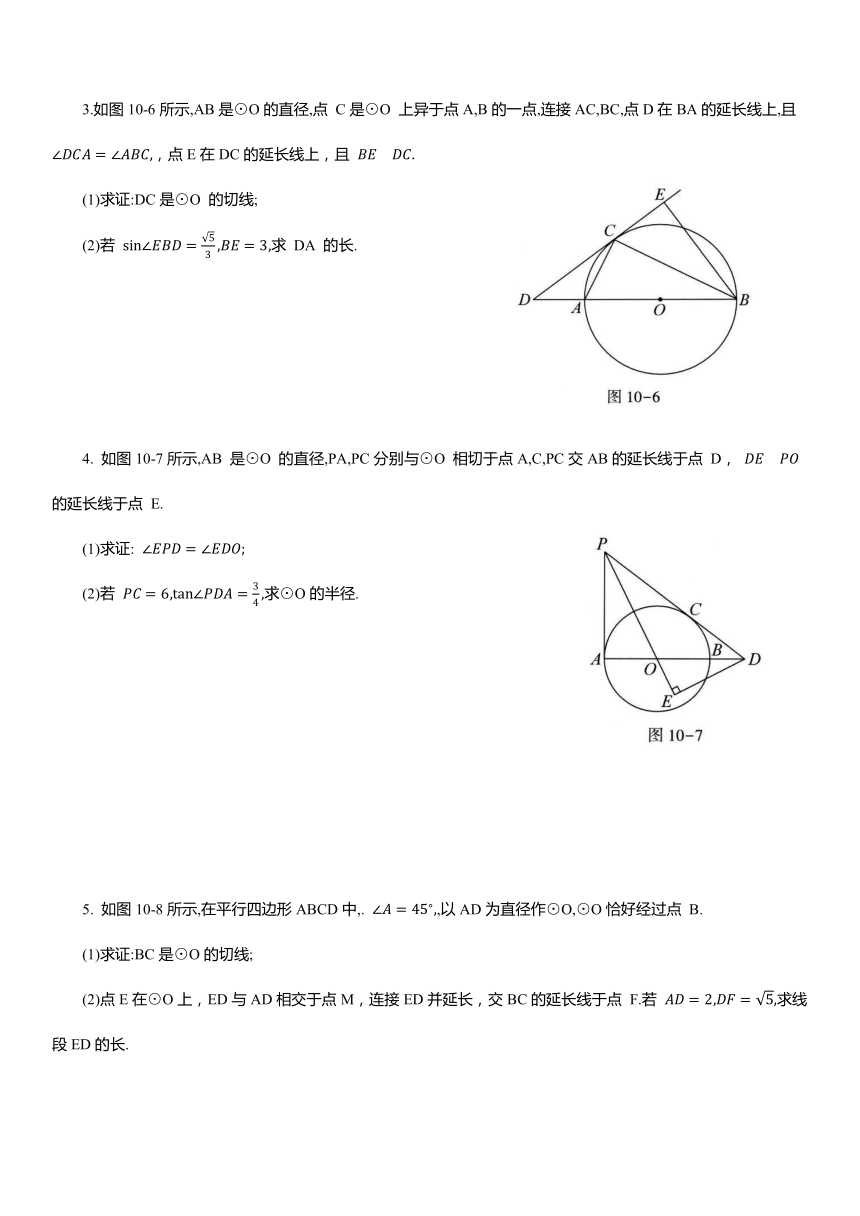
(2)如图10-3所示,过点A 作AF⊥EC交EC于点 F.
∵∠BAC=75°,∠ABC=45°,
∴∠ACB=60°.
∴ ∠D=∠ACB=60°.
∵AD是⊙O的直径,
∴∠ABD=90°.
∵AB=12,
∵AF⊥EC,∠OCE=90°,∠AOC=90°,OA=OC,
∴ 四边形 OAFC 是正方形.
二、分层练习
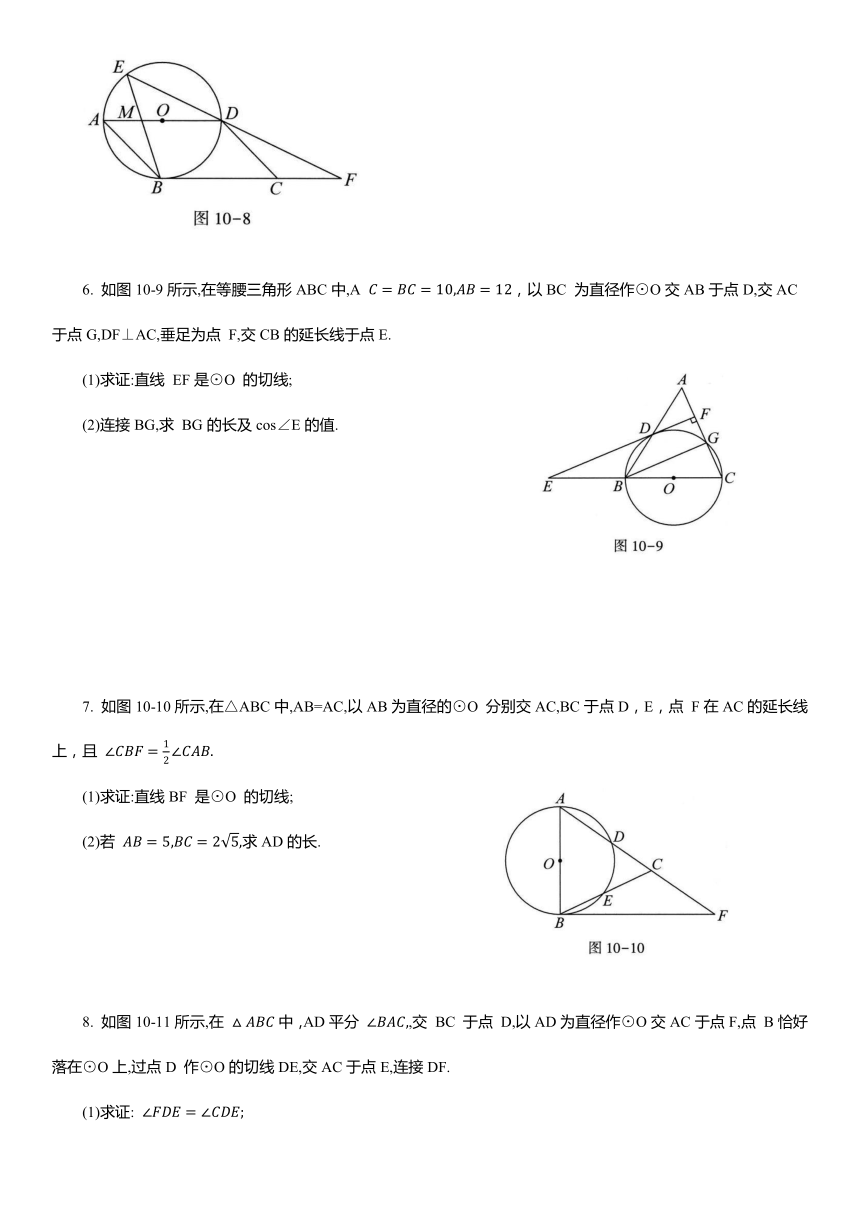
1. 如图10-4所示,AB为⊙O 的直径,点 C在⊙O 上,CO⊥AB 于点O,弦CD与AB 相交于点 F,在AB的延长线上取一点 E,使EF=ED,过点A作⊙O 的切线交 ED的延长线于点 G.
(1)求证:GE 是⊙O 的切线;
(2)若OF:OB=1:3,⊙O 的半径为3,求DE和AG的长.
2. 如图10-5所示,AB是⊙O的直径,AE 是⊙O 的切线,点C 为直线AE 延长线上的一点,连接OC,交⊙O于点D,连接BD并延长,交线段AC于点E.
(1)求证:∠CDE=∠CAD;
(2)若 求⊙O 的半径.
3.如图10-6所示,AB是⊙O的直径,点 C是⊙O 上异于点A,B的一点,连接AC,BC,点D在BA的延长线上,且 ,点E在DC的延长线上,且
(1)求证:DC是⊙O 的切线;
(2)若 求 DA 的长.
4. 如图10-7所示,AB 是⊙O 的直径,PA,PC分别与⊙O 相切于点A,C,PC交AB的延长线于点 D, 的延长线于点 E.
(1)求证:
(2)若 求⊙O的半径.
5. 如图10-8所示,在平行四边形ABCD中,. ,以AD为直径作⊙O,⊙O恰好经过点 B.
(1)求证:BC是⊙O的切线;
(2)点E在⊙O上,ED与AD相交于点M,连接ED并延长,交BC的延长线于点 F.若 求线段ED的长.
6. 如图10-9所示,在等腰三角形ABC中,A ,以BC 为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为点 F,交CB的延长线于点E.
(1)求证:直线 EF是⊙O 的切线;
(2)连接BG,求 BG的长及cos∠E的值.
7. 如图10-10所示,在△ABC中,AB=AC,以AB为直径的⊙O 分别交AC,BC于点D,E,点 F在AC的延长线上,且
(1)求证:直线BF 是⊙O 的切线;
(2)若 求AD的长.
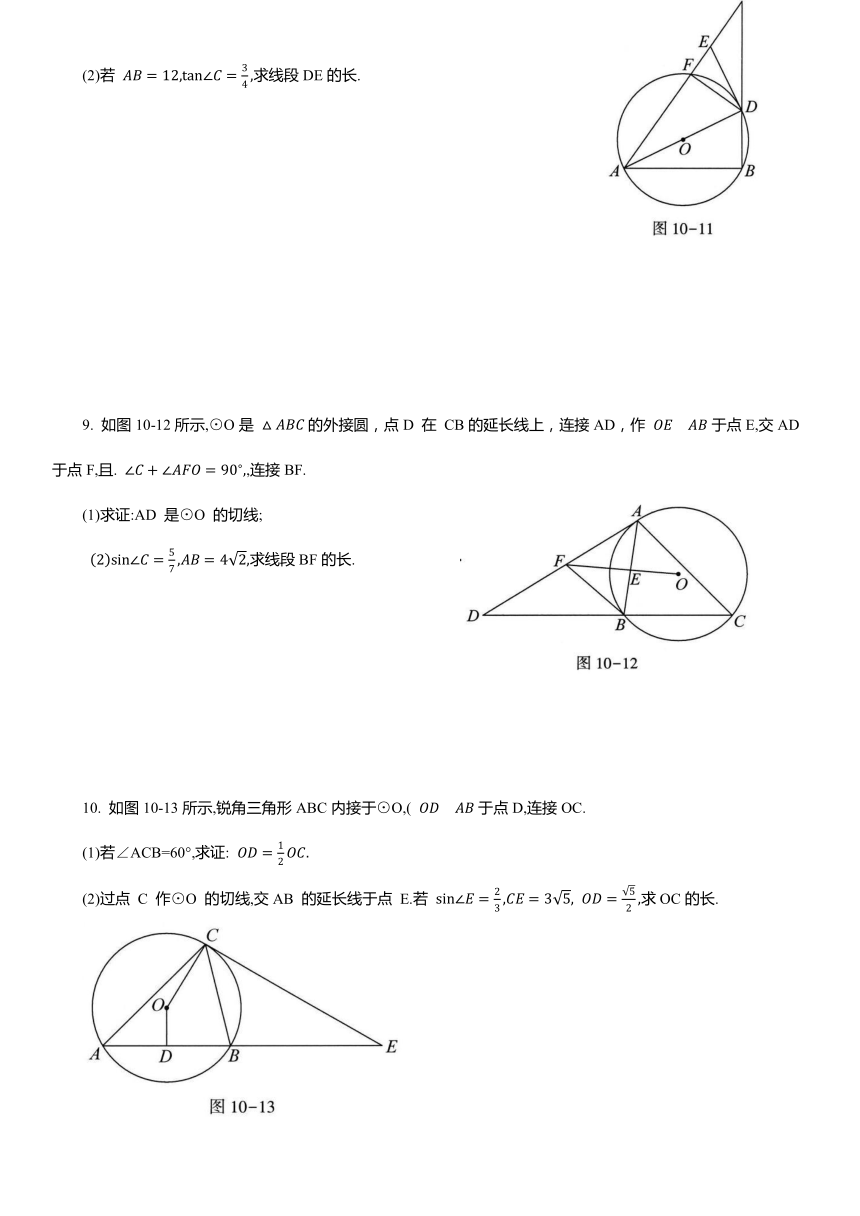
8. 如图10-11所示,在 中,AD平分 ,交 BC 于点 D,以AD为直径作⊙O交AC于点F,点 B恰好落在⊙O上,过点D 作⊙O的切线DE,交AC于点E,连接DF.
(1)求证:
(2)若 求线段DE的长.
9. 如图10-12所示,⊙O是 的外接圆,点D 在 CB的延长线上,连接AD,作 于点E,交AD于点F,且. ,连接BF.
(1)求证:AD 是⊙O 的切线;
求线段BF的长.
10. 如图10-13所示,锐角三角形ABC内接于⊙O,( 于点D,连接OC.
(1)若∠ACB=60°,求证:
(2)过点 C 作⊙O 的切线,交AB 的延长线于点 E.若 求OC的长.
第10节 圆中的计算(2)
1.(1)证明:连接OD,如图73所示.
∵OC=OD,
∴∠C=∠ODC.
∵OC⊥AB,
∴∠COF=90°.
∴∠C+∠CFO=90°.
∴∠ODC+∠CFO=90°.
∵EF=ED,
∴ ∠EFD=∠EDF.
∵∠CFO=∠EFD,
∴∠ODC+∠EDF=90°.
∴∠ODE=90°.
∵OD为⊙O的半径,
∴GE为⊙O的切线.
(2)解:∵OF:OB=1:3,⊙O 的半径为3,
∴OF=1.
设DE=x,则EF=x,OE=1+x.
∵在Rt△ODE中,( 即 解得x=4,
∴DE=4,OE=5.
∵AG为⊙O的切线,
∴AG⊥AE.
∴∠GAE=90°.
又∵∠OED=∠GEA,
∴ Rt△EOD∽Rt△EGA.
即 解得AG=6.
2.(1)证明:∵AE是⊙O 的切线, (2)解:∵∠B=∠DAE,
∴∠OAE=90°.
∴∠OAD+∠CAD=90°.
∵AB是⊙O的直径, ∵∠CDE=∠CAD,∠C=∠C,
∴∠ODB+∠ODA=∠ADB=90°. ∴△CDE∽△CAD.
∴ ∠B+∠OAD=90°.
∵OB=OD, ∵CD=4,
∴∠B=∠ODB.
∵∠ODB=∠CDE, 解得
∴ ∠CDE=∠CAD. 设⊙O 的半径为r.
∴在Rt△OAC中,即 解得r=14.
3.(1)证明:连接OC,如图74所示.
∵AB是⊙O的直径,
∴∠OCD=∠DCA+∠ACO=90°.
∵OC是⊙O的半径,
∴DC是⊙O 的切线.
(2)解:∵BE⊥DC,
∴∠BEC=90°.
∴∠BEC=∠OCD.
∴OC∥BE.
∴∠EBD=∠COD.
∴在 Rt△OCD中,
设
∴OA=OB=OC=2a.
∴DA=OD-OA=3a-2a=a.
∵∠EBD=∠COD,∠BEC=∠OCD,
∴△DEB∽△DCO.
即 解得
4. (1)证明:∵PA,PC分别与⊙O 相切于点A,C,DE⊥PO的延长线于点 E,
∴∠APE=∠EPD,∠PAO=∠DEO=90°.
又∵∠AOP=∠EOD,
∴△PAO∽△DEO.
∴∠APO=∠EDO.
∴∠EPD=∠EDO.
(2)如图75所示,连接OC.
∵ PA,PC分别与⊙O 相切于点A,C,
∴ PA=PC=6,∠PAO=∠PCO=90°.
设OC=3x,DC=4x,则OD=5x,AD=OA+OD=8x,PD=PC+CD=6+4x.
∵在 Rt△PAD中, 即 解得 (舍去),
∴OC=3.
∴⊙O 的半径为3.
5.(1)证明:如图76所示,连接BD,OB.
∵∠A=45°,OA=OB,
∴∠ABO=45°.
∴ ∠AOB=90°.
∵四边形ABCD 是平行四边形,
∴AD∥BC.
∴∠OBC=∠AOB=90°.
∴BC⊥OB,
又∵OB 是⊙O的半径,
∴BC为⊙O的切线.
(2)解:如图77所示,过点 D 作DG⊥BC于点G,则∠DGB=∠DGF=90°,DG∥OB.
∵OB=OD,∠OBG=∠DGF=∠BOD=90°,
∴四边形 BODG是正方形,
∵在Rt△DGF中,
∴由切割线定理可知,
即 解得
6.(1)证明:如图78所示,连接OD,CD.
∵BC是⊙O的直径,
∴CD⊥AB.
∵AC=BC,AB=12,
∴AD=BD=6.
∵点O 为BC的中点,
∴OD∥AC.
∵DF⊥AC,
∴OD⊥EF.
∴EF是⊙O的切线.
(2)解:如图79所示,连接BG.
∵ BC是⊙O 的直径,
∴∠BDC=90°.
∵BG⊥AC,DF⊥AC,
∴BG∥EF.
∴∠E=∠CBG.
7.(1)证明:连接AE,∠1和∠2如图80所示.
∵AB 是⊙O 的直径,
∴∠AEB=90°.
∴ ∠1+∠2=90°.
∵AB=AC,
∴∠1=∠CBF.
∴∠CBF+∠2=90°,即∠ABF=90°.
∵AB 是⊙O的直径,
∴直线 BF是⊙O 的切线.
(2)解:如图81所示,连接BD,过点C作CG⊥AB 于点 G.
∵在 Rt△ABE中,由勾股定理得
∴在 Rt△CBG中,GC=BC·sin∠2=4,GB=BC·cos∠2=2.
∴AG=AB-GB=3.
∵GC∥BF,
∴△AGC∽△ABF.
即
即 解得BD=4.
8.(1)证明:∵DE是⊙O 的切线,AD 是⊙O 的直径,
∴AD⊥DE.
°.
∴∠ADB+∠CDE=90°.
∵AD平分∠BAC,
∴ ∠FAD=∠BAD,
在△FAD 和△BAD中,
∴△FAD≌△BAD(AAS).
∴∠ADF=∠ADB.
∴∠FDE=∠CDE.
(2)解:∵在Rt△ABC中,
∵△FAD≌△BAD,
∴AF=AB=12.
∴CF=AC-AF=20-12=8.
∵在 Rt△CDF中,
∴BD=DF=6.
∴ △EAD∽△DAB.
即 解得AE=15.
9.(1)证明:连接OA,OB,如图82所示.
∵ ∠C+∠AFO=90°,
∴∠OAF=90°.
∴OA⊥AD.
∵OA是⊙O的半径,
∴AD是⊙O的切线.
(2)解:∵由(1)可知,∠AOF=∠C,
∵OE⊥AB,
.
10.(1)证明:如图83所示,连接OA,OB.
∵∠ACB=60°,
∴∠AOB=2∠ACB=120°.
∵OA=OB,OD⊥AB,
∴∠AOD=∠BOD=60°.
∴ ∠OAD=30°.
(2)解:如图84所示,延长CO交AB与点H,作CF⊥AB 于点 F.
∵OD⊥AB,
∴OD∥CF.
∴∠HOD=∠HCF=∠E.
设DH=2x,则OH=3x.
∴在 Rt△ODH中,根据勾股定理得 解得
∵∠HOD=∠E,∠ODH=∠HCE,
∴ △HOD∽△HEC.
一、知识梳理
【例】如图10-1所示,△ABC是⊙O 的内接三角形,∠BAC=75°,∠ABC=45°. 连接AO并延长,交⊙O 于点D,连接BD. 过点C作⊙O的切线,交BA的延长线于点 E.
(1)求证:AD∥EC;
(2)若AB=12,求线段EC的长.
证明:(1)如图10-2所示,连接OC.
∵CE与⊙O 相切于点 C,
∴ ∠OCE=90°.
∵∠ABC=45°,
∴∠AOC=90°.
∵∠AOC+∠OCE=180°,
∴AD∥EC.
(2)如图10-3所示,过点A 作AF⊥EC交EC于点 F.
∵∠BAC=75°,∠ABC=45°,
∴∠ACB=60°.
∴ ∠D=∠ACB=60°.
∵AD是⊙O的直径,
∴∠ABD=90°.
∵AB=12,
∵AF⊥EC,∠OCE=90°,∠AOC=90°,OA=OC,
∴ 四边形 OAFC 是正方形.
二、分层练习
1. 如图10-4所示,AB为⊙O 的直径,点 C在⊙O 上,CO⊥AB 于点O,弦CD与AB 相交于点 F,在AB的延长线上取一点 E,使EF=ED,过点A作⊙O 的切线交 ED的延长线于点 G.
(1)求证:GE 是⊙O 的切线;
(2)若OF:OB=1:3,⊙O 的半径为3,求DE和AG的长.
2. 如图10-5所示,AB是⊙O的直径,AE 是⊙O 的切线,点C 为直线AE 延长线上的一点,连接OC,交⊙O于点D,连接BD并延长,交线段AC于点E.
(1)求证:∠CDE=∠CAD;
(2)若 求⊙O 的半径.
3.如图10-6所示,AB是⊙O的直径,点 C是⊙O 上异于点A,B的一点,连接AC,BC,点D在BA的延长线上,且 ,点E在DC的延长线上,且
(1)求证:DC是⊙O 的切线;
(2)若 求 DA 的长.
4. 如图10-7所示,AB 是⊙O 的直径,PA,PC分别与⊙O 相切于点A,C,PC交AB的延长线于点 D, 的延长线于点 E.
(1)求证:
(2)若 求⊙O的半径.
5. 如图10-8所示,在平行四边形ABCD中,. ,以AD为直径作⊙O,⊙O恰好经过点 B.
(1)求证:BC是⊙O的切线;
(2)点E在⊙O上,ED与AD相交于点M,连接ED并延长,交BC的延长线于点 F.若 求线段ED的长.
6. 如图10-9所示,在等腰三角形ABC中,A ,以BC 为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为点 F,交CB的延长线于点E.
(1)求证:直线 EF是⊙O 的切线;
(2)连接BG,求 BG的长及cos∠E的值.
7. 如图10-10所示,在△ABC中,AB=AC,以AB为直径的⊙O 分别交AC,BC于点D,E,点 F在AC的延长线上,且
(1)求证:直线BF 是⊙O 的切线;
(2)若 求AD的长.
8. 如图10-11所示,在 中,AD平分 ,交 BC 于点 D,以AD为直径作⊙O交AC于点F,点 B恰好落在⊙O上,过点D 作⊙O的切线DE,交AC于点E,连接DF.
(1)求证:
(2)若 求线段DE的长.
9. 如图10-12所示,⊙O是 的外接圆,点D 在 CB的延长线上,连接AD,作 于点E,交AD于点F,且. ,连接BF.
(1)求证:AD 是⊙O 的切线;
求线段BF的长.
10. 如图10-13所示,锐角三角形ABC内接于⊙O,( 于点D,连接OC.
(1)若∠ACB=60°,求证:
(2)过点 C 作⊙O 的切线,交AB 的延长线于点 E.若 求OC的长.
第10节 圆中的计算(2)
1.(1)证明:连接OD,如图73所示.
∵OC=OD,
∴∠C=∠ODC.
∵OC⊥AB,
∴∠COF=90°.
∴∠C+∠CFO=90°.
∴∠ODC+∠CFO=90°.
∵EF=ED,
∴ ∠EFD=∠EDF.
∵∠CFO=∠EFD,
∴∠ODC+∠EDF=90°.
∴∠ODE=90°.
∵OD为⊙O的半径,
∴GE为⊙O的切线.
(2)解:∵OF:OB=1:3,⊙O 的半径为3,
∴OF=1.
设DE=x,则EF=x,OE=1+x.
∵在Rt△ODE中,( 即 解得x=4,
∴DE=4,OE=5.
∵AG为⊙O的切线,
∴AG⊥AE.
∴∠GAE=90°.
又∵∠OED=∠GEA,
∴ Rt△EOD∽Rt△EGA.
即 解得AG=6.
2.(1)证明:∵AE是⊙O 的切线, (2)解:∵∠B=∠DAE,
∴∠OAE=90°.
∴∠OAD+∠CAD=90°.
∵AB是⊙O的直径, ∵∠CDE=∠CAD,∠C=∠C,
∴∠ODB+∠ODA=∠ADB=90°. ∴△CDE∽△CAD.
∴ ∠B+∠OAD=90°.
∵OB=OD, ∵CD=4,
∴∠B=∠ODB.
∵∠ODB=∠CDE, 解得
∴ ∠CDE=∠CAD. 设⊙O 的半径为r.
∴在Rt△OAC中,即 解得r=14.
3.(1)证明:连接OC,如图74所示.
∵AB是⊙O的直径,
∴∠OCD=∠DCA+∠ACO=90°.
∵OC是⊙O的半径,
∴DC是⊙O 的切线.
(2)解:∵BE⊥DC,
∴∠BEC=90°.
∴∠BEC=∠OCD.
∴OC∥BE.
∴∠EBD=∠COD.
∴在 Rt△OCD中,
设
∴OA=OB=OC=2a.
∴DA=OD-OA=3a-2a=a.
∵∠EBD=∠COD,∠BEC=∠OCD,
∴△DEB∽△DCO.
即 解得
4. (1)证明:∵PA,PC分别与⊙O 相切于点A,C,DE⊥PO的延长线于点 E,
∴∠APE=∠EPD,∠PAO=∠DEO=90°.
又∵∠AOP=∠EOD,
∴△PAO∽△DEO.
∴∠APO=∠EDO.
∴∠EPD=∠EDO.
(2)如图75所示,连接OC.
∵ PA,PC分别与⊙O 相切于点A,C,
∴ PA=PC=6,∠PAO=∠PCO=90°.
设OC=3x,DC=4x,则OD=5x,AD=OA+OD=8x,PD=PC+CD=6+4x.
∵在 Rt△PAD中, 即 解得 (舍去),
∴OC=3.
∴⊙O 的半径为3.
5.(1)证明:如图76所示,连接BD,OB.
∵∠A=45°,OA=OB,
∴∠ABO=45°.
∴ ∠AOB=90°.
∵四边形ABCD 是平行四边形,
∴AD∥BC.
∴∠OBC=∠AOB=90°.
∴BC⊥OB,
又∵OB 是⊙O的半径,
∴BC为⊙O的切线.
(2)解:如图77所示,过点 D 作DG⊥BC于点G,则∠DGB=∠DGF=90°,DG∥OB.
∵OB=OD,∠OBG=∠DGF=∠BOD=90°,
∴四边形 BODG是正方形,
∵在Rt△DGF中,
∴由切割线定理可知,
即 解得
6.(1)证明:如图78所示,连接OD,CD.
∵BC是⊙O的直径,
∴CD⊥AB.
∵AC=BC,AB=12,
∴AD=BD=6.
∵点O 为BC的中点,
∴OD∥AC.
∵DF⊥AC,
∴OD⊥EF.
∴EF是⊙O的切线.
(2)解:如图79所示,连接BG.
∵ BC是⊙O 的直径,
∴∠BDC=90°.
∵BG⊥AC,DF⊥AC,
∴BG∥EF.
∴∠E=∠CBG.
7.(1)证明:连接AE,∠1和∠2如图80所示.
∵AB 是⊙O 的直径,
∴∠AEB=90°.
∴ ∠1+∠2=90°.
∵AB=AC,
∴∠1=∠CBF.
∴∠CBF+∠2=90°,即∠ABF=90°.
∵AB 是⊙O的直径,
∴直线 BF是⊙O 的切线.
(2)解:如图81所示,连接BD,过点C作CG⊥AB 于点 G.
∵在 Rt△ABE中,由勾股定理得
∴在 Rt△CBG中,GC=BC·sin∠2=4,GB=BC·cos∠2=2.
∴AG=AB-GB=3.
∵GC∥BF,
∴△AGC∽△ABF.
即
即 解得BD=4.
8.(1)证明:∵DE是⊙O 的切线,AD 是⊙O 的直径,
∴AD⊥DE.
°.
∴∠ADB+∠CDE=90°.
∵AD平分∠BAC,
∴ ∠FAD=∠BAD,
在△FAD 和△BAD中,
∴△FAD≌△BAD(AAS).
∴∠ADF=∠ADB.
∴∠FDE=∠CDE.
(2)解:∵在Rt△ABC中,
∵△FAD≌△BAD,
∴AF=AB=12.
∴CF=AC-AF=20-12=8.
∵在 Rt△CDF中,
∴BD=DF=6.
∴ △EAD∽△DAB.
即 解得AE=15.
9.(1)证明:连接OA,OB,如图82所示.
∵ ∠C+∠AFO=90°,
∴∠OAF=90°.
∴OA⊥AD.
∵OA是⊙O的半径,
∴AD是⊙O的切线.
(2)解:∵由(1)可知,∠AOF=∠C,
∵OE⊥AB,
.
10.(1)证明:如图83所示,连接OA,OB.
∵∠ACB=60°,
∴∠AOB=2∠ACB=120°.
∵OA=OB,OD⊥AB,
∴∠AOD=∠BOD=60°.
∴ ∠OAD=30°.
(2)解:如图84所示,延长CO交AB与点H,作CF⊥AB 于点 F.
∵OD⊥AB,
∴OD∥CF.
∴∠HOD=∠HCF=∠E.
设DH=2x,则OH=3x.
∴在 Rt△ODH中,根据勾股定理得 解得
∵∠HOD=∠E,∠ODH=∠HCE,
∴ △HOD∽△HEC.
同课章节目录
