2025年中考数学几何解题方法复习-- 第11节弧长及扇形面积计算(含解析)
文档属性
| 名称 | 2025年中考数学几何解题方法复习-- 第11节弧长及扇形面积计算(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 455.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 21:46:04 | ||
图片预览


文档简介
第11节弧长及扇形面积计算
一、知识梳理
设⊙O 的半径为R,n°圆心角所对弧长为l,则有
①弧长公式:
②扇形面积公式:
求常见组合图形的周长、面积的几种常用方法:①公式法;②割补法;③拼凑法;④等积变换法.
【例】如图11-1所示,在扇形OAB中,∠AOB=90°,半径OA=6. 将扇形OAB沿过点 B 的直线折叠,使点 O 恰好落在 上的点 D 处,折痕交OA 于点 C,求整个阴影部分的周长和面积.
解:如图11-2所示,连接OD.
∵根据折叠的性质可知,CD=CO,BD=BO,
∠CBD=∠CBO,
∴OB=OD=BD,即△OBD是等边三角形.
∴ ∠DBO=60°.
∵∠AOB=90°,
∴整个阴影部分的周长 整个阴影部分的面积
二、分层练习
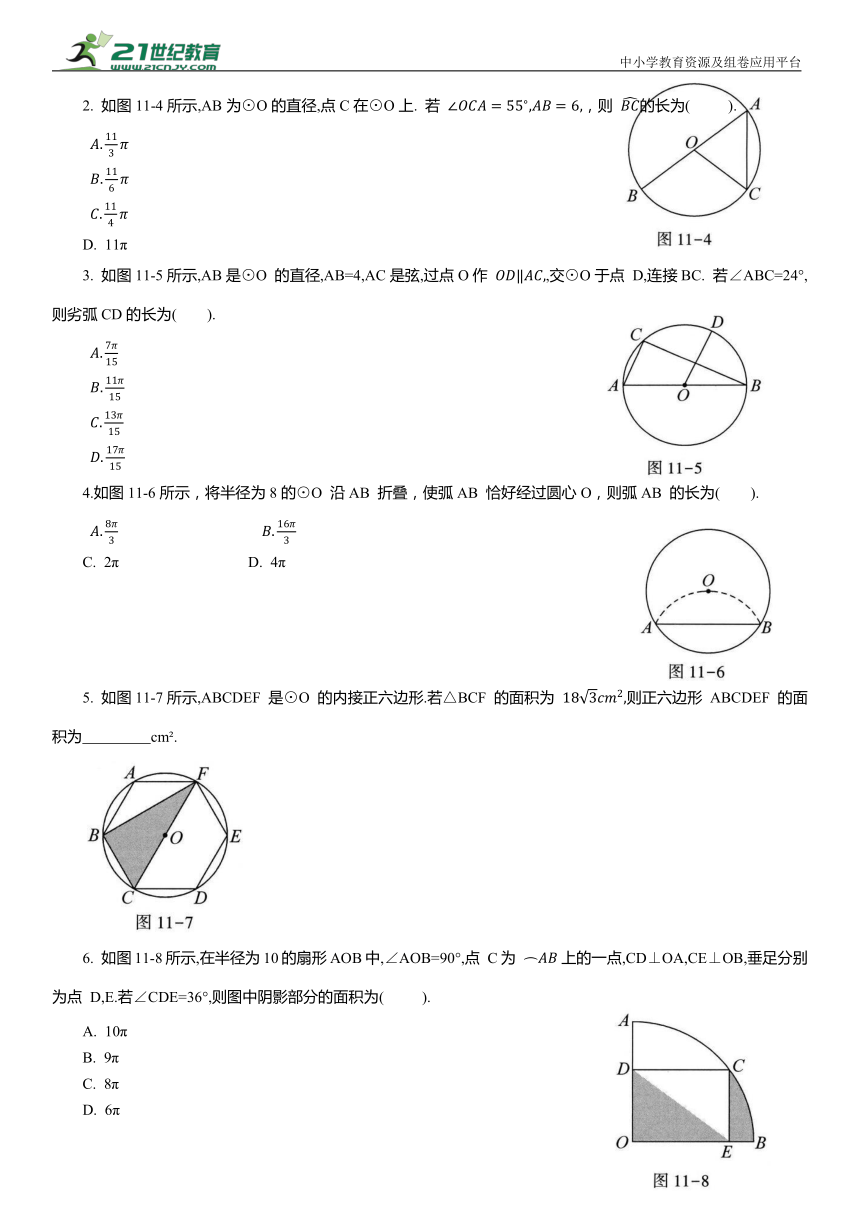
1. 如图11-3所示,AB是⊙O 的直径,AB=4,∠BOC=120°,CD⊥AB,则劣弧AD的长为 .
2. 如图11-4所示,AB为⊙O的直径,点C在⊙O上. 若 ,则 的长为( ).
D. 11π
3. 如图11-5所示,AB是⊙O 的直径,AB=4,AC是弦,过点O作 ,交⊙O于点 D,连接BC. 若∠ABC=24°,则劣弧CD的长为( ).
4.如图11-6所示,将半径为8的⊙O 沿AB 折叠,使弧AB 恰好经过圆心O,则弧AB 的长为( ).
C. 2π D. 4π
5. 如图11-7所示,ABCDEF 是⊙O 的内接正六边形.若△BCF 的面积为 则正六边形 ABCDEF 的面积为 cm .
6. 如图11-8所示,在半径为10的扇形AOB中,∠AOB=90°,点 C为 上的一点,CD⊥OA,CE⊥OB,垂足分别为点 D,E.若∠CDE=36°,则图中阴影部分的面积为( ).
A. 10π
B. 9π
C. 8π
D. 6π
7.如图11-9所示,正方形ABCD的边长为2,点 O 为正方形ABCD对角线的交点,点E,F分别为BC,AD的中点.以点C为圆心,2为半径作圆弧BD,再分别以点E,F为圆心,1为半径作圆弧BO,OD,则图中阴影部分的面积为( ).
A. π-1
B. π-2
C. π-3
D. 4-π
8.图11-10所示是一圆柱形管道的横截面,管道直径为12cm,里面存有3cm深的污水,则污水部分(阴影部分)的面积是 ( c m^{2}.
9. 如图11-11 所示,AB 是⊙O 的直径,CD,EF 是⊙O 的弦,且 AB=10,CD=6,EF=8,则图中阴影部分的面积为 .
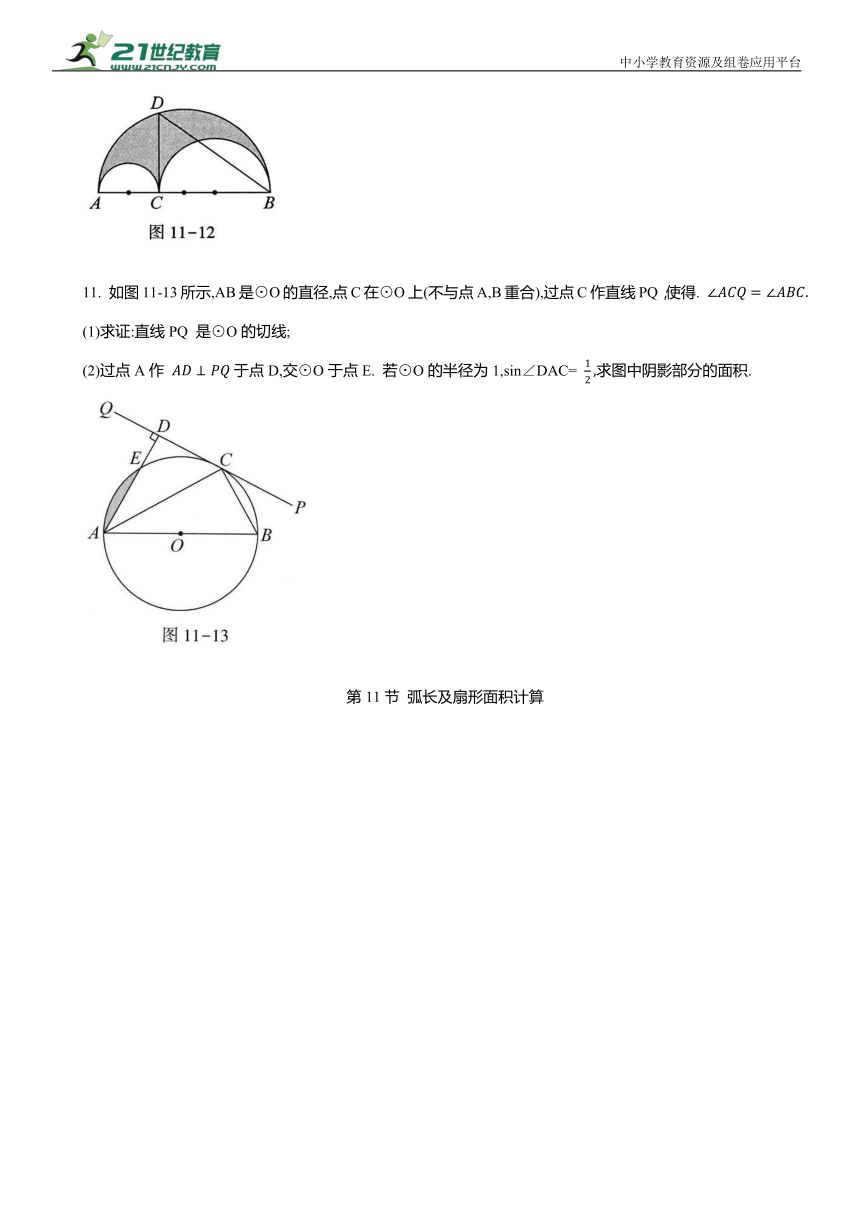
10. 如图11-12所示,点C 是线段AB上的任一点,分别以AB,AC,BC为直径在线段AB的同侧作半圈,则这三个半圆所围成的图形被阿基米德称为“鞋匠刀形”(即图中阴影部分).当“鞋匠刀形”的面积等于以BC为直径的半圆的面积时,过点C作CD⊥AB,交圆周于点D,连接BD,则 的值为 .
11. 如图11-13所示,AB是⊙O的直径,点C在⊙O上(不与点A,B重合),过点C作直线PQ,使得.
(1)求证:直线PQ 是⊙O的切线;
(2)过点A作 于点D,交⊙O于点E. 若⊙O的半径为1,sin∠DAC= 求图中阴影部分的面积.
中小学教育资源及组卷应用平台
第11节 弧长及扇形面积计算
1. 解:∵∠BOC=120°,
∴ ∠AOC=60°.
∵AB是⊙O 的直径,AB=4,CD⊥AB,
∴∠AOD=∠AOC=60°.
∵OA=2,
∴劣弧AD 的长
3. 解:如图85所示,连接OC.
∵AB 是⊙O 的直径,
∴∠ACB=90°.
∵∠ABC=24°,
∵AC∥OD,
∴∠BOD=∠A=66°.
∵AB=4,
∴ 劣弧 CD的长
故选 B.
2. 解:∵∠OCA=55°,OA=OC,
∴∠A=55°.
∴∠BOC=2∠A=110°.
∵AB=6,
∴BO=3.
的长
故选 B.
4. 解:如图86所示,作OC⊥AB于点 D,交⊙O于点C,连接OA,OB.
∵OC⊥AB,
∴∠ODA=90°.
∵将半径为8的⊙O 沿AB 折叠,弧AB 恰好经过圆心O,
∴∠OAD=30°.
∴ ∠AOD=60°.
∴ ∠AOB=120°.
∴弧AB长
故选 B.
☆欲穷千里目,更上一层楼
5. 解:如图87所示,连接AO,BO.
∵六边形ABCDEF 是正六边形,
即
6. 解:如图88所示,连接OC.
∵∠AOB=90°,CD⊥OA,CE⊥OB,
∴四边形 CDOE 是矩形.
∴CD∥OE.
∴∠DEO=∠CDE=36°.
∵由矩形的性质可知,△DOE≌△CEO,
∴∠COB=∠DEO=36°.
∴图中阴影部分的面积=扇形OBC 的面积
故选 A.
7. 解:如图89所示,连接BD.
由题意可得, 故选 B.
8.解:如图90所示,圆心为点O,液面所在弦为AB,液面最低点为点 D,连接OD 交AB 于点 C.
∵由题意可知,OC⊥AB,
∴AC=BC.
∵OA=6cm,CD=3cm,
∴∠AOC=60°.
∴截面上有污水部分的面积
9. 解: 如图91所示,连接OC,OD,OE,DG,OF,延长CO交⊙O于点G.
∵CG是⊙O的直径,
∴∠CDG=90°.
∵EF=8,
∴DG=EF.
扇形OEF·
∵AB∥CD∥EF,
∴ S阴影=S扇形OCD+S扇形OEF=S扇形OCD+S扇形ODG=S半圆= π×5 = π.
10. 解:连接AD,如图92 所示.
设AC=2r,BC=2R.
∵“鞋匠刀形”的面积等于以 BC为直径的半圆的面积, 即
∴R=2r.
∵AB 为直径,
∴∠ADB=90°.
∴ ∠A+∠B=90°.
∵CD⊥AB,
∴∠DCB=∠DCA=90°.
∴ ∠B+∠BDC=90°.
∴∠A=∠BDC.
又∵∠DCB=∠DCA,
∴△ACD∽△DCB.
即 解得
11.(1)证明:连接OC,如图93 所示.
∵AB是⊙O的直径,
∴OC⊥PQ.
∵OC是⊙O的半径,
∴直线 PQ 是⊙O 的切线.
(2)解:连接OE,OC,过点O作( 于点F,如图94所示.
∴∠DAC=30°.
∵AD⊥PQ,OC⊥PQ,
∴OC∥AD.
∴ ∠ACO=∠DAC=30°.
∵OA=OC,
∴∠OAC=∠OCA=30°.
∴∠DAO=60°.
∵OA=OE,
∴△OAE是等边三角形.
∴∠AOE=60°,OA=OE=AE=1.
∵OF⊥AE,
一、知识梳理
设⊙O 的半径为R,n°圆心角所对弧长为l,则有
①弧长公式:
②扇形面积公式:
求常见组合图形的周长、面积的几种常用方法:①公式法;②割补法;③拼凑法;④等积变换法.
【例】如图11-1所示,在扇形OAB中,∠AOB=90°,半径OA=6. 将扇形OAB沿过点 B 的直线折叠,使点 O 恰好落在 上的点 D 处,折痕交OA 于点 C,求整个阴影部分的周长和面积.
解:如图11-2所示,连接OD.
∵根据折叠的性质可知,CD=CO,BD=BO,
∠CBD=∠CBO,
∴OB=OD=BD,即△OBD是等边三角形.
∴ ∠DBO=60°.
∵∠AOB=90°,
∴整个阴影部分的周长 整个阴影部分的面积
二、分层练习
1. 如图11-3所示,AB是⊙O 的直径,AB=4,∠BOC=120°,CD⊥AB,则劣弧AD的长为 .
2. 如图11-4所示,AB为⊙O的直径,点C在⊙O上. 若 ,则 的长为( ).
D. 11π
3. 如图11-5所示,AB是⊙O 的直径,AB=4,AC是弦,过点O作 ,交⊙O于点 D,连接BC. 若∠ABC=24°,则劣弧CD的长为( ).
4.如图11-6所示,将半径为8的⊙O 沿AB 折叠,使弧AB 恰好经过圆心O,则弧AB 的长为( ).
C. 2π D. 4π
5. 如图11-7所示,ABCDEF 是⊙O 的内接正六边形.若△BCF 的面积为 则正六边形 ABCDEF 的面积为 cm .
6. 如图11-8所示,在半径为10的扇形AOB中,∠AOB=90°,点 C为 上的一点,CD⊥OA,CE⊥OB,垂足分别为点 D,E.若∠CDE=36°,则图中阴影部分的面积为( ).
A. 10π
B. 9π
C. 8π
D. 6π
7.如图11-9所示,正方形ABCD的边长为2,点 O 为正方形ABCD对角线的交点,点E,F分别为BC,AD的中点.以点C为圆心,2为半径作圆弧BD,再分别以点E,F为圆心,1为半径作圆弧BO,OD,则图中阴影部分的面积为( ).
A. π-1
B. π-2
C. π-3
D. 4-π
8.图11-10所示是一圆柱形管道的横截面,管道直径为12cm,里面存有3cm深的污水,则污水部分(阴影部分)的面积是 ( c m^{2}.
9. 如图11-11 所示,AB 是⊙O 的直径,CD,EF 是⊙O 的弦,且 AB=10,CD=6,EF=8,则图中阴影部分的面积为 .
10. 如图11-12所示,点C 是线段AB上的任一点,分别以AB,AC,BC为直径在线段AB的同侧作半圈,则这三个半圆所围成的图形被阿基米德称为“鞋匠刀形”(即图中阴影部分).当“鞋匠刀形”的面积等于以BC为直径的半圆的面积时,过点C作CD⊥AB,交圆周于点D,连接BD,则 的值为 .
11. 如图11-13所示,AB是⊙O的直径,点C在⊙O上(不与点A,B重合),过点C作直线PQ,使得.
(1)求证:直线PQ 是⊙O的切线;
(2)过点A作 于点D,交⊙O于点E. 若⊙O的半径为1,sin∠DAC= 求图中阴影部分的面积.
中小学教育资源及组卷应用平台
第11节 弧长及扇形面积计算
1. 解:∵∠BOC=120°,
∴ ∠AOC=60°.
∵AB是⊙O 的直径,AB=4,CD⊥AB,
∴∠AOD=∠AOC=60°.
∵OA=2,
∴劣弧AD 的长
3. 解:如图85所示,连接OC.
∵AB 是⊙O 的直径,
∴∠ACB=90°.
∵∠ABC=24°,
∵AC∥OD,
∴∠BOD=∠A=66°.
∵AB=4,
∴ 劣弧 CD的长
故选 B.
2. 解:∵∠OCA=55°,OA=OC,
∴∠A=55°.
∴∠BOC=2∠A=110°.
∵AB=6,
∴BO=3.
的长
故选 B.
4. 解:如图86所示,作OC⊥AB于点 D,交⊙O于点C,连接OA,OB.
∵OC⊥AB,
∴∠ODA=90°.
∵将半径为8的⊙O 沿AB 折叠,弧AB 恰好经过圆心O,
∴∠OAD=30°.
∴ ∠AOD=60°.
∴ ∠AOB=120°.
∴弧AB长
故选 B.
☆欲穷千里目,更上一层楼
5. 解:如图87所示,连接AO,BO.
∵六边形ABCDEF 是正六边形,
即
6. 解:如图88所示,连接OC.
∵∠AOB=90°,CD⊥OA,CE⊥OB,
∴四边形 CDOE 是矩形.
∴CD∥OE.
∴∠DEO=∠CDE=36°.
∵由矩形的性质可知,△DOE≌△CEO,
∴∠COB=∠DEO=36°.
∴图中阴影部分的面积=扇形OBC 的面积
故选 A.
7. 解:如图89所示,连接BD.
由题意可得, 故选 B.
8.解:如图90所示,圆心为点O,液面所在弦为AB,液面最低点为点 D,连接OD 交AB 于点 C.
∵由题意可知,OC⊥AB,
∴AC=BC.
∵OA=6cm,CD=3cm,
∴∠AOC=60°.
∴截面上有污水部分的面积
9. 解: 如图91所示,连接OC,OD,OE,DG,OF,延长CO交⊙O于点G.
∵CG是⊙O的直径,
∴∠CDG=90°.
∵EF=8,
∴DG=EF.
扇形OEF·
∵AB∥CD∥EF,
∴ S阴影=S扇形OCD+S扇形OEF=S扇形OCD+S扇形ODG=S半圆= π×5 = π.
10. 解:连接AD,如图92 所示.
设AC=2r,BC=2R.
∵“鞋匠刀形”的面积等于以 BC为直径的半圆的面积, 即
∴R=2r.
∵AB 为直径,
∴∠ADB=90°.
∴ ∠A+∠B=90°.
∵CD⊥AB,
∴∠DCB=∠DCA=90°.
∴ ∠B+∠BDC=90°.
∴∠A=∠BDC.
又∵∠DCB=∠DCA,
∴△ACD∽△DCB.
即 解得
11.(1)证明:连接OC,如图93 所示.
∵AB是⊙O的直径,
∴OC⊥PQ.
∵OC是⊙O的半径,
∴直线 PQ 是⊙O 的切线.
(2)解:连接OE,OC,过点O作( 于点F,如图94所示.
∴∠DAC=30°.
∵AD⊥PQ,OC⊥PQ,
∴OC∥AD.
∴ ∠ACO=∠DAC=30°.
∵OA=OC,
∴∠OAC=∠OCA=30°.
∴∠DAO=60°.
∵OA=OE,
∴△OAE是等边三角形.
∴∠AOE=60°,OA=OE=AE=1.
∵OF⊥AE,
同课章节目录
