2025年中考数学几何解题方法复习-- 第 12 节 点和线到圆的距离最值(含解析)
文档属性
| 名称 | 2025年中考数学几何解题方法复习-- 第 12 节 点和线到圆的距离最值(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 563.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 21:36:12 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第 12 节 点和线到圆的距离最值
一、知识梳理
(一)辅助圆之点到圆的距离最值
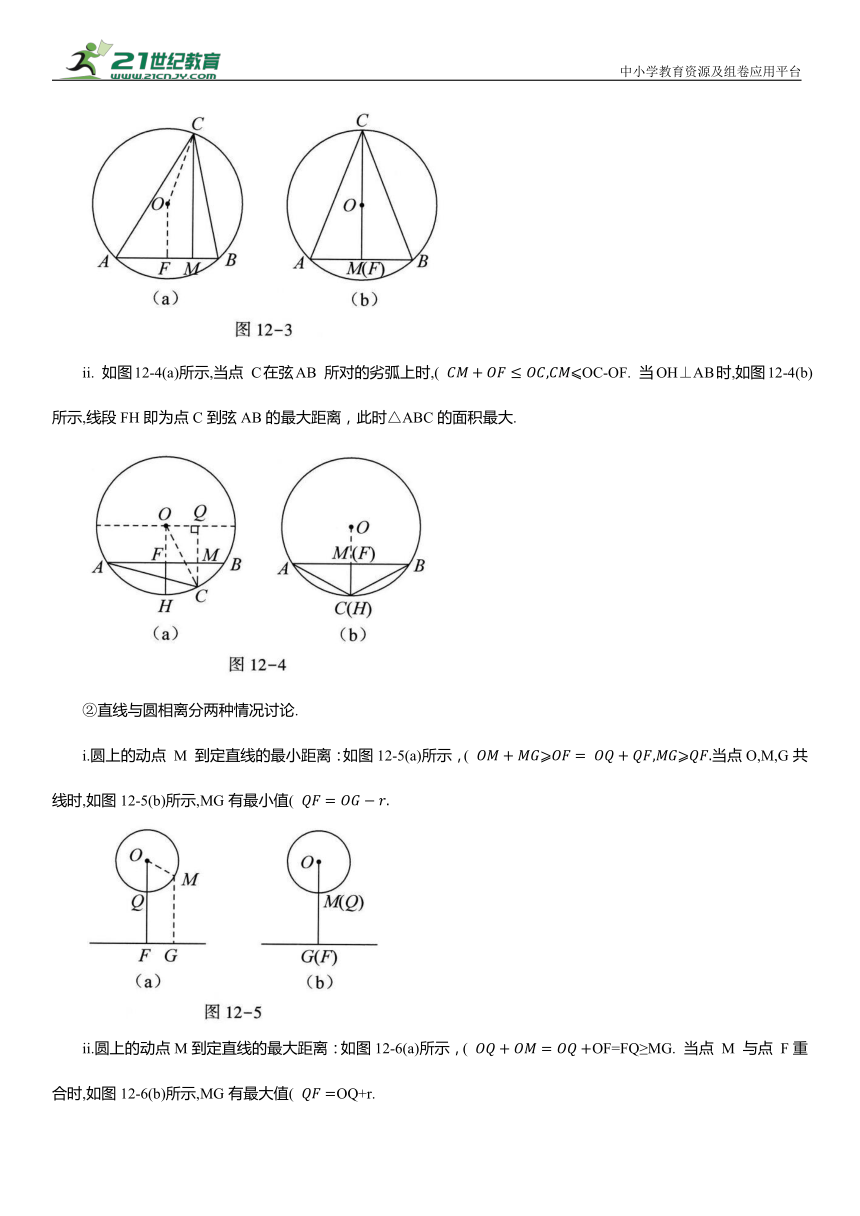
平面内一定点D 和⊙O上动点M 的连线中,当连线过圆心O时,线段DM有最大值和最小值.定点到圆的距离最值分以下情况讨论(设OD=d,⊙O的半径为r):
①当点D在⊙O外时,即d>r,如图12-1(a)、(b)所示,当点D,M,O共线时,线段DM 出现最值,DM的最大值为d+r,DM的最小值为d-r.
②当点D在⊙O内时,即d(二)辅助圆之直线到圆的距离最值
① 直线与圆相交分两种情况讨论.
i.如图12-3(a)所示,当点C在弦AB所对的优弧上运动时,( 当点C,O,F共线时,如图12-3(b)所示,CM⊥AB 且CM 过圆心O,( OF,CM 即为点 C到弦AB的最大距离,此时. 的面积最大.
ii. 如图12-4(a)所示,当点 C在弦AB 所对的劣弧上时,( OC-OF. 当OH⊥AB时,如图12-4(b)所示,线段FH即为点C到弦AB的最大距离,此时△ABC的面积最大.
②直线与圆相离分两种情况讨论.
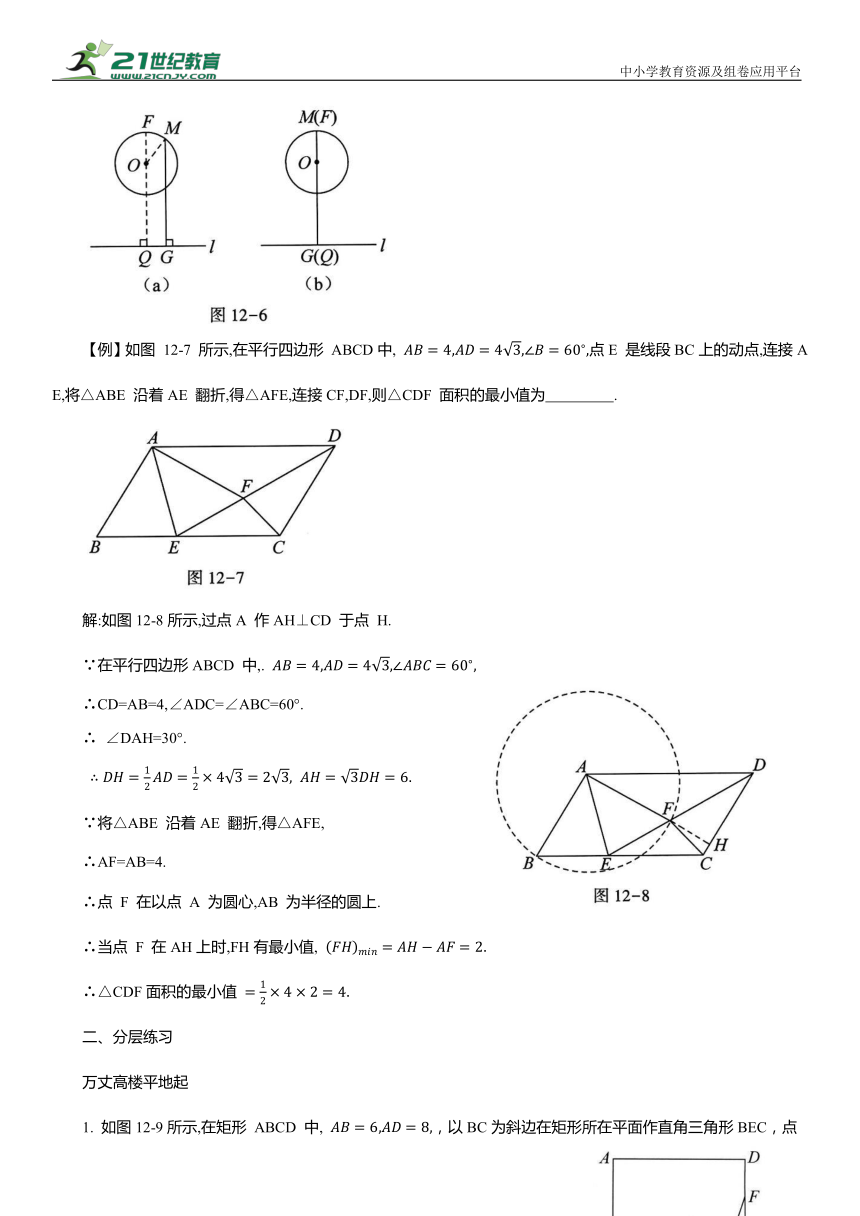
i.圆上的动点 M 到定直线的最小距离:如图12-5(a)所示,( 当点O,M,G共线时,如图12-5(b)所示,MG有最小值(
ii.圆上的动点M到定直线的最大距离:如图12-6(a)所示,( OF=FQ≥MG. 当点 M 与点 F重合时,如图12-6(b)所示,MG有最大值( OQ+r.
【例】如图 12-7 所示,在平行四边形 ABCD中, 点E 是线段BC上的动点,连接AE,将△ABE 沿着AE 翻折,得△AFE,连接CF,DF,则△CDF 面积的最小值为 .
解:如图12-8所示,过点A 作AH⊥CD 于点 H.
∵在平行四边形ABCD 中,.
∴CD=AB=4,∠ADC=∠ABC=60°.
∴ ∠DAH=30°.
∵将△ABE 沿着AE 翻折,得△AFE,
∴AF=AB=4.
∴点 F 在以点 A 为圆心,AB 为半径的圆上.
∴当点 F 在AH上时,FH有最小值,
∴△CDF面积的最小值
二、分层练习
万丈高楼平地起
1. 如图12-9所示,在矩形 ABCD 中, ,以BC为斜边在矩形所在平面作直角三角形BEC,点 F为CD的中点,则EF的最小值为( ).
A. 9
B. 1
C. 2
D. 3
2.如图12-10所示,在平面直角坐标系中,以点A(2,3)为圆心,1为半径作⊙A,以点B(3,4)为圆心,3为半径作⊙B,点M,N分别是⊙A,⊙B上的动点,点 P为x轴上的动点,则PM+PN的最小值为 .
3.解决下列问题:
(1)如图12-11(a)所示,⊙O 的半径为1,圆外一点A到圆心的距离为3,圆上有一动点 B,当点 A,O,B满足条件 时,AB 有最小值为
(2)如图12-11(b)所示,等腰△ABC的两腰长为5,底边长为6,以点A为圆心,2为半径作圆,圆上动点 P到BC的最短距离为 .
(3)如图12-11(c)所示,OA⊥OB,点P,Q分别是射线OA,OB上的两个动点,点 C 是线段 PQ的中点,且PQ=4,则在线段 PQ 滑动的过程中,求点 C 运动形成的路径长,并说明理由.
(4)如图12-11(d)所示,在矩形ABCD中,AB=4,AD=8,点E是AB的中点,点 F 是BC上的一点,把△BEF 沿着EF 翻折,点 B 落在点B'处,求. 的最小值,并说明理由.
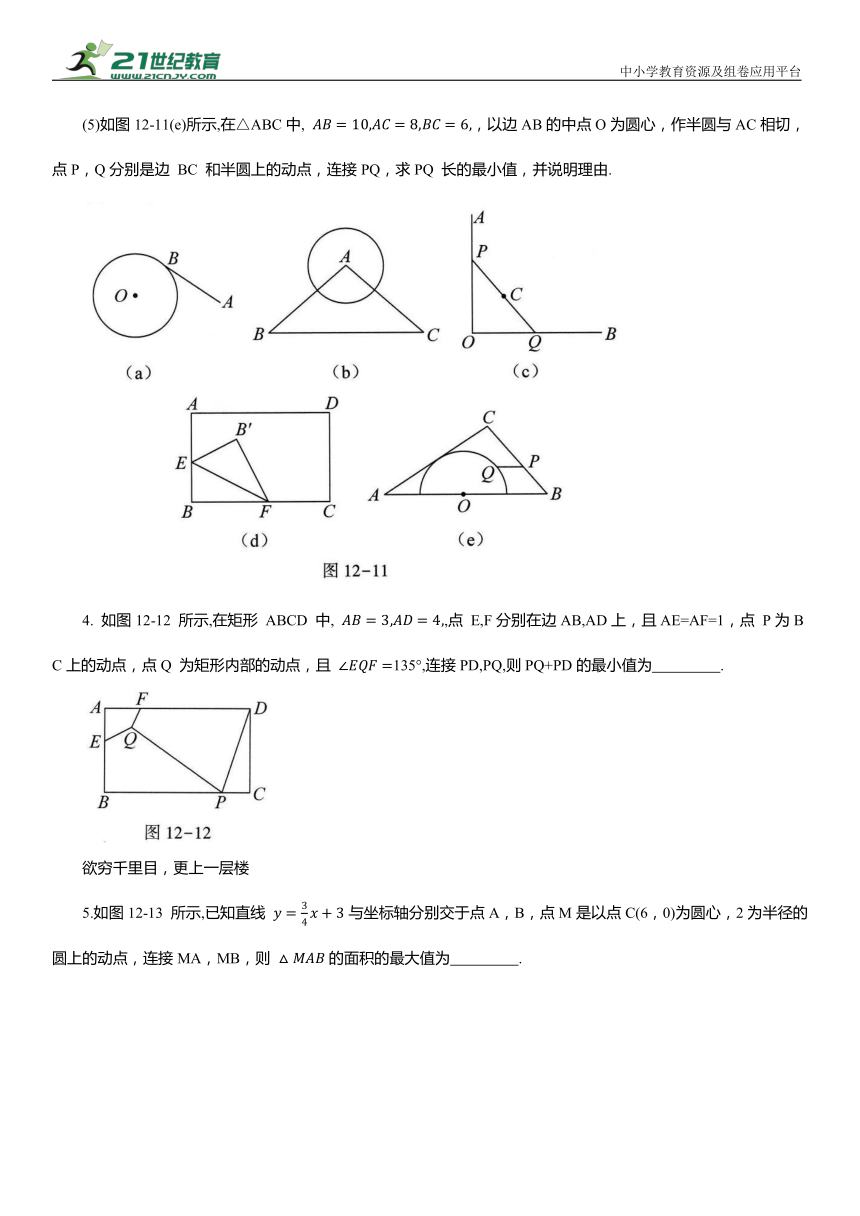
(5)如图12-11(e)所示,在△ABC中, ,以边AB的中点O为圆心,作半圆与AC相切,点P,Q分别是边 BC 和半圆上的动点,连接PQ,求PQ 长的最小值,并说明理由.
4. 如图12-12 所示,在矩形 ABCD 中, ,点 E,F分别在边AB,AD上,且AE=AF=1,点 P为BC上的动点,点Q 为矩形内部的动点,且 135°,连接PD,PQ,则PQ+PD的最小值为 .
欲穷千里目,更上一层楼
5.如图12-13 所示,已知直线 与坐标轴分别交于点A,B,点M是以点C(6,0)为圆心,2为半径的圆上的动点,连接MA,MB,则 的面积的最大值为 .
6. 如图12-14所示,在 Rt△ABC中,∠ABC=90°,AB=8,BC=6,点 D,E分别是线段BA,BC上的动点,且DE=6,点F为DE的中点,则点 F到AC的最短距离为 .
7. 如图12-15 所示,在矩形ABCD 中, ,点E 是AB 边上的一点,且 ,点F是BC边上的任意一点,把 沿EF 翻折,点B 的对应点为点G,连接AG,CG,求四边形AGCD面积的最小值,并求出此时BF的长度.
8.(1)如图12-16(a)所示,线段AB=4,点C 是一个动点,且点 C到点 B 的距离为2,则线段AC长度的最大值为 ;
(2)如图12-16(b)所示,以正方形ABCD的边CD 为直径作半圆O,点E 为半圆O上的一动点.若正方形的边长为2,求AE长度的最大值;
(3)如图12-16(c)所示,某植物园有一块三角形花地ABC,经测量, BC=120m,∠ACB=30°. BC下方有一块空地(空地足够大),为了增加绿化面积,管理员计划在BC下方找一点 P,将该花地扩建为四边形ABPC,扩建后沿AP修一条小路,以便游客观赏.考虑到植物园的整体布局,扩建部分 需满足∠BPC=60°.为了容纳更多的游客,小路AP 的长度要尽可能长,小路AP 的长度是否存在最大值 若存在,求出AP 的最大长度;若不存在,请说明理由.
第12节 点和线到圆的距离最值
1. 解:如图95所示,取BC的中点O,以O为圆心,OC为半径作圆,连接OE,OF.
∵四边形ABCD是矩形,
∴CD=AB=6,BC=AD=8,∠BCD=90°.
∵点F是CD的中点,点O 是BC的中点,
∵点O 是 Rt△BCE 的斜边 BC的中点,
∴OE=OC=4.
∵∠BEC=90°,
∴点 E在以BC为直径的⊙O上,当点O,E,F共线时, 故选 B.
2.解:作⊙A 关于x轴的对称圆⊙A',连接BA',分别交⊙A'和⊙B于点 M,N,交x轴于点 P,此时PM+PN最小,如图96所示.
∵点A的坐标为(2,3),
∴点A'的坐标为(2,-3).
∵点B的坐标为(3,4),
∴ PM+PN的最小值为
3. 解:(1)如图97所示,连接OA,OB.AB≤AO-BO,当点B 在线段AO上时,AB有最小值=3-1=2.
(2)如图98所示,过点A作AH⊥BC于点 H,交⊙A 于点 P,此时点 P到BC的距离最短.
∵AB=AC=5,AH⊥BC,BC=6,
∵AP=2,
∴PH=AH-AP=2.
∴ 圆上动点 P 到 BC 的最短距离为2.
(3)如图99 所示,连接OC.
∵∠POQ=90°,PQ=4,PC=CQ,
∴点 C的运动轨迹是圆弧,
运动路径的长
(4)如图100 所示,连接DE,DB'.
∵四边形ABCD是矩形,
∴∠A=90°.
∵点E是AB的中点,AB=4,
∴ EA=BE=2.
∵AD=8,
∴ DB'的最小值为
(5)当点O,Q,P共线且OP⊥BC时,PQ有最小值,设AC与圆的切点为点D,连接OD,如图101所示.
∵AC是⊙O 的切线,
∴OD⊥AC.
∵AC=8,BC=6,AB=10,
∴∠ACB=90°.
∵AC与圆的切点为点 D,
∴OD∥BC,且点O为AB的中点.
∴OD为△ABC的中位线.
∵同理可得,
∴PQ=OP-OQ=4-3=1.
∴PQ 的最小值为1.
4.解:如图102 所示,连接EF,作点 D 关于 BC的对称点 D',连接.
∵AE=AF=1,∠EAF=90°,
∵∠EQF=135°,
∴点 Q 在以点A 为圆心,AE为半径的圆上运动.
∵点 D 关于 BC 的对称点为点 D',
∴PD=PD'.
∴ PQ+PD=PQ+PD'.
∴ PQ+PD 的最小值为AD'-AE.
∵在 Rt△ADD'中,由勾股定理得
☆☆欲穷千里目,更上一层楼
5. 解:如图103所示,过点C作CD⊥AB 于点 D,延长DC交⊙C于点M.
∵将x=0代入 得y=3,
∴点B的坐标为(0,3).
∴OB=3.
∵将y=0代入 得 解得x=-4.
∴点A的坐标为(-4,0).
∴OA=4.
∴在Rt△ABO中,
∵点 C的坐标为(6,0),
∴AC=10.
∵CD⊥AB,
∴∠CDA=∠AOB=90°.
又∵∠DAC=∠BAO,
∴ △ABO∽△ACD.
即 解得DC=6.
∵⊙C 的半径为2,
6. 解:如图104所示,连接BF,过点B作BH⊥AC于点H,过点 F 作 于点 G.
∵在Rt△ABC中,AB=8,BC=6,
解得
∵在 Rt△DBE中,DE=6,点 F为DE的中点,
∵点F在以点B为圆心,3为半径的圆上,当BF与BH重合时,FG最小,
∴点 F到AC的最短距离
7. 解:∵四边形ABCD 是矩形,
∴CD=AB=3,AD=BC=4,∠ABC=∠D=90°,根据勾股定理得AC=5.
∵AE=2,
∴BE=GE=1.
∴点G是矩形ABCD内部以点E为圆心,BE=1为半径的圆上的一点.设点G到AC的距离为h.
∴要使四边形AGCD的面积最小,则h最小.
当EG⊥AC时,h最小,由折叠知∠EGF=∠ABC=90°.
延长EG交AC于点H,则EH⊥AC,过点F作FM⊥AC于点M,如图105所示.
∵在 Rt△ABC中,
在Rt△AEH中,
∵EH⊥FG,EH⊥AC,
∴ 四边形 FGHM 是矩形.
∵∠FCM=∠ACB,∠CMF=CBA=90°,
∴△CMF∽△CBA.
即 解得CF=1.
∴BF=BC-CF=4-1=3.
答:四边形AGCD 的面积的最小值为 此时BF的长度为3.
会当凌绝顶,一览众山小
8. 解:(1)当点C在线段AB的延长线上时,AC最大,此时AC=AB+BC=4+2=6.
(2)连接AO并延长,交半圆O 于点 F,如图106所示.
∵以正方形ABCD的边CD为直径作半圆O,且正方形的边长为2,
∴∠ADO=90°,AD=2,OD=OC=OF=1.
当点 E 运动到点 F 时,AE 最大,AF 的长度即为AE的最大值.
∵在Rt△AOD中,
(3)作BC的垂直平分线 DE,在BC 下方作∠BCO=30°,射线 CO交DE 于点O,以点O为圆心,OC为半径作⊙O,连接OB,连接AO并延长,交⊙O于点P,则AP为满足条件的小路,过点A作AF⊥OC于点F,如图107所示.
∵∠BCO=30°,∠ACB=30°,
∴∠ACF=60°.
∴在 Rt△ACF中,AF=AC·sin60°=30,CF=AC·cos60°=10
∵ DE 垂直平分BC,BC=120,
∴CE=60,∠OEC=90°.
∵在Rt△AOF中,
∴AP=OA+OP=60+40
答:小路AP 的最大长度为
第 12 节 点和线到圆的距离最值
一、知识梳理
(一)辅助圆之点到圆的距离最值
平面内一定点D 和⊙O上动点M 的连线中,当连线过圆心O时,线段DM有最大值和最小值.定点到圆的距离最值分以下情况讨论(设OD=d,⊙O的半径为r):
①当点D在⊙O外时,即d>r,如图12-1(a)、(b)所示,当点D,M,O共线时,线段DM 出现最值,DM的最大值为d+r,DM的最小值为d-r.
②当点D在⊙O内时,即d
① 直线与圆相交分两种情况讨论.
i.如图12-3(a)所示,当点C在弦AB所对的优弧上运动时,( 当点C,O,F共线时,如图12-3(b)所示,CM⊥AB 且CM 过圆心O,( OF,CM 即为点 C到弦AB的最大距离,此时. 的面积最大.
ii. 如图12-4(a)所示,当点 C在弦AB 所对的劣弧上时,( OC-OF. 当OH⊥AB时,如图12-4(b)所示,线段FH即为点C到弦AB的最大距离,此时△ABC的面积最大.
②直线与圆相离分两种情况讨论.
i.圆上的动点 M 到定直线的最小距离:如图12-5(a)所示,( 当点O,M,G共线时,如图12-5(b)所示,MG有最小值(
ii.圆上的动点M到定直线的最大距离:如图12-6(a)所示,( OF=FQ≥MG. 当点 M 与点 F重合时,如图12-6(b)所示,MG有最大值( OQ+r.
【例】如图 12-7 所示,在平行四边形 ABCD中, 点E 是线段BC上的动点,连接AE,将△ABE 沿着AE 翻折,得△AFE,连接CF,DF,则△CDF 面积的最小值为 .
解:如图12-8所示,过点A 作AH⊥CD 于点 H.
∵在平行四边形ABCD 中,.
∴CD=AB=4,∠ADC=∠ABC=60°.
∴ ∠DAH=30°.
∵将△ABE 沿着AE 翻折,得△AFE,
∴AF=AB=4.
∴点 F 在以点 A 为圆心,AB 为半径的圆上.
∴当点 F 在AH上时,FH有最小值,
∴△CDF面积的最小值
二、分层练习
万丈高楼平地起
1. 如图12-9所示,在矩形 ABCD 中, ,以BC为斜边在矩形所在平面作直角三角形BEC,点 F为CD的中点,则EF的最小值为( ).
A. 9
B. 1
C. 2
D. 3
2.如图12-10所示,在平面直角坐标系中,以点A(2,3)为圆心,1为半径作⊙A,以点B(3,4)为圆心,3为半径作⊙B,点M,N分别是⊙A,⊙B上的动点,点 P为x轴上的动点,则PM+PN的最小值为 .
3.解决下列问题:
(1)如图12-11(a)所示,⊙O 的半径为1,圆外一点A到圆心的距离为3,圆上有一动点 B,当点 A,O,B满足条件 时,AB 有最小值为
(2)如图12-11(b)所示,等腰△ABC的两腰长为5,底边长为6,以点A为圆心,2为半径作圆,圆上动点 P到BC的最短距离为 .
(3)如图12-11(c)所示,OA⊥OB,点P,Q分别是射线OA,OB上的两个动点,点 C 是线段 PQ的中点,且PQ=4,则在线段 PQ 滑动的过程中,求点 C 运动形成的路径长,并说明理由.
(4)如图12-11(d)所示,在矩形ABCD中,AB=4,AD=8,点E是AB的中点,点 F 是BC上的一点,把△BEF 沿着EF 翻折,点 B 落在点B'处,求. 的最小值,并说明理由.
(5)如图12-11(e)所示,在△ABC中, ,以边AB的中点O为圆心,作半圆与AC相切,点P,Q分别是边 BC 和半圆上的动点,连接PQ,求PQ 长的最小值,并说明理由.
4. 如图12-12 所示,在矩形 ABCD 中, ,点 E,F分别在边AB,AD上,且AE=AF=1,点 P为BC上的动点,点Q 为矩形内部的动点,且 135°,连接PD,PQ,则PQ+PD的最小值为 .
欲穷千里目,更上一层楼
5.如图12-13 所示,已知直线 与坐标轴分别交于点A,B,点M是以点C(6,0)为圆心,2为半径的圆上的动点,连接MA,MB,则 的面积的最大值为 .
6. 如图12-14所示,在 Rt△ABC中,∠ABC=90°,AB=8,BC=6,点 D,E分别是线段BA,BC上的动点,且DE=6,点F为DE的中点,则点 F到AC的最短距离为 .
7. 如图12-15 所示,在矩形ABCD 中, ,点E 是AB 边上的一点,且 ,点F是BC边上的任意一点,把 沿EF 翻折,点B 的对应点为点G,连接AG,CG,求四边形AGCD面积的最小值,并求出此时BF的长度.
8.(1)如图12-16(a)所示,线段AB=4,点C 是一个动点,且点 C到点 B 的距离为2,则线段AC长度的最大值为 ;
(2)如图12-16(b)所示,以正方形ABCD的边CD 为直径作半圆O,点E 为半圆O上的一动点.若正方形的边长为2,求AE长度的最大值;
(3)如图12-16(c)所示,某植物园有一块三角形花地ABC,经测量, BC=120m,∠ACB=30°. BC下方有一块空地(空地足够大),为了增加绿化面积,管理员计划在BC下方找一点 P,将该花地扩建为四边形ABPC,扩建后沿AP修一条小路,以便游客观赏.考虑到植物园的整体布局,扩建部分 需满足∠BPC=60°.为了容纳更多的游客,小路AP 的长度要尽可能长,小路AP 的长度是否存在最大值 若存在,求出AP 的最大长度;若不存在,请说明理由.
第12节 点和线到圆的距离最值
1. 解:如图95所示,取BC的中点O,以O为圆心,OC为半径作圆,连接OE,OF.
∵四边形ABCD是矩形,
∴CD=AB=6,BC=AD=8,∠BCD=90°.
∵点F是CD的中点,点O 是BC的中点,
∵点O 是 Rt△BCE 的斜边 BC的中点,
∴OE=OC=4.
∵∠BEC=90°,
∴点 E在以BC为直径的⊙O上,当点O,E,F共线时, 故选 B.
2.解:作⊙A 关于x轴的对称圆⊙A',连接BA',分别交⊙A'和⊙B于点 M,N,交x轴于点 P,此时PM+PN最小,如图96所示.
∵点A的坐标为(2,3),
∴点A'的坐标为(2,-3).
∵点B的坐标为(3,4),
∴ PM+PN的最小值为
3. 解:(1)如图97所示,连接OA,OB.AB≤AO-BO,当点B 在线段AO上时,AB有最小值=3-1=2.
(2)如图98所示,过点A作AH⊥BC于点 H,交⊙A 于点 P,此时点 P到BC的距离最短.
∵AB=AC=5,AH⊥BC,BC=6,
∵AP=2,
∴PH=AH-AP=2.
∴ 圆上动点 P 到 BC 的最短距离为2.
(3)如图99 所示,连接OC.
∵∠POQ=90°,PQ=4,PC=CQ,
∴点 C的运动轨迹是圆弧,
运动路径的长
(4)如图100 所示,连接DE,DB'.
∵四边形ABCD是矩形,
∴∠A=90°.
∵点E是AB的中点,AB=4,
∴ EA=BE=2.
∵AD=8,
∴ DB'的最小值为
(5)当点O,Q,P共线且OP⊥BC时,PQ有最小值,设AC与圆的切点为点D,连接OD,如图101所示.
∵AC是⊙O 的切线,
∴OD⊥AC.
∵AC=8,BC=6,AB=10,
∴∠ACB=90°.
∵AC与圆的切点为点 D,
∴OD∥BC,且点O为AB的中点.
∴OD为△ABC的中位线.
∵同理可得,
∴PQ=OP-OQ=4-3=1.
∴PQ 的最小值为1.
4.解:如图102 所示,连接EF,作点 D 关于 BC的对称点 D',连接.
∵AE=AF=1,∠EAF=90°,
∵∠EQF=135°,
∴点 Q 在以点A 为圆心,AE为半径的圆上运动.
∵点 D 关于 BC 的对称点为点 D',
∴PD=PD'.
∴ PQ+PD=PQ+PD'.
∴ PQ+PD 的最小值为AD'-AE.
∵在 Rt△ADD'中,由勾股定理得
☆☆欲穷千里目,更上一层楼
5. 解:如图103所示,过点C作CD⊥AB 于点 D,延长DC交⊙C于点M.
∵将x=0代入 得y=3,
∴点B的坐标为(0,3).
∴OB=3.
∵将y=0代入 得 解得x=-4.
∴点A的坐标为(-4,0).
∴OA=4.
∴在Rt△ABO中,
∵点 C的坐标为(6,0),
∴AC=10.
∵CD⊥AB,
∴∠CDA=∠AOB=90°.
又∵∠DAC=∠BAO,
∴ △ABO∽△ACD.
即 解得DC=6.
∵⊙C 的半径为2,
6. 解:如图104所示,连接BF,过点B作BH⊥AC于点H,过点 F 作 于点 G.
∵在Rt△ABC中,AB=8,BC=6,
解得
∵在 Rt△DBE中,DE=6,点 F为DE的中点,
∵点F在以点B为圆心,3为半径的圆上,当BF与BH重合时,FG最小,
∴点 F到AC的最短距离
7. 解:∵四边形ABCD 是矩形,
∴CD=AB=3,AD=BC=4,∠ABC=∠D=90°,根据勾股定理得AC=5.
∵AE=2,
∴BE=GE=1.
∴点G是矩形ABCD内部以点E为圆心,BE=1为半径的圆上的一点.设点G到AC的距离为h.
∴要使四边形AGCD的面积最小,则h最小.
当EG⊥AC时,h最小,由折叠知∠EGF=∠ABC=90°.
延长EG交AC于点H,则EH⊥AC,过点F作FM⊥AC于点M,如图105所示.
∵在 Rt△ABC中,
在Rt△AEH中,
∵EH⊥FG,EH⊥AC,
∴ 四边形 FGHM 是矩形.
∵∠FCM=∠ACB,∠CMF=CBA=90°,
∴△CMF∽△CBA.
即 解得CF=1.
∴BF=BC-CF=4-1=3.
答:四边形AGCD 的面积的最小值为 此时BF的长度为3.
会当凌绝顶,一览众山小
8. 解:(1)当点C在线段AB的延长线上时,AC最大,此时AC=AB+BC=4+2=6.
(2)连接AO并延长,交半圆O 于点 F,如图106所示.
∵以正方形ABCD的边CD为直径作半圆O,且正方形的边长为2,
∴∠ADO=90°,AD=2,OD=OC=OF=1.
当点 E 运动到点 F 时,AE 最大,AF 的长度即为AE的最大值.
∵在Rt△AOD中,
(3)作BC的垂直平分线 DE,在BC 下方作∠BCO=30°,射线 CO交DE 于点O,以点O为圆心,OC为半径作⊙O,连接OB,连接AO并延长,交⊙O于点P,则AP为满足条件的小路,过点A作AF⊥OC于点F,如图107所示.
∵∠BCO=30°,∠ACB=30°,
∴∠ACF=60°.
∴在 Rt△ACF中,AF=AC·sin60°=30,CF=AC·cos60°=10
∵ DE 垂直平分BC,BC=120,
∴CE=60,∠OEC=90°.
∵在Rt△AOF中,
∴AP=OA+OP=60+40
答:小路AP 的最大长度为
同课章节目录
