第十八章勾股定理同步练习(含解析)
图片预览
文档简介
中小学教育资源及组卷应用平台
第十八章勾股定理
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.若△ABC是直角三角形,两条直角边分别为5和12,在三角形内有一点D,D到△ABC各边的距离都相等,则这个距离等于( )
A.2 B.3 C.4 D.5
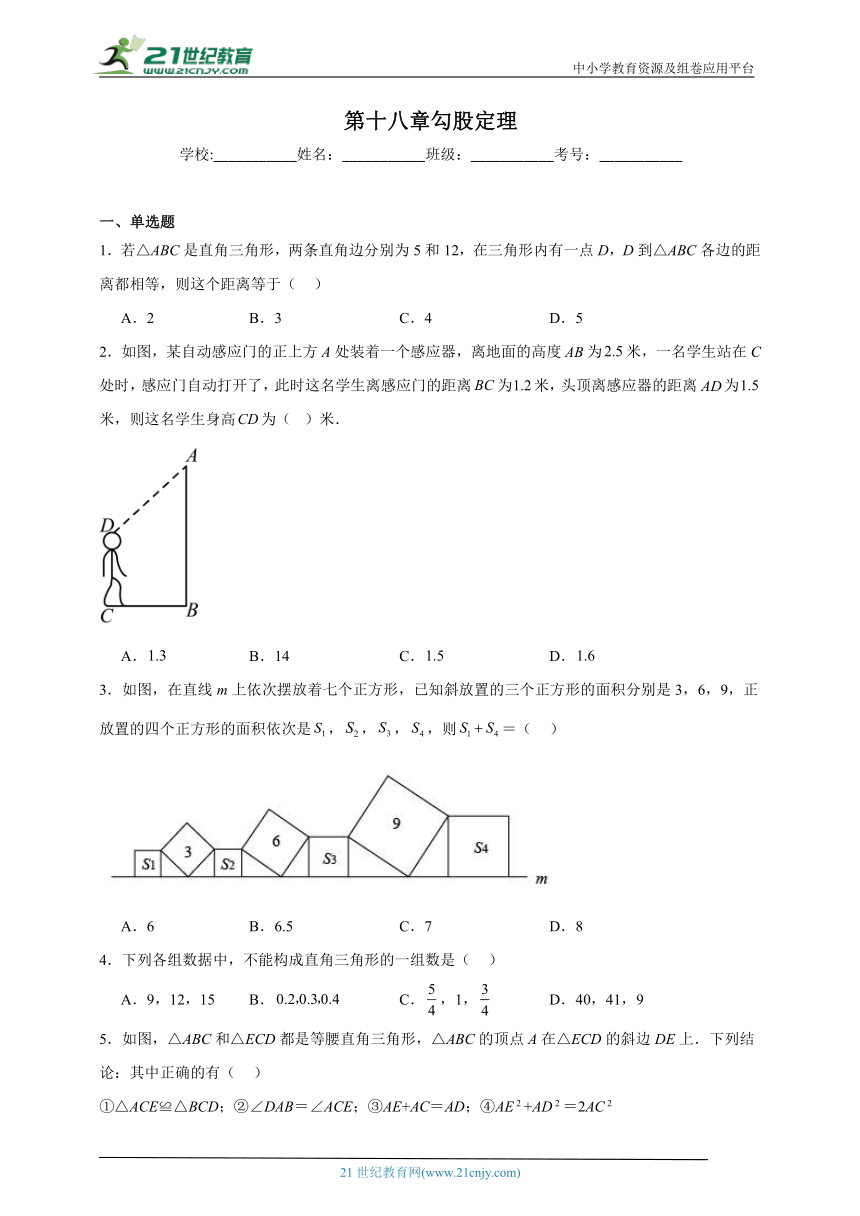
2.如图,某自动感应门的正上方A处装着一个感应器,离地面的高度为米,一名学生站在C处时,感应门自动打开了,此时这名学生离感应门的距离为米,头顶离感应器的距离为米,则这名学生身高为( )米.
A. B.14 C. D.
3.如图,在直线m上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别是3,6,9,正放置的四个正方形的面积依次是,,,,则=( )
A.6 B.6.5 C.7 D.8
4.下列各组数据中,不能构成直角三角形的一组数是( )
A.9,12,15 B. C.,1, D.40,41,9
5.如图,△ABC和△ECD都是等腰直角三角形,△ABC的顶点A在△ECD的斜边DE上.下列结论:其中正确的有( )
①△ACE≌△BCD;②∠DAB=∠ACE;③AE+AC=AD;④AE+AD=2AC
A.1个 B.2个 C.3个 D.4个
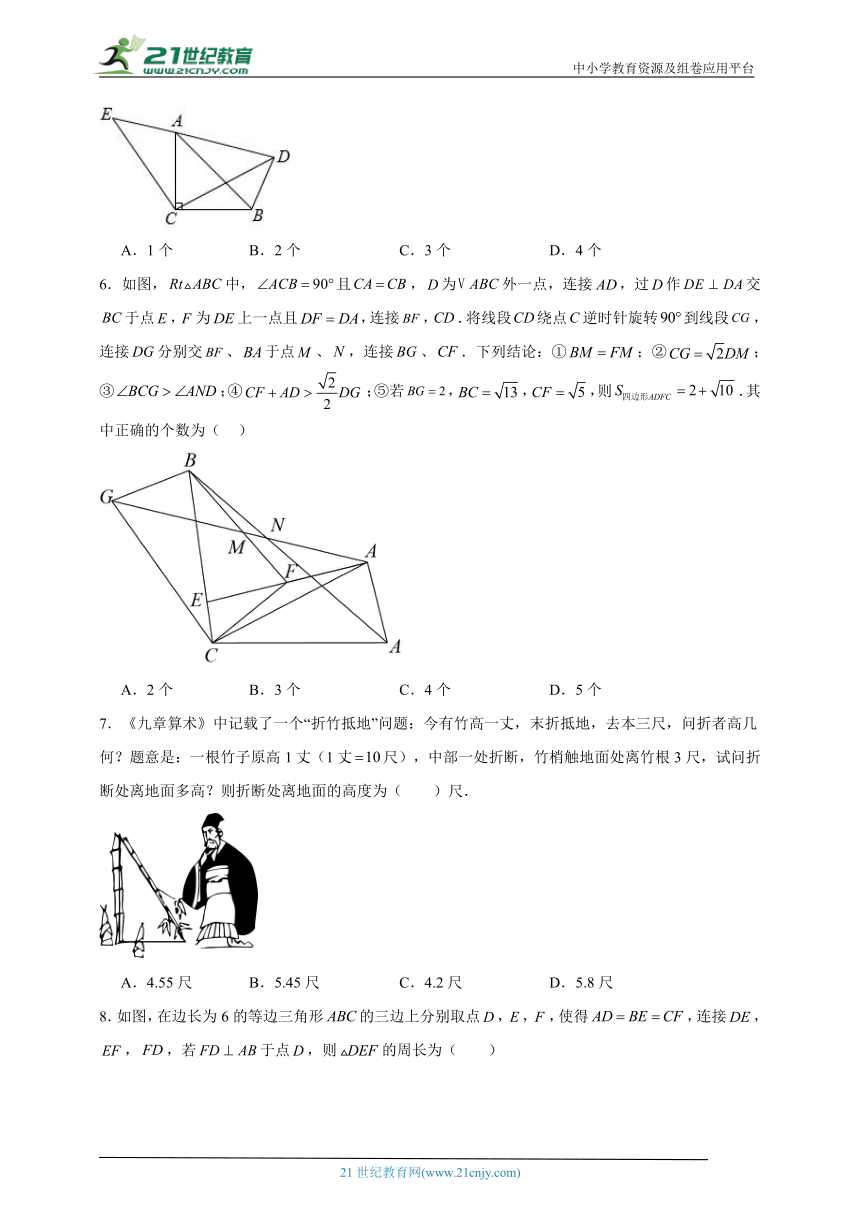
6.如图,中,且,为外一点,连接,过作交于点,为上一点且,连接,.将线段绕点逆时针旋转到线段,连接分别交、于点、,连接、.下列结论:①;②;③;④;⑤若,,,则.其中正确的个数为( )
A.2个 B.3个 C.4个 D.5个
7.《九章算术》中记载了一个“折竹抵地”问题:今有竹高一丈,末折抵地,去本三尺,问折者高几何?题意是:一根竹子原高1丈(1丈尺),中部一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?则折断处离地面的高度为( )尺.
A.4.55尺 B.5.45尺 C.4.2尺 D.5.8尺
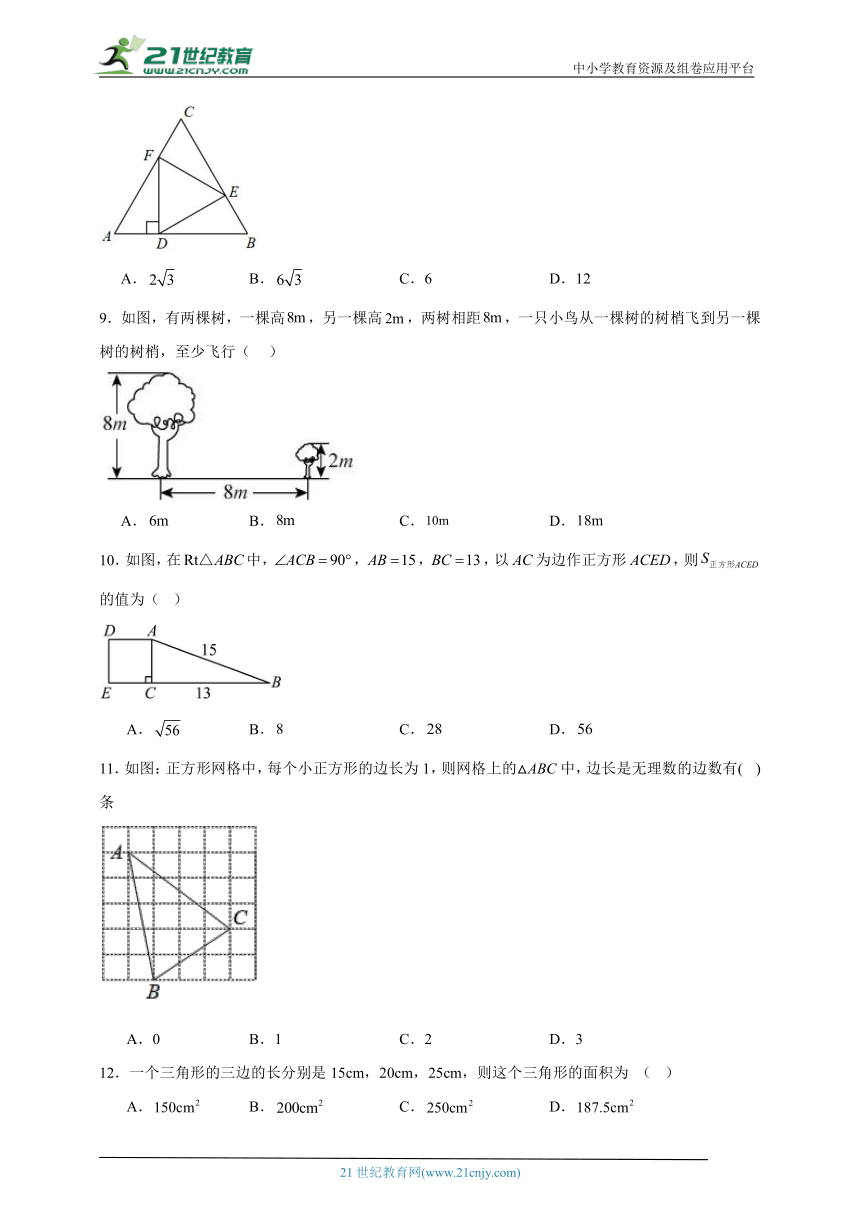
8.如图,在边长为6的等边三角形的三边上分别取点,,,使得,连接,,,若于点,则的周长为( )
A. B. C.6 D.12
9.如图,有两棵树,一棵高,另一棵高,两树相距,一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞行( )
A. B. C. D.
10.如图,在中,,,,以为边作正方形,则的值为( )
A. B. C. D.
11.如图:正方形网格中,每个小正方形的边长为1,则网格上的△ABC中,边长是无理数的边数有( )条
A.0 B.1 C.2 D.3
12.一个三角形的三边的长分别是15cm,20cm,25cm,则这个三角形的面积为 ( )
A. B. C. D.
二、填空题
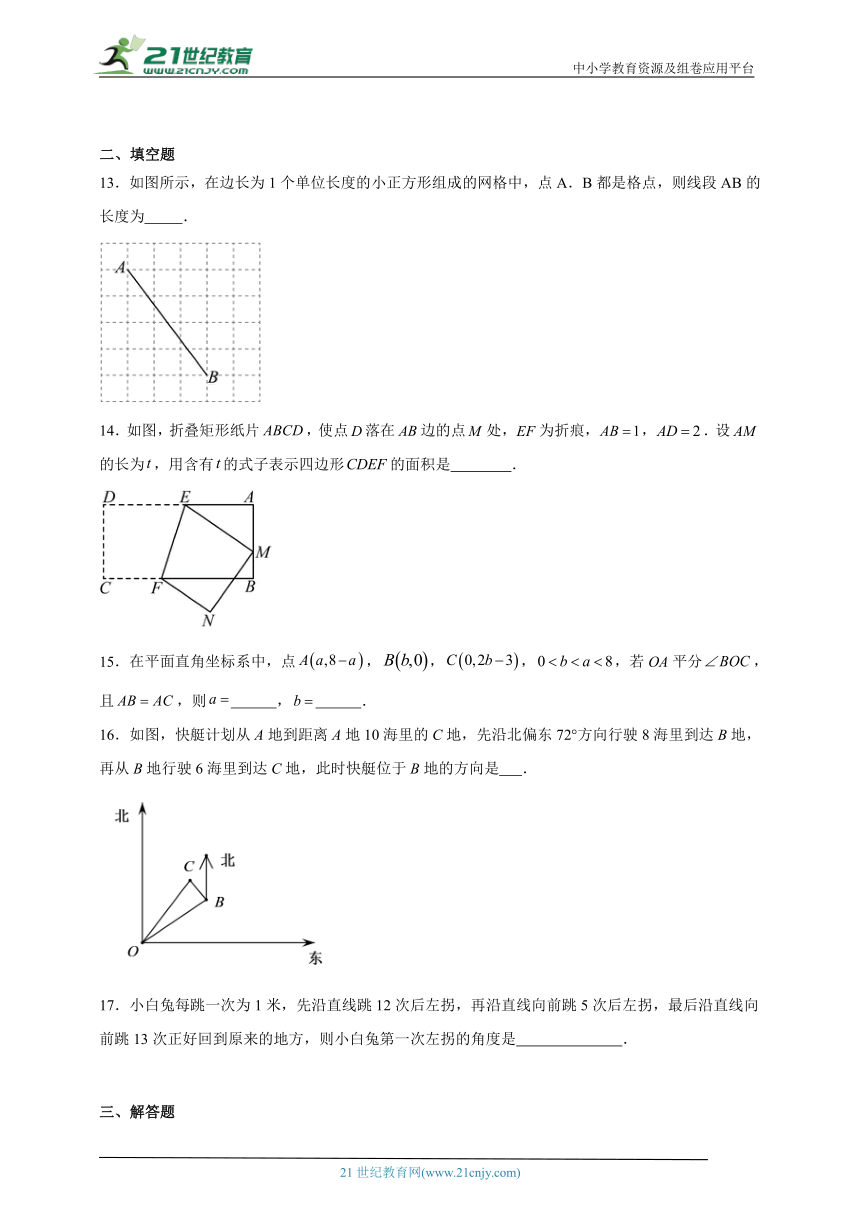
13.如图所示,在边长为1个单位长度的小正方形组成的网格中,点A.B都是格点,则线段AB的长度为 .
14.如图,折叠矩形纸片,使点落在边的点处,为折痕,,.设的长为,用含有的式子表示四边形的面积是 .
15.在平面直角坐标系中,点,,,,若OA平分,且,则 , .
16.如图,快艇计划从A地到距离A地10海里的C地,先沿北偏东72°方向行驶8海里到达B地,再从B地行驶6海里到达C地,此时快艇位于B地的方向是 .
17.小白兔每跳一次为1米,先沿直线跳12次后左拐,再沿直线向前跳5次后左拐,最后沿直线向前跳13次正好回到原来的地方,则小白兔第一次左拐的角度是 .
三、解答题
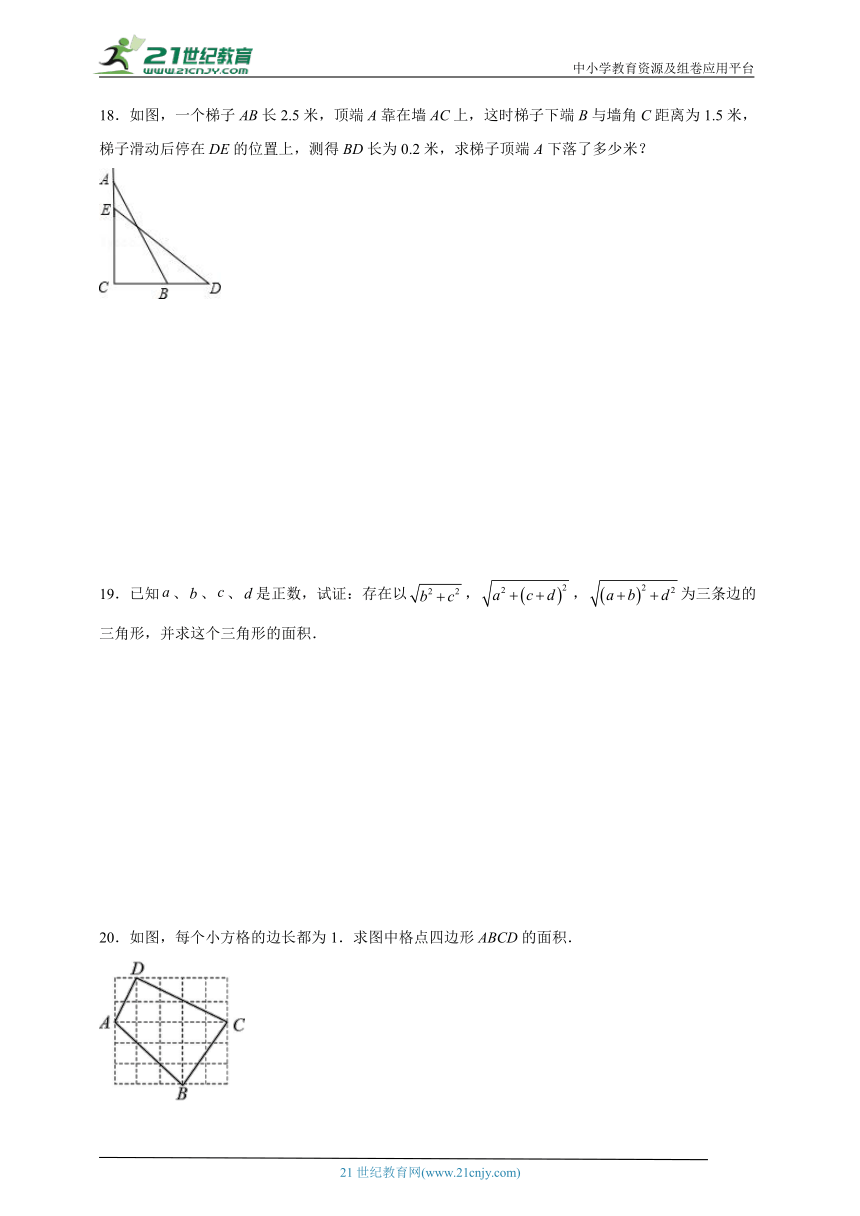
18.如图,一个梯子AB长2.5米,顶端A靠在墙AC上,这时梯子下端B与墙角C距离为1.5米,梯子滑动后停在DE的位置上,测得BD长为0.2米,求梯子顶端A下落了多少米?
19.已知、、、是正数,试证:存在以,,为三条边的三角形,并求这个三角形的面积.
20.如图,每个小方格的边长都为1.求图中格点四边形ABCD的面积.
21.如图,在四边形中,,,.连接,探究三者之间的数量关系,并说明理由.
22.勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜的发现,当两个全等的直角三角形如图摆放时,都可以用“面积法”来证明,请你利用如图证明勾股定理(其中∠DAB=90°)求证:a2+b2=c2.
23.一个零件的形状如图,按规定这个零件中与都应为直角,工人师傅量得零件各边尺寸:,,,,,这个零件符合要求吗?
24.根据勾股定理知识迁移,完成下列应用.
(1)如图1,分别以直角三角形的三边为直径向外侧作半圆,则它们的面积,,之间满足的等量关系是________;
(2)应用:如图2,直角三角形的两条直角边长分别为a,b,斜边长为c,分别以三边为直径作半圆,若,,求图中阴影部分的面积.
《第十八章勾股定理》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A D A B C C A B C D
题号 11 12
答案 C A
1.A
【分析】根据勾股定理列式求出斜边的长度,然后根据三角形的面积不变列式求解即可.
【详解】解:的两条直角边分别为和,
斜边,
设D到各边的距离都相等为,
则,
解得.
故选:A.
【点睛】本题考查了角平分线的性质,勾股定理的应用,本题利用三角形的面积列式求解更加简便.
2.D
【分析】本题考查了勾股定理的应用,正确作出辅助线构造直角三角形是解题的关键.过点D作于E,得到,米,由勾股定理得出,进而得到米,即可得出答案.
【详解】解:过点D作于E,如图所示:
则,米,
在中,米,
由勾股定理得
(米),
∴(米),
∴米.
故选:D.
3.A
【分析】运用勾股定理可知,每两个相邻的正方形面积和都等于中间斜放的正方形面积,据此即可解答.
【详解】解:如图,观察发现,
∵,
∴,,
∴,
在与中,,
∴(AAS),
∴,
∵,
∴,
即,
同理,,
则,
则.
故选:A.
【点睛】此题考查了全等三角形的判定以及性质、勾股定理.解决本题的关键是得到.
4.B
【分析】先求出两小边的平方和,再求出最长边的平方,最后看看是否相等即可.
【详解】解:A、∵,∴能构成直角三角形,故此选项不符合题意;
B、∵,∴不能构成直角三角形,故此选项符合题意;
C、∵,∴能构成直角三角形,故此选项不符合题意;
D、∵,∴能构成直角三角形,故此选项不符合题意;
故选B.
【点睛】本题主要考查了勾股定理逆定理,关键是掌握如果三角形的三边长a,b,c满足,那么这个三角形就是直角三角形.
5.C
【分析】根据等腰直角三角形的性质得到CA=CB,∠CAB=∠CBA=45°,CD=CE,∠E=∠CDE=45°,则可根据“SAS”证明△ACE≌△BCD,于是可对①进行判断;利用三角形外角性质得到∠DAB+∠BAC=∠E+∠ACE,加上∠CAB=∠E=45°,则可得对②进行判断;由全等三角形得性质和等边三角形得性质得出③不正确;证出△ADB是直角三角形,由勾股定理得出④正确.
【详解】解:∵△ABC和△ECD都是等腰直角三角形,
∴CA=CB,∠CAB=∠CBA=45°,CD=CE,∠E=∠CDE=45°,
∵∠ACE+∠ACD=∠ACD+∠BCD,
∴∠ACE=∠BCD,
在△ACE和△BCD中,
,
∴△ACE≌△BCD(SAS),所以①正确;
∵∠DAC=∠E+∠ACE,即∠DAB+∠BAC=∠E+∠ACE,
而∠CAB=∠E=45°,
∴∠DAB=∠ACE,所以②正确;
在AD上截取DF=AE,连接CF,如图所示,
在△ACE和△FCD中,
∴△ACE△FCD(SAS),
∴AC=FC,
当,△ACF是等边三角形,
则AC=AF,此时AE+AC=DF+AF=AD,
但无法求证,
故③不正确;
由①得,△ACE≌△BCD,
∴AE=BD,CEA=CDB=45°,
∴ADB=CDB+EDC=90°,
∴△ADB是直角三角形,
∴,
∴,
∵△ABC是等腰直角三角形,
∴,
∴,故④正确;
故选C.
【点睛】本题考查了全等三角形得判定和性质、等腰直角三角形的性质、勾股定理和直角三角形的判定和性质,解决本题的关键是掌握全等三角形的判定和性质.
6.C
【分析】先证明,得到对应边相等,对应角相等,依次得出①正确和③错误,由等腰直角三角形的性质和勾股定理,得出②正确,由三角形的三边关系,可以得出④正确,利用勾股定理逆定理和三角形面积公式即可判定⑤正确.
【详解】解:∵,,
∴,
又∵且,
∴,
∴,,
∴
∵,
∴,
∴,
∴,
∴,
又∵,,
∴,
∴,,故①正确;
∵,
∴,
∴,故②正确;
,即,故④正确;
∵,,,
∴,
∴,故③错误;
如图,连接,
若,,,
∴,
∴,即,
∴,
∴,
∴,故⑤正确;
故选:C.
【点睛】本题综合考查了全等三角形的判定与性质、勾股定理及其逆定理、等腰直角三角形等内容,解决本题的关键是能正确分析图形中的相等关系,能在相等的边和角中进行转化,能构造直角三角形进行求解等.
7.A
【分析】本题主要考查勾股定理,理解题意,找出等量关系列出方程是解题关键.设折断处离地面的高度为x尺,根据勾股定理结合题意,列出方程求解即可.
【详解】解:设折断处离地面的高度为x尺,
结合勾股定理可得出:,
解得:.
∴折断处离地面的高度为4.55尺.
故选A.
8.B
【分析】先证明,得到等边,设,则,解得x,在中,计算即可.
【详解】∵等边三角形,,
∴,,
∴,
∴,
∴,
∴,
∵,,
∴,,
设,则,
∵,
解得,
∴,
∴的周长为,
故选B.
【点睛】本题考查了等边三角形的判定和性质,三角形全等的判定和性质,直角三角形的性质,勾股定理,熟练掌握勾股定理,等边三角形的判定,直角三角形的性质是解题的关键.
9.C
【分析】根据题意,画出图形,连接AC,过点C作CE⊥AB于点E,可得CE=BD=8m,在中,由勾股定理,即可求解.
【详解】解:根据题意,画出图形,如下图:连接AC,过点C作CE⊥AB于点E,
根据题意得:AB=8m,CD=2m,BD=8m,AB⊥BD,CD⊥BD,
则四边形BDCE是矩形,
∴CE=BD=8m,
在中,由勾股定理得:
,
即小鸟至少飞行10m.
故选:C.
【点睛】本题主要考查了勾股定理的应用,解题的关键是将现实问题建立数学模型,运用数学知识进行求解.
10.D
【分析】本题考查了勾股定理,根据勾股定理求得,即可求解.
【详解】解:.
故选:D.
11.C
【分析】根据勾股定理求出三边的长度,再判断即可.
【详解】解:由勾股定理得:AC==5,是有理数;
BC==,是无理数;
AB==,是无理数;
即网格上的△ABC三边中,边长为无理数的边数有2条.
故选:C.
【点睛】本题考查了无理数和勾股定理,能正确根据勾股定理求出三边的长度是解此题的关键.
12.A
【分析】根据勾股定理的逆定理可得该三角形为直角三角形,然后再利用三角形的面积公式即可求解.
【详解】∵15 +20 =25 ,
∴此三角形是直角三角形,
∴三角形的面积为=.
故答案为A.
【点睛】本题考查三角形面积公式和勾股定理的逆定理,解题的关键是掌握三角形面积公式和勾股定理的逆定理.
13.5
【分析】如图,构造直角三角形,再利用勾股定理求得斜边.
【详解】如图,做AC⊥BC,在Rt△ABC中,AB==
【点睛】此题主要考查勾股定理的应用.
14.
【分析】首先根据题意可以设DE=EM=x,在三角形AEM中用勾股定理进一步可以用t表示出x,再可以设CF=y,连接MF,所以BF=2 y,在三角形MFN与三角形MFB中利用共用斜边,根据勾股定理可求出用t表示出y,进而根据四边形的面积公式可以求出答案.
【详解】设DE=EM=x,
∴,
∴x=,
设CF=y,连接FM,
∴BF=2 y,
又∵FN= y,NM=1,
∴,
∴y=,
∴四边形的面积为:= 1,
故答案为:.
【点睛】本题主要考查了勾股定理的综合运用,熟练掌握技巧性就可得出答案.
15. 4 或
【分析】先证明点A在第一象限的平分线上,得到,则,再由,利用勾股定理得到,利用因式分解得到,根据两个数的乘积为0,那么两个乘数中至少有一个为0解方程即可.
【详解】解:∵,,,
∴点A在第一象限,点B在x正半轴,
∵OA平分,,
∴点C在y轴正半轴,
∴点A在第一象限的平分线上,
∴,
∴,
∵,
∴,
∴,
∴,
∴或,
∴或,
故答案为:4;或.
【点睛】本题主要考查了坐标与图形,勾股定理,因式分解的应用,正确求出是解题的关键.
16.北偏西18°
【分析】由AC=10海里,AB=8海里,BC=6海里得AC2=AB2+BC2,根据勾股定理的逆定理得到∠ABC=90°,再利用平行线的性质和互余的性质得到∠1,求得∠2.
【详解】解:如图,过点B作BD∥AE,
∵AC=10海里,AB=8海里,BC=6海里,
∴AC2=AB2+BC2,
∴△ABC为直角三角形,即∠ABC=90°,
又∵B点在A的北偏东72°方向,
∴∠1=90°-72°=18°,
∴∠2=∠1=18°,
即快艇位于B的北偏西18°的方向上.
故答案为:北偏西18°.
【点睛】本题考查了利用勾股定理解决航海问题:在每点处画上东南西北,然后利用平行线的性质和勾股定理的逆定理的应用.
17.
【详解】由题意得:小白兔第一次跳12米,第二次跳5米,第三次跳13米;
∵米,
而13 =169,刚好符合直角三角形中勾股定理的逆定理,且第一次和第二次跳的距离为直角边.
故小白兔第一次左拐的角度是90°.
18.0.17米
【分析】根据已知条件,在Rt△ABC中,根据勾股定理求得AC=2米,在Rt△CDE中,根据勾股定理求得CE≈1.83米,即可求得AE=0.17米,即梯子的顶端下滑了0.17米.
【详解】在Rt△ABC中,AB=2.5米,BC=1.5米,
由勾股定理可得AC=2米,
在Rt△ECD中,AB=DE=2.5米,CD=1.5+0.2=1.7米,
由勾股定理可得EC=米,
∴AE=AC-CE=2-1.83=0.17米
答:梯子顶端A下落了约0.17m.
【点睛】本题考查了勾股定理的应用,运用勾股定理求得AC和CE的长是解决问题的关键.
19.
【分析】构造矩形,使得,,在上取一点A使得,,在上取一点B使得,,连接、、得到.然后利用勾股定理证明这个三角形符合条件,再利用分割法求出面积即可.
【详解】解:构造矩形,使得,,在上取一点A使得,,在上取一点B使得,,连接、、得到.
四边形是矩形,
∴,
∴,,
,
∴存在以,,为三条边的三角形.
∴这个三角形的面积为:
.
【点睛】本题考查二次根式的应用、勾股定理、矩形的性质等知识,解题的关键是学会利用数形结合的思想解决问题,属于中考压轴题.
20.
【分析】用正方形的面积减去四个三角形的面积即可.
【详解】S四边形ABCD=5×5-×1×2-×4×2-×3×2-×3×3=25-1-4-3-=.
【点睛】本题考查了求不规则图形的面积,利用整体减局部的方法是解题关键.
21..理由见解析
【分析】本题考查了等边三角形的性质,全等三角形的判定与性质,四边形内角和定理,勾股定理
在四边形中,由四边形内角和定理即可得出结果,以为边向下作等边三角形,有等边三角形的性质得出,证出,证明,得出,证出,再由勾股定理即可得出结论.
【详解】.
理由如下:
如图,以BD为边向下作等边三角形BDQ.
∵,
∴.
∵,,
∴,
∴,.
∵,
∴,
∴.
∵,,
∴.
22.见解析
【分析】利用大图形的面积等于几个小图形的面积和,化简整理即可得到勾股定理表达式.
【详解】证明:如图,连接DB,过点D作BC边上的高DF,则DF=EC=b﹣a,
∵S四边形ADCB=S△ACD+S△ABC=b2+ab,
又∵S四边形ADCB=S△ADB+S△DCB=c2+a(b﹣a),
∴b2+ab=c2+a(b﹣a),
,
即a2+b2=c2.
【点睛】本题考查了勾股定理的证明,用两种方法表示出四边形的面积是解本题的关键.
23.这个零件符合要求
【分析】本题考查勾股定理的逆定理,解题的关键是根据勾股定理的逆定理证明为直角三角形是直角三角形.
【详解】解:连接.
在中,,
所以为直角三角形,,
在中,
所以是直角三角形,,
因此这个零件符合要求.
24.(1)S1+S2=S3
(2)阴影部分的面积为6
【详解】(1)如图,设直角三角形的三边长分别为,则
故答案为:
(2)设直角三角形为S4,直角三角形三边为直径的半圆的面积,,
∵直角边a=3,斜边c=5
∴,则
∴阴影部分的面积S=S1+S2+S4-S3=S4=6
【点睛】本题考查了勾股定理,掌握勾股定理是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第十八章勾股定理
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.若△ABC是直角三角形,两条直角边分别为5和12,在三角形内有一点D,D到△ABC各边的距离都相等,则这个距离等于( )
A.2 B.3 C.4 D.5
2.如图,某自动感应门的正上方A处装着一个感应器,离地面的高度为米,一名学生站在C处时,感应门自动打开了,此时这名学生离感应门的距离为米,头顶离感应器的距离为米,则这名学生身高为( )米.
A. B.14 C. D.
3.如图,在直线m上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别是3,6,9,正放置的四个正方形的面积依次是,,,,则=( )
A.6 B.6.5 C.7 D.8
4.下列各组数据中,不能构成直角三角形的一组数是( )
A.9,12,15 B. C.,1, D.40,41,9
5.如图,△ABC和△ECD都是等腰直角三角形,△ABC的顶点A在△ECD的斜边DE上.下列结论:其中正确的有( )
①△ACE≌△BCD;②∠DAB=∠ACE;③AE+AC=AD;④AE+AD=2AC
A.1个 B.2个 C.3个 D.4个
6.如图,中,且,为外一点,连接,过作交于点,为上一点且,连接,.将线段绕点逆时针旋转到线段,连接分别交、于点、,连接、.下列结论:①;②;③;④;⑤若,,,则.其中正确的个数为( )
A.2个 B.3个 C.4个 D.5个
7.《九章算术》中记载了一个“折竹抵地”问题:今有竹高一丈,末折抵地,去本三尺,问折者高几何?题意是:一根竹子原高1丈(1丈尺),中部一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?则折断处离地面的高度为( )尺.
A.4.55尺 B.5.45尺 C.4.2尺 D.5.8尺
8.如图,在边长为6的等边三角形的三边上分别取点,,,使得,连接,,,若于点,则的周长为( )
A. B. C.6 D.12
9.如图,有两棵树,一棵高,另一棵高,两树相距,一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞行( )
A. B. C. D.
10.如图,在中,,,,以为边作正方形,则的值为( )
A. B. C. D.
11.如图:正方形网格中,每个小正方形的边长为1,则网格上的△ABC中,边长是无理数的边数有( )条
A.0 B.1 C.2 D.3
12.一个三角形的三边的长分别是15cm,20cm,25cm,则这个三角形的面积为 ( )
A. B. C. D.
二、填空题
13.如图所示,在边长为1个单位长度的小正方形组成的网格中,点A.B都是格点,则线段AB的长度为 .
14.如图,折叠矩形纸片,使点落在边的点处,为折痕,,.设的长为,用含有的式子表示四边形的面积是 .
15.在平面直角坐标系中,点,,,,若OA平分,且,则 , .
16.如图,快艇计划从A地到距离A地10海里的C地,先沿北偏东72°方向行驶8海里到达B地,再从B地行驶6海里到达C地,此时快艇位于B地的方向是 .
17.小白兔每跳一次为1米,先沿直线跳12次后左拐,再沿直线向前跳5次后左拐,最后沿直线向前跳13次正好回到原来的地方,则小白兔第一次左拐的角度是 .
三、解答题
18.如图,一个梯子AB长2.5米,顶端A靠在墙AC上,这时梯子下端B与墙角C距离为1.5米,梯子滑动后停在DE的位置上,测得BD长为0.2米,求梯子顶端A下落了多少米?
19.已知、、、是正数,试证:存在以,,为三条边的三角形,并求这个三角形的面积.
20.如图,每个小方格的边长都为1.求图中格点四边形ABCD的面积.
21.如图,在四边形中,,,.连接,探究三者之间的数量关系,并说明理由.
22.勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜的发现,当两个全等的直角三角形如图摆放时,都可以用“面积法”来证明,请你利用如图证明勾股定理(其中∠DAB=90°)求证:a2+b2=c2.
23.一个零件的形状如图,按规定这个零件中与都应为直角,工人师傅量得零件各边尺寸:,,,,,这个零件符合要求吗?
24.根据勾股定理知识迁移,完成下列应用.
(1)如图1,分别以直角三角形的三边为直径向外侧作半圆,则它们的面积,,之间满足的等量关系是________;
(2)应用:如图2,直角三角形的两条直角边长分别为a,b,斜边长为c,分别以三边为直径作半圆,若,,求图中阴影部分的面积.
《第十八章勾股定理》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A D A B C C A B C D
题号 11 12
答案 C A
1.A
【分析】根据勾股定理列式求出斜边的长度,然后根据三角形的面积不变列式求解即可.
【详解】解:的两条直角边分别为和,
斜边,
设D到各边的距离都相等为,
则,
解得.
故选:A.
【点睛】本题考查了角平分线的性质,勾股定理的应用,本题利用三角形的面积列式求解更加简便.
2.D
【分析】本题考查了勾股定理的应用,正确作出辅助线构造直角三角形是解题的关键.过点D作于E,得到,米,由勾股定理得出,进而得到米,即可得出答案.
【详解】解:过点D作于E,如图所示:
则,米,
在中,米,
由勾股定理得
(米),
∴(米),
∴米.
故选:D.
3.A
【分析】运用勾股定理可知,每两个相邻的正方形面积和都等于中间斜放的正方形面积,据此即可解答.
【详解】解:如图,观察发现,
∵,
∴,,
∴,
在与中,,
∴(AAS),
∴,
∵,
∴,
即,
同理,,
则,
则.
故选:A.
【点睛】此题考查了全等三角形的判定以及性质、勾股定理.解决本题的关键是得到.
4.B
【分析】先求出两小边的平方和,再求出最长边的平方,最后看看是否相等即可.
【详解】解:A、∵,∴能构成直角三角形,故此选项不符合题意;
B、∵,∴不能构成直角三角形,故此选项符合题意;
C、∵,∴能构成直角三角形,故此选项不符合题意;
D、∵,∴能构成直角三角形,故此选项不符合题意;
故选B.
【点睛】本题主要考查了勾股定理逆定理,关键是掌握如果三角形的三边长a,b,c满足,那么这个三角形就是直角三角形.
5.C
【分析】根据等腰直角三角形的性质得到CA=CB,∠CAB=∠CBA=45°,CD=CE,∠E=∠CDE=45°,则可根据“SAS”证明△ACE≌△BCD,于是可对①进行判断;利用三角形外角性质得到∠DAB+∠BAC=∠E+∠ACE,加上∠CAB=∠E=45°,则可得对②进行判断;由全等三角形得性质和等边三角形得性质得出③不正确;证出△ADB是直角三角形,由勾股定理得出④正确.
【详解】解:∵△ABC和△ECD都是等腰直角三角形,
∴CA=CB,∠CAB=∠CBA=45°,CD=CE,∠E=∠CDE=45°,
∵∠ACE+∠ACD=∠ACD+∠BCD,
∴∠ACE=∠BCD,
在△ACE和△BCD中,
,
∴△ACE≌△BCD(SAS),所以①正确;
∵∠DAC=∠E+∠ACE,即∠DAB+∠BAC=∠E+∠ACE,
而∠CAB=∠E=45°,
∴∠DAB=∠ACE,所以②正确;
在AD上截取DF=AE,连接CF,如图所示,
在△ACE和△FCD中,
∴△ACE△FCD(SAS),
∴AC=FC,
当,△ACF是等边三角形,
则AC=AF,此时AE+AC=DF+AF=AD,
但无法求证,
故③不正确;
由①得,△ACE≌△BCD,
∴AE=BD,CEA=CDB=45°,
∴ADB=CDB+EDC=90°,
∴△ADB是直角三角形,
∴,
∴,
∵△ABC是等腰直角三角形,
∴,
∴,故④正确;
故选C.
【点睛】本题考查了全等三角形得判定和性质、等腰直角三角形的性质、勾股定理和直角三角形的判定和性质,解决本题的关键是掌握全等三角形的判定和性质.
6.C
【分析】先证明,得到对应边相等,对应角相等,依次得出①正确和③错误,由等腰直角三角形的性质和勾股定理,得出②正确,由三角形的三边关系,可以得出④正确,利用勾股定理逆定理和三角形面积公式即可判定⑤正确.
【详解】解:∵,,
∴,
又∵且,
∴,
∴,,
∴
∵,
∴,
∴,
∴,
∴,
又∵,,
∴,
∴,,故①正确;
∵,
∴,
∴,故②正确;
,即,故④正确;
∵,,,
∴,
∴,故③错误;
如图,连接,
若,,,
∴,
∴,即,
∴,
∴,
∴,故⑤正确;
故选:C.
【点睛】本题综合考查了全等三角形的判定与性质、勾股定理及其逆定理、等腰直角三角形等内容,解决本题的关键是能正确分析图形中的相等关系,能在相等的边和角中进行转化,能构造直角三角形进行求解等.
7.A
【分析】本题主要考查勾股定理,理解题意,找出等量关系列出方程是解题关键.设折断处离地面的高度为x尺,根据勾股定理结合题意,列出方程求解即可.
【详解】解:设折断处离地面的高度为x尺,
结合勾股定理可得出:,
解得:.
∴折断处离地面的高度为4.55尺.
故选A.
8.B
【分析】先证明,得到等边,设,则,解得x,在中,计算即可.
【详解】∵等边三角形,,
∴,,
∴,
∴,
∴,
∴,
∵,,
∴,,
设,则,
∵,
解得,
∴,
∴的周长为,
故选B.
【点睛】本题考查了等边三角形的判定和性质,三角形全等的判定和性质,直角三角形的性质,勾股定理,熟练掌握勾股定理,等边三角形的判定,直角三角形的性质是解题的关键.
9.C
【分析】根据题意,画出图形,连接AC,过点C作CE⊥AB于点E,可得CE=BD=8m,在中,由勾股定理,即可求解.
【详解】解:根据题意,画出图形,如下图:连接AC,过点C作CE⊥AB于点E,
根据题意得:AB=8m,CD=2m,BD=8m,AB⊥BD,CD⊥BD,
则四边形BDCE是矩形,
∴CE=BD=8m,
在中,由勾股定理得:
,
即小鸟至少飞行10m.
故选:C.
【点睛】本题主要考查了勾股定理的应用,解题的关键是将现实问题建立数学模型,运用数学知识进行求解.
10.D
【分析】本题考查了勾股定理,根据勾股定理求得,即可求解.
【详解】解:.
故选:D.
11.C
【分析】根据勾股定理求出三边的长度,再判断即可.
【详解】解:由勾股定理得:AC==5,是有理数;
BC==,是无理数;
AB==,是无理数;
即网格上的△ABC三边中,边长为无理数的边数有2条.
故选:C.
【点睛】本题考查了无理数和勾股定理,能正确根据勾股定理求出三边的长度是解此题的关键.
12.A
【分析】根据勾股定理的逆定理可得该三角形为直角三角形,然后再利用三角形的面积公式即可求解.
【详解】∵15 +20 =25 ,
∴此三角形是直角三角形,
∴三角形的面积为=.
故答案为A.
【点睛】本题考查三角形面积公式和勾股定理的逆定理,解题的关键是掌握三角形面积公式和勾股定理的逆定理.
13.5
【分析】如图,构造直角三角形,再利用勾股定理求得斜边.
【详解】如图,做AC⊥BC,在Rt△ABC中,AB==
【点睛】此题主要考查勾股定理的应用.
14.
【分析】首先根据题意可以设DE=EM=x,在三角形AEM中用勾股定理进一步可以用t表示出x,再可以设CF=y,连接MF,所以BF=2 y,在三角形MFN与三角形MFB中利用共用斜边,根据勾股定理可求出用t表示出y,进而根据四边形的面积公式可以求出答案.
【详解】设DE=EM=x,
∴,
∴x=,
设CF=y,连接FM,
∴BF=2 y,
又∵FN= y,NM=1,
∴,
∴y=,
∴四边形的面积为:= 1,
故答案为:.
【点睛】本题主要考查了勾股定理的综合运用,熟练掌握技巧性就可得出答案.
15. 4 或
【分析】先证明点A在第一象限的平分线上,得到,则,再由,利用勾股定理得到,利用因式分解得到,根据两个数的乘积为0,那么两个乘数中至少有一个为0解方程即可.
【详解】解:∵,,,
∴点A在第一象限,点B在x正半轴,
∵OA平分,,
∴点C在y轴正半轴,
∴点A在第一象限的平分线上,
∴,
∴,
∵,
∴,
∴,
∴,
∴或,
∴或,
故答案为:4;或.
【点睛】本题主要考查了坐标与图形,勾股定理,因式分解的应用,正确求出是解题的关键.
16.北偏西18°
【分析】由AC=10海里,AB=8海里,BC=6海里得AC2=AB2+BC2,根据勾股定理的逆定理得到∠ABC=90°,再利用平行线的性质和互余的性质得到∠1,求得∠2.
【详解】解:如图,过点B作BD∥AE,
∵AC=10海里,AB=8海里,BC=6海里,
∴AC2=AB2+BC2,
∴△ABC为直角三角形,即∠ABC=90°,
又∵B点在A的北偏东72°方向,
∴∠1=90°-72°=18°,
∴∠2=∠1=18°,
即快艇位于B的北偏西18°的方向上.
故答案为:北偏西18°.
【点睛】本题考查了利用勾股定理解决航海问题:在每点处画上东南西北,然后利用平行线的性质和勾股定理的逆定理的应用.
17.
【详解】由题意得:小白兔第一次跳12米,第二次跳5米,第三次跳13米;
∵米,
而13 =169,刚好符合直角三角形中勾股定理的逆定理,且第一次和第二次跳的距离为直角边.
故小白兔第一次左拐的角度是90°.
18.0.17米
【分析】根据已知条件,在Rt△ABC中,根据勾股定理求得AC=2米,在Rt△CDE中,根据勾股定理求得CE≈1.83米,即可求得AE=0.17米,即梯子的顶端下滑了0.17米.
【详解】在Rt△ABC中,AB=2.5米,BC=1.5米,
由勾股定理可得AC=2米,
在Rt△ECD中,AB=DE=2.5米,CD=1.5+0.2=1.7米,
由勾股定理可得EC=米,
∴AE=AC-CE=2-1.83=0.17米
答:梯子顶端A下落了约0.17m.
【点睛】本题考查了勾股定理的应用,运用勾股定理求得AC和CE的长是解决问题的关键.
19.
【分析】构造矩形,使得,,在上取一点A使得,,在上取一点B使得,,连接、、得到.然后利用勾股定理证明这个三角形符合条件,再利用分割法求出面积即可.
【详解】解:构造矩形,使得,,在上取一点A使得,,在上取一点B使得,,连接、、得到.
四边形是矩形,
∴,
∴,,
,
∴存在以,,为三条边的三角形.
∴这个三角形的面积为:
.
【点睛】本题考查二次根式的应用、勾股定理、矩形的性质等知识,解题的关键是学会利用数形结合的思想解决问题,属于中考压轴题.
20.
【分析】用正方形的面积减去四个三角形的面积即可.
【详解】S四边形ABCD=5×5-×1×2-×4×2-×3×2-×3×3=25-1-4-3-=.
【点睛】本题考查了求不规则图形的面积,利用整体减局部的方法是解题关键.
21..理由见解析
【分析】本题考查了等边三角形的性质,全等三角形的判定与性质,四边形内角和定理,勾股定理
在四边形中,由四边形内角和定理即可得出结果,以为边向下作等边三角形,有等边三角形的性质得出,证出,证明,得出,证出,再由勾股定理即可得出结论.
【详解】.
理由如下:
如图,以BD为边向下作等边三角形BDQ.
∵,
∴.
∵,,
∴,
∴,.
∵,
∴,
∴.
∵,,
∴.
22.见解析
【分析】利用大图形的面积等于几个小图形的面积和,化简整理即可得到勾股定理表达式.
【详解】证明:如图,连接DB,过点D作BC边上的高DF,则DF=EC=b﹣a,
∵S四边形ADCB=S△ACD+S△ABC=b2+ab,
又∵S四边形ADCB=S△ADB+S△DCB=c2+a(b﹣a),
∴b2+ab=c2+a(b﹣a),
,
即a2+b2=c2.
【点睛】本题考查了勾股定理的证明,用两种方法表示出四边形的面积是解本题的关键.
23.这个零件符合要求
【分析】本题考查勾股定理的逆定理,解题的关键是根据勾股定理的逆定理证明为直角三角形是直角三角形.
【详解】解:连接.
在中,,
所以为直角三角形,,
在中,
所以是直角三角形,,
因此这个零件符合要求.
24.(1)S1+S2=S3
(2)阴影部分的面积为6
【详解】(1)如图,设直角三角形的三边长分别为,则
故答案为:
(2)设直角三角形为S4,直角三角形三边为直径的半圆的面积,,
∵直角边a=3,斜边c=5
∴,则
∴阴影部分的面积S=S1+S2+S4-S3=S4=6
【点睛】本题考查了勾股定理,掌握勾股定理是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
