18.1勾股定理同步练习 沪科版数学八年级下册
文档属性
| 名称 | 18.1勾股定理同步练习 沪科版数学八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
18.1勾股定理
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,一艘船以40km/h的速度沿既定航线由西向东航行,途中接到台风警报,某台风中心正以20km/h的速度由南向北移动,距台风中心200km的圆形区域(包括边界)都属台风影响区,当这艘轮船接到台风警报时,它与台风中心的距离BC=500km,此时台风中心与轮船既定航线的最近距离BA=300km,如果这艘轮船会受到台风影响,那么从接到警报开始,经过( )小时它就会进入台风影响区
A.10 B.7 C.6 D.12
2.公元3世纪切,中国古代书学家赵爽注《周髀算经》时,创适了“赵爽弦图”如图.勾a=3,弦c=5,则小正方形ABCD的面积为( )
A.1 B.3 C.4 D.9
3.如图,以直角三角形的三边为边,分别向外作等边三角形、半圆、等腰直角三角形和正方形,上述四种情况的面积关系满足S1+S2=S3的图形有( )
A.1个 B.2个 C.3个 D.4个
4.一个直角三角形的两条直角边长分别为6 cm和8 cm,那么这个直角三角形的斜边长为( )
A.6 cm B.8 cm C.10 cm D.24 cm
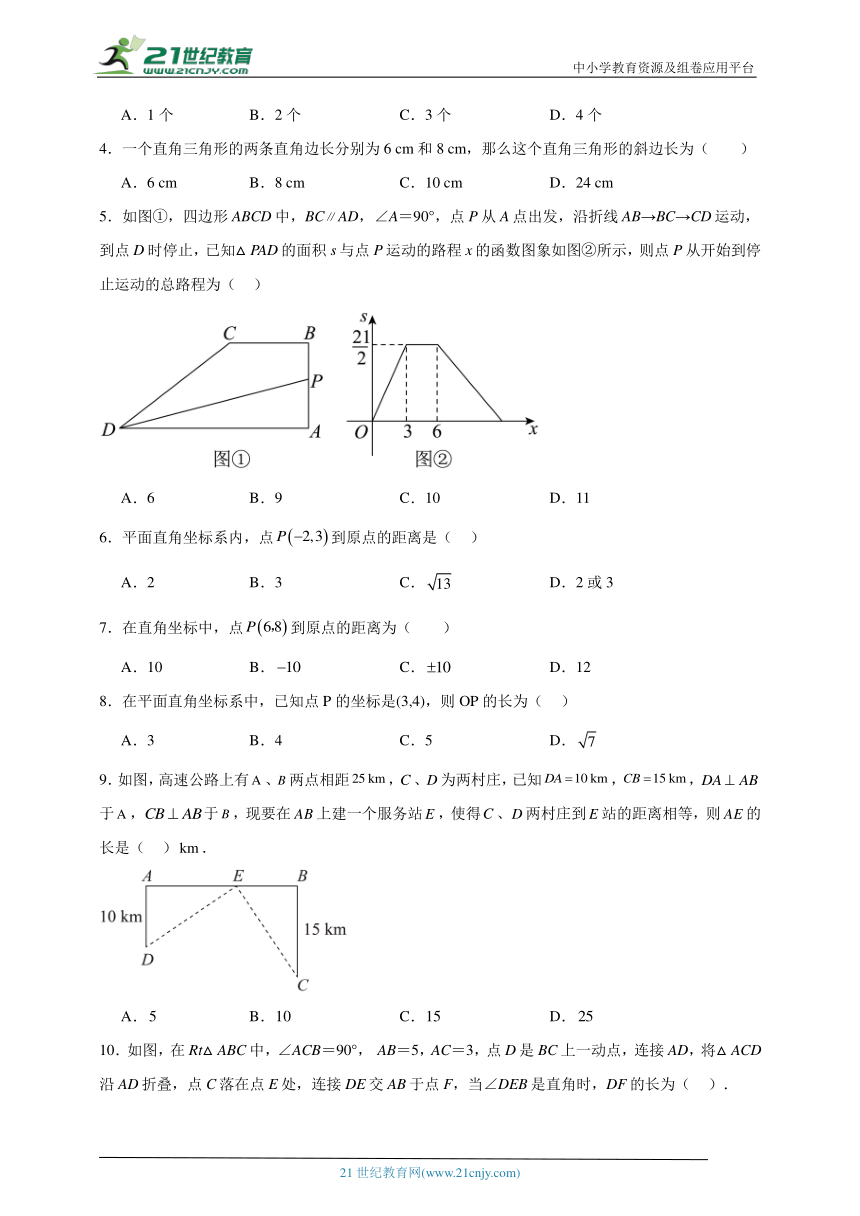
5.如图①,四边形ABCD中,BCAD,∠A=90°,点P从A点出发,沿折线AB→BC→CD运动,到点D时停止,已知△PAD的面积s与点P运动的路程x的函数图象如图②所示,则点P从开始到停止运动的总路程为( )
A.6 B.9 C.10 D.11
6.平面直角坐标系内,点到原点的距离是( )
A.2 B.3 C. D.2或3
7.在直角坐标中,点到原点的距离为( )
A.10 B. C. D.12
8.在平面直角坐标系中,已知点P的坐标是(3,4),则OP的长为( )
A.3 B.4 C.5 D.
9.如图,高速公路上有、两点相距,、为两村庄,已知,,于,于,现要在上建一个服务站,使得、两村庄到站的距离相等,则的长是( ).
A. B. C. D.
10.如图,在Rt△ABC中,∠ACB=90°, AB=5,AC=3,点D是BC上一动点,连接AD,将△ACD沿AD折叠,点C落在点E处,连接DE交AB于点F,当∠DEB是直角时,DF的长为( ).
A.5 B.3 C. D.
11.如图,我国古代的“赵爽弦图”是由四个全等的直角三角形和一个小正方形密铺构成的大正方形,若小正方形的面积为1,大正方形的面积为13,则直角三角形较短的直角边a与较长的直角边b的比的值是( )
A. B. C. D.
12.如图,有两棵树高分别为6米、2米,它们相距5米,一只小鸟从一棵树的树梢飞到另一棵树的树梢,一共飞了多少米?( )
A.41 B. C.3 D.9
二、填空题
13.已知圆锥的高是,圆锥的底面半径是,则该圆锥的侧面积是 .
14.利用数形结合的思想,可以比较实数的大小.若在方格纸中构造如图所示的图形(方格纸中每个小方格的边长为1),结合图形可得 .(填“”“”或“”)
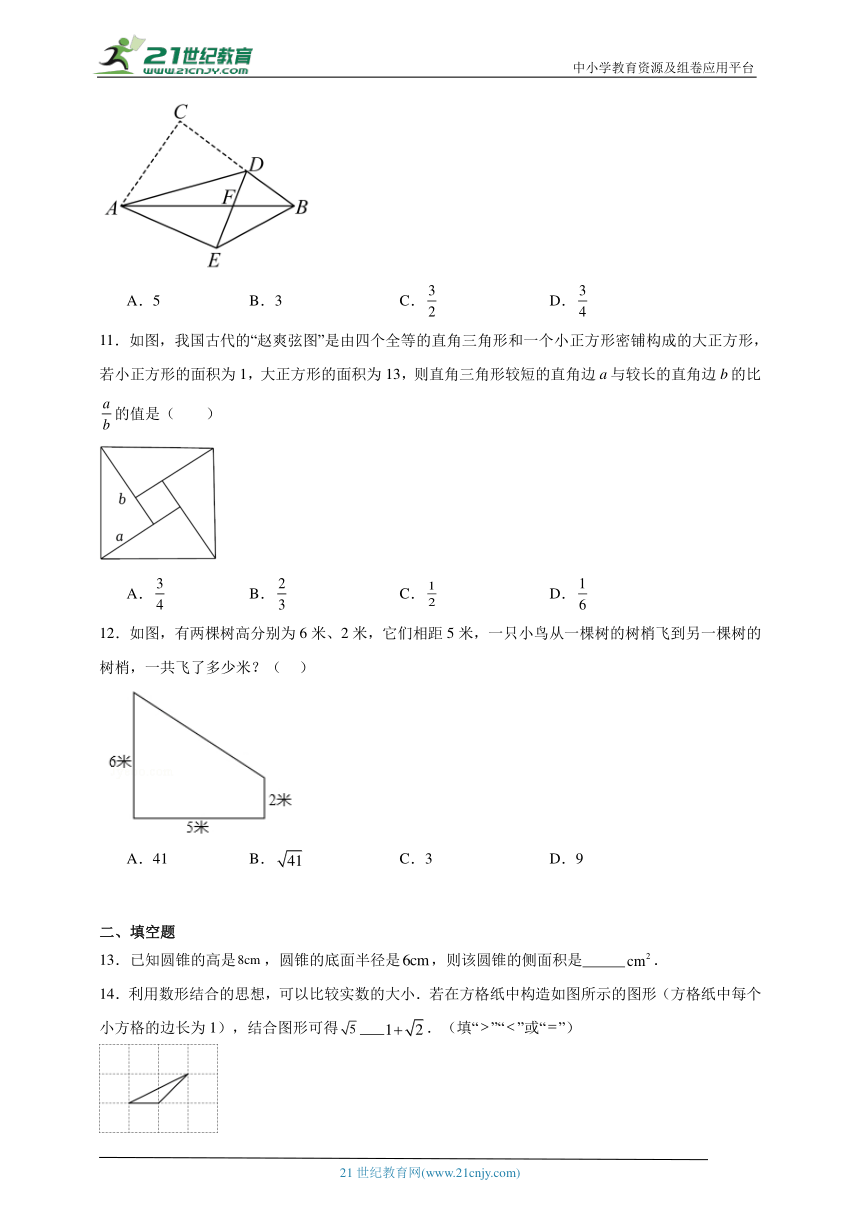
15.在Rt△ABC中,∠B=90°,AB=3,BC=4,点E是△ABC内一点,点D是BC的中点,连接DE、AE,且DE=DB,点F是DE的中点,则AE+CF的最小值是 .(提示:连接CE,等腰三角形两腰上的中线相等)
16.在△ABC中,∠ACB=90°,AB=5 cm,AC= 3 cm,CD⊥AB于点D,则CD的长为 .
17.如图,,点,分别在边,上,且,,点,分别在边,上,则的最小值是 .
三、解答题
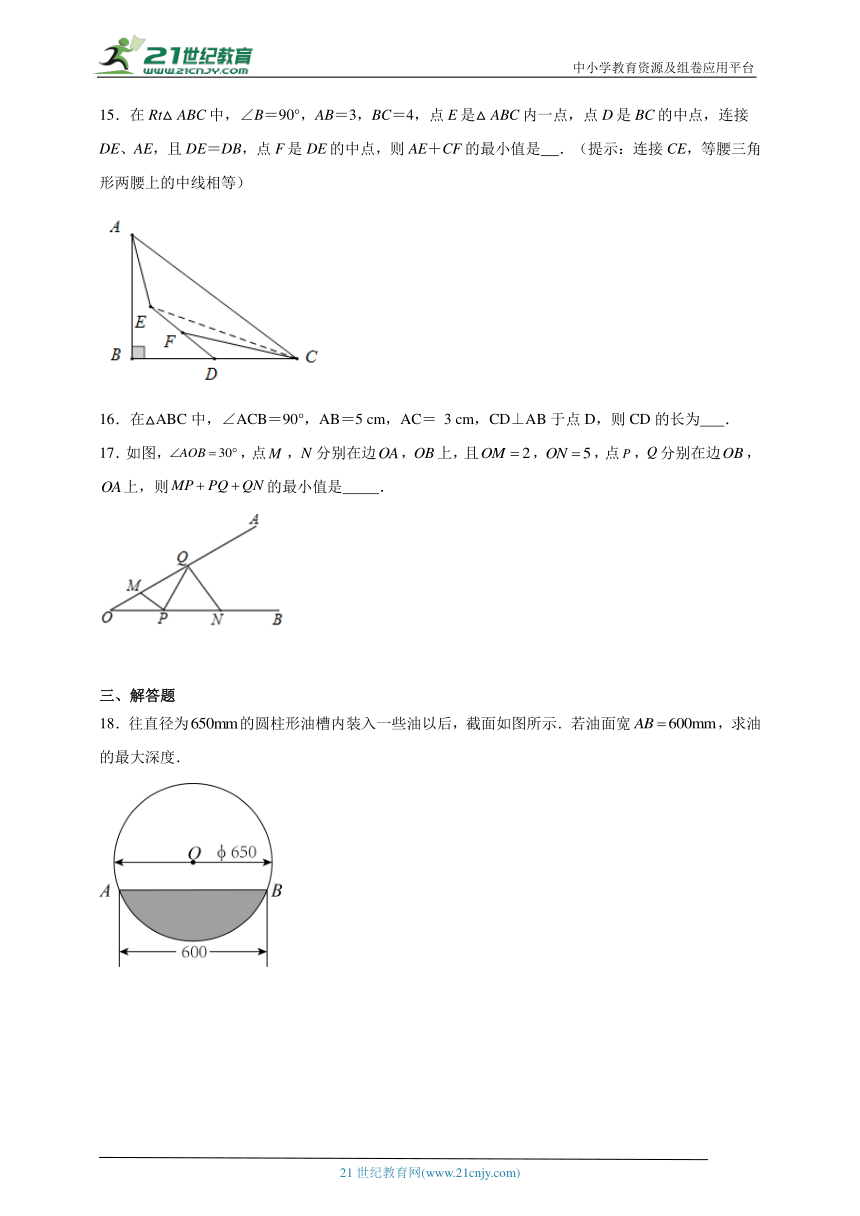
18.往直径为的圆柱形油槽内装入一些油以后,截面如图所示.若油面宽,求油的最大深度.
19.如图,在△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线,CD=5cm,求AB的长.
20.已知△ABC为等边三角形,点D为直线BC上的一动点(点D不与B、C重合),以AD为边作菱形ADEF(A、D、E、F按逆时针排列),使∠DAF=60°,连接CF.
(1)如图1,当点D在边BC上时,求证:①BD=CF;②AC=CF+CD;
(2)如图2,当点D在边BC的延长线上且其他条件不变时,结论AC=CF+CD是否成立?若不成立,请写出AC、CF、CD之间存在的数量关系,并说明理由;
(3)如图3,当点D在边BC的延长线上且其他条件不变时,补全图形,并直接写出AC、CF、CD之间存在的数量关系
21.如图,一架长为5米的梯子AB斜靠在与地面OM垂直的墙ON上,梯子底端距离墙ON有3米.
(1)求梯子顶端与地面的距离OA的长.
(2)若梯子顶点A下滑1米到C点,求梯子的底端向右滑到D的距离.
22.在中,,D是的中点,以为腰向外作等腰直角连接,交于点F,交于点G.
(1)求证:;
(2)试判断线段与三者之间的等量关系,并证明你的结论.
23.在中,,垂足为D,求的长.
24.嘉嘉参加机器人设计活动,需操控机器人在5×5的方格棋盘上从A点行走至B点,且每个小方格皆为正方形,主办单位规定了三条行走路径R1,R2,R3,其行经位置如图与表所示:
路径 编号 图例 行径位置
第一条路径 R1 _ A→C→D→B
第二条路径 R2 … A→E→D→F→B
第三条路径 R3 ▂ A→G→B
已知A、B、C、D、E、F、G七点皆落在格线的交点上,且两点之间的路径皆为直线,在无法使用任何工具测量的条件下,请判断R1、R2、R3这三条路径中,最长与最短的路径分别为何?请写出你的答案,并完整说明理由.
《18.1勾股定理》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B A D C D C A C C C
题号 11 12
答案 B B
1.B
【分析】首先根据题意结合题目条件画出图形,进而利用勾股定理得出等式计算即可.
【详解】解:由题意,作图如下:
设x小时后,就进入台风影响区,根据题意得出:
CE=40x千米,BB′=20x千米,
∵BC=500km,AB=300km,
∴AC=400km,
∴AE=400-40x,AB′=300-20x,
∴AE2+AB′2=EB′2,
即(400-40x)2+(300-20x)2=2002,
解得:x1=,x2=(不符合题意,舍去).
故答案为:B.
【点睛】此题主要考查了一元二次方程的应用以及勾股定理等知识,根据题意得出关于x的等式是解题关键.
2.A
【分析】应用勾股定理和正方形的面积公式可求解.
【详解】∵勾a=3,弦c=5,
∴股b= ,
∴小正方形的边长=4 3=1,
∴小正方形的面积=1×1=1
故选:A.
【点睛】本题运用了勾股定理和正方形的面积公式,关键是运用了数形结合的数学思想.
3.D
【详解】解:(1)S1=,S2=,S3=,∵,∴,∴S1+S2=S3.
(2)S1=,S2=,S3=,∵,∴,∴S1+S2=S3.
(3)S1=,S2=,S3=,∵,∴,∴S1+S2=S3.
(4)S1=,S2=,S3=,∵,∴S1+S2=S3.
综上,可得:面积关系满足S1+S2=S3图形有4个.
故选D.
4.C
【详解】根据勾股定理可以得出:斜边长==10cm.
故选:C.
点睛:此题主要考查了勾股定理的应用,关键是灵活应用勾股定理的公式计算.
5.D
【分析】过点C作CE⊥AD于点E,根据函数图象,得出AB、BC和三角形ADB的面积,从而可以求得AD的长,再根据题意,得出四边形ABCE是长方形,再根据长方形的定义,得出、的长,再根据勾股定理,得出的长,进而求得点P从开始到停止运动的总路程.
【详解】解:如图,过点C作CE⊥AD于点E,
由图②可知,点P从A到B运动的路程是3,即;当点P与点B重合时,△ADP的面积是,由B到C运动的路程为3,即,
∴,
解得:,
又∵,,,
∴,,
∴四边形ABCE是长方形,
∴,,
∴,
∴,
∴点P从开始到停止运动的总路程为:.
故选:D
【点睛】本题考查了根据函数图象获取信息、动点问题的函数图象、勾股定理,解本题的关键在理解题意,能从函数图象中找到准确的信息,利用数形结合思想进行解答.
6.C
【分析】利用勾股定理计算判断.
【详解】∵点,
∴点到原点的距离是=,
故选C.
【点睛】本题考查了点到原点的距离,熟练运用勾股定理是解题的关键.
7.A
【分析】点的横纵坐标的绝对值和这点到原点的距离组成一个直角三角形,利用勾股定理求解即可.
【详解】解:点到原点的距离为: ,
故选A.
【点睛】本题考查了两点间的距离公式,用到的知识点为:点到原点的距离是此点的横纵坐标的绝对值为两直角边的直角三角形的斜边.
8.C
【分析】画图,根据勾股定理求解.
【详解】如图所示:
∵P(3,4),
∴OP==5.
故选C.
【点睛】本题考查的是勾股定理及坐标与图形性质,根据题意画出图形,利用数形结合求解是解答此题的关键.
9.C
【分析】根据题意设出的长为,再由勾股定理列出方程求解即可.
【详解】解:设,则,
由勾股定理得:
在中,
,
在中,
,
由题意可知:,
所以:,
解得:.
所以,应建在距点处.
故选:.
【点睛】本题考查正确运用勾股定理,善于观察题目的信息是解题以及学好数学的关键.
10.C
【分析】如图,由题意知,,,,可知三点共线,与重合,在中,由勾股定理得,求的值,设,,在中,由勾股定理得,计算求解即可.
【详解】解:如图,
∵是直角
∴
由题意知,,
∴
∴三点共线
∴与重合
在中,由勾股定理得
设,
在中,由勾股定理得即
解得
∴的长为
故选C.
【点睛】本题考查了折叠的性质,勾股定理等知识.解题的关键在于明确三点共线,与重合.
11.B
【分析】根据勾股定理可以求得等于大正方形的面积,然后求四个直角三角形的面积,即可得到2ab的值,然后根据即可求得(a+b)的值;根据小正方形的面积为即可求得,进而联立方程组求得a与b的值,则可求出答案.
【详解】解:∵大正方形的面积是13,设边长为c,
∴,
∴,
∵直角三角形的面积是,
又∵直角三角形的面积是,
∴,
∴,
∴.
∵小正方形的面积为,
又∵,
∴,
联立可得 ,解得 ,
∴.
故选:B.
【点睛】本题考查了勾股定理以及完全平方公式的知识,解题关键是熟记完全平方公式,还要注意图形的面积和a、b之间的关系.
12.B
【详解】解:如图所示,作DE⊥AB交AB与E点,则四边形CDEB为矩形,三角形AED为直角三角形.∵AB=6,BC=5,CD=2,∴BE=2,DE=5,∴AE=AB﹣BE=4,在直角三角形AED中,由勾股定理可得:AD2=AE2+ED2,∴AD==.故选B.
点睛:本题考查了矩形的性质及运用勾股定理解直角三角形.
13.
【分析】本题考查了圆锥的侧面积的计算方法,解决本题的关键是根据已知条件求出圆锥的母线长和侧面展开扇形的弧长,然后用弧长与母线长乘积的一半求扇形的面积.根据圆锥的底面半径和高求出圆锥的母线长,再根据圆锥的底面周长等于圆锥的侧面展开扇形的弧长,最后利用扇形的面积计算方法求得侧面积.
【详解】解:由勾股定理得:圆锥的母线长,
∵圆锥的底面周长为,
∴圆锥的侧面展开扇形的弧长为,
∴圆锥的侧面积为:.
故答案为:.
14.
【分析】本题考查勾股定理与网格问题,比较实数的大小关系,三角形的三边关系,解题的关键是掌握以上知识点.
根据勾股定理得出三角形的三边长,再利用三角形的三边关系即可得出结果;
【详解】解:根据图象得,画出的三角形的三边长分别为:,
根据三角形的三边关系可得:,
故答案为:.
15.
【分析】取CD的中点G,根据等腰三角形两腰上的中线相等得到AE+CF= AE+EGAG,当点A、E、G共线时,AE+CF有最小值,最小值为线段AG的长,利用勾股定理即可求解.
【详解】解:取CD的中点G,连接CE、EG、AG,
∵点D是BC的中点,且DE=DB,
∴DE=DC,即△DEC是等腰三角形,
∵点CF、EG是等腰三角形△DEC两腰上的中线,
∴DG=DF=ED=CD,
在△DEG和△DCF中,,
∴CF=EG,
∴AE+CF= AE+EGAG,
∴当点A、E、G共线时,AE+CF有最小值,最小值为线段AG的长,
∵点D是BC的中点,点G是DC的中点,且BC=4,
∴BG=3,
又AB=3,且∠B=90°,
AG=.
故答案为:.
【点睛】本题考查了等腰三角形的性质,勾股定理,得到当点A、E、G共线时,AE+CF有最小值,最小值为线段AG的长是解题的关键.
16.2.4cm
【详解】如图,∵在△ABC中,∠ACB=90°,AB=5 cm,AC= 3 cm,
∴BC=,
∵CD⊥AB于点D,
∴S△ABC=AB·CD=AC·BC=6,
即;CD=6,解得:CD=2.4(cm).
故答案为2.4cm.
点睛:本题的解题要点是:首先在Rt△ABC中,由勾股定理求得BC的长,再结合“直角三角形的面积既等于两直角边乘积的一半,也等于斜边和斜边上的高的乘积的一半”列出关于CD的方程,就可使问题得到解决.
17.
【分析】作关于的对称点,作关于的对称点,连接,即为的最小值;证出为等边三角形,为等边三角形,得出,由勾股定理求出即可.
【详解】解:作关于的对称点,作关于的对称点,连接,如图所示:
连接,即为的最小值.
根据轴对称的定义可知:,,
为等边三角形,为等边三角形,
,,,
在中,
.
故答案为:.
【点睛】本题考查了轴对称--最短路径问题,根据轴对称的性质,找到相等的线段,得到等边三角形是解题的关键.
18.200mm
【分析】先过点O作OD⊥AB于点D,交于点F,连接OA,由垂径定理可求出AD的长,再根据勾股定理求出OD的长,进而可得出DF的长.
【详解】解:过点O作OD⊥AB于点D,交于点F,连接OA,
∵AB=600mm,
∴AD==300mm,
∵直径为650mm,
∴OA=×650=325mm,
∴OD===125mm,
∴DF=OF OD=×650 125=200mm.
答:油的最大深度为200mm.
【点睛】本题考查的是垂径定理的应用及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
19.10cm
【分析】先有∠A=30°,那么∠ABC=60°,结合BD是角平分线,那么可求出∠DBC=∠ABD=30°,在Rt△DBC中,利用直角三角形中30°的角所对的直角边等于斜边的一半,可求出BD,再利用勾股定理可求BC,同理,在Rt△ABC中,AB=2BC,即可求AB.
【详解】解:在Rt△ABC中,∠C=90°,∠A=∠30°,
∴∠ABC=60°.
∵BD是∠ABC的平分线,
∴∠ABD=∠CBD=30°.
∴∠ABD=∠BAD,
∴AD=DB,
在Rt△CBD中,CD=5cm,∠CBD=30°,
∴BD=10cm.
由勾股定理得,BC=5,
∴AB=2BC=10(cm).
【点睛】本题利用了角平分线定义、直角三角形中30°的角所对的直角边等于斜边的一半、勾股定理等知识.
20.(1)见解析;
(2)见解析;
(3)见解析.
【分析】(1)根据已知得出AF=AD,AB=BC=AC,∠BAC=∠DAF=60°,求出∠BAD=CAF,由SAS证△BAD≌△CAF,推出CF=BD即可.
(2)求出∠BAD=∠CAF,根据SAS证△BAD≌△CAF,推出BD=CF即可.
(3)画出图形后,根据SAS证△BAD≌△CAF,推出CF=BD即可:
【详解】解:(1)证明:∵四边形AFED是菱形,
∴AF=AD
∵△ABC是等边三角形,
∴AB=AC=BC,∠BAC=60°=∠DAF
∴∠BAC-∠DAC=∠DAF-∠DAC,即∠BAD=∠CAF
∵在△BAD和△CAF中, AB=AC,∠BAD=∠CAF,AD=AF,
∴△BAD≌△CAF(SAS)
∴CF=BD
∴CF+CD=BD+CD=BC=AC.
即①BD=CF,②AC=CF+CD.
(2)AC=CF+CD不成立,AC、CF、CD之间存在的数量关系是AC=CF-CD.理由如下:
由(1)知:AB=AC=BC,AD=AF,∠BAC=∠DAF=60°,
∴∠BAC+∠DAC=∠DAF+∠DAC,即∠BAD=∠CAF
∵在△BAD和△CAF中,AC=AB,∠BAD=∠CAF ,AD=AF,
∴△BAD≌△CAF(SAS)
∴BD=CF
∴CF-CD=BD-CD=BC=AC,即AC=CF-CD.
(3)补全图形如下,AC、CF、CD之间的数量关系为AC=CD-CF.
∵∠BAC=∠DAF=60°,
∴∠DAB=∠CAF,
∵在△BAD和△CAF中, AB=AC,∠DAB=∠CAF, AD=AF,
∴△BAD≌△CAF(SAS).
∴CF=BD.
∴CD-CF=CD-BD=BC=AC.
21.(1)4米
(2)1米
【分析】(1)根据勾股定理直接求出OA的长度即可;
(2)先求出OC的长度,然后根据勾股定理求出OD的长度,用OD-OB即可得出答案.
【详解】(1)解:∵∠AOB=90°,米,米,
∴AO==4(米),
答:梯子顶端与地面的距离OA的长为4米.
(2)解:∵(米),米,
∴OD==4(米),
∴BD=OD﹣OB=4﹣3=1(米).
【点睛】本题主要考查了勾股定理的应用,解题的关键是熟练掌握勾股定理的内容,如果一个直角三角形的两条直角边为a、b,斜边为c,那么.
22.(1)见解析
(2),理由见解析
【分析】本题考查了等腰三角形的性质、全等三角形综合问题以及勾股定理,证是解题关键.
(1)证得,结合、可得,即可求证;
(2)由得,结合,得,根据勾股定理即可求解.
【详解】(1)证明:∵,D是的中点,
∴,
∵,
∴,
∴,
由题意得:,
∴,
∴,
∴;
(2)解:,理由如下:
∵,
∴,
∵,,
∴,
∴,
∵,
∴.
23.
【分析】此题考查了勾股定理,以及三角形面积求法,熟练掌握勾股定理是解本题的关键.
用勾股定理求的长,再利用面积求,在中,用勾股定理求.
【详解】
解:在中,,
,
.
由三角形的面积公式得,
∴.
在中,,
.
.
所以的长为.
24.最长路径为A→E→D→F→B;最短路径为A→G→B,理由见解析.
【分析】利用勾股定理分别计算出三条路径的长,比较大小即可得.
【详解】第一条路径的长度为++=2+,
第二条路径的长度为++1+=+++1,
第三条路径的长度为+=2+,
∵2+<2+<+++1,
∴最长路径为A→E→D→F→B;最短路径为A→G→B.
【点睛】本题主要考查勾股定理的应用,解题的关键是根据勾股定理求得每条线段的长度.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
18.1勾股定理
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,一艘船以40km/h的速度沿既定航线由西向东航行,途中接到台风警报,某台风中心正以20km/h的速度由南向北移动,距台风中心200km的圆形区域(包括边界)都属台风影响区,当这艘轮船接到台风警报时,它与台风中心的距离BC=500km,此时台风中心与轮船既定航线的最近距离BA=300km,如果这艘轮船会受到台风影响,那么从接到警报开始,经过( )小时它就会进入台风影响区
A.10 B.7 C.6 D.12
2.公元3世纪切,中国古代书学家赵爽注《周髀算经》时,创适了“赵爽弦图”如图.勾a=3,弦c=5,则小正方形ABCD的面积为( )
A.1 B.3 C.4 D.9
3.如图,以直角三角形的三边为边,分别向外作等边三角形、半圆、等腰直角三角形和正方形,上述四种情况的面积关系满足S1+S2=S3的图形有( )
A.1个 B.2个 C.3个 D.4个
4.一个直角三角形的两条直角边长分别为6 cm和8 cm,那么这个直角三角形的斜边长为( )
A.6 cm B.8 cm C.10 cm D.24 cm
5.如图①,四边形ABCD中,BCAD,∠A=90°,点P从A点出发,沿折线AB→BC→CD运动,到点D时停止,已知△PAD的面积s与点P运动的路程x的函数图象如图②所示,则点P从开始到停止运动的总路程为( )
A.6 B.9 C.10 D.11
6.平面直角坐标系内,点到原点的距离是( )
A.2 B.3 C. D.2或3
7.在直角坐标中,点到原点的距离为( )
A.10 B. C. D.12
8.在平面直角坐标系中,已知点P的坐标是(3,4),则OP的长为( )
A.3 B.4 C.5 D.
9.如图,高速公路上有、两点相距,、为两村庄,已知,,于,于,现要在上建一个服务站,使得、两村庄到站的距离相等,则的长是( ).
A. B. C. D.
10.如图,在Rt△ABC中,∠ACB=90°, AB=5,AC=3,点D是BC上一动点,连接AD,将△ACD沿AD折叠,点C落在点E处,连接DE交AB于点F,当∠DEB是直角时,DF的长为( ).
A.5 B.3 C. D.
11.如图,我国古代的“赵爽弦图”是由四个全等的直角三角形和一个小正方形密铺构成的大正方形,若小正方形的面积为1,大正方形的面积为13,则直角三角形较短的直角边a与较长的直角边b的比的值是( )
A. B. C. D.
12.如图,有两棵树高分别为6米、2米,它们相距5米,一只小鸟从一棵树的树梢飞到另一棵树的树梢,一共飞了多少米?( )
A.41 B. C.3 D.9
二、填空题
13.已知圆锥的高是,圆锥的底面半径是,则该圆锥的侧面积是 .
14.利用数形结合的思想,可以比较实数的大小.若在方格纸中构造如图所示的图形(方格纸中每个小方格的边长为1),结合图形可得 .(填“”“”或“”)
15.在Rt△ABC中,∠B=90°,AB=3,BC=4,点E是△ABC内一点,点D是BC的中点,连接DE、AE,且DE=DB,点F是DE的中点,则AE+CF的最小值是 .(提示:连接CE,等腰三角形两腰上的中线相等)
16.在△ABC中,∠ACB=90°,AB=5 cm,AC= 3 cm,CD⊥AB于点D,则CD的长为 .
17.如图,,点,分别在边,上,且,,点,分别在边,上,则的最小值是 .
三、解答题
18.往直径为的圆柱形油槽内装入一些油以后,截面如图所示.若油面宽,求油的最大深度.
19.如图,在△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线,CD=5cm,求AB的长.
20.已知△ABC为等边三角形,点D为直线BC上的一动点(点D不与B、C重合),以AD为边作菱形ADEF(A、D、E、F按逆时针排列),使∠DAF=60°,连接CF.
(1)如图1,当点D在边BC上时,求证:①BD=CF;②AC=CF+CD;
(2)如图2,当点D在边BC的延长线上且其他条件不变时,结论AC=CF+CD是否成立?若不成立,请写出AC、CF、CD之间存在的数量关系,并说明理由;
(3)如图3,当点D在边BC的延长线上且其他条件不变时,补全图形,并直接写出AC、CF、CD之间存在的数量关系
21.如图,一架长为5米的梯子AB斜靠在与地面OM垂直的墙ON上,梯子底端距离墙ON有3米.
(1)求梯子顶端与地面的距离OA的长.
(2)若梯子顶点A下滑1米到C点,求梯子的底端向右滑到D的距离.
22.在中,,D是的中点,以为腰向外作等腰直角连接,交于点F,交于点G.
(1)求证:;
(2)试判断线段与三者之间的等量关系,并证明你的结论.
23.在中,,垂足为D,求的长.
24.嘉嘉参加机器人设计活动,需操控机器人在5×5的方格棋盘上从A点行走至B点,且每个小方格皆为正方形,主办单位规定了三条行走路径R1,R2,R3,其行经位置如图与表所示:
路径 编号 图例 行径位置
第一条路径 R1 _ A→C→D→B
第二条路径 R2 … A→E→D→F→B
第三条路径 R3 ▂ A→G→B
已知A、B、C、D、E、F、G七点皆落在格线的交点上,且两点之间的路径皆为直线,在无法使用任何工具测量的条件下,请判断R1、R2、R3这三条路径中,最长与最短的路径分别为何?请写出你的答案,并完整说明理由.
《18.1勾股定理》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B A D C D C A C C C
题号 11 12
答案 B B
1.B
【分析】首先根据题意结合题目条件画出图形,进而利用勾股定理得出等式计算即可.
【详解】解:由题意,作图如下:
设x小时后,就进入台风影响区,根据题意得出:
CE=40x千米,BB′=20x千米,
∵BC=500km,AB=300km,
∴AC=400km,
∴AE=400-40x,AB′=300-20x,
∴AE2+AB′2=EB′2,
即(400-40x)2+(300-20x)2=2002,
解得:x1=,x2=(不符合题意,舍去).
故答案为:B.
【点睛】此题主要考查了一元二次方程的应用以及勾股定理等知识,根据题意得出关于x的等式是解题关键.
2.A
【分析】应用勾股定理和正方形的面积公式可求解.
【详解】∵勾a=3,弦c=5,
∴股b= ,
∴小正方形的边长=4 3=1,
∴小正方形的面积=1×1=1
故选:A.
【点睛】本题运用了勾股定理和正方形的面积公式,关键是运用了数形结合的数学思想.
3.D
【详解】解:(1)S1=,S2=,S3=,∵,∴,∴S1+S2=S3.
(2)S1=,S2=,S3=,∵,∴,∴S1+S2=S3.
(3)S1=,S2=,S3=,∵,∴,∴S1+S2=S3.
(4)S1=,S2=,S3=,∵,∴S1+S2=S3.
综上,可得:面积关系满足S1+S2=S3图形有4个.
故选D.
4.C
【详解】根据勾股定理可以得出:斜边长==10cm.
故选:C.
点睛:此题主要考查了勾股定理的应用,关键是灵活应用勾股定理的公式计算.
5.D
【分析】过点C作CE⊥AD于点E,根据函数图象,得出AB、BC和三角形ADB的面积,从而可以求得AD的长,再根据题意,得出四边形ABCE是长方形,再根据长方形的定义,得出、的长,再根据勾股定理,得出的长,进而求得点P从开始到停止运动的总路程.
【详解】解:如图,过点C作CE⊥AD于点E,
由图②可知,点P从A到B运动的路程是3,即;当点P与点B重合时,△ADP的面积是,由B到C运动的路程为3,即,
∴,
解得:,
又∵,,,
∴,,
∴四边形ABCE是长方形,
∴,,
∴,
∴,
∴点P从开始到停止运动的总路程为:.
故选:D
【点睛】本题考查了根据函数图象获取信息、动点问题的函数图象、勾股定理,解本题的关键在理解题意,能从函数图象中找到准确的信息,利用数形结合思想进行解答.
6.C
【分析】利用勾股定理计算判断.
【详解】∵点,
∴点到原点的距离是=,
故选C.
【点睛】本题考查了点到原点的距离,熟练运用勾股定理是解题的关键.
7.A
【分析】点的横纵坐标的绝对值和这点到原点的距离组成一个直角三角形,利用勾股定理求解即可.
【详解】解:点到原点的距离为: ,
故选A.
【点睛】本题考查了两点间的距离公式,用到的知识点为:点到原点的距离是此点的横纵坐标的绝对值为两直角边的直角三角形的斜边.
8.C
【分析】画图,根据勾股定理求解.
【详解】如图所示:
∵P(3,4),
∴OP==5.
故选C.
【点睛】本题考查的是勾股定理及坐标与图形性质,根据题意画出图形,利用数形结合求解是解答此题的关键.
9.C
【分析】根据题意设出的长为,再由勾股定理列出方程求解即可.
【详解】解:设,则,
由勾股定理得:
在中,
,
在中,
,
由题意可知:,
所以:,
解得:.
所以,应建在距点处.
故选:.
【点睛】本题考查正确运用勾股定理,善于观察题目的信息是解题以及学好数学的关键.
10.C
【分析】如图,由题意知,,,,可知三点共线,与重合,在中,由勾股定理得,求的值,设,,在中,由勾股定理得,计算求解即可.
【详解】解:如图,
∵是直角
∴
由题意知,,
∴
∴三点共线
∴与重合
在中,由勾股定理得
设,
在中,由勾股定理得即
解得
∴的长为
故选C.
【点睛】本题考查了折叠的性质,勾股定理等知识.解题的关键在于明确三点共线,与重合.
11.B
【分析】根据勾股定理可以求得等于大正方形的面积,然后求四个直角三角形的面积,即可得到2ab的值,然后根据即可求得(a+b)的值;根据小正方形的面积为即可求得,进而联立方程组求得a与b的值,则可求出答案.
【详解】解:∵大正方形的面积是13,设边长为c,
∴,
∴,
∵直角三角形的面积是,
又∵直角三角形的面积是,
∴,
∴,
∴.
∵小正方形的面积为,
又∵,
∴,
联立可得 ,解得 ,
∴.
故选:B.
【点睛】本题考查了勾股定理以及完全平方公式的知识,解题关键是熟记完全平方公式,还要注意图形的面积和a、b之间的关系.
12.B
【详解】解:如图所示,作DE⊥AB交AB与E点,则四边形CDEB为矩形,三角形AED为直角三角形.∵AB=6,BC=5,CD=2,∴BE=2,DE=5,∴AE=AB﹣BE=4,在直角三角形AED中,由勾股定理可得:AD2=AE2+ED2,∴AD==.故选B.
点睛:本题考查了矩形的性质及运用勾股定理解直角三角形.
13.
【分析】本题考查了圆锥的侧面积的计算方法,解决本题的关键是根据已知条件求出圆锥的母线长和侧面展开扇形的弧长,然后用弧长与母线长乘积的一半求扇形的面积.根据圆锥的底面半径和高求出圆锥的母线长,再根据圆锥的底面周长等于圆锥的侧面展开扇形的弧长,最后利用扇形的面积计算方法求得侧面积.
【详解】解:由勾股定理得:圆锥的母线长,
∵圆锥的底面周长为,
∴圆锥的侧面展开扇形的弧长为,
∴圆锥的侧面积为:.
故答案为:.
14.
【分析】本题考查勾股定理与网格问题,比较实数的大小关系,三角形的三边关系,解题的关键是掌握以上知识点.
根据勾股定理得出三角形的三边长,再利用三角形的三边关系即可得出结果;
【详解】解:根据图象得,画出的三角形的三边长分别为:,
根据三角形的三边关系可得:,
故答案为:.
15.
【分析】取CD的中点G,根据等腰三角形两腰上的中线相等得到AE+CF= AE+EGAG,当点A、E、G共线时,AE+CF有最小值,最小值为线段AG的长,利用勾股定理即可求解.
【详解】解:取CD的中点G,连接CE、EG、AG,
∵点D是BC的中点,且DE=DB,
∴DE=DC,即△DEC是等腰三角形,
∵点CF、EG是等腰三角形△DEC两腰上的中线,
∴DG=DF=ED=CD,
在△DEG和△DCF中,,
∴CF=EG,
∴AE+CF= AE+EGAG,
∴当点A、E、G共线时,AE+CF有最小值,最小值为线段AG的长,
∵点D是BC的中点,点G是DC的中点,且BC=4,
∴BG=3,
又AB=3,且∠B=90°,
AG=.
故答案为:.
【点睛】本题考查了等腰三角形的性质,勾股定理,得到当点A、E、G共线时,AE+CF有最小值,最小值为线段AG的长是解题的关键.
16.2.4cm
【详解】如图,∵在△ABC中,∠ACB=90°,AB=5 cm,AC= 3 cm,
∴BC=,
∵CD⊥AB于点D,
∴S△ABC=AB·CD=AC·BC=6,
即;CD=6,解得:CD=2.4(cm).
故答案为2.4cm.
点睛:本题的解题要点是:首先在Rt△ABC中,由勾股定理求得BC的长,再结合“直角三角形的面积既等于两直角边乘积的一半,也等于斜边和斜边上的高的乘积的一半”列出关于CD的方程,就可使问题得到解决.
17.
【分析】作关于的对称点,作关于的对称点,连接,即为的最小值;证出为等边三角形,为等边三角形,得出,由勾股定理求出即可.
【详解】解:作关于的对称点,作关于的对称点,连接,如图所示:
连接,即为的最小值.
根据轴对称的定义可知:,,
为等边三角形,为等边三角形,
,,,
在中,
.
故答案为:.
【点睛】本题考查了轴对称--最短路径问题,根据轴对称的性质,找到相等的线段,得到等边三角形是解题的关键.
18.200mm
【分析】先过点O作OD⊥AB于点D,交于点F,连接OA,由垂径定理可求出AD的长,再根据勾股定理求出OD的长,进而可得出DF的长.
【详解】解:过点O作OD⊥AB于点D,交于点F,连接OA,
∵AB=600mm,
∴AD==300mm,
∵直径为650mm,
∴OA=×650=325mm,
∴OD===125mm,
∴DF=OF OD=×650 125=200mm.
答:油的最大深度为200mm.
【点睛】本题考查的是垂径定理的应用及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
19.10cm
【分析】先有∠A=30°,那么∠ABC=60°,结合BD是角平分线,那么可求出∠DBC=∠ABD=30°,在Rt△DBC中,利用直角三角形中30°的角所对的直角边等于斜边的一半,可求出BD,再利用勾股定理可求BC,同理,在Rt△ABC中,AB=2BC,即可求AB.
【详解】解:在Rt△ABC中,∠C=90°,∠A=∠30°,
∴∠ABC=60°.
∵BD是∠ABC的平分线,
∴∠ABD=∠CBD=30°.
∴∠ABD=∠BAD,
∴AD=DB,
在Rt△CBD中,CD=5cm,∠CBD=30°,
∴BD=10cm.
由勾股定理得,BC=5,
∴AB=2BC=10(cm).
【点睛】本题利用了角平分线定义、直角三角形中30°的角所对的直角边等于斜边的一半、勾股定理等知识.
20.(1)见解析;
(2)见解析;
(3)见解析.
【分析】(1)根据已知得出AF=AD,AB=BC=AC,∠BAC=∠DAF=60°,求出∠BAD=CAF,由SAS证△BAD≌△CAF,推出CF=BD即可.
(2)求出∠BAD=∠CAF,根据SAS证△BAD≌△CAF,推出BD=CF即可.
(3)画出图形后,根据SAS证△BAD≌△CAF,推出CF=BD即可:
【详解】解:(1)证明:∵四边形AFED是菱形,
∴AF=AD
∵△ABC是等边三角形,
∴AB=AC=BC,∠BAC=60°=∠DAF
∴∠BAC-∠DAC=∠DAF-∠DAC,即∠BAD=∠CAF
∵在△BAD和△CAF中, AB=AC,∠BAD=∠CAF,AD=AF,
∴△BAD≌△CAF(SAS)
∴CF=BD
∴CF+CD=BD+CD=BC=AC.
即①BD=CF,②AC=CF+CD.
(2)AC=CF+CD不成立,AC、CF、CD之间存在的数量关系是AC=CF-CD.理由如下:
由(1)知:AB=AC=BC,AD=AF,∠BAC=∠DAF=60°,
∴∠BAC+∠DAC=∠DAF+∠DAC,即∠BAD=∠CAF
∵在△BAD和△CAF中,AC=AB,∠BAD=∠CAF ,AD=AF,
∴△BAD≌△CAF(SAS)
∴BD=CF
∴CF-CD=BD-CD=BC=AC,即AC=CF-CD.
(3)补全图形如下,AC、CF、CD之间的数量关系为AC=CD-CF.
∵∠BAC=∠DAF=60°,
∴∠DAB=∠CAF,
∵在△BAD和△CAF中, AB=AC,∠DAB=∠CAF, AD=AF,
∴△BAD≌△CAF(SAS).
∴CF=BD.
∴CD-CF=CD-BD=BC=AC.
21.(1)4米
(2)1米
【分析】(1)根据勾股定理直接求出OA的长度即可;
(2)先求出OC的长度,然后根据勾股定理求出OD的长度,用OD-OB即可得出答案.
【详解】(1)解:∵∠AOB=90°,米,米,
∴AO==4(米),
答:梯子顶端与地面的距离OA的长为4米.
(2)解:∵(米),米,
∴OD==4(米),
∴BD=OD﹣OB=4﹣3=1(米).
【点睛】本题主要考查了勾股定理的应用,解题的关键是熟练掌握勾股定理的内容,如果一个直角三角形的两条直角边为a、b,斜边为c,那么.
22.(1)见解析
(2),理由见解析
【分析】本题考查了等腰三角形的性质、全等三角形综合问题以及勾股定理,证是解题关键.
(1)证得,结合、可得,即可求证;
(2)由得,结合,得,根据勾股定理即可求解.
【详解】(1)证明:∵,D是的中点,
∴,
∵,
∴,
∴,
由题意得:,
∴,
∴,
∴;
(2)解:,理由如下:
∵,
∴,
∵,,
∴,
∴,
∵,
∴.
23.
【分析】此题考查了勾股定理,以及三角形面积求法,熟练掌握勾股定理是解本题的关键.
用勾股定理求的长,再利用面积求,在中,用勾股定理求.
【详解】
解:在中,,
,
.
由三角形的面积公式得,
∴.
在中,,
.
.
所以的长为.
24.最长路径为A→E→D→F→B;最短路径为A→G→B,理由见解析.
【分析】利用勾股定理分别计算出三条路径的长,比较大小即可得.
【详解】第一条路径的长度为++=2+,
第二条路径的长度为++1+=+++1,
第三条路径的长度为+=2+,
∵2+<2+<+++1,
∴最长路径为A→E→D→F→B;最短路径为A→G→B.
【点睛】本题主要考查勾股定理的应用,解题的关键是根据勾股定理求得每条线段的长度.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
