19.3矩形、菱形、正方形同步练习(含解析)
文档属性
| 名称 | 19.3矩形、菱形、正方形同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
19.3矩形、菱形、正方形
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.被称为“几何之父”的古希腊数学家欧几里得,在他的几何原本中,记载了用图解法解方程的方法,类似地我们可以用折纸的方法求方程的一个正根如图,一张边长为的正方形的纸片,先折出,的中点,,再沿过点的直线折叠使落在线段上,点的对应点为点,折痕为,点在边上,连接,,则长度恰好是方程的一个正根的线段为( )
A.线段 B.线段 C.线段 D.线段
2.如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE,设AC=12,BD=16,则OE的长为( )
A.8 B.9 C.10 D.12
3.已知菱形的对角线为和,下列条件中,不能使菱形为正方形的是( )
A. B. C. D.
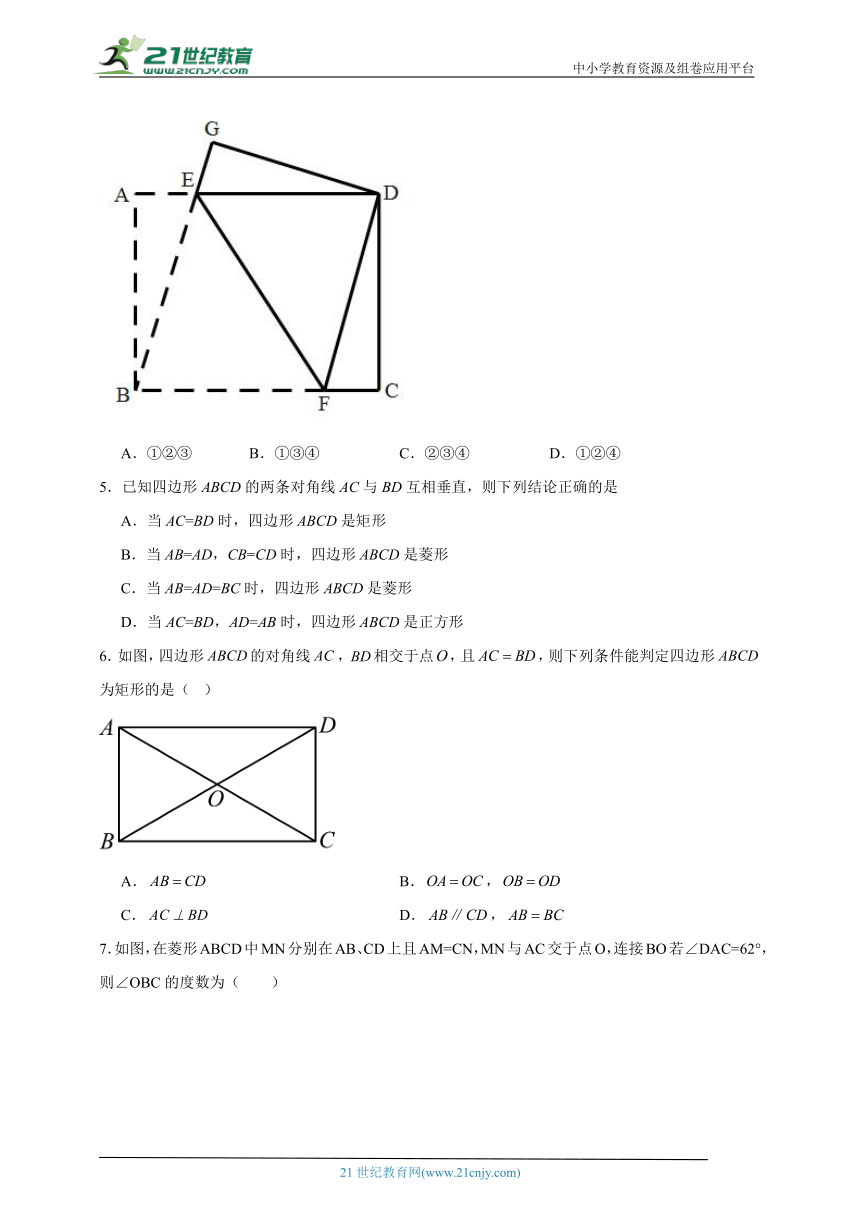
4.如图,将矩形(长方形)沿折叠,使点与点重合,点落在处,连接,,则下列结论:①,②,③,④,,三点在同一直线上,其中正确的是( )
A.①②③ B.①③④ C.②③④ D.①②④
5.已知四边形ABCD的两条对角线AC与BD互相垂直,则下列结论正确的是
A.当AC=BD时,四边形ABCD是矩形
B.当AB=AD,CB=CD时,四边形ABCD是菱形
C.当AB=AD=BC时,四边形ABCD是菱形
D.当AC=BD,AD=AB时,四边形ABCD是正方形
6.如图,四边形的对角线,相交于点,且,则下列条件能判定四边形为矩形的是( )
A. B.,
C. D.,
7.如图,在菱形ABCD中MN分别在AB、CD上且AM=CN,MN与AC交于点O,连接BO若∠DAC=62°,则∠OBC的度数为( )
A.28° B.52° C.62° D.72°
8.C、D是线段的垂直平分线上的两点,平分,则下列说法不一定正确的是( ).
A. B. C.垂直平分 D.
9.矩形的四个内角平分线围成的四边形( )
A.一定是正方形 B.是矩形
C.菱形 D.只能是平行四边形
10.下列命题:①一组对边平行且另一组对边相等的四边形是平行四边形;②一组邻角相等的平行四边形是矩形;③顺次连结矩形四边中点得到的四边形是菱形;④如果一个菱形的对角线相等,那么它一定是正方形.其中真命题个数是( )
A.个 B.个 C.个 D.个
11.矩形ABCD的面积是16,它的长与宽的比为4:1,则该矩形的宽为( )
A.1 B.2 C.3 D.4
12.如图,四边形ABCD是菱形,对角线AC,BD交于点O,E是边AD的中点,过点E作EF⊥BD,EG⊥AC,点F,G为垂足,若AC=10,BD=24,则FG的长为( )
A. B.8 C. D.
二、填空题
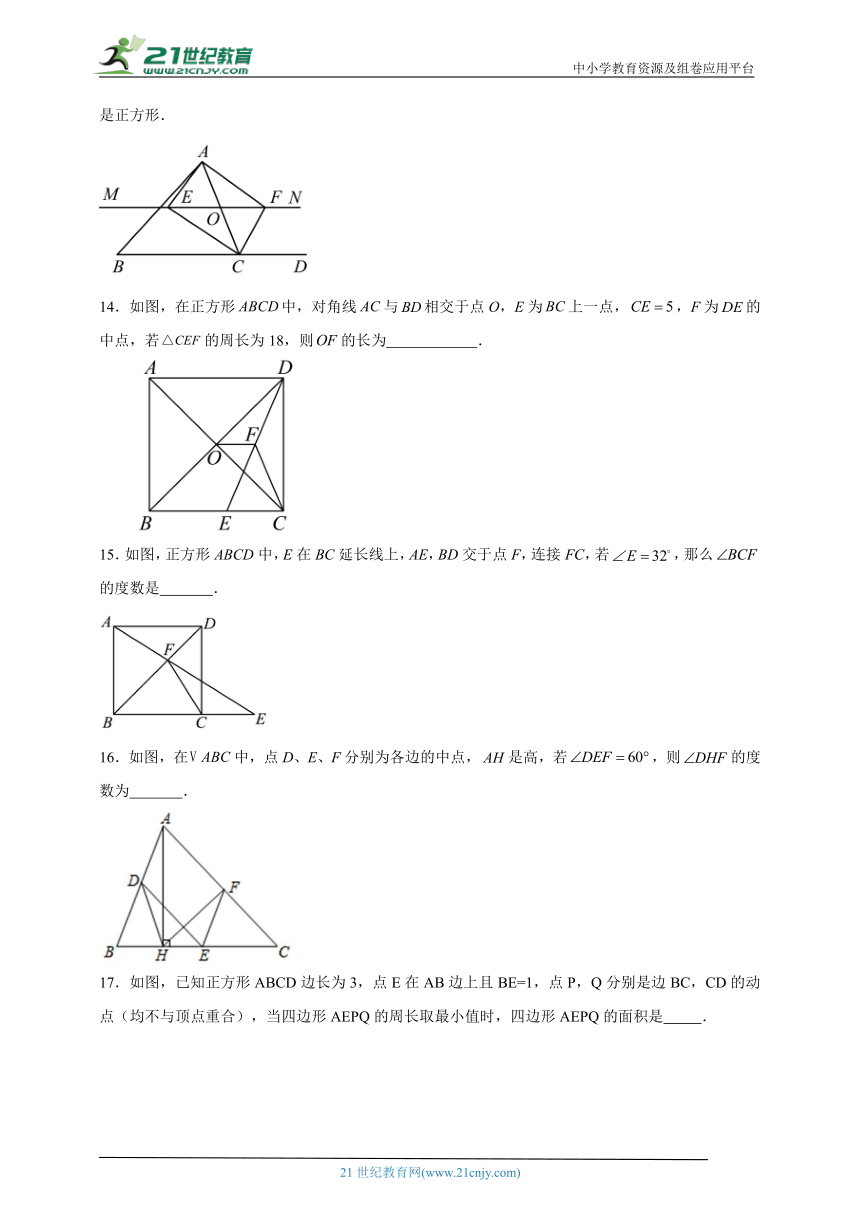
13.如图,在△ABC中,O是AC上一动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.若点O运动到AC的中点,则∠ACB= °时,四边形AECF是正方形.
14.如图,在正方形中,对角线与相交于点O,E为上一点,,F为的中点,若的周长为18,则的长为 .
15.如图,正方形ABCD中,E在BC延长线上,AE,BD交于点F,连接FC,若,那么的度数是 .
16.如图,在中,点D、E、F分别为各边的中点,是高,若,则的度数为 .
17.如图,已知正方形ABCD边长为3,点E在AB边上且BE=1,点P,Q分别是边BC,CD的动点(均不与顶点重合),当四边形AEPQ的周长取最小值时,四边形AEPQ的面积是 .
三、解答题
18.如图,在中,,的平分线交于点,DEAB,DFAC.
(1)求证:四边形为正方形;
(2)若,求四边形的面积.
19.如图,在中,分别是边的中点,是对角线,交的延长线于.
(1)求证:四边形是平行四边形;
(2)若四边形是矩形,判断四边形是怎样的特殊四边形?证明你的结论.
20.如图,正方形、、、的边长分别为2、4、6、4,四个正方形按照如图所示的方式摆放,点、、分别位于正方形、、对角线的交点,则阴影部分的面积和为.
21.给你一张正方形的彩色纸,你能一刀剪出如图所示的正方形孔吗?
22.如图,在菱形ABCD中,对角线AC,BD相交于点O,E是CD的中点,连接OE.过点C作CF//BD交OE的延长线于点F,连接DF.
求证:(1)△ODE≌△FCE;
(2)四边形OCFD是矩形.
23.如图,在边长为4的正方形ABCD中,请画出以A为一个顶点,另外两个顶点在正方形ABCD的边上,且含边长为3的所有大小不同的等腰三角形.(要求:只要画出示意图,并在所画等腰三角形长为3的边上标注数字3)
24.如图,在四边形 ABCD 中,点 E,F,G,H 分别是边 AB,BC,CD,DA 的中点,顺次连接 E,F,G,H,得到的四边形 EFGH 叫中点四边形.求证:四边形 EFGH 是平行四边形.
《19.3矩形、菱形、正方形》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B C D B C B A D A B
题号 11 12
答案 B A
1.B
【分析】设,则,从而可以用表示等式.利用正方形的面积等于图中各个三角形的面积和,列等量关系.根据方程解出正根为,再判断这个数值和题目中的哪条线段接近.
【详解】解:设,则.
由题意可知:,是的中点,
,.
∴,
,
,
.
的解为:,
取正值为.
这条线段是线段.
故选:B.
【点睛】此题考查的是一元二次方程的应用,运用勾股定理和面积法找到线段的关系是解题的关键.
2.C
【分析】先证明四边形OCED为平行四边形,再利用菱形的性质证明 求解 再证明平行四边形OCED为矩形,再利用矩形的性质可得答案.
【详解】解:∵DE∥AC,CE∥BD,
∴四边形OCED为平行四边形,
∵四边形ABCD是菱形,AC=12,BD=16,
∴AC⊥BD,
∴∠DOC=90°,
∴平行四边形OCED为矩形,
∴OE=CD=10,
故选:C.
【点睛】本题考查的是菱形的性质,矩形的判定与性质,勾股定理的应用,掌握以上知识是解题的关键.
3.D
【分析】本题考查菱形的性质及正方形的判定.在菱形基础上添加一个内角为直角或者对角线相等即可得到正方形,据此求解即可.
【详解】解:要使菱形成为正方形,只要菱形满足以下条件之一即可,(1)有一个内角是直角(2)对角线相等.
A、当时,菱形是正方形,选项不符合题意;
B、当时,菱形是正方形,选项不符合题意;
C、当时,,菱形是正方形,选项不符合题意;
D、当时,菱形不能确定是正方形,选项符合题意;
故选:D.
4.B
【分析】根据矩形的对边平行和折叠前后的图形对称的性质,逐项进行分析可得出正确结论.
【详解】∵将矩形ABCD沿EF折叠,使点B与点D重合,点A落在点G处,
∴BF=DF,∠BFE=∠EFD,
∵,
∴∠DEF=∠EFB,
∴∠DEF=∠DFE,
∴DE=DF,故①正确;
同理,∠BEF=∠DEF,∠EBF=∠AEB,
∠AEB与∠BEF不一定相等,
∴∠EBF与∠BEF不一定相等,FB与FE不一定相等,故②错误;
,
∵BF=DF,DE=DF,
∴DE=BF,
又∵,
∴四边形BFDE是平行四边形,
∴,故③正确;
由矩形可知,
已证四边形BFDE是平行四边形,则有,
∴,,三点在同一直线上,即④正确;
综上正确的有①③④,
故选:B
【点睛】本题考查了矩形的性质及折叠的性质,掌握翻折变换是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解题的关键.
5.C
【详解】
A、对角线AC与BD互相垂直,AC=BD时,无法得出四边形ABCD是矩形,故此选项错误.
B、当AB=AD,CB=CD时,无法得到四边形ABCD是菱形,故此选项错误.
C、当两条对角线AC与BD互相垂直,AB=AD=BC时,
∴BO=DO,AO=CO,
∴四边形ABCD是平行四边形.
∵两条对角线AC与BD互相垂直,
∴平行四边形ABCD是菱形,故此选项正确.
D、当AC=BD,AD=AB时,无法得到四边形ABCD是正方形,故此选项错误.
故选:C.
6.B
【分析】本题主要考查矩形的判定方法、熟练掌握矩形的判定方法是解题的关键.矩形的常用判定方法有:对角线相等的平行四边形是矩形;有一个角是90度的平行四边形是矩形;有三个角是90度的四边形是矩形.据此逐项分析判断即可.
【详解】解:A、由,无法判断四边形是矩形,故不符合题意;
B、∵,,
∴四边形是平行四边形,
∵,
∴四边形是矩形,故本选项符合题意;
C、由,无法判断四边形是矩形,故不符合题意;
D、由,,,无法判断四边形是矩形,故不符合题意.
故选:B.
7.A
【分析】连接OB,根据菱形的性质以及AM=CN,利用ASA可得△AMO≌△CNO,可得AO=CO,然后可得BO⊥AC,继而可求得∠OBC的度数.
【详解】解:连接OB,
∵四边形ABCD为菱形
∴AB∥CD,AB=BC,
∴∠MAO=∠NCO,∠AMO=∠CNO,
在△AMO和△CNO中,
∵,
∴△AMO≌△CNO(ASA),
∴AO=CO,
∵AB=BC,
∴BO⊥AC,
∴∠BOC=90°,
∵∠DAC=62°,
∴∠BCA=∠DAC=62°,
∴∠OBC=90°-62°=28°.
故选A.
【点睛】本题考查了菱形的性质和全等三角形的判定和性质,注意掌握菱形对边平行以及对角线相互垂直的性质.
8.D
【分析】根据线段垂直平分线的性质对各选项进行逐一判断即可.
【详解】解:根据题意可画出下图,
A、∵C、D是线段的垂直平分线上的两点,线段垂直平分线上的点到线段两端的距离相等,∴AD=BD,故本选项正确;
B、∵C是线段的垂直平分线上的点,∴AC=BC,∴,∵AB平分,∴,∴,∴,故本选项正确;
C、∵AB平分,∴,∵,∴,∵,∴,∴,∵,∴垂直平分,故本选项正确;
D、∵AB与CD互相垂直平分,∴四边形ABCD是菱形,∴AB、CD不一定相等,故本选项错误;
故选:D.
【点睛】本题考查了线段垂直平分线的性质,平行线的判定,全等三角形的判定和性质,菱形的判定等知识点,综合运用以上性质定理是解答此题的关键.
9.A
【详解】矩形的四个角平分线将矩形的四个角分成8个45°的角,因此形成的四边形每个角是90°.又知两条角平分线与矩形的一边构成等腰直角三角形,所以这个四边形邻边相等,根据有一组邻边相等的矩形是正方形,得到该四边形是正方形.
故选A.
点睛:本题是考查正方形的判别方法,判别一个四边形为正方形主要根据正方形的概念,方法有两种:①先说明它是矩形,再说明有一组邻边相等;②先说明它是菱形,再说明它有一个角为直角.
10.B
【分析】根据平行四边形的判定方法对①进行判断;根据矩形的判定方法对②进行判断即可;根据三角形中位线性质和菱形的判定方法对③进行判断;根据正方形的判定方法对④进行判断.
【详解】解:①错误,反例为等腰梯形;②正确,理由一组邻角相等,且根据平行四边形的性质,可得它们都为直角,从而推得矩形;③正确,理由:得到的四边形的边长都等于矩形对角线的一半;④正确.
故答案为B.
【点睛】本题考查了命题与定理:判断一件事情的语句,叫做命题.判定一个命题的真假关键在于对基本知识的掌握.
11.B
【详解】设矩形的宽为x,则长为4x.
根据题意得:4x2=16,
所以x2=4.
根据算术平方根的意义可得x=2.
故选:B.
12.A
【分析】由菱形的性质得出OA=OC=5,OB=OD=12,AC⊥BD,根据勾股定理求出AD=13,由直角三角形斜边上的中线等于斜边的一半求出OE=6.5,证出四边形EFOG是矩形,得到EO=GF即可得出答案.
【详解】解:连接OE,
∵四边形ABCD是菱形,
∴OA=OC=5,OB=OD=12,AC⊥BD,
在Rt△AOD中,AD==13,
又∵E是边AD的中点,
∴OE=AD=×13=6.5,
∵EF⊥BD,EG⊥AC,AC⊥BD,
∴∠EFO=90°,∠EGO=90°,∠GOF=90°,
∴四边形EFOG为矩形,
∴FG=OE=6.5.
故选:A.
【点睛】本题考查了菱形的性质、矩形的判定与性质、直角三角形斜边上中线定理等知识;熟练掌握菱形的性质和矩形的性质是解题的关键.
13.90
【详解】(1)∵MN∥BC,
∴∠OEC=∠ECB,∠OFC=∠FCD.
又∵CE平分∠ACB,FC平分∠ACD.
∴∠ECB=∠OCE,∠OCF=∠FCD,
∴∠OEC=∠OCE,∠OFC=∠OCF,
∴EO=OC,FO=OC,
∴EO=FO;
OE=OC=OF,
当OC=OA,即点O为AC的中点时,
∴OE=OC=OF=OA,
∴四边形AECF是平行四边形,AC=EF,
∴这时四边形AECF是矩形,
∴当点O运动到AC中点时,
四边形AECF是矩形,
由正方形AECF可知,AC⊥EF,
又∵EF∥BC,
∴∠ACB=90°,
∴△ABC是∠ACB=90°.
14./
【分析】利用斜边上的中线等于斜边的一半和的周长,求出的长,进而求出的长,勾股定理求出的长,进而求出的长,利用三角形的中位线定理,即可得解.
【详解】解:的周长为18,
.
为的中点,
.
,
,
,
,
.
四边形是正方形,
,O为的中点,
是的中位线,
.
故答案为:.
【点睛】本题考查正方形的性质,斜边上的中线,三角形的中位线定理.熟练掌握斜边上的中线等于斜边的一半,是解题的关键.
15.58°/58度
【分析】先证明△ADF≌△CDF,得到∠DAF=∠DCF,求出∠DAF,进而可求∠BCF.
【详解】解:∵在正方形ABCD,AD=CD,∠ADF=∠CDF=45°,DF=DF,
∴△ADF≌△CDF(SAS),
∴∠DAF=∠DCF,
又∵AD∥BC,∠E=32°,
∴∠DAF=32°,
∴∠DCF=32°,
∴∠BCF=∠DCB-∠DCF=90°-32°=58°.
故答案为:58°.
【点睛】本题考查的是正方形的性质,全等三角形的判定和性质,平行线的性质,掌握正方形的性质是解题的关键.
16./60度
【分析】连结,根据点D、E、F分别为各边的中点,可得,为的中位线,可确定,,利用平行线性质可得,由,点D为中点,点F为中点,根据直角三角形斜边中线性质可得,,可证在和中,即可.
【详解】解:连结,
∵点D、E、F分别为各边的中点,
∴,为的中位线,
∴,,
∴,
∵,点D为中点,点F为中点,
∴,,
在和中,
,
∴,
∴.
故答案为:.
【点睛】本题考查三角形的中位线性质,直角三角形斜边中线性质,三角形全等判定与性质,掌握三角形的中位线性质,直角三角形斜边中线性质,三角形全等判定与性质是解题关键.
17..
【详解】解:如图1所示,作E关于BC的对称点E′,点A关于DC的对称点A′,连接A′E′,四边形AEPQ的周长最小,
∵AD=A′D=3,BE=BE′=1,
∴AA′=6,AE′=4.
∵DQ∥AE′,D是AA′的中点,
∴DQ是△AA′E′的中位线,
∴DQ=AE′=2;CQ=DC﹣CQ=3﹣2=1,
∵BP∥AA′,
∴△BE′P∽△AE′A′,
∴,即,BP=,CP=BC﹣BP==,
S四边形AEPQ=S正方形ABCD﹣S△ADQ﹣S△PCQ﹣SBEP=9﹣AD DQ﹣CQ CP﹣BE BP=9﹣×3×2﹣×1×﹣×1×=,
故答案为.
【点睛】本题考查1.轴对称-最短路线问题;2.正方形的性质.
18.(1)见解析
(2)4
【分析】(1)根据题目条件可得四边形为平行四边形,进而可通过角平分线证明其邻边相等,再加上一个角,即可说明是正方形,
(2)根据正方形的性质先求出边长,即可得面积.
【详解】(1)证明:,,
四边形是平行四边形.
平分,
.
,
.
.
.
四边形是菱形.
,
四边形是正方形.
(2)解:四边形是正方形,,
,
,
,
四边形的面积为.
【点睛】本题考查平行四边形的判定与性质,正方形的判定及性质,勾股定理,熟练掌握正方形的几种判定方法及性质是解题关键.
19.(1)见解析
(2)四边形是菱形,理由见解析
【详解】(1)证明:在中,.又,
∴四边形是平行四边形.
(2)四边形是菱形.证明:∵四边形是平行四边形,.∵点分别是的中点,..∴四边形是平行四边形.∵四边形是矩形,.在中,为的中点,.∴平行四边形是菱形.
易错点分析:本题主要考查了平行四边形的性质、菱形的判定、直角三角形的性质.解题时应注意:在直角三角形中,斜边上的中线长度等于斜边长度的一半.
20.阴影部分的面积和为14
【分析】本题考查了正方形的性质,全等三角形的性质与判定,如图,因为四边形,是正方形,所以可以得到四边形是对角互补的四边形,过作,的垂线,垂足分别为,,先证,从而推得四边形的面积为正方形面积的四分之一,同样的方法,求得另外两个阴影部分面积,即可解决.
【详解】解:设正方形、、中的面积分别为,,,
如图,设与交于点,与交于点,
过分别作于,于,
连接,,
四边形是正方形,是对角线的交点,
平分,且是等腰直角三角形,
,,
,
,
四边形为正方形,
,
四边形是正方形,
,
,
在与中,
,
,
,
,
,
同理,,,
阴影部分的面积和为:.
21.能,过程见解析
【分析】根据题意,剪纸图案是正方形,为轴对称图形,根据正方形的性质,再结合轴对称性质:在平面内,如果一个图形沿一条直线对折,对折后的两部分都能完全重合,这样的图形叫做轴对称图形,这条直线就是其对称轴,即可得到答案.
【详解】解:能,具体操作如下:
首先沿着正方形的两边、中点所在直线折叠,得到矩形,如图所示:
然后沿着矩形的两边、中点所在直线折叠,得到正方形,如图所示:
最后取正方形两边、上两点、,使,沿着剪掉,即可得到图形,如图所示:
【点睛】本题考查了轴对称的意义及正方形的性质在实际生活当中的运用,熟练掌握正方形的性质及轴对称的意义是解决问题的关键.
22.(1)详见解析;(2)详见解析
【分析】(1)根据题意得出,,根据AAS即可证明;
(2)由(1)可得到,再根据菱形的性质得出,即可证明平行四边形OCFD是矩形.
【详解】证明:(1),
,.
E是CD中点,,
又
(AAS)
(2),
,.
,
四边形OCFD是平行四边形,
平行四边形ABCD是菱形,
.
平行四边形OCFD是矩形.
【点睛】此题考查矩形的判定和全等三角形的判定与性质,平行四边形的性质,解题关键在于利用全等三角形的性质进行解答.
23.作图见解析.
【分析】分类讨论如下:
①以A为圆心,以3为半径作弧,交AD、AB两点,连接即可;
②连接AC,在AC上,以A为端点,截取1.5个单位,过这个点作AC的垂线,交AD、AB两点,连接即可;
③以A为端点在AB上截取3个单位,以截取的点为圆心,以3个单位为半径画弧,交BC一个点,连接即可;
④连接AC,在AC上,以C为端点,截取1.5个单位,过这个点作AC的垂线,交BC、DC两点,然后连接A与这两个点即可;
⑤以A为端点在AB上截取3个单位,再作着个线段的垂直平分线交CD一点,连接即可.
【详解】解:满足条件的所有图形如图所示:
【点睛】本题主要考查了作图—应用与设计作图,等腰三角形的判定,勾股定理,正方形的性质,解题的关键是掌握等腰三角形的判定定理.
24.见解析
【详解】试题分析:连接BD.利用三角形中位线定理推出所得四边形对边平行且相等,故为平行四边形;
试题解析:证明:连接BD.
∵E、H分别是AB、AD的中点,
∴EH是△ABD的中位线,
EH∥BD.
同理得 FG∥BD.
∴EH=FG,EH∥FG.
∴四边形EFGH是平行四边形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
19.3矩形、菱形、正方形
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.被称为“几何之父”的古希腊数学家欧几里得,在他的几何原本中,记载了用图解法解方程的方法,类似地我们可以用折纸的方法求方程的一个正根如图,一张边长为的正方形的纸片,先折出,的中点,,再沿过点的直线折叠使落在线段上,点的对应点为点,折痕为,点在边上,连接,,则长度恰好是方程的一个正根的线段为( )
A.线段 B.线段 C.线段 D.线段
2.如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE,设AC=12,BD=16,则OE的长为( )
A.8 B.9 C.10 D.12
3.已知菱形的对角线为和,下列条件中,不能使菱形为正方形的是( )
A. B. C. D.
4.如图,将矩形(长方形)沿折叠,使点与点重合,点落在处,连接,,则下列结论:①,②,③,④,,三点在同一直线上,其中正确的是( )
A.①②③ B.①③④ C.②③④ D.①②④
5.已知四边形ABCD的两条对角线AC与BD互相垂直,则下列结论正确的是
A.当AC=BD时,四边形ABCD是矩形
B.当AB=AD,CB=CD时,四边形ABCD是菱形
C.当AB=AD=BC时,四边形ABCD是菱形
D.当AC=BD,AD=AB时,四边形ABCD是正方形
6.如图,四边形的对角线,相交于点,且,则下列条件能判定四边形为矩形的是( )
A. B.,
C. D.,
7.如图,在菱形ABCD中MN分别在AB、CD上且AM=CN,MN与AC交于点O,连接BO若∠DAC=62°,则∠OBC的度数为( )
A.28° B.52° C.62° D.72°
8.C、D是线段的垂直平分线上的两点,平分,则下列说法不一定正确的是( ).
A. B. C.垂直平分 D.
9.矩形的四个内角平分线围成的四边形( )
A.一定是正方形 B.是矩形
C.菱形 D.只能是平行四边形
10.下列命题:①一组对边平行且另一组对边相等的四边形是平行四边形;②一组邻角相等的平行四边形是矩形;③顺次连结矩形四边中点得到的四边形是菱形;④如果一个菱形的对角线相等,那么它一定是正方形.其中真命题个数是( )
A.个 B.个 C.个 D.个
11.矩形ABCD的面积是16,它的长与宽的比为4:1,则该矩形的宽为( )
A.1 B.2 C.3 D.4
12.如图,四边形ABCD是菱形,对角线AC,BD交于点O,E是边AD的中点,过点E作EF⊥BD,EG⊥AC,点F,G为垂足,若AC=10,BD=24,则FG的长为( )
A. B.8 C. D.
二、填空题
13.如图,在△ABC中,O是AC上一动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.若点O运动到AC的中点,则∠ACB= °时,四边形AECF是正方形.
14.如图,在正方形中,对角线与相交于点O,E为上一点,,F为的中点,若的周长为18,则的长为 .
15.如图,正方形ABCD中,E在BC延长线上,AE,BD交于点F,连接FC,若,那么的度数是 .
16.如图,在中,点D、E、F分别为各边的中点,是高,若,则的度数为 .
17.如图,已知正方形ABCD边长为3,点E在AB边上且BE=1,点P,Q分别是边BC,CD的动点(均不与顶点重合),当四边形AEPQ的周长取最小值时,四边形AEPQ的面积是 .
三、解答题
18.如图,在中,,的平分线交于点,DEAB,DFAC.
(1)求证:四边形为正方形;
(2)若,求四边形的面积.
19.如图,在中,分别是边的中点,是对角线,交的延长线于.
(1)求证:四边形是平行四边形;
(2)若四边形是矩形,判断四边形是怎样的特殊四边形?证明你的结论.
20.如图,正方形、、、的边长分别为2、4、6、4,四个正方形按照如图所示的方式摆放,点、、分别位于正方形、、对角线的交点,则阴影部分的面积和为.
21.给你一张正方形的彩色纸,你能一刀剪出如图所示的正方形孔吗?
22.如图,在菱形ABCD中,对角线AC,BD相交于点O,E是CD的中点,连接OE.过点C作CF//BD交OE的延长线于点F,连接DF.
求证:(1)△ODE≌△FCE;
(2)四边形OCFD是矩形.
23.如图,在边长为4的正方形ABCD中,请画出以A为一个顶点,另外两个顶点在正方形ABCD的边上,且含边长为3的所有大小不同的等腰三角形.(要求:只要画出示意图,并在所画等腰三角形长为3的边上标注数字3)
24.如图,在四边形 ABCD 中,点 E,F,G,H 分别是边 AB,BC,CD,DA 的中点,顺次连接 E,F,G,H,得到的四边形 EFGH 叫中点四边形.求证:四边形 EFGH 是平行四边形.
《19.3矩形、菱形、正方形》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B C D B C B A D A B
题号 11 12
答案 B A
1.B
【分析】设,则,从而可以用表示等式.利用正方形的面积等于图中各个三角形的面积和,列等量关系.根据方程解出正根为,再判断这个数值和题目中的哪条线段接近.
【详解】解:设,则.
由题意可知:,是的中点,
,.
∴,
,
,
.
的解为:,
取正值为.
这条线段是线段.
故选:B.
【点睛】此题考查的是一元二次方程的应用,运用勾股定理和面积法找到线段的关系是解题的关键.
2.C
【分析】先证明四边形OCED为平行四边形,再利用菱形的性质证明 求解 再证明平行四边形OCED为矩形,再利用矩形的性质可得答案.
【详解】解:∵DE∥AC,CE∥BD,
∴四边形OCED为平行四边形,
∵四边形ABCD是菱形,AC=12,BD=16,
∴AC⊥BD,
∴∠DOC=90°,
∴平行四边形OCED为矩形,
∴OE=CD=10,
故选:C.
【点睛】本题考查的是菱形的性质,矩形的判定与性质,勾股定理的应用,掌握以上知识是解题的关键.
3.D
【分析】本题考查菱形的性质及正方形的判定.在菱形基础上添加一个内角为直角或者对角线相等即可得到正方形,据此求解即可.
【详解】解:要使菱形成为正方形,只要菱形满足以下条件之一即可,(1)有一个内角是直角(2)对角线相等.
A、当时,菱形是正方形,选项不符合题意;
B、当时,菱形是正方形,选项不符合题意;
C、当时,,菱形是正方形,选项不符合题意;
D、当时,菱形不能确定是正方形,选项符合题意;
故选:D.
4.B
【分析】根据矩形的对边平行和折叠前后的图形对称的性质,逐项进行分析可得出正确结论.
【详解】∵将矩形ABCD沿EF折叠,使点B与点D重合,点A落在点G处,
∴BF=DF,∠BFE=∠EFD,
∵,
∴∠DEF=∠EFB,
∴∠DEF=∠DFE,
∴DE=DF,故①正确;
同理,∠BEF=∠DEF,∠EBF=∠AEB,
∠AEB与∠BEF不一定相等,
∴∠EBF与∠BEF不一定相等,FB与FE不一定相等,故②错误;
,
∵BF=DF,DE=DF,
∴DE=BF,
又∵,
∴四边形BFDE是平行四边形,
∴,故③正确;
由矩形可知,
已证四边形BFDE是平行四边形,则有,
∴,,三点在同一直线上,即④正确;
综上正确的有①③④,
故选:B
【点睛】本题考查了矩形的性质及折叠的性质,掌握翻折变换是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解题的关键.
5.C
【详解】
A、对角线AC与BD互相垂直,AC=BD时,无法得出四边形ABCD是矩形,故此选项错误.
B、当AB=AD,CB=CD时,无法得到四边形ABCD是菱形,故此选项错误.
C、当两条对角线AC与BD互相垂直,AB=AD=BC时,
∴BO=DO,AO=CO,
∴四边形ABCD是平行四边形.
∵两条对角线AC与BD互相垂直,
∴平行四边形ABCD是菱形,故此选项正确.
D、当AC=BD,AD=AB时,无法得到四边形ABCD是正方形,故此选项错误.
故选:C.
6.B
【分析】本题主要考查矩形的判定方法、熟练掌握矩形的判定方法是解题的关键.矩形的常用判定方法有:对角线相等的平行四边形是矩形;有一个角是90度的平行四边形是矩形;有三个角是90度的四边形是矩形.据此逐项分析判断即可.
【详解】解:A、由,无法判断四边形是矩形,故不符合题意;
B、∵,,
∴四边形是平行四边形,
∵,
∴四边形是矩形,故本选项符合题意;
C、由,无法判断四边形是矩形,故不符合题意;
D、由,,,无法判断四边形是矩形,故不符合题意.
故选:B.
7.A
【分析】连接OB,根据菱形的性质以及AM=CN,利用ASA可得△AMO≌△CNO,可得AO=CO,然后可得BO⊥AC,继而可求得∠OBC的度数.
【详解】解:连接OB,
∵四边形ABCD为菱形
∴AB∥CD,AB=BC,
∴∠MAO=∠NCO,∠AMO=∠CNO,
在△AMO和△CNO中,
∵,
∴△AMO≌△CNO(ASA),
∴AO=CO,
∵AB=BC,
∴BO⊥AC,
∴∠BOC=90°,
∵∠DAC=62°,
∴∠BCA=∠DAC=62°,
∴∠OBC=90°-62°=28°.
故选A.
【点睛】本题考查了菱形的性质和全等三角形的判定和性质,注意掌握菱形对边平行以及对角线相互垂直的性质.
8.D
【分析】根据线段垂直平分线的性质对各选项进行逐一判断即可.
【详解】解:根据题意可画出下图,
A、∵C、D是线段的垂直平分线上的两点,线段垂直平分线上的点到线段两端的距离相等,∴AD=BD,故本选项正确;
B、∵C是线段的垂直平分线上的点,∴AC=BC,∴,∵AB平分,∴,∴,∴,故本选项正确;
C、∵AB平分,∴,∵,∴,∵,∴,∴,∵,∴垂直平分,故本选项正确;
D、∵AB与CD互相垂直平分,∴四边形ABCD是菱形,∴AB、CD不一定相等,故本选项错误;
故选:D.
【点睛】本题考查了线段垂直平分线的性质,平行线的判定,全等三角形的判定和性质,菱形的判定等知识点,综合运用以上性质定理是解答此题的关键.
9.A
【详解】矩形的四个角平分线将矩形的四个角分成8个45°的角,因此形成的四边形每个角是90°.又知两条角平分线与矩形的一边构成等腰直角三角形,所以这个四边形邻边相等,根据有一组邻边相等的矩形是正方形,得到该四边形是正方形.
故选A.
点睛:本题是考查正方形的判别方法,判别一个四边形为正方形主要根据正方形的概念,方法有两种:①先说明它是矩形,再说明有一组邻边相等;②先说明它是菱形,再说明它有一个角为直角.
10.B
【分析】根据平行四边形的判定方法对①进行判断;根据矩形的判定方法对②进行判断即可;根据三角形中位线性质和菱形的判定方法对③进行判断;根据正方形的判定方法对④进行判断.
【详解】解:①错误,反例为等腰梯形;②正确,理由一组邻角相等,且根据平行四边形的性质,可得它们都为直角,从而推得矩形;③正确,理由:得到的四边形的边长都等于矩形对角线的一半;④正确.
故答案为B.
【点睛】本题考查了命题与定理:判断一件事情的语句,叫做命题.判定一个命题的真假关键在于对基本知识的掌握.
11.B
【详解】设矩形的宽为x,则长为4x.
根据题意得:4x2=16,
所以x2=4.
根据算术平方根的意义可得x=2.
故选:B.
12.A
【分析】由菱形的性质得出OA=OC=5,OB=OD=12,AC⊥BD,根据勾股定理求出AD=13,由直角三角形斜边上的中线等于斜边的一半求出OE=6.5,证出四边形EFOG是矩形,得到EO=GF即可得出答案.
【详解】解:连接OE,
∵四边形ABCD是菱形,
∴OA=OC=5,OB=OD=12,AC⊥BD,
在Rt△AOD中,AD==13,
又∵E是边AD的中点,
∴OE=AD=×13=6.5,
∵EF⊥BD,EG⊥AC,AC⊥BD,
∴∠EFO=90°,∠EGO=90°,∠GOF=90°,
∴四边形EFOG为矩形,
∴FG=OE=6.5.
故选:A.
【点睛】本题考查了菱形的性质、矩形的判定与性质、直角三角形斜边上中线定理等知识;熟练掌握菱形的性质和矩形的性质是解题的关键.
13.90
【详解】(1)∵MN∥BC,
∴∠OEC=∠ECB,∠OFC=∠FCD.
又∵CE平分∠ACB,FC平分∠ACD.
∴∠ECB=∠OCE,∠OCF=∠FCD,
∴∠OEC=∠OCE,∠OFC=∠OCF,
∴EO=OC,FO=OC,
∴EO=FO;
OE=OC=OF,
当OC=OA,即点O为AC的中点时,
∴OE=OC=OF=OA,
∴四边形AECF是平行四边形,AC=EF,
∴这时四边形AECF是矩形,
∴当点O运动到AC中点时,
四边形AECF是矩形,
由正方形AECF可知,AC⊥EF,
又∵EF∥BC,
∴∠ACB=90°,
∴△ABC是∠ACB=90°.
14./
【分析】利用斜边上的中线等于斜边的一半和的周长,求出的长,进而求出的长,勾股定理求出的长,进而求出的长,利用三角形的中位线定理,即可得解.
【详解】解:的周长为18,
.
为的中点,
.
,
,
,
,
.
四边形是正方形,
,O为的中点,
是的中位线,
.
故答案为:.
【点睛】本题考查正方形的性质,斜边上的中线,三角形的中位线定理.熟练掌握斜边上的中线等于斜边的一半,是解题的关键.
15.58°/58度
【分析】先证明△ADF≌△CDF,得到∠DAF=∠DCF,求出∠DAF,进而可求∠BCF.
【详解】解:∵在正方形ABCD,AD=CD,∠ADF=∠CDF=45°,DF=DF,
∴△ADF≌△CDF(SAS),
∴∠DAF=∠DCF,
又∵AD∥BC,∠E=32°,
∴∠DAF=32°,
∴∠DCF=32°,
∴∠BCF=∠DCB-∠DCF=90°-32°=58°.
故答案为:58°.
【点睛】本题考查的是正方形的性质,全等三角形的判定和性质,平行线的性质,掌握正方形的性质是解题的关键.
16./60度
【分析】连结,根据点D、E、F分别为各边的中点,可得,为的中位线,可确定,,利用平行线性质可得,由,点D为中点,点F为中点,根据直角三角形斜边中线性质可得,,可证在和中,即可.
【详解】解:连结,
∵点D、E、F分别为各边的中点,
∴,为的中位线,
∴,,
∴,
∵,点D为中点,点F为中点,
∴,,
在和中,
,
∴,
∴.
故答案为:.
【点睛】本题考查三角形的中位线性质,直角三角形斜边中线性质,三角形全等判定与性质,掌握三角形的中位线性质,直角三角形斜边中线性质,三角形全等判定与性质是解题关键.
17..
【详解】解:如图1所示,作E关于BC的对称点E′,点A关于DC的对称点A′,连接A′E′,四边形AEPQ的周长最小,
∵AD=A′D=3,BE=BE′=1,
∴AA′=6,AE′=4.
∵DQ∥AE′,D是AA′的中点,
∴DQ是△AA′E′的中位线,
∴DQ=AE′=2;CQ=DC﹣CQ=3﹣2=1,
∵BP∥AA′,
∴△BE′P∽△AE′A′,
∴,即,BP=,CP=BC﹣BP==,
S四边形AEPQ=S正方形ABCD﹣S△ADQ﹣S△PCQ﹣SBEP=9﹣AD DQ﹣CQ CP﹣BE BP=9﹣×3×2﹣×1×﹣×1×=,
故答案为.
【点睛】本题考查1.轴对称-最短路线问题;2.正方形的性质.
18.(1)见解析
(2)4
【分析】(1)根据题目条件可得四边形为平行四边形,进而可通过角平分线证明其邻边相等,再加上一个角,即可说明是正方形,
(2)根据正方形的性质先求出边长,即可得面积.
【详解】(1)证明:,,
四边形是平行四边形.
平分,
.
,
.
.
.
四边形是菱形.
,
四边形是正方形.
(2)解:四边形是正方形,,
,
,
,
四边形的面积为.
【点睛】本题考查平行四边形的判定与性质,正方形的判定及性质,勾股定理,熟练掌握正方形的几种判定方法及性质是解题关键.
19.(1)见解析
(2)四边形是菱形,理由见解析
【详解】(1)证明:在中,.又,
∴四边形是平行四边形.
(2)四边形是菱形.证明:∵四边形是平行四边形,.∵点分别是的中点,..∴四边形是平行四边形.∵四边形是矩形,.在中,为的中点,.∴平行四边形是菱形.
易错点分析:本题主要考查了平行四边形的性质、菱形的判定、直角三角形的性质.解题时应注意:在直角三角形中,斜边上的中线长度等于斜边长度的一半.
20.阴影部分的面积和为14
【分析】本题考查了正方形的性质,全等三角形的性质与判定,如图,因为四边形,是正方形,所以可以得到四边形是对角互补的四边形,过作,的垂线,垂足分别为,,先证,从而推得四边形的面积为正方形面积的四分之一,同样的方法,求得另外两个阴影部分面积,即可解决.
【详解】解:设正方形、、中的面积分别为,,,
如图,设与交于点,与交于点,
过分别作于,于,
连接,,
四边形是正方形,是对角线的交点,
平分,且是等腰直角三角形,
,,
,
,
四边形为正方形,
,
四边形是正方形,
,
,
在与中,
,
,
,
,
,
同理,,,
阴影部分的面积和为:.
21.能,过程见解析
【分析】根据题意,剪纸图案是正方形,为轴对称图形,根据正方形的性质,再结合轴对称性质:在平面内,如果一个图形沿一条直线对折,对折后的两部分都能完全重合,这样的图形叫做轴对称图形,这条直线就是其对称轴,即可得到答案.
【详解】解:能,具体操作如下:
首先沿着正方形的两边、中点所在直线折叠,得到矩形,如图所示:
然后沿着矩形的两边、中点所在直线折叠,得到正方形,如图所示:
最后取正方形两边、上两点、,使,沿着剪掉,即可得到图形,如图所示:
【点睛】本题考查了轴对称的意义及正方形的性质在实际生活当中的运用,熟练掌握正方形的性质及轴对称的意义是解决问题的关键.
22.(1)详见解析;(2)详见解析
【分析】(1)根据题意得出,,根据AAS即可证明;
(2)由(1)可得到,再根据菱形的性质得出,即可证明平行四边形OCFD是矩形.
【详解】证明:(1),
,.
E是CD中点,,
又
(AAS)
(2),
,.
,
四边形OCFD是平行四边形,
平行四边形ABCD是菱形,
.
平行四边形OCFD是矩形.
【点睛】此题考查矩形的判定和全等三角形的判定与性质,平行四边形的性质,解题关键在于利用全等三角形的性质进行解答.
23.作图见解析.
【分析】分类讨论如下:
①以A为圆心,以3为半径作弧,交AD、AB两点,连接即可;
②连接AC,在AC上,以A为端点,截取1.5个单位,过这个点作AC的垂线,交AD、AB两点,连接即可;
③以A为端点在AB上截取3个单位,以截取的点为圆心,以3个单位为半径画弧,交BC一个点,连接即可;
④连接AC,在AC上,以C为端点,截取1.5个单位,过这个点作AC的垂线,交BC、DC两点,然后连接A与这两个点即可;
⑤以A为端点在AB上截取3个单位,再作着个线段的垂直平分线交CD一点,连接即可.
【详解】解:满足条件的所有图形如图所示:
【点睛】本题主要考查了作图—应用与设计作图,等腰三角形的判定,勾股定理,正方形的性质,解题的关键是掌握等腰三角形的判定定理.
24.见解析
【详解】试题分析:连接BD.利用三角形中位线定理推出所得四边形对边平行且相等,故为平行四边形;
试题解析:证明:连接BD.
∵E、H分别是AB、AD的中点,
∴EH是△ABD的中位线,
EH∥BD.
同理得 FG∥BD.
∴EH=FG,EH∥FG.
∴四边形EFGH是平行四边形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
